Хаос и червоточины в модели Сачдева-Е-Китаева

Автор: Денис Аветисян

Новое исследование раскрывает связь между статистическими свойствами квантовых операторов и потенциальным возникновением геометрии пространства-времени в рамках модели SYK.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал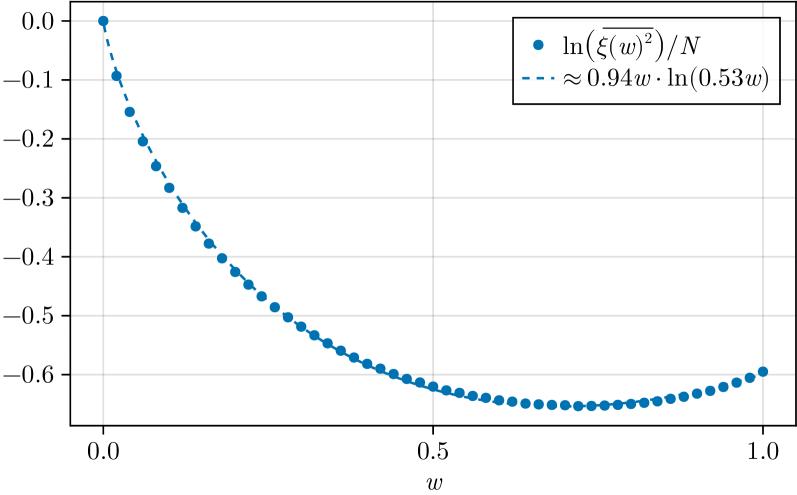

Данные SYK, проанализированные для моментов <span class="katex-eq" data-katex-display="false">\ln(\overline{\xi(w)^{2}})/N</span> при <span class="katex-eq" data-katex-display="false">q=4</span>, <span class="katex-eq" data-katex-display="false">\beta=20</span> и <span class="katex-eq" data-katex-display="false">L=1000</span>, демонстрируют соответствие с предсказаниями классического действия модели червоточины, описываемого функцией <span class="katex-eq" data-katex-display="false">c\_{1}w\ln(c\_{2}w)</span>, где наилучшее соответствие достигается при значениях <span class="katex-eq" data-katex-display="false">c\_{1}\approx 0.94</span> и <span class="katex-eq" data-katex-display="false">c\_{2}\approx 0.53</span>. — Данные SYK, проанализированные для моментов $\ln(\overline{\xi(w)^{2}})/N$ при $q=4$ , $\beta=20$ и $L=1000$ , демонстрируют соответствие с предсказаниями классического действия модели червоточины, описываемого функцией $c\_{1}w\ln(c\_{2}w)$ , где наилучшее соответствие достигается при значениях $c\_{1}\approx 0.94$ и $c\_{2}\approx 0.53$ .

Работа посвящена изучению тепловых одноточечных функций в модели Сачдева-Е-Китаева с использованием симметрии реплик и уравнений Швингера-Дисона, что позволяет исследовать ее связь с голографической дуальностью и квантовой гравитацией.

Несмотря на кажущуюся оторванность квантовой информации от геометрии пространства-времени, последние исследования указывают на глубокую связь между этими областями. В работе ‘Magic and Wormholes in the Sachdev-Ye-Kitaev Model’ исследуются статистические свойства корреляторов в модели Сачва-Йе-Китайэва (SYK), демонстрируя, что хаотичные системы описываются случайными величинами, связанными с геометрией червоточин. Полученные результаты позволяют установить количественную связь между случайностью операторов, дуальностью AdS/CFT и возникновением геометрии, подобной замкнутым вселенным. Каким образом эти связи могут пролить свет на природу квантовой гравитации и структуру пространства-времени на самых фундаментальных уровнях?

От Простоты к Сложности: Модель SYK как Отправная Точка

Многочастичные квантовые системы, такие как модель SYK, демонстрируют сложное эмерджентное поведение, которое существенно затрудняет применение традиционных аналитических методов. В отличие от систем с небольшим числом частиц, где можно точно рассчитать все свойства, в этих системах взаимодействие между частицами приводит к появлению коллективных явлений, которые невозможно предсказать, исходя из свойств отдельных частиц. Это обусловлено экспоненциальным ростом сложности при увеличении числа частиц и необходимостью учитывать корреляции между ними. Модель SYK, будучи сравнительно простым примером, служит важной отправной точкой для изучения подобных систем, позволяя исследовать фундаментальные вопросы о природе сложности и эмерджентности в квантовой механике и, потенциально, устанавливать связи между физикой конденсированного состояния и квантовой гравитацией.

Для адекватного описания поведения сложных квантовых систем, характеризующихся сильными взаимодействиями, традиционных мер корреляции и запутанности оказывается недостаточно. Простое вычисление корреляционных функций или энтропии запутанности не способно полностью отразить всю сложность возникающих явлений. Требуются новые инструменты и подходы, позволяющие характеризовать более тонкие формы запутанности и корреляций, такие как многочастичная запутанность или нелокальные корреляции. Изучение статистических моментов операторов, как показано на примере модели SYK, предоставляет один из перспективных путей для раскрытия скрытой структуры этих систем и понимания их коллективного поведения, выходящего за рамки описания с помощью отдельных частиц или простых корреляций. Это открывает возможности для разработки более точных и эффективных методов анализа, позволяющих предсказывать и контролировать свойства сложных квантовых материалов и устройств.

Модель SYK представляет собой уникальную платформу для исследования сложных задач, возникающих при изучении многих тел квантовых систем, объединяя принципы конденсированной среды и квантовой гравитации. В отличие от традиционных моделей, SYK демонстрирует богатое поведение, сохраняя при этом математическую доступность для анализа. Этот компромисс позволяет исследователям исследовать сложные взаимосвязи между различными физическими явлениями, от свойств экзотических материалов до структуры пространства-времени на самых фундаментальных уровнях. Благодаря своей структуре, модель SYK позволяет исследовать явления, связанные с сильной корреляцией и квантовой запутанностью, что делает ее ценным инструментом для понимания нетривиальных состояний материи и природы черных дыр.

Исследование статистических моментов операторов в модели SYK имеет ключевое значение для понимания её сложного поведения. Данная работа демонстрирует, что начиная с четвертого момента (q ≥ 4), эти моменты демонстрируют гауссову структуру. Это означает, что флуктуации операторов становятся предсказуемыми и описываются нормальным распределением, что существенно упрощает анализ системы. Выявление гауссовости для высоких моментов позволяет исследователям применять известные математические методы для изучения корреляций и запутанности в модели SYK, открывая путь к более глубокому пониманию её связи с такими областями, как квантовая гравитация и физика конденсированного состояния. $q$ обозначает порядок статистического момента, а обнаруженная гауссовость указывает на фундаментальное свойство системы, ограничивающее ее хаотичность и позволяющее строить более точные теоретические модели.

Предлагаемая модель связывает ансамблевое среднее функции разделения SYK с гравитальным интегралом по траекториям, включающим различные геометрии и топологии, при этом для описания корреляций граничных фермионных операторов используется геодезическое приближение, а учет топологических особенностей, таких как геометрия в виде червоточины, необходим для объяснения дисперсии случайных тепловых одноточечных функций.

Уравнения Швингера-Дисона: Приближая Сложность

Уравнения Швингера-Дисона представляют собой мощный непертурбативный подход к получению приближенных решений в квантовой теории поля. В отличие от традиционных методов теории возмущений, которые полагаются на разложение в ряд по малому параметру, эти уравнения позволяют исследовать системы, где такие разложения неприменимы или сходятся медленно. Они основаны на функциональных уравнениях для корреляционных функций, таких как $G(x)$ , описывающих распространение частиц, и позволяют самосогласованно учитывать взаимодействия между ними. Решение уравнений Швингера-Дисона, как правило, требует численных методов или приближений, однако они предоставляют информацию о непертурбативной структуре теории, включая свойства вакуума и возбужденных состояний, недоступные при использовании стандартных методов.

Применение уравнений Швингера-Дисона к модели SYK требует использования функций Грина для описания распространения частиц. Функции Грина, представляющие собой корреляционные функции одночастичных операторов, позволяют учитывать взаимодействия между частицами и описывать их динамику в рамках невозмутительной теории. В контексте SYK-модели, функции Грина используются для описания распространения майорановских фермионов, составляющих основу системы. Расчет этих функций позволяет определить энергетические спектры и другие физические свойства модели, а также исследовать ее фазовые переходы и критическое поведение. $G(x,t) = \langle \psi(x,t) \psi^\dagger(0,0) \rangle$ является типичным примером функции Грина, описывающей распространение фермиона.

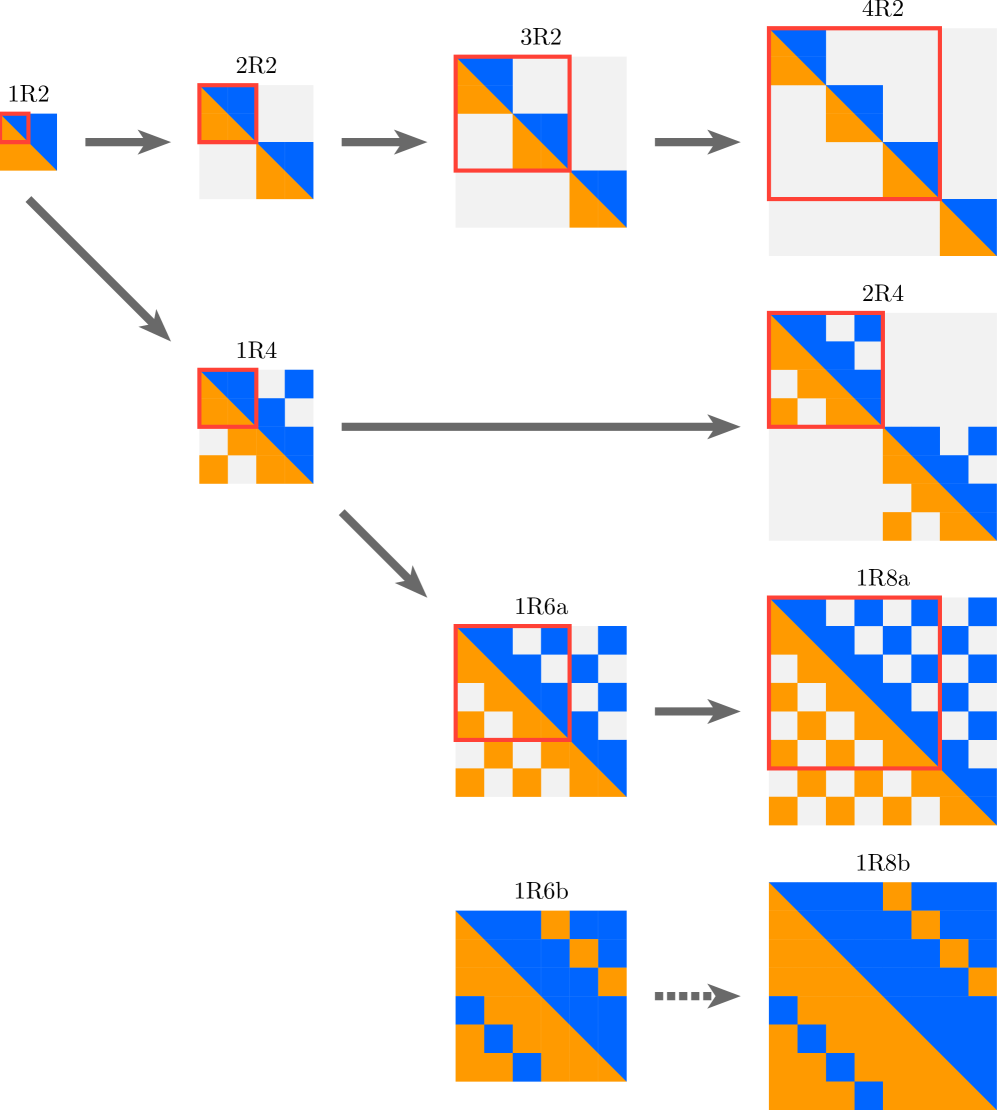
Для упрощения анализа сложной модели SYK используется метод репликационной симметрии, заключающийся в рассмотрении множества идентичных копий исходной системы. Вместо анализа одной системы с $N$ взаимодействующими фермионами, вычисляются корреляционные функции для $n$ реплик, где $n$ — целое число. Этот подход позволяет свести задачу вычисления сложных функциональных интегралов к более управляемым выражениям, поскольку усреднение по репликам эффективно упрощает структуру корреляционных функций. Репликационная симметрия предполагает, что все реплики эквивалентны, что существенно снижает вычислительную сложность, хотя и требует аккуратного обращения с возможными нарушениями симметрии при более детальном анализе.

В реализации антициркулянтной репликационной структуры для упрощения вычислений вводятся антипериодические граничные условия. Этот подход позволяет рассчитать дисперсию ожидаемых значений Майорановских строк, которая определяется как $e^{-2N\phi(w)}$ , где $N$ — число Майорановских фермионов, а $\phi(w)$ — функция, зависящая от частоты $w$ . Наложение антипериодических условий существенно снижает вычислительную сложность при решении уравнений Швингера-Дисона для модели SYK, обеспечивая возможность анализа флуктуаций в корреляциях Майорановских операторов.

Матричные тепловые карты различных (недиагональных) реплик (R=2,4,6,8) демонстрируют инвариантность по отношению к уравнениям Швингера-Дайсона и наличие «хорошо обусловленных» седловых точек для всех $q$ и β, при этом оранжевый цвет соответствует значению +1/2, синий -1/2, а серый — 0, а стрелки указывают на отношения самоподобия между репликами разных размеров.

Количественная Оценка Запутанности: Чистота, Энтропия Рени и «Магия»

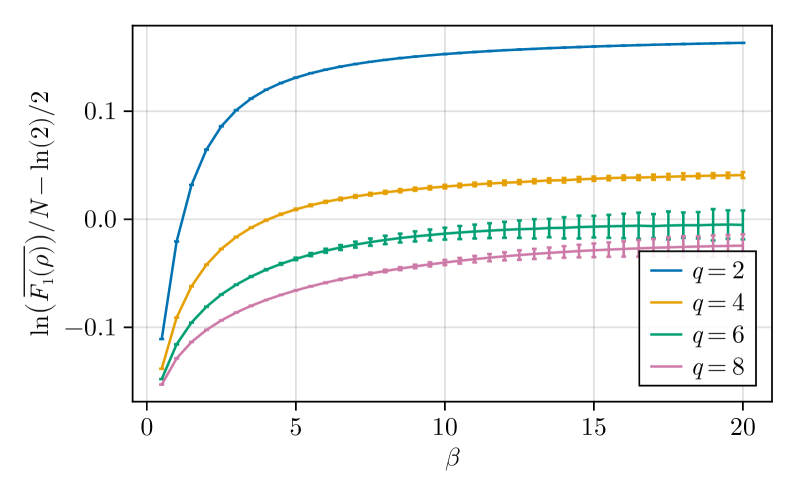
В контексте модели SYK, чистота (Purity) выступает ключевой метрикой для количественной оценки смешанности квантовых состояний. Чистота, определяемая как $Tr(\rho^2)$ , где ρ — матрица плотности, позволяет оценить степень запутанности системы. Значение чистоты, близкое к единице, указывает на чистое состояние, в то время как значения, стремящиеся к нулю, соответствуют полностью смешанному состоянию. В модели SYK наблюдается значительное отклонение от классических состояний, что подтверждается низкими значениями чистоты, указывающими на высокую степень квантовой запутанности и сложную структуру корреляций между кубитами.

Второй Рени энтропия, основанная на понятии чистоты $P = Tr(\rho^2)$ , предоставляет более точную характеристику запутанности, чем сама чистота. В то время как чистота указывает на общую смешанность квантового состояния ρ, Второй Рени энтропия, определяемая как $S_2 = -log_2(P)$ , позволяет количественно оценить степень запутанности, измеряя отклонение состояния от полностью смешанного. Более высокая величина Второй Рени энтропии соответствует большему уровню запутанности и, следовательно, большему объему квантовой информации, заключенной в состоянии. Этот показатель особенно полезен для анализа систем, где классические корреляции не могут полностью описать наблюдаемое поведение.

Стабилизаторная энтропия Рени $S_2$ количественно определяет степень нестабилизаторности квантовой системы. Нестабилизаторные состояния — это состояния, которые невозможно представить как суперпозицию стабилизаторных состояний, и характеризуют наличие неклассических ресурсов, обозначаемых как ‘магия’. Высокое значение стабилизаторной энтропии Рени указывает на значительное количество неклассических корреляций и, следовательно, на потенциальную возможность достижения квантового преимущества в вычислительных задачах. Данная метрика позволяет оценить степень отклонения системы от классического поведения, измеряя количество ресурсов, необходимых для ее эффективной симуляции на классическом компьютере.

Использование метрик, таких как чистота и энтропия Рени, позволяет количественно оценить отклонение модели SYK от классического поведения и определить наличие квантового преимущества. Расчеты второй энтропии Рени $S_2$ демонстрируют соответствие между прямым вычислением и максимизацией по седловым точкам, что подтверждает надежность метода оценки степени запутанности и неклассичности системы. Согласованность этих подходов указывает на то, что модель SYK действительно обладает характеристиками, недоступными для классического моделирования, что делает ее перспективной для изучения квантовых явлений и разработки квантовых алгоритмов.

Зависимость логарифма устойчивости нижней границы от обратной температуры при <span class="katex-eq" data-katex-display="false">q=2</span>-8 демонстрирует, что неопределенность, оцениваемая по отклонениям второй энтропии Рени, показанной на рисунке 14, влияет на точность определения устойчивости. — Зависимость логарифма устойчивости нижней границы от обратной температуры при $q=2$ -8 демонстрирует, что неопределенность, оцениваемая по отклонениям второй энтропии Рени, показанной на рисунке 14, влияет на точность определения устойчивости.

От Квантовой Системы к Гравитации: Джексона-Тейтельбойма и Червоточины

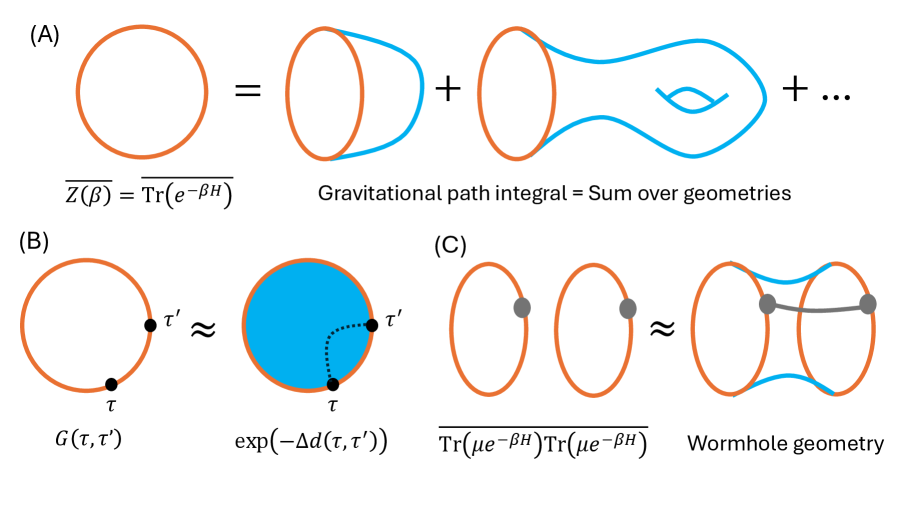
Теория гравитации Джексона-Тейтельбойма предоставляет уникальный инструмент для моделирования так называемого “bulk dual” — объемного соответствия — к модели SYK. Эта теория, являясь упрощенной версией общей теории относительности, позволяет исследовать сложные квантовые системы, такие как SYK, через призму гравитации. В частности, она оперирует с двумерной гравитацией, что значительно упрощает вычисления, сохраняя при этом ключевые характеристики, необходимые для установления связи с квантовой системой. Использование теории Джексона-Тейтельбойма позволяет перейти от описания квантовых корреляций в SYK-модели к геометрическим свойствам пространства-времени в “bulk”, открывая перспективы для понимания взаимосвязи между квантовой механикой и гравитацией. Данный подход демонстрирует, что свойства SYK-модели могут быть интерпретированы как геометрические характеристики соответствующего гравитационного пространства, что является важным шагом в построении теории квантовой гравитации.

В рамках теории Якива-Тейтельбойма, взаимосвязь между запутанностью в модели SYK и геометрией пространства-времени проявляется в виде геометрии червоточин. Запутанность между степенями свободы модели SYK, что является мерой корреляций между ними, не рассматривается как абстрактное понятие, а напрямую кодируется в геометрии так называемых червоточин — гипотетических туннелей, соединяющих различные точки пространства-времени. Чем сильнее запутанность между двумя областями модели SYK, тем «ближе» они оказываются в этой геометрической интерпретации, соединенные короткой «горловиной» червоточины. Данная концепция предлагает радикально новый взгляд на природу пространства-времени, предполагая, что оно возникает не как нечто фундаментальное, а как эмерджентное свойство квантовой запутанности, и что понимание структуры запутанности может привести к пониманию структуры самой Вселенной. $Δℑ_{rel}$ играет ключевую роль в описании этой взаимосвязи.

Теория Шварцшиана представляет собой эффективное описание динамики границы рассматриваемого объемного пространства-времени. Она позволяет упростить анализ сложных гравитационных систем, фокусируясь на поведении на границе, что особенно полезно при исследовании соответствия между квантовыми системами, такими как модель SYK, и геометрией пространства-времени. Эта теория описывает динамику границы с помощью $Sch(G)$ — алгебры Шварцшиана, что позволяет выразить сложные гравитационные эффекты через более простые математические объекты. Использование теории Шварцшиана позволяет получить количественное согласие между результатами, полученными на границе (в рамках модели SYK), и гравитационными вычислениями при больших значениях β, что подтверждает глубокую связь между квантовой запутанностью и геометрией пространства-времени.

Исследования в области теории гравитации Джексона-Тейтельбойма указывают на фундаментальную связь между квантовой запутанностью и возникновением самой структуры пространства-времени. Предполагается, что запутанность — это не просто корреляция между частицами, а ключевой ингредиент, формирующий геометрию, которую мы воспринимаем как пространство-время. Количественное согласие между результатами, полученными на границе системы SYK, и расчетами в гравитационной модели при больших значениях β, подтверждает эту гипотезу. Более того, продемонстрированная отрицательная и уменьшающаяся величина $Δℑ_{rel}$ с увеличением $L$ при $q=4$ указывает на то, что степень запутанности напрямую связана с геометрическими характеристиками пространства-времени, открывая новые перспективы в понимании квантовой гравитации и природы реальности.

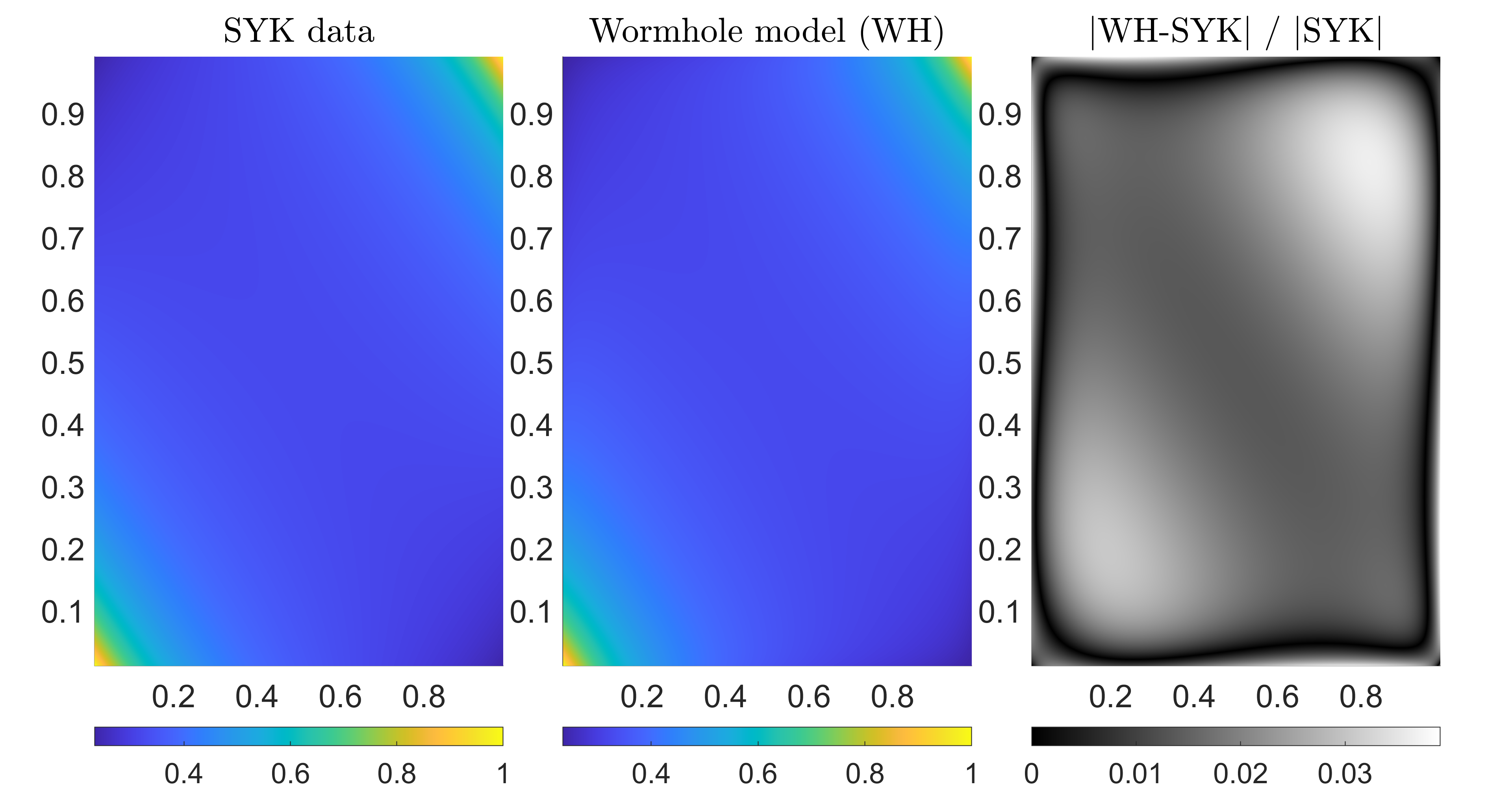
Анализ функции <span class="katex-eq" data-katex-display="false">G_{21}( au, au')</span> для параметров SYK (<span class="katex-eq" data-katex-display="false">eta = 20</span>, <span class="katex-eq" data-katex-display="false">w = 0.25</span>, <span class="katex-eq" data-katex-display="false">L = 2000</span>) показал соответствие между нормализованной функцией и предсказанием о существовании червоточин с отклонением не более 4%, что подтверждается параметрами подгонки <span class="katex-eq" data-katex-display="false">b = 6.5</span> и <span class="katex-eq" data-katex-display="false">f = 0.33</span>. — Анализ функции $G_{21}( au, au')$ для параметров SYK ( $eta = 20$ , $w = 0.25$ , $L = 2000$ ) показал соответствие между нормализованной функцией и предсказанием о существовании червоточин с отклонением не более 4%, что подтверждается параметрами подгонки $b = 6.5$ и $f = 0.33$ .

Исследование статистических свойств одноточечных функций в модели SYK, представленное в работе, стремится к упрощению сложного, выделяя ключевые связи между случайностью операторов и возникновением геометрии пространства-времени. Эта работа, подобно тщательному удалению лишнего в архитектуре, стремится к ясности в понимании голографической дуальности. Как отмечал Людвиг Витгенштейн: «Предел моего языка есть предел моего мира». Понимание ограничений используемых инструментов и моделей, как это демонстрируется применением уравнений Швингера-Дисона и симметрии реплик, необходимо для построения последовательной картины, в которой сложность уступает место элегантной компрессии без потерь.

Что дальше?

Представленная работа, хотя и демонстрирует определённую ясность в исследовании статистических свойств одноточечных функций в модели SYK, не решает, а лишь подчёркивает фундаментальную сложность установления связи между, казалось бы, абстрактными математическими конструкциями и геометрией пространства-времени. Иллюзия «магических состояний» и их потенциальная связь с червоточинами требует не столько дальнейшего подтверждения, сколько более строгой деконструкции. Необходимо отделить истинное предсказание от математической элегантности.

Ограничения, связанные с использованием приближения репликальной симметрии, остаются существенными. Неустойчивость этого приближения в ряде случаев указывает на необходимость разработки методов, способных учитывать флуктуации, выходящие за рамки упрощённых схем. Более того, зависимость от уравнений Швингера-Дисона, хоть и полезная, не является панацеей. Поиск альтернативных, возможно, более компактных, способов вычисления тепловых корреляторов представляется плодотворной задачей.

В конечном итоге, истинное значение этой работы заключается не в открытии новых феноменов, а в постановке более глубоких вопросов. Необходима критика, а не восхищение. Перспективы лежат не в усложнении моделей, а в их упрощении, в поиске минимальных принципов, способных описать наблюдаемую реальность. Иначе, все эти «червоточины» останутся лишь красивыми математическими артефактами.

Оригинал статьи: https://arxiv.org/pdf/2602.12339.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-17 00:11