Хаос на грани гравитации: связь между фермионами и CFT

Автор: Денис Аветисян

Новое исследование раскрывает глубокую связь между трехмерной гравитацией, фермионными системами и проявлениями квантического хаоса в конформных теориях поля.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал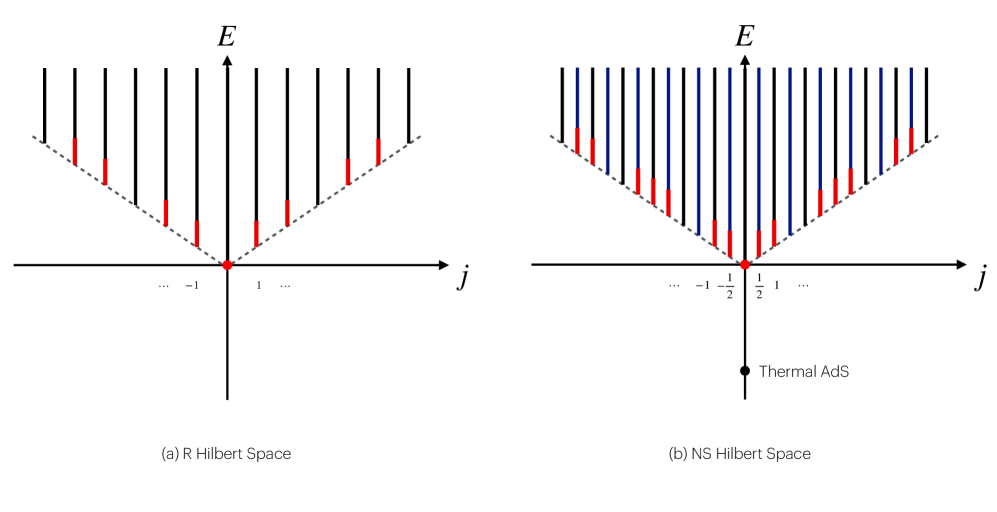

Исследование спектра чисто гравитации фермионного типа на торе выявило существование состояний, соответствующих чёрным дырам, проявляющихся при энергиях, превышающих абсолютное значение углового момента <span class="katex-eq" data-katex-display="false">E \geq |j|</span>, где <span class="katex-eq" data-katex-display="false">j</span> - целое число; при этом, для секторов Рамон и Неве, чёрные дыры бозонного типа и фермионные состояния с полуцелым угловым моментом <span class="katex-eq" data-katex-display="false">j \in \mathbb{Z} + 1/2</span> демонстрируют схожие энергетические профили, а наличие отрицательных энергий характеризуется наличием специфического края, обратно пропорционального корню из разности энергии и углового момента. — Исследование спектра чисто гравитации фермионного типа на торе выявило существование состояний, соответствующих чёрным дырам, проявляющихся при энергиях, превышающих абсолютное значение углового момента $E \geq |j|$ , где $j$ — целое число; при этом, для секторов Рамон и Неве, чёрные дыры бозонного типа и фермионные состояния с полуцелым угловым моментом $j \in \mathbb{Z} + 1/2$ демонстрируют схожие энергетические профили, а наличие отрицательных энергий характеризуется наличием специфического края, обратно пропорционального корню из разности энергии и углового момента.

Исследование демонстрирует соответствие спектральной функции формы характеристикам хаотических систем в рамках голографической дуальности и случайных матричных теорий.

Несмотря на успехи в изучении голографической дуальности, связь между гравитационными системами с фермионами и характеристиками квантового хаоса в соответствующих конформных теориях поля (КТП) остается недостаточно исследованной. В работе «3D Gravity and Chaos in CFTs with Fermions» предложена теория трехмерной гравитации с фермионами, описываемая данными двухмерной фермионной КТП, и проанализированы ее характеристики, включая спектральные свойства и статистику, полученные из анализа тороидальных отростков. Показано, что данная теория обладает микросостояниями фермионных черных дыр, даже в отсутствие материи в объеме, а полученные спектральные характеристики согладуются с предсказаниями классификации фермионных 2D КТП и случайной матричной теорией. Каким образом эти результаты могут пролить свет на природу квантовой гравитации и ее связь с хаотическими системами?

Топологические аномалии и симметрии: Игра с правилами пространства-времени

Для построения непротиворечивой теории квантовой гравитации необходимо уделять пристальное внимание аномалиям — отклонениям от ожидаемых симметрий. Эти отклонения не являются простыми помехами, а фундаментально связаны со структурой пространства-времени на квантовом уровне. В частности, аномалии могут приводить к нарушению сохраняющихся токов и, как следствие, к потере предсказуемости теории. Игнорирование аномалий может приводить к физически нереалистичным результатам, например, к появлению нефизических полюсов в амплитудах рассеяния или к нарушению принципа локальности. Поэтому, при разработке теории квантовой гравитации, необходимо тщательно анализировать все возможные аномалии и находить механизмы для их устранения или компенсации, что является одним из ключевых условий для обеспечения внутренней согласованности и предсказательной силы теории.

Аномалии в квантовой теории поля тесно связаны с топологической классификацией многообразий посредством теории кобордизмов, что предоставляет фундаментальную основу для понимания их происхождения. Кобордизмы, по сути, описывают способы «склеивания» многообразий, формируя новые, более сложные структуры, и именно эта геометрия определяет допустимые аномалии. Исследования показывают, что аномалии не являются случайными отклонениями, а отражают глубокие топологические свойства пространства-времени, определяемые структурой кобордизмов. Этот подход позволяет классифицировать аномалии на основе топологических инвариантов, таких как числа Бетти и характеристика Эйлера, что, в свою очередь, накладывает ограничения на допустимые теории квантовой гравитации. Понимание этой связи открывает путь к построению самосогласованных моделей, в которых аномалии не приводят к противоречиям, а являются неотъемлемой частью геометрии пространства-времени.

Присутствие фермионов, частиц с полуцелым спином, оказывает существенное влияние на допустимые конфигурации симметрий в квантовой теории поля и гравитации. Это связано с тем, что фермионы описываются спинорами, математическими объектами, требующими для своего корректного определения специфических граничных условий, задаваемых спинорной структурой многообразия. Спинорная структура определяет, как спиноры преобразуются при непрерывных деформациях пространства-времени, и именно она накладывает ограничения на допустимые симметрии. В частности, несовместимость спинорной структуры с определенной симметрией может приводить к возникновению аномалий — нарушений симметрии на квантовом уровне. Таким образом, изучение спинорных структур не только необходимо для корректного описания фермионных полей, но и играет ключевую роль в понимании фундаментальных свойств пространства-времени и допустимых симметрий в физике.

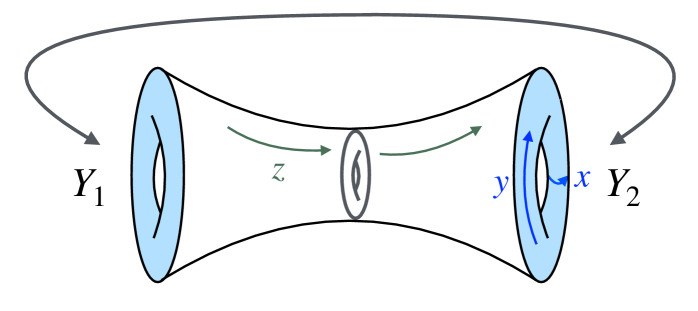
Инвариант кобордизма на многообразии с границей вычисляется локально на компактном многообразии путем добавления многообразия, соединяющего две 2-тороидальные границы с отличающимися спиновыми структурами, вызванными вставкой дефекта коразмерности один вдоль серого тора, после чего происходит склеивание внешних границ для получения 3-мерного отображающего тора.

Голографическая дуальность: Перевод гравитации на язык конформных теорий

Исследование трехмерной гравитации с фермионами представляет собой основу для изучения голографической дуальности — связи с двумерной конформной теорией поля (КТП). Данный подход позволяет рассматривать гравитационные системы в трехмерном пространстве-времени как эквивалентные КТП, описывающей физические явления на двумерной границе. Изучение свойств трехмерной гравитации с фермионами обеспечивает инструмент для проверки и углубления понимания голографического принципа, который предполагает, что гравитация может возникать как эмерджентное свойство квантовой теории на границе пространства-времени. Это направление исследований позволяет решать сложные гравитационные задачи путем перевода их в более доступные для анализа рамки КТП, и наоборот.

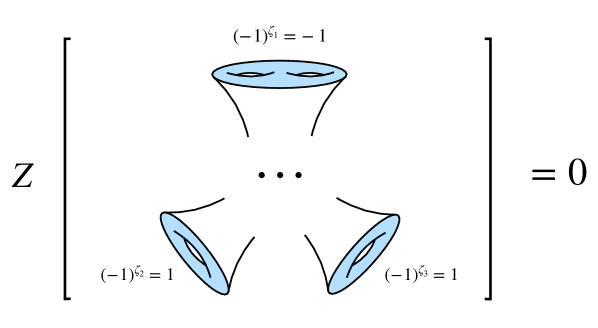
Модулярная инвариантность, представляющая собой симметрийное условие для функции разделения $Z$ , является критически важным требованием для обеспечения непротиворечивости гравитационных вычислений в данной модели. Нарушение модулярной инвариантности приводит к появлению физически нереалистичных результатов и неустойчивостей. Выбор спиновой структуры оказывает непосредственное влияние на модулярную инвариантность функции разделения, поскольку различные спиновые структуры приводят к различным преобразованиям при модулярных преобразованиях. Следовательно, для получения корректных гравитационных решений необходимо тщательно учитывать влияние спиновой структуры на обеспечение модулярной инвариантности функции разделения.

Данная дуальность позволяет преобразовать задачи гравитации в термины конформной теории поля (КТП), открывая новые возможности для анализа. В частности, сложные вычисления в гравитационном контексте могут быть заменены на эквивалентные, но часто более простые, вычисления в КТП. Это особенно полезно при исследовании сильносвязанных систем, где стандартные методы теории возмущений оказываются неэффективными. Перевод задачи в пространство КТП позволяет использовать инструменты и техники, разработанные для этой теории, для получения информации о гравитационной системе, и наоборот. Такой подход предоставляет альтернативные методы решения задач и проверки результатов в обеих областях физики.

Интеграл по гравитационному пути с 2D спиновыми поверхностями на границе обращается в нуль, если сумма индексов <span class="katex-eq" data-katex-display="false">\sum_{i}\zeta_{i}</span> кратна единице по модулю два, при этом ненулевые значения ζ исключают существование соответствующей 3D спиновой поверхности, что верно как для объединения торов, так и для более общих поверхностей. — Интеграл по гравитационному пути с 2D спиновыми поверхностями на границе обращается в нуль, если сумма индексов $\sum_{i}\zeta_{i}$ кратна единице по модулю два, при этом ненулевые значения ζ исключают существование соответствующей 3D спиновой поверхности, что верно как для объединения торов, так и для более общих поверхностей.

Спектральный хаос и теория случайных матриц: Увидеть порядок в случайности

Спектральная форма фактора (СФФ) является ключевым индикатором квантового хаоса в двойной конформной теории поля (КТП). СФФ, определяемый как $\langle Z(t)Z(0) \rangle$ , где $Z(t)$ — оператор перенормировки, отражает корреляции в спектре оператора Гамильтона. Отклонение СФФ от поведения, предсказываемого для интегрируемых систем, указывает на наличие хаотического поведения. В частности, для хаотических систем СФФ демонстрирует линейный рост во времени, что является характерным признаком, позволяющим количественно оценить степень хаотичности в исследуемой КТП. Анализ СФФ позволяет выявить и охарактеризовать хаотические флуктуации в спектральных свойствах системы, предоставляя важные сведения о ее динамике.

Теория случайных матриц (ТCM) предоставляет эффективный инструментарий для моделирования статистических свойств хаотических систем. В рамках ТCM, ансамбли случайных матриц используются для описания энергетических уровней и других наблюдаемых величин в хаотических системах, позволяя получить предсказания о их статистическом распределении. Функтор спектральной формы (SFF), являясь ключевым индикатором квантового хаоса, сравнивается с предсказаниями ТCM для проверки соответствия и количественной оценки степени хаотичности системы. Согласие между SFF и результатами ТCM служит важным подтверждением хаотического поведения, поскольку ТCM представляет собой универсальную модель для систем, демонстрирующих отсутствие регулярности и предсказуемости.

В рамках исследования хаотичности в двойной конформной теории поля (CFT) используется фреймворк RMT2, позволяющий установить связь между спектральной формой фактора (SFF) и модульным дополнением данных, полученных из случайных матриц. Фреймворк RMT2 позволяет количественно оценить хаотическое поведение системы, анализируя соответствие SFF предсказаниям, основанным на статистических свойствах случайных матриц $\mathcal{S}(t) \approx \text{const.} + \frac{\log t}{2\pi}$ , что является ключевым аргументом в подтверждение хаотичности дуальной CFT.

Эффекты объемной TQFT в высших измерениях могут быть изучены с помощью скрученных склеек, проявляющихся в отталкивании границ чёрной дыры в виде клина после применения преобразования <span class="katex-eq" data-katex-display="false"> \xi \xi </span> (которое может быть большим диффеоморфизмом, чётностью фермионов, <span class="katex-eq" data-katex-display="false"> \mathbb{R}T </span> и т.д.) и в индуцированной модификации спектра чёрной дыры при склейке двух чёрных дыр по их границам с одним и тем же <span class="katex-eq" data-katex-display="false"> \xi \xi </span>-скручиванием. — Эффекты объемной TQFT в высших измерениях могут быть изучены с помощью скрученных склеек, проявляющихся в отталкивании границ чёрной дыры в виде клина после применения преобразования $\xi \xi$ (которое может быть большим диффеоморфизмом, чётностью фермионов, $\mathbb{R}T$ и т.д.) и в индуцированной модификации спектра чёрной дыры при склейке двух чёрных дыр по их границам с одним и тем же $\xi \xi$ -скручиванием.

Чётность фермионов и гравитационные ограничения: Симметрии как стражи непротиворечивости

Единая ℤ2-симметрия, представляющая четность фермионов в конформной теории поля (КТП), накладывает существенные ограничения на вычисления в гравитации. Эта симметрия, по сути, диктует, что фермионы должны сохранять свою четность — то есть, их свойства должны оставаться неизменными при отражении. В контексте гравитационных расчетов, нарушение этой симметрии приводит к появлению аномалий, которые могут дестабилизировать теорию и сделать ее несогласующейся. Поэтому, ℤ2-симметрия выступает в роли фундаментального принципа, гарантирующего внутреннюю согласованность трехмерной гравитации, включающей фермионы, и требует особого внимания при анализе гравитационных взаимодействий с участием этих частиц. Наложение ограничений, обусловленных данной симметрией, является ключевым шагом в построении корректной и физически обоснованной теории гравитации.

Нарушения симметрии ℤ2, представляющей четность фермионов, проявляются в виде аномалий, оказывающих существенное влияние на согласованность трехмерной гравитации с фермионами. Эти аномалии возникают как следствие квантовых эффектов и приводят к расхождениям в вычислениях, требуя введения регуляризаций или контртермов для обеспечения физической осмысленности теории. Существование аномалий указывает на то, что симметрия, кажущаяся классически, не сохраняется на квантовом уровне, что может приводить к нестабильности или нефизическим предсказаниям. Таким образом, поддержание согласованности теории требует тщательного баланса между сохранением симметрии, устранением аномалий и обеспечением физической адекватности гравитационного взаимодействия с фермионными полями. Понимание этих взаимосвязей критически важно для построения непротиворечивых моделей гравитации в рамках конформной теории поля.

Исследования показывают, что согласованность гравитационных теорий, включающих фермионы, напрямую зависит от тонкого равновесия между фундаментальными симметриями и возникающими аномалиями. Нарушение симметрий, таких как четность фермионов, проявляется в виде аномалий, которые могут привести к математической несогласованности теории. $ℤ₂$ симметрия, представляющая четность фермионов в конформной теории поля, накладывает строгие ограничения на расчеты в гравитации, и любые отклонения от нее требуют тщательного анализа. Установлено, что поддержание этого баланса — необходимое условие для построения физически осмысленных и математически корректных моделей гравитации, взаимодействующих с фермионной материей, подчеркивая важность симметрий как краеугольного камня современной теоретической физики.

В гравитационном функциональном интеграле интегрирование происходит по всем многообразиям <span class="katex-eq" data-katex-display="false">X_D</span> с объемной спиновой структурой, совместимой со спиновой структурой и метрикой границы <span class="katex-eq" data-katex-display="false">Y_{D-1}</span>. — В гравитационном функциональном интеграле интегрирование происходит по всем многообразиям $X_D$ с объемной спиновой структурой, совместимой со спиновой структурой и метрикой границы $Y_{D-1}$ .

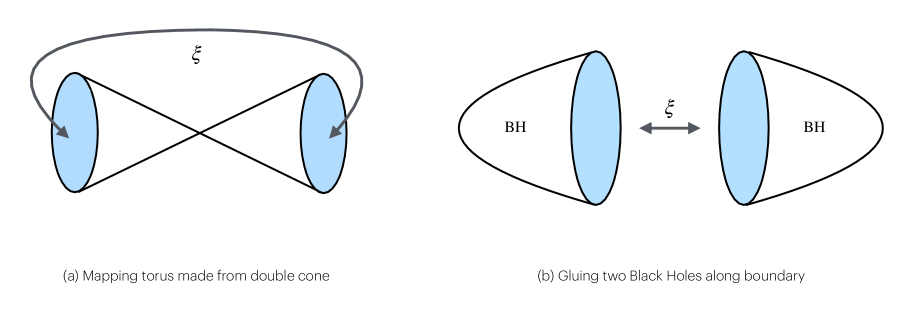
Голографическая дуальность: Новый взгляд на хаос: Заглянуть за горизонт событий

Голографическая дуальность предоставляет уникальный инструмент для изучения квантового хаоса в гравитационных системах. Суть подхода заключается в установлении соответствия между гравитационной системой в некотором объеме и квантово-полевой теорией (КФТ) на границе этого объема — подобно голограмме, где трехмерное изображение кодируется на двумерной поверхности. Это позволяет трансформировать чрезвычайно сложные гравитационные задачи, которые трудно поддаются анализу, в более доступные для исследования задачи КФТ. Изучая хаотическое поведение в КФТ, ученые могут получить ценные сведения о квантовом хаосе в соответствующих гравитационных системах, таких как черные дыры, и углубить понимание фундаментальных свойств пространства-времени. Такой подход открывает принципиально новые возможности для исследования сложных физических явлений, недоступных традиционным методам.

Данное соответствие, известное как голографическая дуальность, позволяет преобразовать задачи гравитации в термины конформной теории поля (КТП), открывая новые возможности для анализа. В частности, сложные вычисления в гравитационном контексте могут быть заменены на эквивалентные, но часто более простые, вычисления в КТП. Это особенно полезно при исследовании сильносвязанных систем, где стандартные методы теории возмущений оказываются неэффективными. Перевод задачи в пространство КТП позволяет использовать инструменты и техники, разработанные для этой теории, для получения информации о гравитационной системе, и наоборот. Такой подход предоставляет альтернативные методы решения задач и проверки результатов в обеих областях физики.

Дальнейшее изучение голографической дуальности открывает перспективы для углубленного понимания природы гравитации, квантового хаоса и фундаментальных законов Вселенной. Предполагается, что эта дуальность — не просто математическая аналогия, а отражение глубокой связи между различными физическими системами, позволяющее решать сложные задачи в гравитации посредством более простых расчетов в рамках конформной теории поля $CFT$ . Исследователи полагают, что анализ квантовых флуктуаций в $CFT$ может пролить свет на поведение черных дыр и раннюю Вселенную, раскрывая тайны, скрытые в экстремальных гравитационных условиях. В частности, изучение хаотических процессов в гравитационных системах через призму голографической дуальности способно привести к созданию новых моделей, описывающих поведение материи при сверхвысоких энергиях и плотностях, приближая науку к пониманию самых фундаментальных аспектов реальности.

В данном разделе вычисляется двумерный тороидальный червоточина с граничными модулями <span class="katex-eq" data-katex-display="false">$\\tau\\_{1},\\bar{\\tau}\\_{1}$</span> и <span class="katex-eq" data-katex-display="false">$\\tau\\_{2},\\bar{\\tau}\\_{2}$</span>, а также спиновой структурой <span class="katex-eq" data-katex-display="false">$\\mathfrak{s}\\_{1}$</span> и <span class="katex-eq" data-katex-display="false">$\\mathfrak{s}\\_{2}$</span>. — В данном разделе вычисляется двумерный тороидальный червоточина с граничными модулями $\\tau\\_{1},\\bar{\\tau}\\_{1}$ и $\\tau\\_{2},\\bar{\\tau}\\_{2}$ , а также спиновой структурой $\\mathfrak{s}\\_{1}$ и $\\mathfrak{s}\\_{2}$ .

Исследование демонстрирует, что понимание взаимосвязи между гравитацией, квантовым хаосом и теорией случайных матриц требует глубокого анализа базовых принципов. Как отмечал Юрген Хабермас: «Коммуникативное действие направлено на достижение взаимопонимания». Данная работа, исследуя спектральную форму фактора и его соответствие хаотическому поведению в дуальной 2D конформной теории поля, фактически предлагает новый способ «коммуникации» между различными областями физики. Анализ фермионной 3D гравитации, представленный в исследовании, показывает, что система, кажущаяся сложной, может быть понята через выявление внутренних закономерностей и связей, что соответствует философии глубокого проникновения в суть явления.

Что дальше?

Представленная работа, по сути, лишь приоткрыла ящик Пандоры. Утверждение о связи фермионной 3D гравитации, квантического хаоса и случайных матриц — это не столько доказательство, сколько приглашение к дальнейшему препарированию. Истинная проверка этой связи лежит не в уточнении существующих расчётов, а в поиске совершенно новых, неожиданных проявлений хаотического поведения в дуальных 2D конформных теориях поля. Необходимо отбросить предубеждения о «естественности» спектральных функций и смело искать отклонения от предсказанных шаблонов.

Особый интерес представляет вопрос о границах применимости полученных результатов. До каких пор эта аналогия с хаотическими системами остаётся валидной? Существуют ли качественно новые эффекты, возникающие при изменении параметров теории или при переходе к более сложным системам? Игнорирование этих вопросов — преступление против разума. Очевидно, что исследование спектральных корреляторов — лишь верхушка айсберга, а под поверхностью скрываются гораздо более глубокие и фундаментальные закономерности.

В конечном счёте, эта работа — не конец пути, а лишь отправная точка. Она демонстрирует, что даже в самых, казалось бы, устоявшихся областях физики всегда есть место для неожиданных открытий и радикальных переосмыслений. Задача состоит не в том, чтобы подтвердить существующие теории, а в том, чтобы разрушить их и построить новые, более точные и полные модели реальности.

Оригинал статьи: https://arxiv.org/pdf/2602.17618.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-21 23:51