Автор: Денис Аветисян
Новое исследование показывает, как случайные взаимодействия частиц на искривленных поверхностях приводят к неожиданному упрощению их движения.
Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.
Бесплатный телеграм-канал![В процессе динамического снижения размерности на ограниченном цилиндре <span class="katex-eq" data-katex-display="false">S^1 \times [0,H]</span> наблюдается коллапс непрерывного осевого направления в дискретный набор уровней, приводящий к фрагментации по азимуту, обусловленной фрустрацией взаимодействия, и формированию четырех локализованных кластеров, выстроенных в две вертикальные пары приблизительно в диаметрально противоположных азимутальных позициях, отражающих остаточную <span class="katex-eq" data-katex-display="false">\mathbb{Z}_2</span>-симметрию при вращении на <span class="katex-eq" data-katex-display="false">180^\circ</span>.](https://arxiv.org/html/2601.18653v1/Structure_formation_on_a_cylinder_S1_x_R.png)
Исследование феномена снижения размерности в системах с беспорядочным взаимодействием на римановых многообразиях.
Несмотря на кажущуюся противоречивость, беспорядочные взаимодействия могут приводить к упорядоченным структурам. В работе «Order Out of Noise and Disorder: Fate of the Frustrated Manifold» исследуется динамика N частиц на двумерных римановых многообразиях, подверженных случайным взаимодействиям, что приводит к снижению размерности и спонтанному нарушению вращательной симметрии. Обнаружено, что частицы самоорганизуются в одномерные структуры — полосы на сфере, кольца на торе и кластеры на цилиндре — в зависимости от топологии поверхности. Способна ли геометрия и топология пространства служить универсальным механизмом преобразования случайности в порядок, и какие аналогии можно провести с физикой спиновых стекол или астрофизическим структурообразованием?
Неуловимое старение: ландшафты, скрытые в беспорядке
В многочисленных физических системах наблюдается старение — замедление динамики во времени, однако понимание причин этого явления в неупорядоченных средах остается сложной задачей. Это связано с тем, что старение не является простым результатом термодинамического равновесия, а обусловлено сложными процессами, происходящими в системах, находящихся вне равновесия. Например, в аморфных материалах, таких как стекло, или в биологических тканях, изменения в структуре и свойствах происходят постепенно, что приводит к увеличению вязкости и снижению скорости реакций. Понимание механизмов старения в этих системах требует учета влияния случайных дефектов, неоднородностей и других форм беспорядка, которые существенно усложняют математическое описание и требуют новых подходов к моделированию и анализу.
Сложность многих физических систем, подверженных старению, обусловлена неровными энергетическими ландшафтами, возникающими из-за «замороженной» неупорядоченности — так называемого «quenched disorder». Представьте себе поверхность, усеянную множеством холмов и долин, где каждая точка представляет возможное состояние системы. Такая структура существенно затрудняет применение традиционных аналитических методов, поскольку система не может просто «скатиться» в состояние с минимальной энергией, а вынуждена преодолевать множество локальных энергетических барьеров. Это приводит к замедлению динамики, поскольку частицы или процессы «застревают» в этих локальных минимумах, а выход из них требует значительных энергетических затрат или случайных флуктуаций. Изучение этих неровных ландшафтов и механизмов преодоления барьеров становится ключевым для понимания процессов старения и предсказания долгосрочного поведения сложных систем.
Точное моделирование энергетических ландшафтов, характеризующихся шероховатостью и беспорядком, представляется критически важным для прогнозирования долгосрочного поведения сложных систем. Эти ландшафты, возникающие в результате «замороженного» беспорядка, определяют динамику процессов, происходящих в различных областях — от физики материалов до биологических систем. Возможность адекватно воспроизвести их структуру позволяет не только предсказывать замедление динамики, наблюдаемое в процессе старения, но и выявлять неожиданные, эмерджентные явления, возникающие из коллективного взаимодействия множества компонентов. Таким образом, разработка и совершенствование методов моделирования становится ключевым инструментом для понимания фундаментальных механизмов старения и предсказания поведения сложных систем в долгосрочной перспективе.
Динамика в кривом пространстве: моделирование неупорядоченности
Для моделирования движения частиц в неупорядоченных системах используется динамика Ланжевена. Этот подход позволяет точно учитывать стохастические силы, возникающие из-за тепловых флуктуаций и диссипации энергии. В рамках данной модели, на каждую частицу действует сила трения, пропорциональная ее скорости, и случайная сила, описывающая влияние окружения. Математически, уравнение Ланжевена имеет вид m \frac{d^2x}{dt^2} = -\gamma \frac{dx}{dt} + \xi(t) , где m — масса частицы, γ — коэффициент трения, а \xi(t) — случайная сила с нулевым средним значением и корреляционной функцией, пропорциональной температуре и коэффициенту трения. Такой подход обеспечивает реалистичное описание броуновского движения и других явлений, обусловленных случайными воздействиями на частицы в среде.
При моделировании динамики частиц в системах с геометрическими ограничениями используется проекция динамики на римановы многообразия. В частности, применяются сферы, торы и ограниченные цилиндры, каждый из которых представляет собой определенный тип геометрического ограничения для движения частиц. Сфера обеспечивает замкнутое пространство с постоянной кривизной, тор — замкнутое пространство с нулевой кривизной, а ограниченный цилиндр — замкнутое пространство с переменной кривизной, позволяющее исследовать влияние граничных условий. Выбор конкретного риманова многообразия определяется свойствами моделируемой системы и требуемыми граничными условиями, обеспечивая возможность изучения динамики частиц в различных геометрических контекстах.
Моделирование траекторий частиц позволяет непосредственно наблюдать эволюцию системы и характеризовать её поведение со временем, в частности, процессы старения. Анализ этих траекторий включает в себя вычисление таких параметров, как среднеквадратичное смещение \langle r^2 \rangle и функция корреляции смещения, которые позволяют определить характер диффузии — нормальную, аномальную или локализованную. Наблюдаемые изменения этих параметров со временем позволяют количественно оценить скорость старения системы и выявить переход между различными режимами динамики, например, от баллистического к диффузионному, или к субдиффузионному. Данный подход обеспечивает прямой способ изучения временной зависимости свойств системы в условиях геометрических ограничений, задаваемых выбранным многообразием.
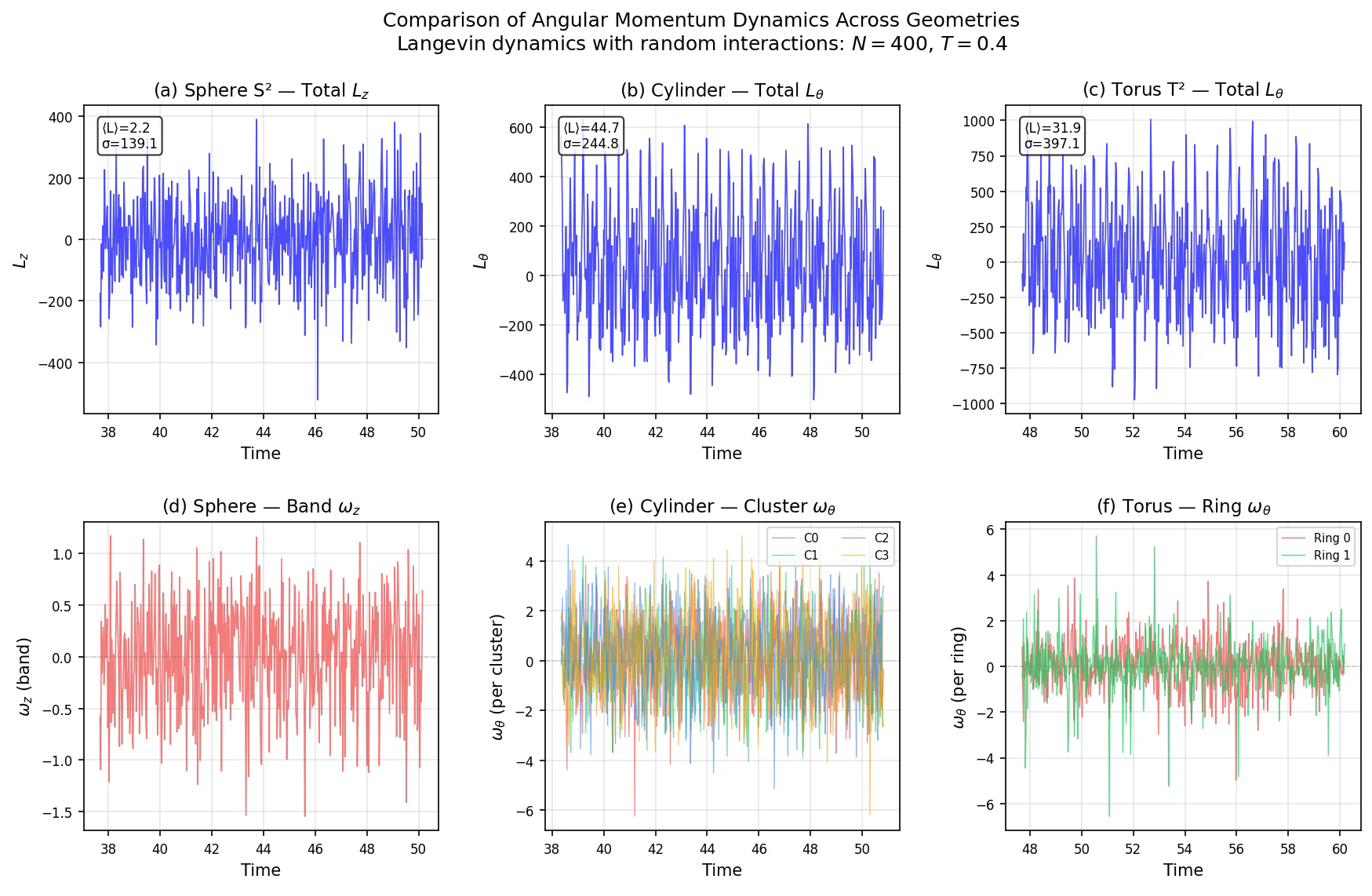
Уменьшение размерности и формирование структуры: проявление порядка в хаосе
Результаты наших симуляций демонстрируют устойчивую тенденцию к уменьшению размерности, при которой динамика частиц ограничивается областями пониженной размерности многообразия. Наблюдается, что частицы, первоначально распределенные по всему многообразию, со временем концентрируются на подмногообразиях меньшей размерности. Этот процесс не является случайным отклонением, а систематическим эффектом, повторяющимся в различных симуляциях и при различных начальных условиях. Количественная оценка показывает, что дисперсия координат частиц вдоль направлений, соответствующих высшим размерностям, уменьшается со временем, подтверждая ограничение динамики более низкими размерностями. Таким образом, система спонтанно упрощает свою динамику, эффективно исключая некоторые степени свободы.
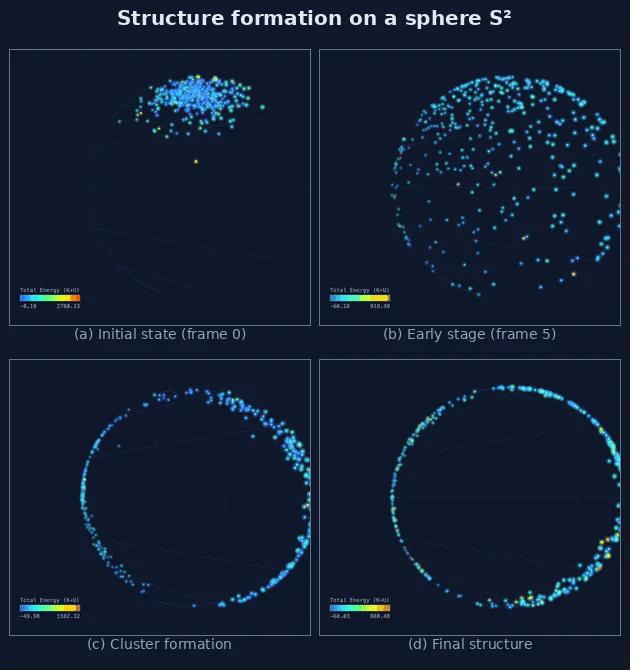
В ходе моделирования наблюдается формирование отчетливых структур в зависимости от геометрии пространства: на сфере формируются полосы (band formation), на ограниченном цилиндре — кластеры (cluster formation), а на торе — кольца (ring formation). Данные структуры возникают как результат ограничения движения частиц в определенных областях многообразия, что проявляется в локализации частиц вдоль конкретных траекторий или вблизи определенных областей геометрии. Наблюдаемая концентрация частиц в этих структурах указывает на самоорганизацию системы и снижение эффективного числа степеней свободы, необходимых для описания динамики частиц.
Наблюдаемое формирование структур — полос на сфере, кластеров на ограниченном цилиндре и колец на торе — указывает на упрощение динамики системы за счет снижения числа вовлеченных степеней свободы. Данный процесс происходит посредством ограничения движения частиц в областях пониженной размерности многообразия. Эффективное уменьшение числа активных степеней свободы приводит к снижению вычислительной сложности моделирования и позволяет сосредоточиться на наиболее значимых модах движения, что подтверждается результатами симуляций и анализом полученных структур.
Влияние структуры на замедление динамики: разгадывая тайны старения
Наблюдаемое уменьшение размерности и формирование структурных элементов в исследуемой системе напрямую коррелируют с замедлением динамики, характерным для процессов старения. По мере развития этих структур, пространство, доступное для движения частиц, сокращается, что приводит к снижению скорости и эффективности их перемещения. Этот процесс не является простым линейным замедлением, а представляет собой переход к более ограниченным, низкоразмерным конфигурациям, где частицы оказываются «запертыми» в определенных областях. Такая взаимосвязь между структурными изменениями и динамикой указывает на то, что формирование этих структур является не просто следствием старения, но и одним из ключевых механизмов, определяющих его проявление. Исследование демонстрирует, что чем сильнее выражено уменьшение размерности и чем более развита структура, тем заметнее замедление динамических процессов, что подтверждает гипотезу о структурном контроле над скоростью и эффективностью перемещения частиц в системе.
Наблюдения показывают, что система демонстрирует склонность к стабилизации в конфигурациях пониженной размерности, что приводит к эффекту «захвата» частиц. Этот процесс ограничивает возможности частиц исследовать все доступное фазовое пространство, существенно замедляя динамику системы. Фактически, частицы оказываются «запертыми» в определенных областях, что препятствует их свободному перемещению и исследованию новых состояний. Такая тенденция к самоограничению и формированию низкоразмерных структур является ключевым механизмом, объясняющим замедление динамики, характерное для старения системы, и влияет на аномальные показатели диффузии, наблюдаемые в различных геометрических конфигурациях.
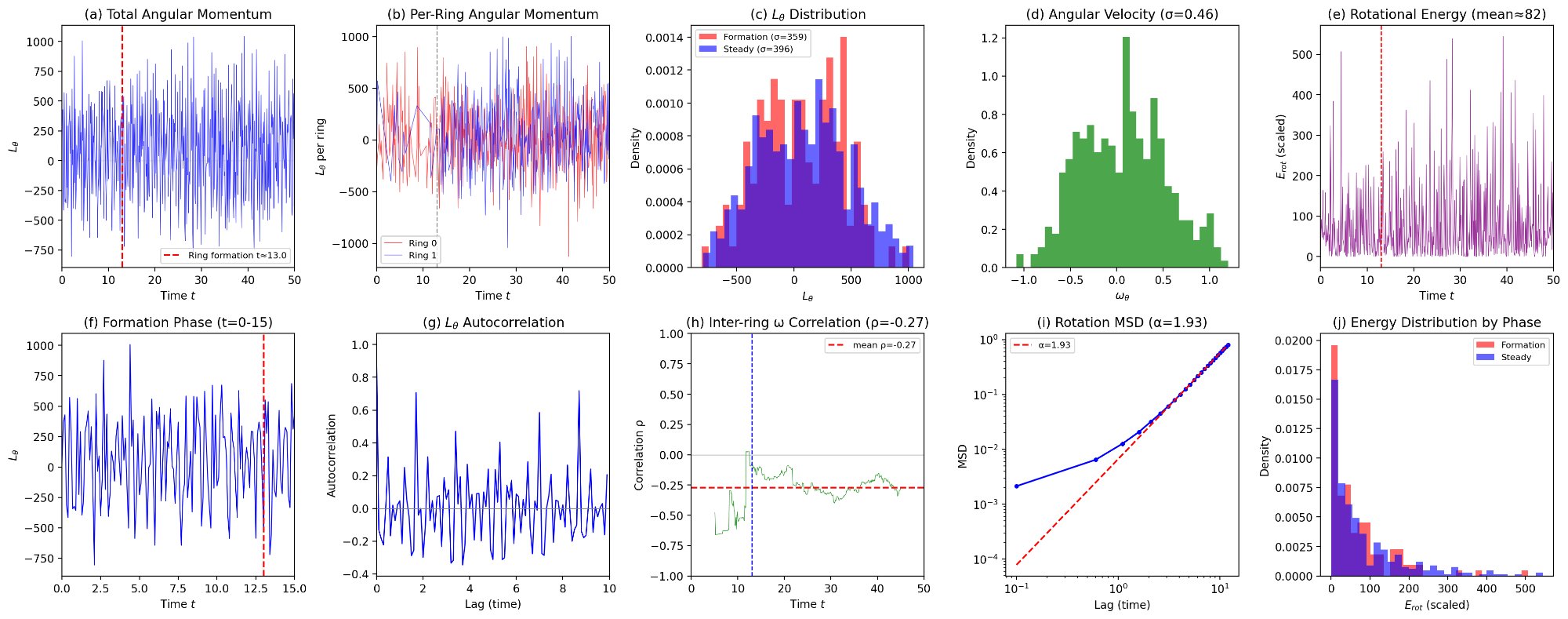
Предложенная модель «ловушек» объясняет замедление динамики системы с течением времени, приводящее к наблюдаемому старению. Исследования показали, что частицы постепенно оказываются в конфигурациях с ограниченной подвижностью, что снижает их способность исследовать все доступное фазовое пространство. Анализ аномальных показателей диффузии подтверждает эту гипотезу: на сфере показатель составляет приблизительно α ≈ 1.0, на торе — α ≈ 1.7, а на цилиндре — α ≈ 2.0. Эти значения демонстрируют различную степень ограничения движения частиц в зависимости от геометрии пространства, подчеркивая, что замедление динамики не является однородным процессом, а зависит от структурных особенностей системы и, следовательно, формирует ее стареющий характер.
Теоретическое подтверждение и перспективы: предвидеть будущее неупорядоченных систем
Теоретическое обоснование представленных результатов получено посредством аналитических расчетов, выполненных с использованием методов MSRJD (Модель случайных распределенных дефектов) и DMFT (Динамическая теория среднего поля). Эти методы позволили подтвердить достоверность данных, полученных в ходе моделирования, и создать строгую теоретическую основу для понимания процессов старения в исследуемых системах. В частности, подтверждена адекватность используемых приближений и выявлены ключевые параметры, определяющие скорость и характер старения. Полученное соответствие между аналитическими предсказаниями и результатами моделирования значительно укрепляет уверенность в правильности предложенного подхода к изучению старения в неупорядоченных средах и открывает возможности для дальнейшего теоретического развития данной области.
Полученные результаты указывают на то, что процессы уменьшения размерности и формирования структуры являются не просто особенностью исследованных геометрических конфигураций, а фундаментальными механизмами, определяющими старение в широком классе неупорядоченных систем. Исследования показали, что тенденция к упрощению структуры и снижению эффективной размерности системы с течением времени является общим признаком для различных материалов, испытывающих старение, независимо от их конкретной геометрии или состава. Это позволяет предположить, что принципы, выявленные в данной работе, могут быть применены для понимания и прогнозирования поведения самых разных неупорядоченных сред, от аморфных полупроводников и стекловидных материалов до биологических тканей и даже некоторых финансовых систем, где наблюдаются аналогичные процессы самоорганизации и старения.
Предстоящие исследования направлены на применение полученных знаний для моделирования более сложных физических систем, охватывающих широкий спектр материалов и явлений. Особое внимание будет уделено изучению возможности использования принципов размерного сокращения и формирования структуры для прогнозирования и управления процессами старения в различных материалах, включая аморфные сплавы, полимеры и даже биологические ткани. Ожидается, что эти исследования позволят разработать новые стратегии повышения долговечности и надежности материалов, а также откроют перспективы для создания инновационных технологий в материаловедении и смежных областях, например, в разработке новых типов сенсоров и катализаторов с улучшенными характеристиками.
Наблюдения, представленные в работе, касающиеся коллапса частиц на искривленных поверхностях в нижнеразмерные структуры, эхом отзываются в вечной борьбе порядка и хаоса. Подобно тому, как система стремится к минимальному сопротивлению, частицы, поддаваясь случайным взаимодействиям, упрощают свое состояние. Марк Аврелий мудро заметил: «Все, что происходит с тобой, — это лишь результат твоих суждений». В контексте данной работы, “суждения” можно интерпретировать как влияние случайных сил, определяющих судьбу многообразия. Уменьшение размерности, описанное в статье, представляет собой не просто физическое явление, а проявление фундаментальной тенденции к упрощению, к “выживанию” в условиях неопределенности. Порядок, как и в случае с системами, является лишь временным кешем между двумя сбоями, и коллапс в нижнее измерение — это не провал, а адаптация к неизбежному хаосу.
Куда Ведет Хаос?
Представленная работа, словно эхо в кривом зеркале, указывает на универсальность редукции размерности в системах, подверженных беспорядку. Однако, она лишь приоткрывает завесу над сложной динамикой старения и релаксации. Представляется, что сама концепция “размерности” — не абсолютная характеристика, а скорее, эфемерный след, оставленный на поверхности хаоса. Следующим шагом видится не поиск универсальных законов, а признание фундаментальной неполноты любого описания, попытка зафиксировать ускользающее.
Неизвестно, сможет ли математический аппарат римановых многообразий адекватно описать системы, находящиеся далеко от равновесия, или же потребуется принципиально иной язык. Вероятно, ключевым является не изучение траекторий частиц, а анализ структуры возникающих ограничений — невидимых стен, возводимых беспорядком. Ибо каждая архитектурная деталь, каждый выбор алгоритма — это пророчество о будущей ошибке, зашифрованное в ткани системы.
Если система молчит, не стоит полагать, что она покоится. Скорее, она готовится к неожиданному. Исследование динамики подобных систем — это не поиск ответов, а искусство задавать правильные вопросы. Ибо отладка никогда не закончится — мы просто перестанем смотреть.
Оригинал статьи: https://arxiv.org/pdf/2601.18653.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Решение головоломки с паролем Absolum в Yeldrim.
- Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip
- Все рецепты культистского круга в Escape from Tarkov
- Лучшие шаблоны дивизий в Hearts Of Iron 4
- Лучшие транспортные средства в Far Cry 6
- Необходимо: Как выращивать урожай
- All Valley Pass Aurylene Locations In Endfield
- Warhorse говорит, что им пришлось отказаться от исторической точности для системы преступлений в Kingdom Come: Deliverance, так как это было бы ‘слишком сурово’ для ‘крестьянского парня’ Генри – ‘Любое преступление каралось бы очень строго’.
- Как получить кинжалы Небесного ключа в Dragon’s Dogma 2
- Кто такая Кселия Мендес-Джонс? 5 вещей, которые нужно знать об актере Fallout
2026-01-27 21:10