Автор: Денис Аветисян
Новое численное моделирование показывает, как немарковские эффекты влияют на эволюцию возмущений в ранней Вселенной.
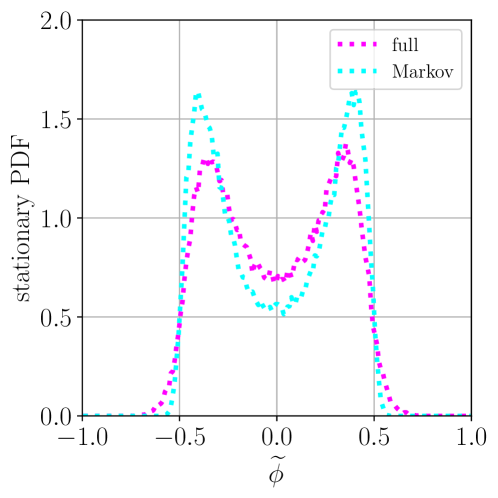
Представлено полное численное решение стохастического формализма для космологических возмущений, учитывающее немарковскую динамику и эффективные массы полей в пространстве Де Ситтера.
Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.
Бесплатный телеграм-каналВ космологических моделях, описывающих инфляционную эпоху, традиционные марковские приближения часто оказываются недостаточными для точного моделирования стохастических процессов. В данной работе, посвященной ‘Numerical simulation of the stochastic formalism including non-Markovianity’, численно исследуется стохастическая динамика космологических возмущений, учитывающая немарковский характер взаимодействия ультрафиолетовых и инфракрасных мод. Показано, что корректный учет эффективных масс и немарковских эффектов принципиально важен для эволюции полей, в частности, для анализа плоских направлений в минимальной суперсимметричной модели. Какие новые горизонты открывает учет немарковских эффектов для понимания ранней Вселенной и построения более реалистичных космологических моделей?
Отголоски Квантового Хаоса: Зарождение Вселенной из Флуктуаций
Космологическая инфляция, общепринятая модель ранней Вселенной, предоставляет теоретическую основу для понимания формирования крупномасштабной структуры, наблюдаемой сегодня. Согласно этой модели, крошечные квантовые флуктуации, возникшие в первые моменты существования Вселенной, были растянуты экспоненциальным расширением пространства-времени, действуя как зародыши для будущих галактик и скоплений галактик. Эти флуктуации, изначально квантово-механические по своей природе, стали источником неоднородностей в плотности энергии, которые под действием гравитации со временем усилились, сформировав наблюдаемую космическую сеть. Таким образом, понимание природы и эволюции этих квантовых флуктуаций является ключевым для подтверждения модели инфляции и раскрытия тайн происхождения Вселенной. Изучение спектра мощности этих флуктуаций, предсказанного различными моделями инфляции, позволяет сопоставить теоретические предсказания с наблюдательными данными реликтового излучения, предоставляя ценную информацию о физических процессах, происходивших в экстремальных условиях ранней Вселенной.
Космологические флуктуации, рассматриваемые как первоначальные возмущения, из которых впоследствии сформировались галактики и крупномасштабная структура Вселенной, требуют особого теоретического подхода. Переход от квантового мира, где господствует неопределенность, к классической картине, описывающей наблюдаемую Вселенную, представляет собой сложную задачу. Для этого необходимо разработать методы, способные корректно описать эволюцию этих флуктуаций, учитывая как квантовые эффекты на ранних стадиях, так и их последующую «классическую» эволюцию под действием гравитации. Такой подход предполагает, что изначально квантовые возмущения, представленные как \delta \phi(x) , со временем эволюционируют в классические плотности, определяющие распределение материи во Вселенной. Понимание этого перехода является ключевым для построения реалистичной модели формирования структуры Вселенной и проверки космологических теорий.
Стохастический формализм представляет собой мощный инструмент для анализа квантовых флуктуаций, возникших в ранней Вселенной и послуживших зародышами крупномасштабной структуры. Вместо прямого решения сложных уравнений квантовой теории поля, этот подход моделирует флуктуации как стохастические процессы, подобно броуновскому движению. Суть метода заключается в эффективном «исключении» высокоэнергетических мод, не наблюдаемых в современных масштабах, посредством методов эффективной теории поля. Это позволяет перейти от сложного квантового описания к более простому, классическому, описывающему эволюцию флуктуаций плотности Вселенной. Такой подход не только упрощает вычисления, но и позволяет получить предсказания о статистических свойствах космического микроволнового фона и распределении галактик, которые могут быть проверены наблюдениями. \delta \rho(x) = \in t d^3k A(k) e^{i k \cdot x} — пример представления флуктуаций плотности в рамках стохастического формализма.
Разделение Масштабов: От Длинных Волн к Квантовому Шуму
Стохастическая формализация базируется на раздельном подходе к рассмотрению длинноволновых (ИК) и коротковолновых (УФ) мод. Длинноволновые моды, характеризующиеся низкими энергиями и большими длинами волн, рассматриваются как классические, то есть их динамика описывается детерминированными уравнениями. В то же время, коротковолновые моды, соответствующие высоким энергиям и малым длинам волн, трактуются как квантово-механические, что предполагает учет их квантовых флуктуаций и дискретности энергетических уровней. Такое разделение позволяет упростить расчеты, поскольку не требует явного решения для всех степеней свободы УФ-мод, а их влияние учитывается через стохастические силы, действующие на ИК-моды.
Для описания эволюции длинноволновых (IR) мод используются уравнения Ланжевена, включающие стохастические шумовые члены. Эти шумовые члены представляют собой влияние коротковолновых (UV) мод на динамику IR-мод. Математически, шум в уравнении Ланжевена моделируется как случайная сила, корреляционная функция которой связана с температурой и диссипацией UV-мод. Такой подход позволяет эффективно учитывать влияние высокоэнергетических степеней свободы на низкоэнергетическую динамику, не требуя явного решения для UV-мод, что существенно упрощает расчеты и позволяет моделировать системы с большим количеством степеней свободы. Интенсивность шумового члена пропорциональна температуре и коэффициенту диссипации, отражая термодинамическое равновесие между IR и UV модами.
Разделение длинноволновых (ИК) и коротковолновых (УФ) мод имеет принципиальное значение, поскольку позволяет моделировать влияние высокоэнергетических процессов на низкоэнергетическую динамику без необходимости явного решения уравнений для УФ-степеней свободы. Вместо этого, влияние УФ-мод аппроксимируется стохастическими членами в уравнениях Ланжевена, описывающих эволюцию ИК-мод. Такой подход значительно упрощает вычислительную сложность задачи, позволяя исследовать динамику системы в ИК-области, учитывая при этом эффект обратной связи от высокоэнергетических процессов, без детального знания или явного моделирования УФ-спектра. Это особенно важно в случаях, когда точное решение для УФ-мод является недоступным или вычислительно непрактичным.
Численное Моделирование: Укрощение Стохастического Хаоса
Для численного решения уравнений Ланжевена используются методы, разработанные для стохастических дифференциальных уравнений, такие как метод Эйлера-Маруямы и методы Рунге-Кутты. В данной реализации достигнута точность около 1%, что обусловлено дискретизацией и выбранным методом численного интегрирования. Метод Эйлера-Маруямы, являясь наиболее простым, имеет порядок точности O(\Delta t^{1/2}), где \Delta t — шаг по времени. Методы Рунге-Кутты более высокого порядка позволяют снизить погрешность, однако требуют больших вычислительных затрат. Ограничение в 1% связано с компромиссом между точностью и эффективностью вычислений, а также с влиянием ошибок округления при выполнении операций с числами с плавающей точкой.
Немарковскость, проявляющаяся в зависимости будущего состояния системы от всей её прошлой истории, представляет собой существенную сложность при численном решении стохастических уравнений. В отличие от марковских процессов, где будущее определяется только текущим состоянием, немарковские системы требуют учета корреляций во времени, что влечет за собой необходимость использования специализированных схем временной интеграции. Стандартные методы, такие как метод Эйлера-Маруямы или Рунге-Кутты, могут оказаться недостаточно точными или стабильными при наличии сильной немарковской памяти. Выбор оптимальной схемы интегрирования, учитывающей характер и масштаб немарковских эффектов, критически важен для получения корректных и надежных результатов моделирования. Это может потребовать использования более сложных методов, например, с учетом истории или адаптивных схем, изменяющих шаг интегрирования в зависимости от эволюции системы.
Стохастический формализм, используемый для описания открытых квантовых систем, подкрепляется формализмом интегралов по траекториям Швингера-Кельдыша. Данный подход позволяет последовательно учитывать флуктуации и диссипацию, возникающие из-за взаимодействия системы с окружающей средой. В рамках этого формализма, вычисляются корреляционные функции и другие физические величины, учитывая как причинные, так и антипричинные траектории, что необходимо для корректного описания немарковских эффектов и получения точных результатов. Математически, это достигается путем интегрирования по двум независимым копиям поля, каждая из которых соответствует одному направлению времени, что приводит к дублированию степеней свободы и требует специфических методов регуляризации и перенормировки для устранения расходимостей.
От Инфлятонного Потенциала к Первичным Черным Дырам: Следствие Квантовой Нестабильности
Потенциал скалярного поля V(ϕ), управляющий инфлатонным полем, играет ключевую роль в определении характеристик возникающих возмущений и возможности формирования первичных чёрных дыр. Форма этого потенциала непосредственно влияет на спектр флуктуаций плотности, которые, в свою очередь, определяют амплитуду и масштаб возмущений. Определённые формы потенциала, характеризующиеся крутыми склонами или специфическими особенностями, могут приводить к усилению возмущений на определённых масштабах, создавая условия для гравитационного коллапса и формирования первичных чёрных дыр. Более того, характеристики потенциала V(ϕ) влияют на спектральные свойства гравитационных волн, генерируемых в ранней Вселенной, предоставляя возможность косвенного исследования свойств инфлатонного поля и потенциала, определяющего эволюцию ранней Вселенной.
Формализм δN-δN представляет собой мощный инструмент для расчета флуктуаций кривизны, возникающих в ранней Вселенной, и оценки условий, необходимых для формирования примордиальных черных дыр. В его основе лежит идея, что кривизна пространства-времени тесно связана с локальными изменениями количества инфлатонных э-пох. Этот метод позволяет анализировать, как малые флуктуации плотности в начальный момент времени могут расти и коллапсировать под действием гравитации, формируя черные дыры. Особенно важно, что δN-δN не требует знания точной формы потенциала инфлатонного поля V(ϕ), а оперирует с изменениями числа э-пох, что делает его применимым к широкому классу инфляционных моделей. В результате, данный формализм позволяет установить связь между параметрами инфляционного потенциала и вероятностью образования примордиальных черных дыр, что критически важно для понимания их возможного вклада в темную материю и гравитационные волны.
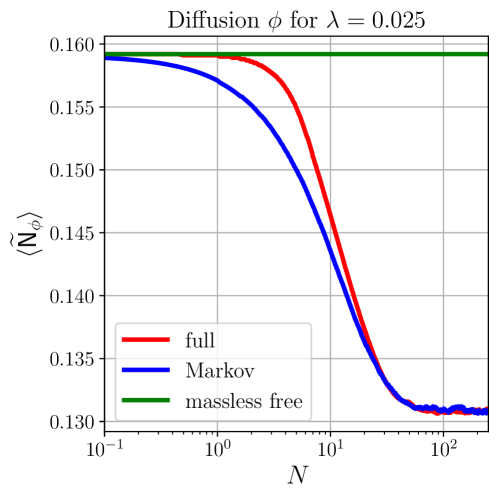
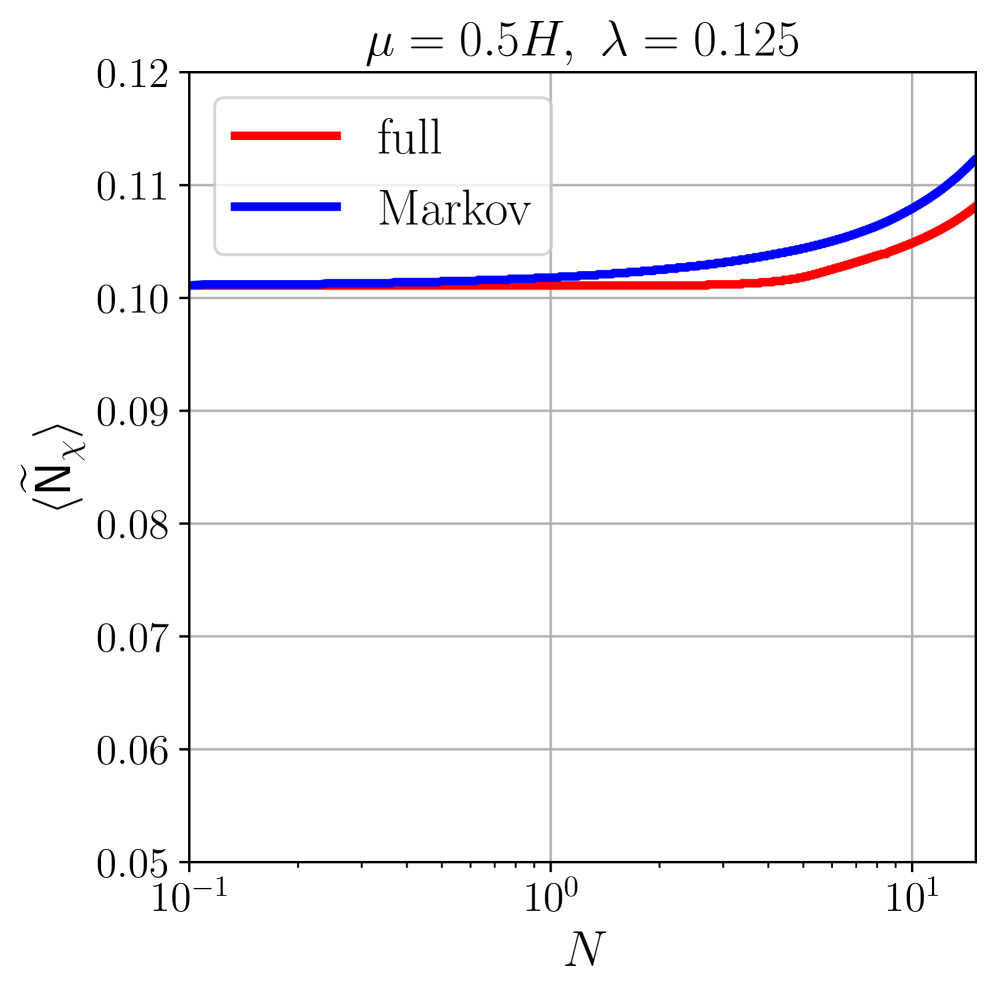
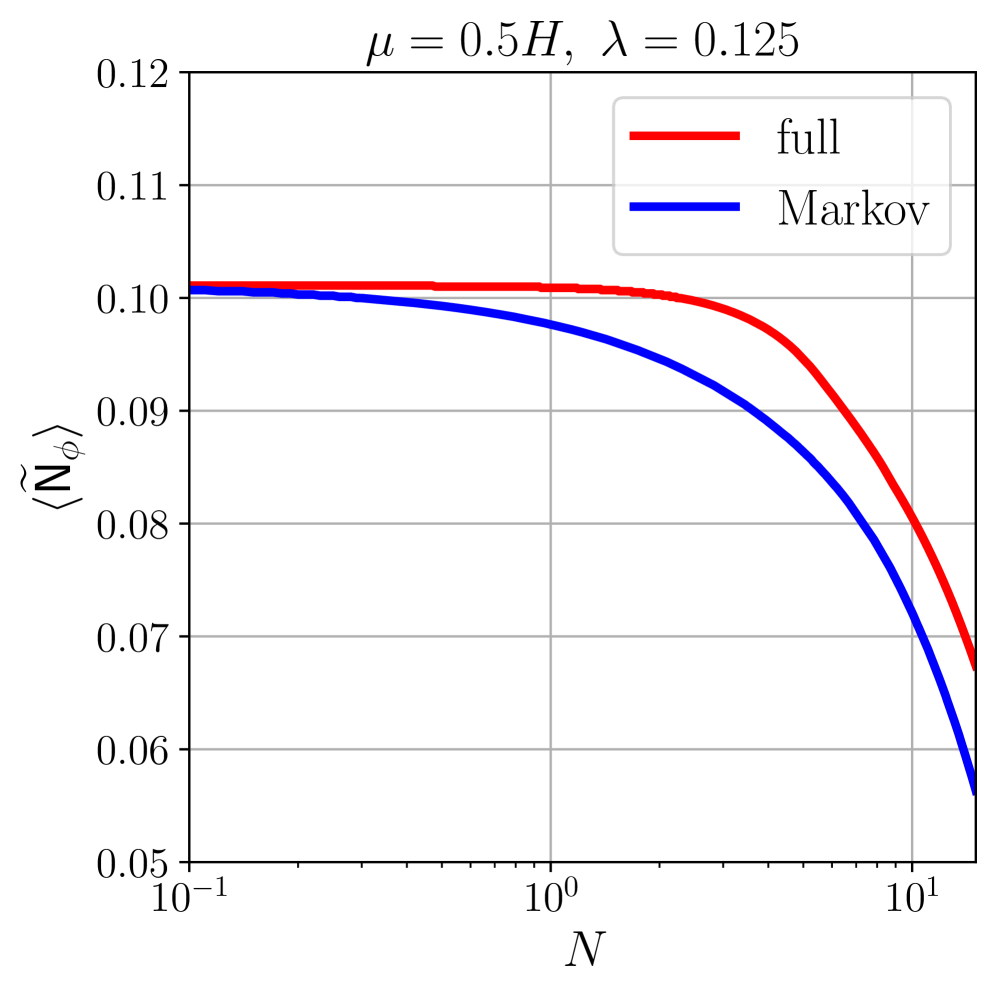
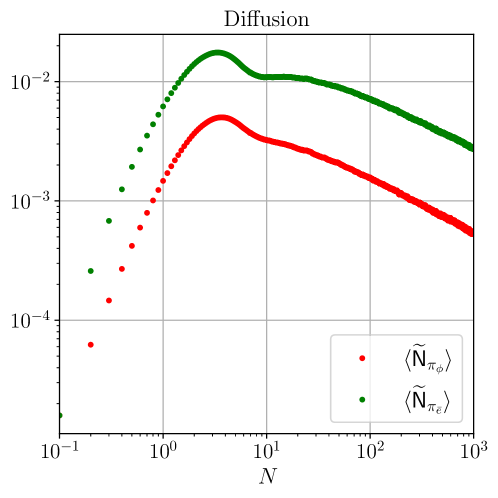
Стохастический формализм позволяет исследовать возникновение гравитационных волн, индуцированных скалярными флуктуациями. Данный подход подчеркивает значимость учета эффективных масс при анализе ранней Вселенной. Наблюдаемый рост дисперсии в направлении плоского поля ϕ служит прямым доказательством этого утверждения. Количественные различия в амплитудах диффузии указывают на то, что пренебрежение эффективными массами может приводить к существенным погрешностям в оценке характеристик гравитационных волн. Таким образом, точное моделирование генерации этих волн требует тщательного учета динамики скалярного поля и ее влияния на метрику пространства-времени.
Вектор Будущих Исследований: От Квантового Вакуума к Пониманию Ранней Вселенной
Стохастический формализм, применяемый в контексте пространства Де Ситтера и расширения, определяемого масштабом Хаббла, представляет собой надежную основу для изучения различных моделей инфляции. Этот подход позволяет рассматривать квантовые флуктуации как случайные поля, эволюционирующие во времени и пространстве, что особенно важно для понимания самых ранних стадий Вселенной. В рамках этого формализма, инфляционное расширение рассматривается не как детерминированный процесс, а как статистическая сумма множества возможных траекторий, каждая из которых соответствует определенной реализации случайного поля. Такой подход позволяет исследовать широкий спектр потенциалов V(ϕ) и, как следствие, различные сценарии инфляции, включая модели медленного разгона и новые инфляционные модели. Надежность этого метода подтверждается его способностью предсказывать спектральные характеристики возмущений, которые могут быть проверены с помощью космологических наблюдений.
Потенциал Минимальной Суперсимметричной Стандартной Модели (MSSM), обозначаемый как V(ϕ), служит конкретным примером, который может быть исследован в рамках установленной формальной теории случайных процессов. Этот потенциал описывает энергию скалярного поля ϕ и играет ключевую роль в моделировании инфляционной эпохи ранней Вселенной. Тщательный анализ формы этого потенциала позволяет получить предсказания относительно спектральных характеристик первичных гравитационных волн и флуктуаций плотности, которые могут быть обнаружены современными и будущими астрофизическими наблюдениями. В частности, параметры потенциала MSSM напрямую влияют на амплитуду и спектральный индекс этих флуктуаций, предоставляя возможность для проверки и уточнения моделей инфляции и, в конечном итоге, для понимания начальных условий, сформировавших наблюдаемую Вселенную.
Тщательный анализ начальных условий, в частности, использование вакуума Банча-Дэвиса для ультрафиолетовых мод, открывает новые возможности для понимания квантового происхождения Вселенной. Этот подход позволяет исследовать флуктуации квантового поля в ранние моменты времени, непосредственно влияющие на формирование крупномасштабной структуры. Усовершенствование численных методов, необходимых для решения сложных уравнений квантовой космологии, позволяет с высокой точностью моделировать эволюцию Вселенной от самых ранних стадий и, как следствие, предсказывать наблюдаемые характеристики реликтового излучения и распределения галактик. Таким образом, комбинация теоретических разработок и прогресса в вычислительных технологиях позволяет приблизиться к пониманию фундаментальных процессов, происходивших в первые моменты существования Вселенной, и проверить различные космологические модели.
Исследование, представленное в данной работе, демонстрирует, что стандартные упрощения, используемые в описании космологической инфляции, могут приводить к существенным погрешностям. В частности, пренебрежение немарковскими эффектами и неточная обработка эффективных масс полей приводят к искажению картины эволюции возмущений. Как отмечал Вильгельм Рентген: «Я не знаю, что это такое, но это, безусловно, что-то новое». Подобное высказывание отражает суть научного поиска: каждая, казалось бы, устоявшаяся теория, подобно горизонту событий, может скрывать за собой неизведанное, требующее пересмотра фундаментальных представлений. Данная работа, фокусируясь на численном моделировании стохастического формализма, указывает на необходимость более глубокого понимания влияния ультрафиолетовых мод и немарковских эффектов для построения адекватной картины ранней Вселенной.
Что же дальше?
Представленное исследование, используя численные методы, демонстрирует значимость немарковских эффектов в ранней Вселенной. Однако, стоит помнить, что текущие теории квантовой гравитации лишь предполагают, что горизонт событий может радикально изменить структуру пространства-времени. Реальность, возможно, гораздо сложнее и ускользает от простых моделей. Точность численного решения, хоть и впечатляет, всё же ограничена вычислительными ресурсами и допущениями, сделанными при моделировании ультрафиолетовых мод.
В дальнейшем необходимо сосредоточиться на разработке более совершенных методов учёта обратной связи между длинноволновыми и коротковолновыми модами, а также на исследовании влияния нелинейных эффектов. Важно понимать, что любое приближение, которое мы используем, может оказаться лишь иллюзией, скрывающей истинную природу инфляции. Необходимо искать способы проверки предсказаний теории, даже если это потребует принципиально новых экспериментальных установок.
В конечном счёте, изучение ранней Вселенной — это не только поиск ответов, но и осознание границ нашего знания. Каждая новая теория — это лишь временная модель, которая, подобно любому объекту, может исчезнуть за горизонтом событий нашей неполной информации. Истина, возможно, навсегда останется за пределами нашего понимания.
Оригинал статьи: https://arxiv.org/pdf/2602.11652.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Решение головоломки с паролем Absolum в Yeldrim.
- Прогнозы криптовалюты AXS: информация о ценах на AXS
- Откровенные заметки, слитые стримером Lacari, привели к его бану на Twitch и Kick.
- Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip
- The Planet Crafter: полное руководство по картам и биомам
- YAPYAP Список заклинаний
- 15 лучших законченных серий манхвы, которые стоит прочитать, в рейтинге
- Все рецепты культистского круга в Escape from Tarkov
- Как играть в REANIMAL в кооперативе с помощью Friend’s Pass (локальный и онлайн кроссплей)
- Все коды в Poppy Playtime Глава 4
2026-02-15 12:53