Информационный парадокс чёрных дыр: обратная сторона медали

Автор: Денис Аветисян

Новое исследование предлагает свежий взгляд на проблему сохранения информации при испарении чёрных дыр, рассматривая различные способы грубого зернирования квантовых состояний.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал

В рамках микроканонического гильбертова пространства, представленного в виде цепочки, эволюция состояния от полностью сформированной чёрной дыры, содержащей всю энергию, через последовательно испаряющиеся подпространства с уменьшением энергии чёрной дыры на каждом шаге <span class="katex-eq" data-katex-display="false">\approx E-n</span>, завершается в подпространстве полностью испарившейся чёрной дыры, характеризующемся максимальной энтропией, обусловленной экспоненциальным ростом числа состояний излучения с увеличением <span class="katex-eq" data-katex-display="false">n</span>. — В рамках микроканонического гильбертова пространства, представленного в виде цепочки, эволюция состояния от полностью сформированной чёрной дыры, содержащей всю энергию, через последовательно испаряющиеся подпространства с уменьшением энергии чёрной дыры на каждом шаге $\approx E-n$ , завершается в подпространстве полностью испарившейся чёрной дыры, характеризующемся максимальной энтропией, обусловленной экспоненциальным ростом числа состояний излучения с увеличением $n$ .

Работа посвящена анализу связи между ансамблевым усреднением, квантическим хаосом и микроканоническим ансамблем в контексте соответствия AdS/CFT.

Противоречие между унитарностью квантовой механики и полуклассическим описанием испарения черных дыр остается одной из ключевых проблем современной теоретической физики. В работе, озаглавленной ‘A Reverse Black Hole Information Problem’, исследуется возможность согласования этих двух подходов в рамках дуальности AdS/CFT, путем анализа различных процедур грубого зернирования (coarse-graining). Показано, что применение специфических методов усреднения к граничным состояниям CFT позволяет получить смешанные состояния, согласующиеся с излучением Хокинга, и прояснить связь между ансамблевым усреднением и точной унитарной динамикой. Не приведет ли более глубокое понимание процедур грубого зернирования к разрешению парадокса потери информации в черных дырах и к новой интерпретации квантовой гравитации?

За гранью горизонта событий: Введение в парадокс информации

Исчезновение черных дыр посредством излучения Хокинга представляет собой серьезную проблему для фундаментальных принципов квантовой механики. Согласно теории, черная дыра постепенно теряет массу, испуская частицы, но этот процесс, как представляется, уничтожает информацию о материи, которая когда-либо попала внутрь. Это противоречит принципу унитарности, согласно которому квантовая эволюция должна быть обратимой, и информация не может быть безвозвратно потеряна. Если информация действительно исчезает в черной дыре, это означало бы, что законы квантовой механики нуждаются в пересмотре или, по крайней мере, в существенном дополнении. Этот парадокс, известный как информационный парадокс черных дыр, является одним из самых глубоких и сложных вопросов современной теоретической физики, стимулируя активные исследования в области квантовой гравитации и теории струн.

Парадокс, возникающий вокруг черных дыр и потери информации, ставит под сомнение фундаментальный принцип квантовой механики — унитарную динамику. Унитарность предполагает, что эволюция квантовой системы полностью детерминирована и обратима, то есть, теоретически, возможно восстановить начальное состояние системы из любого конечного состояния. Однако, если информация, попавшая в черную дыру, действительно исчезает при испарении Хокинга, это нарушает унитарность, поскольку становится невозможно однозначно восстановить исходное состояние системы. Это противоречие представляет серьезную проблему для современной физики, поскольку унитарная динамика является краеугольным камнем всей квантовой теории, и ее нарушение может потребовать пересмотра основных принципов понимания эволюции квантовых систем и природы информации во Вселенной.

Полуклассическая AdS-гравитация представляет собой мощный теоретический инструмент для изучения парадокса информационного исчезновения в чёрных дырах. Эта концепция устанавливает глубокую связь между гравитацией в пространстве с большей размерностью (bulk) и квантовой теорией поля, существующей на его границе (boundary). В рамках этой дуальности, процессы, происходящие внутри чёрной дыры, могут быть описаны через квантово-механические явления на границе, что позволяет обойти некоторые проблемы, связанные с традиционным описанием гравитации вблизи сингулярностей. Таким образом, AdS-гравитация предоставляет уникальную возможность исследовать судьбу информации, падающей в чёрную дыру, и потенциально разрешить противоречие между общей теорией относительности и квантовой механикой, предлагая альтернативный взгляд на природу пространства-времени и информационного содержания Вселенной. $AdS$ пространство, в частности, обеспечивает благоприятную среду для изучения этих явлений благодаря своим специфическим геометрическим свойствам.

В рамках полуклассической AdS-гравитации, создание небольшой нестабильной чёрной дыры из чистого начального состояния, например, при коллапсе звезды или столкновении частиц, связано с квантовой теорией поля на границе пространства, что отражается в кривой энтропии состояния за горизонтом событий.

Запутанность как ключ к пониманию: Доказательства из квантовой механики

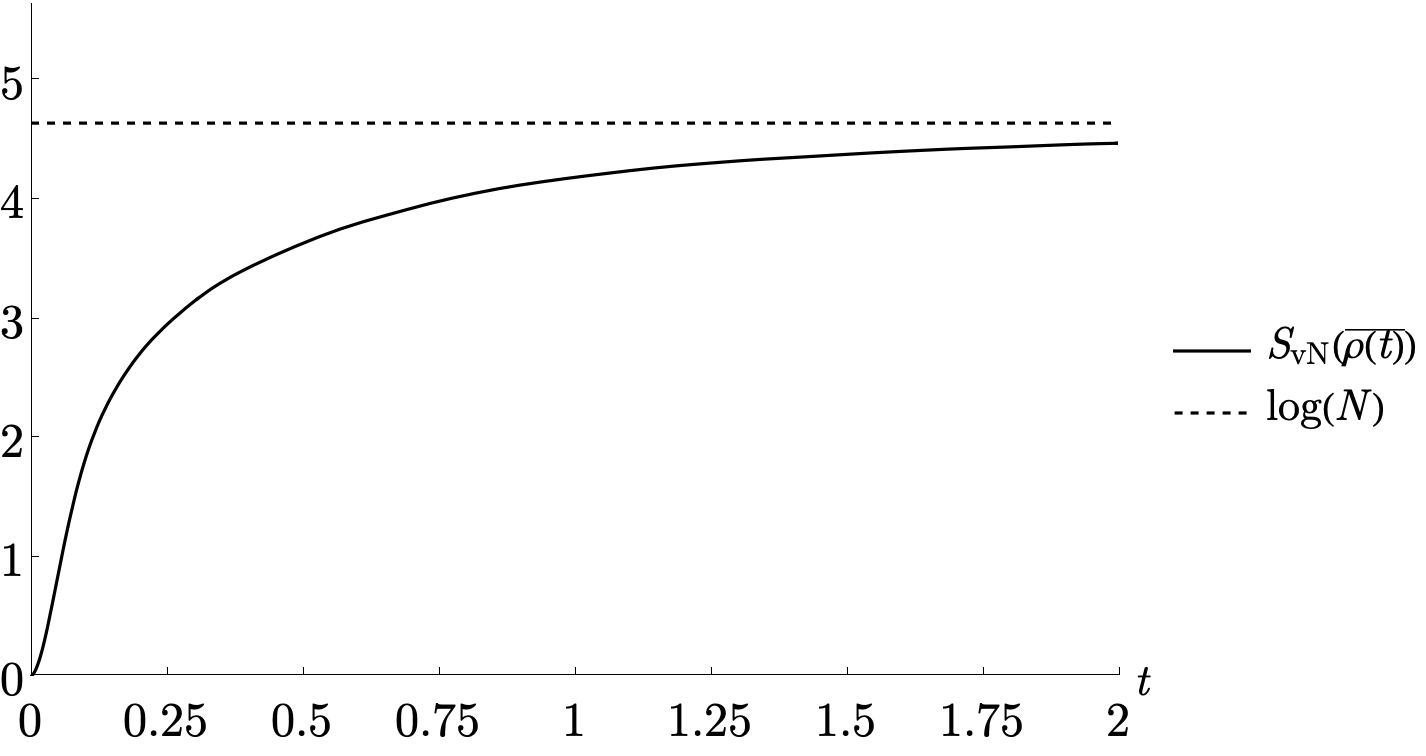
Энтропия фон Неймана, являющаяся мерой запутанности, играет ключевую роль в понимании того, как информация кодируется в пространстве-времени. В квантовой механике, запутанность возникает, когда две или более частиц связаны таким образом, что их квантовые состояния коррелируют, даже при разделении на значительные расстояния. $S(ρ) = -Tr(ρlog_2ρ)$ — это математическое выражение энтропии фон Неймана для матрицы плотности ρ, описывающей состояние квантовой системы. Высокое значение энтропии указывает на сильную запутанность и, следовательно, на большее количество информации, закодированной в корреляциях между квантовыми степенями свободы. В контексте гравитации, особенно в теории AdS/CFT, энтропия фон Неймана используется для изучения степени запутанности в граничной конформной теории поля, которая связана с геометрией пространства-времени в объеме AdS. Изменение энтропии фон Неймана может быть связано с изменениями в геометрии, например, с образованием или увеличением площади черной дыры, что указывает на то, что информация о микросостояниях черной дыры закодирована в запутанности.

Упрощение сложных систем посредством грубого зерна (coarse-graining) является ключевой методикой при применении полуклассической AdS-гравитации. Недавние исследования установили прямую связь между процедурами грубого зерна и возникновением полуклассического поведения в рамках данной теории. Этот подход позволяет эффективно оперировать с бесконечно сложными системами, выделяя существенные характеристики и игнорируя несущественные детали. В частности, применение грубого зерна позволяет описывать динамику черных дыр и решать проблему потери информации, связывая микроскопическое состояние системы с макроскопическими параметрами горизонта событий. Результаты показывают, что специфические процедуры грубого зерна воспроизводят полуклассическую гравитацию, обеспечивая согласованное описание физической реальности.

Измерение чистоты сглаженного состояния, выражаемое как $Tr(\bar{\rho}^2)$ , демонстрирует чувствительность к чистоте исходного состояния. Наблюдается снижение этого показателя на временной шкале, соответствующей формированию горизонта событий чёрной дыры. Данный факт указывает на потенциальную возможность сохранения информации, поскольку уменьшение чистоты сглаженного состояния связано с изменением энтропии и может отражать сохранение квантовой информации, избегая парадокса потери информации в чёрных дырах. Изменения $Tr(\bar{\rho}^2)$ служат индикатором динамики системы и коррелируют с процессами, происходящими на горизонте событий.

Вычисление фон Неймановской энтропии усредненной матрицы плотности <span class="katex-eq" data-katex-display="false">\overline{\rho_{\scriptscriptstyle\mathrm{BH}}(t)}</span> показывает, что средняя энтропия <span class="katex-eq" data-katex-display="false">\overline{S_{\rm vN}(\rho_{\scriptscriptstyle\mathrm{BH}}(t))}</span> при заданных параметрах (<span class="katex-eq" data-katex-display="false">\sigma = 10/\sqrt{2}</span>) и усреднении по 1000 реализациям <span class="katex-eq" data-katex-display="false">H_{\scriptscriptstyle\mathrm{mix,BH}}^{(E-n)}</span> равна нулю, несмотря на учет единственной реализации <span class="katex-eq" data-katex-display="false">H_{\scriptscriptstyle\mathrm{hop}}</span> и <span class="katex-eq" data-katex-display="false">H_{\scriptscriptstyle\mathrm{mix,rad}}^{(n)}</span>. — Вычисление фон Неймановской энтропии усредненной матрицы плотности $\overline{\rho_{\scriptscriptstyle\mathrm{BH}}(t)}$ показывает, что средняя энтропия $\overline{S_{\rm vN}(\rho_{\scriptscriptstyle\mathrm{BH}}(t))}$ при заданных параметрах ( $\sigma = 10/\sqrt{2}$ ) и усреднении по 1000 реализациям $H_{\scriptscriptstyle\mathrm{mix,BH}}^{(E-n)}$ равна нулю, несмотря на учет единственной реализации $H_{\scriptscriptstyle\mathrm{hop}}$ и $H_{\scriptscriptstyle\mathrm{mix,rad}}^{(n)}$ .

Граничные соответствия и решение голографической головоломки

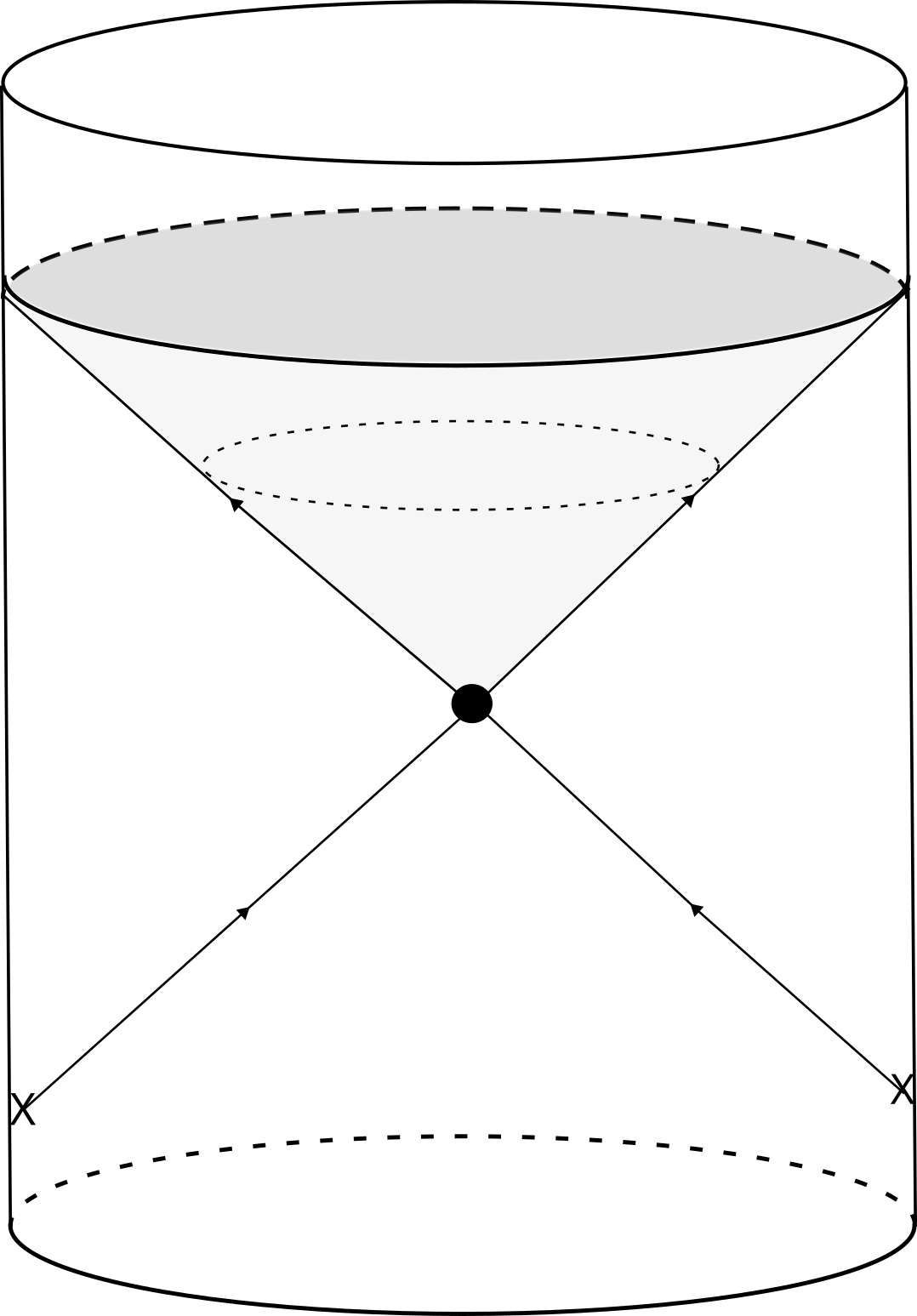
Граничные условия пространства AdS описываются граничной конформной теорией поля (CFT), где информация о гравитационном объеме кодируется в корреляциях между операторами. Данная корреспонденция AdS/CFT устанавливает эквивалентность между теорией гравитации в $D+1$ -мерном пространстве Анти-де Ситтера и конформной теорией поля в $D$ -мерном пространстве на границе. Корреляционные функции в CFT напрямую связаны с геометрией и динамикой в bulk, позволяя реконструировать гравитационные свойства пространства AdS из наблюдаемых величин в граничной теории. В частности, n-точечные корреляционные функции операторов соответствуют геодезическим в bulk, а их поведение при различных значениях параметров определяет свойства гравитационного поля.

Двухточечные корреляционные функции в конформной теории поля (КТП) на границе пространства AdS предоставляют ключевую информацию о структуре теории и поведении материи. Анализ этих функций позволяет исследовать фазовые переходы, в частности, переходы между фазами конфайнмента и деконфайнмента. Изменения в поведении корреляционных функций при приближении к критической точке фазового перехода отражают изменения в степенях свободы системы и характер спонтанного нарушения симметрии. В частности, поведение корреляционных функций в пределе малых расстояний связано с краткодействующими сингулярностями операторов и может быть использовано для определения характеристических масштабов, определяющих физические свойства материи в различных фазах. Изучение этих функций в КТП на границе AdS обеспечивает важную связь между граничными и объемными степенями свободы, позволяя исследовать динамику черных дыр и другие гравитационные явления посредством анализа корреляций операторов на границе.

Коэффициенты OPE, характеризующие сингулярности операторов на малых расстояниях, являются ключевыми для восстановления динамики гравитационного фона из конформной полевой теории (CFT). В частности, времена смешивания состояний, определяемые параметрами, такими как σ и количеством гильбертовых подпространств $ℋ(n)$ , демонстрируют соответствие ожиданиям, полученным из анализа испарения черных дыр в гравитационном контексте. Это соответствие указывает на то, что информация о геометрии и динамике гравитационного пространства-времени кодируется в структуре сингулярностей операторов CFT и может быть реконструирована на основе анализа коэффициентов OPE и временных характеристик смешивания состояний.

Столкновение двух локализованных волновых пакетов частиц в пространстве AdS приводит к образованию нестабильной, кратковременной чёрной дыры, излучение которой проявляется в виде сферической оболочки (серый конус).

За пределами привычного: Многограничные червоточины и будущее исследований

Многограничные червоточины, представляющие собой гипотетические туннели, соединяющие различные области пространства-времени, рассматриваются как ключевой механизм сохранения квантовой запутанности в сложных системах. Предполагается, что эти структуры обеспечивают своего рода «короткие пути» для корреляций между удаленными частями системы, предотвращая их разрушение из-за декогеренции. В частности, в сценариях, где существует несколько границ, разделяющих различные фазы или подсистемы, многограничные червоточины могут выступать в роли посредников, позволяя информации о запутанности распространяться между ними. Это особенно важно для понимания поведения систем с высокой степенью запутанности, таких как черные дыры или квантовые вычисления, где сохранение корреляций является фундаментальным требованием для функционирования. Исследование этих структур позволяет надеяться на более глубокое понимание связи между геометрией пространства-времени и квантовой информацией.

Проблема факторизации возникает при исследовании корреляционных функций в системах с множественными границами, представляя собой серьезную задачу для понимания голографической запутанности. В частности, наблюдается, что поведение этих функций отклоняется от ожидаемого при наличии нескольких границ, что указывает на необходимость более глубокого анализа взаимосвязи между запутанностью на границе и геометрией в объеме. Это отклонение требует пересмотра стандартных представлений о том, как информация кодируется и сохраняется в голографических системах, а также поиска новых методов для описания корреляций в сложных многограничных конфигурациях. Понимание данной проблемы имеет ключевое значение для построения непротиворечивой теории квантовой гравитации и объяснения сохранения информации в черных дырах, поскольку голографический принцип предполагает эквивалентность между гравитационной системой в объеме и квантовой теорией поля на ее границе.

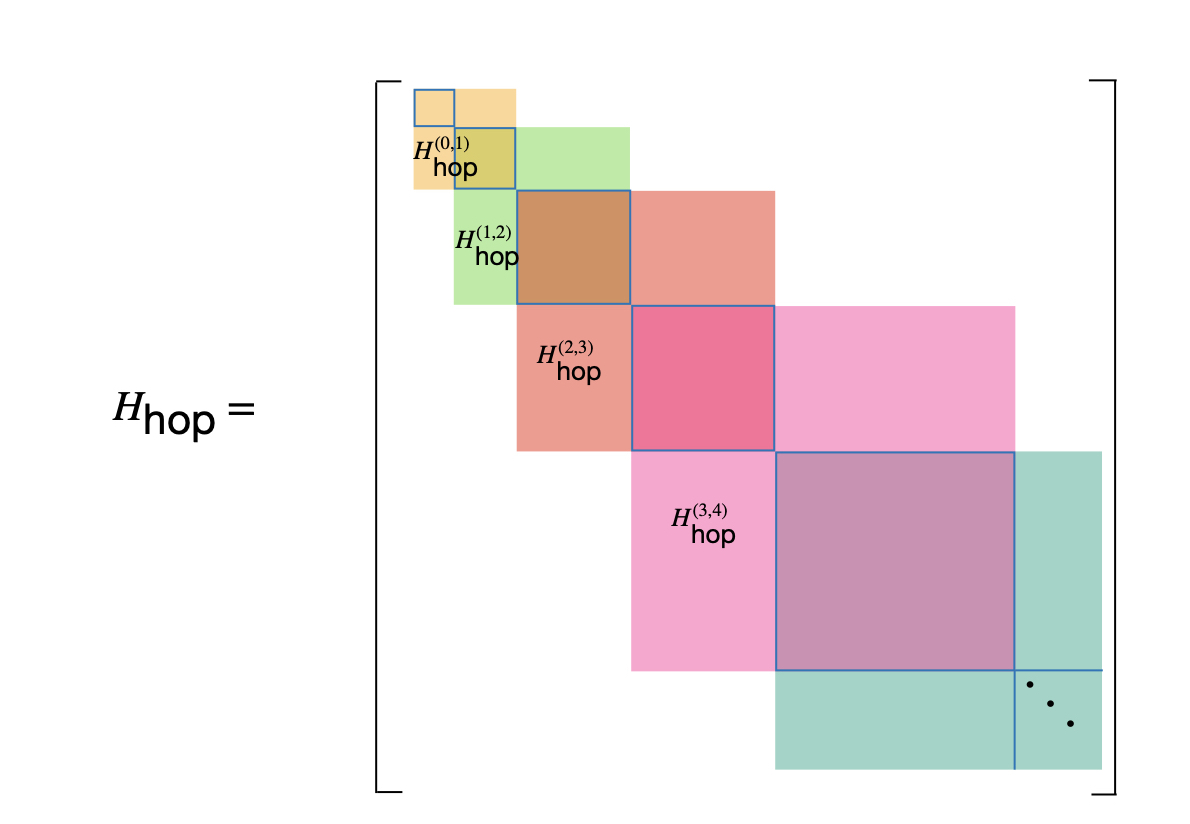
В вычислениях энтропии запутанности возникают репликационные червоточины, представляющие собой потенциальный путь к решению так называемой «факторизационной головоломки» и пониманию сохранения информации в сложных квантовых системах. Эти виртуальные червоточины, проявляющиеся в математических моделях, позволяют исследовать взаимосвязь между корреляциями на границе и геометрией в объеме. Для количественной оценки хаотичности системы и установления корреляции между пограничным и объемным поведением используется спектральный фактор формы $g(t) = |\text{Tr}(PH e^{(iHt)})/\text{Tr}(PH)|²$ , где $P$ — проектор на основное пространство, $H$ — гамильтониан системы, а $t$ — время. Анализ этого фактора позволяет предположить, что хаотичность в граничной теории соответствует сложной геометрии в объеме, что может объяснить, как информация сохраняется даже при прохождении через червоточины.

Гамильтониан скачков <span class="katex-eq" data-katex-display="false">H_{hop}</span> формируется из множества перекрывающихся гамильтонианов <span class="katex-eq" data-katex-display="false">H_{hop}^{(n,n+1)}</span>, описывающих излучение и поглощение квантов Хокинга, действующих в гильбертовых подпространствах размерности <span class="katex-eq" data-katex-display="false">N^{(n)} \times N^{(n)}</span>, и каждый такой гамильтониан <span class="katex-eq" data-katex-display="false">H_{hop}^{(n,n+1)}</span> имеет размерность <span class="katex-eq" data-katex-display="false">(N^{(n)}+N^{(n+1)})^{2}</span>, представляя собой случайную величину из унитарного ансамбля со средним нулем и дисперсией <span class="katex-eq" data-katex-display="false">2\sigma^{2}</span>. — Гамильтониан скачков $H_{hop}$ формируется из множества перекрывающихся гамильтонианов $H_{hop}^{(n,n+1)}$ , описывающих излучение и поглощение квантов Хокинга, действующих в гильбертовых подпространствах размерности $N^{(n)} \times N^{(n)}$ , и каждый такой гамильтониан $H_{hop}^{(n,n+1)}$ имеет размерность $(N^{(n)}+N^{(n+1)})^{2}$ , представляя собой случайную величину из унитарного ансамбля со средним нулем и дисперсией $2\sigma^{2}$ .

Исследование, представленное в данной работе, затрагивает фундаментальные вопросы о природе информации и её сохранении в контексте гравитационного коллапса. Подобно тому, как художник стремится к гармонии в композиции, авторы стремятся согласовать квантовую механику с полуклассическим описанием испарения чёрных дыр, исследуя различные способы приближения к реальности. Фрэнсис Бэкон справедливо замечал: «Знание — сила». В данном случае, глубокое понимание механизмов, лежащих в основе излучения Хокинга и связанных с ним процессов грубого масштабирования, открывает путь к решению парадокса информации о чёрных дырах и укрепляет основы нашего понимания Вселенной. Усилия, направленные на согласование ансамблевого усреднения и микроканонического ансамбля, демонстрируют изысканный подход к сложной проблеме, где каждая деталь играет решающую роль.

Куда же это всё ведёт?

Исследование, представленное в данной работе, скорее обнажает глубину нерешенных вопросов, чем предлагает окончательные ответы. Попытки согласовать унитарность квантовой механики с кажущейся необратимостью испарения чёрных дыр через различные карты грубого приближения — элегантное упражнение, но не лишенное изящной иронии. Ведь само понятие «грубого приближения» подразумевает некую потерю информации, что и является источником парадокса. Остаётся ли эта потеря принципиальной, или же она является артефактом нашего неспособного к полной детализации описания?

В дальнейшем, необходимо более тщательно исследовать влияние различных ансамблевых усреднений на получаемые результаты. Сравнение микроканонического ансамбля с другими статистическими подходами, возможно, выявит скрытые предположения, определяющие нашу интерпретацию излучения Хокинга. Особенно важно понять, насколько универсальны полученные результаты для различных размерностей и типов чёрных дыр. Ведь элегантность теории проявляется не только в математической красоте, но и в её способности описывать разнообразие физической реальности.

В конечном итоге, разрешение парадокса информации о чёрных дырах, вероятно, потребует не просто усовершенствования существующих моделей, а принципиально нового взгляда на природу пространства-времени и квантовой гравитации. Истинное понимание, возможно, придёт не от поиска «правильной» карты грубого приближения, а от осознания того, что само понятие информации нуждается в пересмотре в контексте квантовой гравитации.

Оригинал статьи: https://arxiv.org/pdf/2601.22077.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-30 12:20