Искривление пространства: новый подход к гравитации «пчелы»

Автор: Денис Аветисян

---

В новой работе ученые предлагают оригинальный метод построения решений в теории гравитации «пчелы», основанный на использовании уравнения Гамильтона-Якоби и позволяющий описывать искривление пространства вокруг вращающихся черных дыр.

Разработана техника генерации точных решений для метрик Керра-Ньюмана-(A)dS в теории гравитации «пчелы» с использованием векторного поля, представляющего нарушение Лоренц-инвариантности.

Поиск точных решений в модифицированных теориях гравитации, таких как гравитация «bumblebee», часто сталкивается со значительными трудностями. В работе ‘Exact Kerr-Newman-(A)dS and other spacetimes in bumblebee gravity: employing a novel generating technique’ предложен новый метод построения точных решений, использующий уравнение Гамильтона-Якоби и векторное поле, описывающее нарушение Лоренц-инвариантности. Данный подход позволяет получить обобщения пространства-времени Керра-Ньюмана-(анти-)де Ситтера, зависящие от параметров геодезических. Каким образом предложенная техника может быть расширена для исследования других модификаций общей теории относительности и построения новых космологических моделей?

---

В поисках Новой Симметрии Вселенной

Несмотря на впечатляющий успех общей теории относительности в описании гравитации, научное сообщество предполагает, что она может быть лишь приближением к более фундаментальной теории. Эта гипотеза побуждает к поиску нарушений симметрии Лоренца — краеугольного камня современной физики, предписывающего одинаковость физических законов во всех инерциальных системах отсчета. Поиск таких нарушений — сложная задача, требующая разработки новых экспериментальных методик и теоретических моделей, способных выявить отклонения от предсказаний стандартной теории. Обнаружение даже малейших отклонений могло бы радикально изменить наше понимание гравитации, пространства и времени, открыв путь к новой эре в физике фундаментальных взаимодействий.

Теоретические построения, такие как теория струн и петлевая квантовая гравитация, независимо предсказывают нарушение Лоренц-инвариантности на фундаментальном уровне. В рамках этих моделей, пространство-время, которое в общей теории относительности представляется гладким и непрерывным, может обладать структурой, напоминающей дискретную или некоммутативную геометрию на планковских масштабах. Это приводит к тому, что скорость света не является абсолютной константой для всех частиц и энергий, а может слегка варьироваться в зависимости от их характеристик. Подобные нарушения симметрии, хотя и чрезвычайно малы, потенциально могут проявиться в виде аномалий в распространении космических лучей сверхвысоких энергий или в поляризации света от далеких астрономических объектов, открывая новые пути для проверки этих сложных теоретических конструкций и поиска более полной картины гравитации.

Поиск экспериментальных подтверждений нарушения лоренц-инвариантности требует разработки модифицированных теорий гравитации, способных предсказать и зарегистрировать отклонения от стандартной модели. Эти теории, выходящие за рамки общей теории относительности, исследуют возможность появления новых членов в уравнениях гравитации, которые проявляются при экстремальных энергиях или вблизи сингулярностей. Особое внимание уделяется разработке прецизионных экспериментов, использующих астрономические наблюдения, гравитационные волны и лабораторные измерения, для поиска крошечных эффектов, указывающих на нарушение фундаментальной симметрии пространства-времени. Успешное обнаружение таких отклонений не только подтвердит предсказания теоретической физики, но и откроет новые пути к пониманию природы гравитации и структуры Вселенной на самых фундаментальных уровнях.

Гравитация «Бамблби»: Новый Взгляд на Нарушение Симметрии

Теория гравитации «Бамблби» является расширением общей теории относительности, вводящим так называемое «поле Бамблби» — векторное поле, предназначенное для нарушения Лоренц-инвариантности. В отличие от стандартной модели, где Лоренц-инвариантность является фундаментальным принципом, данная теория постулирует наличие ненулевого вакуумного среднего значения для этого поля. Это нарушение симметрии предполагает, что физические законы могут отличаться в различных направлениях пространства-времени, что может проявляться в анизотропных гравитационных взаимодействиях и, потенциально, приводить к наблюдаемым эффектам, отличающимся от предсказаний общей теории относительности. Векторный характер поля Бамблби означает, что оно имеет величину и направление в каждой точке пространства-времени, что существенно отличает его от скалярных или тензорных полей, используемых в стандартных моделях гравитации.

Поле Бамблби характеризуется ненулевым вакуумным ожидаемым значением (Vacuum Expectation Value — VEV), которое играет ключевую роль в спонтанном нарушении Лоренц-инвариантности. В квантовой теории поля VEV представляет собой среднее значение поля в вакуумном состоянии. Ненулевое VEV поля Бамблби означает, что даже в отсутствии частиц поле имеет постоянную, отличную от нуля величину, что приводит к анизотропии в структуре вакуума и, как следствие, к модификации взаимодействия частиц с гравитацией. Величина VEV определяет степень нарушения симметрии и, следовательно, интенсивность эффектов, проявляющихся в гравитационном поле. < \Phi > \neq 0 , где Φ — поле Бамблби, указывает на наличие спонтанного нарушения симметрии.

Траектория поля “Бамблби” определяется геодезическими кривыми, что напрямую связывает его с геометрией пространства-времени. Геодезические представляют собой кратчайшие пути между двумя точками в искривленном пространстве-времени, и поле “Бамблби” следует этим путям, определяемым метрикой пространства-времени. Это означает, что эволюция поля не является произвольной, а диктуется геометрией окружающего пространства. \nabla_u u^v = 0 — уравнение геодезической, описывающее движение частицы вдоль кратчайшего пути, и аналогичное уравнение определяет эволюцию поля “Бамблби”. В контексте теории гравитации, геодезические кривые играют центральную роль в определении движения тел, и использование их для описания поля “Бамблби” подчеркивает интеграцию этого поля в структуру гравитационного взаимодействия.

Решение для Пространства-Времени: Формализм Гамильтона-Якоби

Уравнение Гамильтона-Якоби предоставляет эффективный метод получения решений в теории гравитации «bumblebee», исходя из заданных фоновых метрик. Этот подход позволяет вывести решения, характеризующиеся энергией (E), угловым моментом (L) и константой Картера (C). В частности, используя данное уравнение, можно описывать геодезические траектории частиц и света в искривленном пространстве-времени, определяя их движение через эти константы интегрирования. Решения, полученные с помощью уравнения Гамильтона-Якоби, являются аналитическими и позволяют исследовать свойства гравитационного поля в различных конфигурациях. H(q,p,t) = 0 является общей формой уравнения, где q — координаты, p — канонические импульсы, а H — гамильтониан системы.

Метод разделения переменных является ключевым инструментом для решения уравнения Гамильтона-Якоби, значительно упрощающим его математический аппарат. Данный подход предполагает разделение волновой функции или решения на независимые функции, каждая из которых зависит только от одного набора переменных. В контексте гравитации, это позволяет разложить сложную задачу на более простые, решаемые по отдельности, например, по радиальной и угловым координатам. Успешное применение разделения переменных приводит к существенному уменьшению размерности решаемых дифференциальных уравнений, делая получение аналитических решений более доступным, особенно для задач, описывающих геодезические линии и движение частиц в искривленном пространстве-времени. \psi(x,y,z) = X(x)Y(y)Z(z)

Пространство-время Керра-Ньюмена-Тауба-НУТ-AdS является ключевой отправной точкой для получения решений в теории гравитации, поскольку оно сочетает в себе несколько важных характеристик. Данное решение включает в себя вращение (a), электрический заряд (Q), массу (M), параметр Тауба-НУТ (l) и космологическую постоянную (Λ), что делает его чрезвычайно гибким для моделирования различных астрофизических сценариев. Использование этого решения в качестве исходного позволяет получать решения, описывающие геодезические траектории частиц и лучей света в сложных гравитационных полях, и служит основой для исследования влияния этих параметров на структуру пространства-времени.

Свойства Пространства-Времени и Теоретическое Обоснование

Пространство-время Керра-Ньюмена-Тауба-НУТ-AdS (KNTNA) представляет собой математическую модель, элегантно объединяющую в себе фундаментальные аспекты Вселенной. В отличие от более простых решений уравнений Эйнштейна, KNTNA изначально включает в себя как космологическую постоянную, отвечающую за ускоренное расширение пространства, так и электромагнитное поле. Это означает, что данная модель не требует добавления этих компонентов «вручную», как это часто делается в других теоретических построениях. Космологическая постоянная, обозначаемая обычно Λ, определяет скорость расширения Вселенной, в то время как электромагнитное поле описывает взаимодействие заряженных частиц. Естественная интеграция этих двух ключевых элементов в KNTNA делает её особенно привлекательной для изучения сложных астрофизических явлений, таких как вращающиеся чёрные дыры во Вселенной с ненулевой энергией вакуума и наличием электромагнитного излучения.

Для упрощения анализа сложной динамики, связанной с полем «бамблби», используется подход эффективной теории поля. Данный метод позволяет рассматривать данное поле не как фундаментальную составляющую структуры пространства-времени, а как внешнее воздействие на него. Это значительно облегчает математическое описание и позволяет сосредоточиться на наблюдаемых эффектах, возникающих под влиянием этого поля. Вместо попыток описать все взаимодействия на фундаментальном уровне, эффективная теория поля концентрируется на низкоэнергетических проявлениях, что делает возможным получение приближенных, но достаточно точных решений, применимых к конкретным физическим задачам. Такой подход широко используется в современной физике высоких энергий для изучения сложных систем, где точное решение уравнений невозможно или крайне затруднительно.

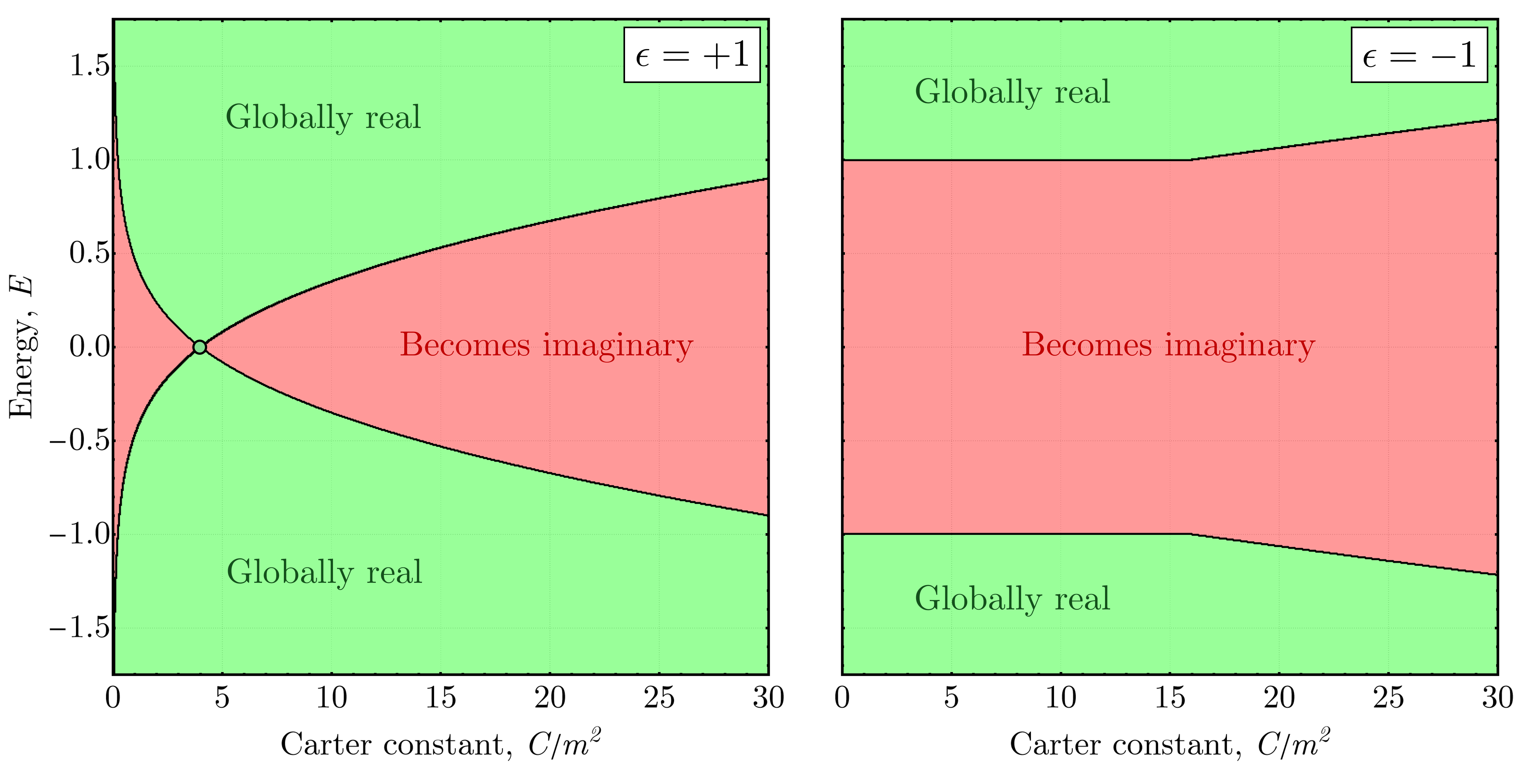
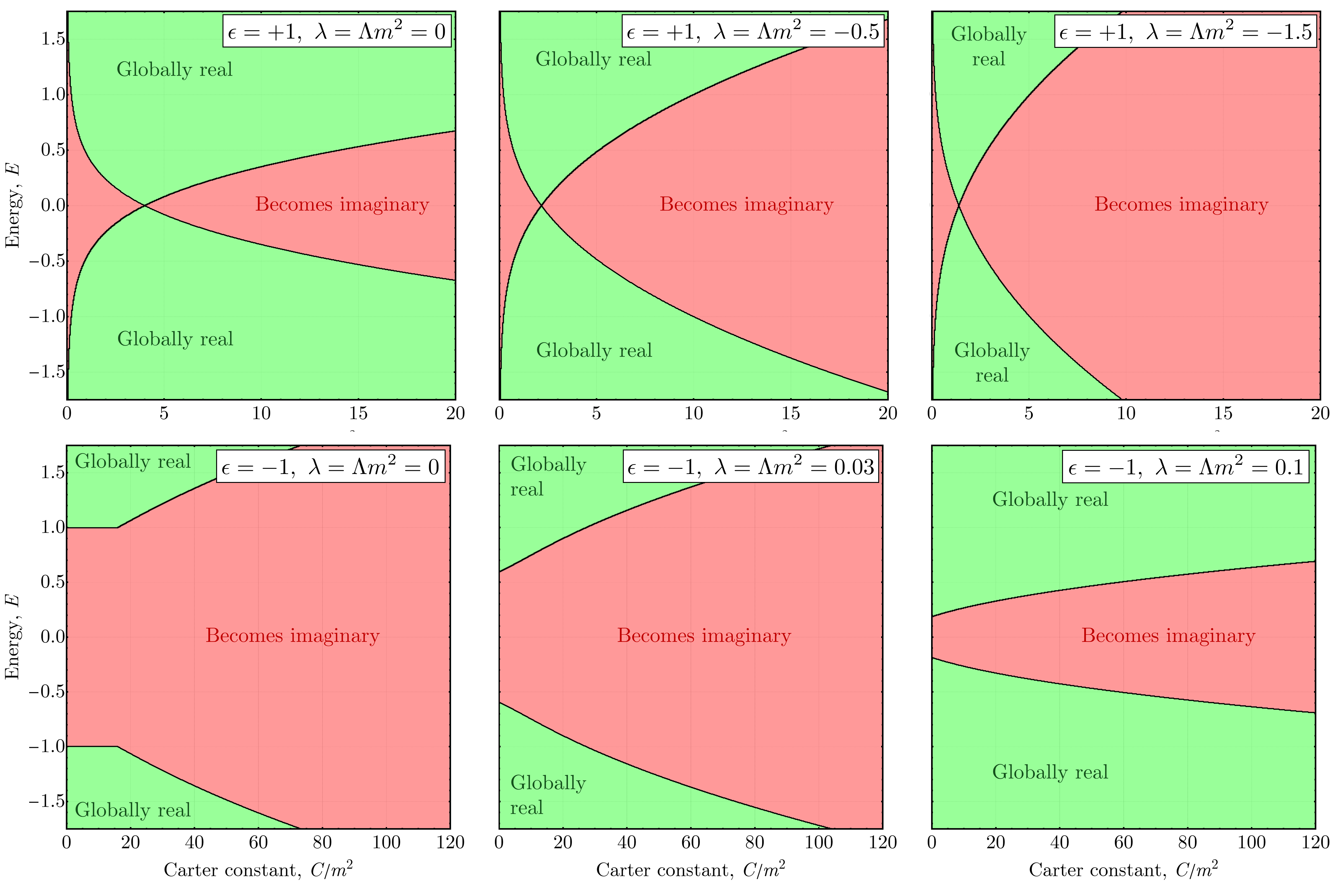
Стандартная модель расширений (Standard Model Extension, SME) предоставляет теоретическую основу для взаимодействия так называемого «шмелевого поля» с известными частицами, открывая перспективы для экспериментальной проверки его существования. Исследования показывают, что шмелевое поле приобретает глобальную реальность при определенных условиях, а именно, когда значение параметра L равно нулю и энергия (E) с константой Картера (C) находятся в конкретных диапазонах. Это взаимодействие предполагает возможность обнаружения влияния поля на свойства частиц, например, через небольшие отклонения от предсказаний стандартной модели в экспериментах с высокой точностью. В рамках SME разрабатываются конкретные сценарии, предсказывающие наблюдаемые эффекты, что делает данное поле потенциально верифицируемым элементом современной физики. L=0 является критическим условием для обеспечения глобальной реальности шмелевого поля.

Исследование, представленное в статье, демонстрирует, как математические инструменты — в данном случае, уравнение Гамильтона-Якоби и векторное поле, представляющее нарушение Лоренц-инвариантности — могут быть использованы для построения сложных моделей гравитации. Это напоминает о том, что любая формализация, любой алгоритм, не является нейтральным. Карл Поппер однажды сказал: «Неограниченное расширение познания без моральных ориентиров — это путь к катастрофе». Подобно тому, как векторное поле в статье определяет характеристики пространства-времени, так и ценности, заложенные в алгоритмы, определяют траекторию технологического прогресса. Игнорирование этических аспектов при разработке подобных моделей несёт ответственность перед обществом, ведь каждая математическая конструкция кодирует определенное мировоззрение.

Куда же это всё ведёт?

Представленная методика, позволяющая генерировать решения гравитации «шмеля» из фоновых пространств-времен, безусловно, расширяет инструментарий исследователя. Однако, за кажущейся элегантностью математических построений скрывается вопрос: что именно мы автоматизируем? Эффективность получения новых решений не должна заслонять необходимость критического осмысления физической интерпретации. Нахождение решений уравнения Гамильтона-Якоби — это лишь первый шаг; понимание того, как нарушение Лоренц-инвариантности влияет на наблюдаемые явления, требует гораздо более глубокого анализа.

Особого внимания заслуживает связь между параметрами, определяющими вектор нарушения Лоренц-инвариантности, и физическими характеристиками пространства-времени. Определение этих параметров из экспериментальных данных остаётся сложной задачей. Более того, необходимо учитывать, что вакуумное ожидаемое значение, определяющее силу нарушения, может зависеть от энергии и, следовательно, от масштаба рассматриваемых явлений. Прогресс без этики — это ускорение без направления; каждый алгоритм кодирует мировоззрение, и ответственность за автоматизируемые ценности лежит на исследователе.

В перспективе, данная методика может быть расширена для изучения более сложных гравитационных моделей и даже применена в контексте космологических исследований. Однако, важно помнить, что эффективность без морали — иллюзия. Поиск решений ради самих решений — занятие бесплодное. Необходимо сосредоточиться на решении реальных физических проблем и понимании фундаментальных принципов, лежащих в основе Вселенной.

---

Оригинал статьи: https://arxiv.org/pdf/2601.16037.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

• Все рецепты культистского круга в Escape from Tarkov

• Решение головоломки с паролем Absolum в Yeldrim.

• Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip

• Лучшие транспортные средства в Far Cry 6

• Лучшие шаблоны дивизий в Hearts Of Iron 4

• Где найти и поймать бабочку Солнечного луча в Палии

• Необходимо: Как выращивать урожай

• Dragon’s Dogma 2: Где найти Драконорожденных

• Как получить скины Alloyed Collective в Risk of Rain 2

• 15 лучших законченных серий манхвы, которые стоит прочитать, в рейтинге

2026-01-25 08:19