Колебания импульса и барионная плотность: новый взгляд на релятивистские столкновения

Автор: Денис Аветисян

Исследование флуктуаций среднего поперечного импульса и их зависимости от скорости позволяет глубже понять свойства плотной барионной среды, формирующейся в релятивистских тяжелых ионных столкновениях.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал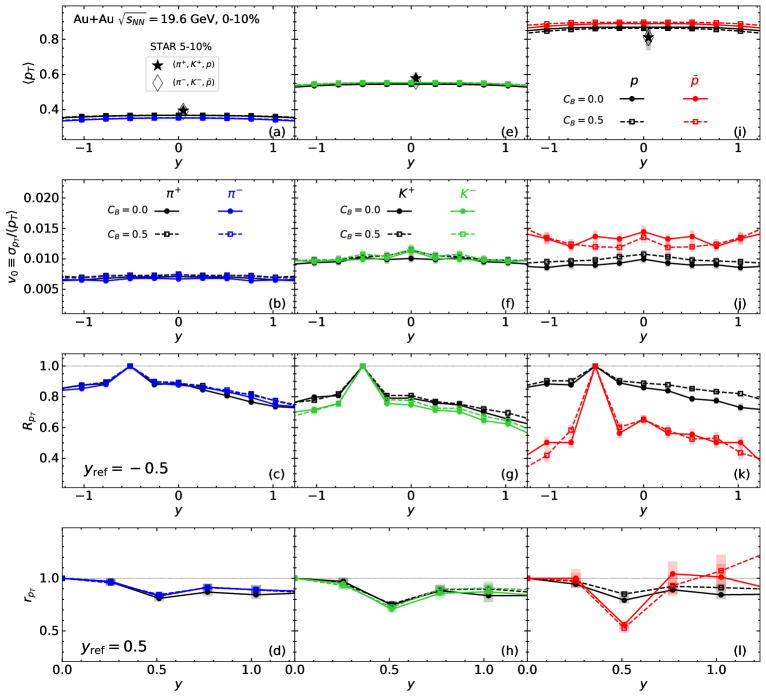

В ходе столкновений ионов золота при энергии <span class="katex-eq" data-katex-display="false">\sqrt{s\_{NN}}=19.6</span> ГэВ наблюдается зависимость характеристик поперечного импульса адронов (среднего значения, дисперсии, и коэффициентов корреляции) от псевдобыстроты, причём учет диффузии барионов (с параметрами <span class="katex-eq" data-katex-display="false">C\_B = 0.0</span> и <span class="katex-eq" data-katex-display="false">C\_B = 0.5</span>) вносит различия в наблюдаемые закономерности для <span class="katex-eq" data-katex-display="false">\pi^{\pm}</span>, <span class="katex-eq" data-katex-display="false">K^{\pm}</span> и протонов/антипротонов. — В ходе столкновений ионов золота при энергии $\sqrt{s\_{NN}}=19.6$ ГэВ наблюдается зависимость характеристик поперечного импульса адронов (среднего значения, дисперсии, и коэффициентов корреляции) от псевдобыстроты, причём учет диффузии барионов (с параметрами $C\_B = 0.0$ и $C\_B = 0.5$ ) вносит различия в наблюдаемые закономерности для $\pi^{\pm}$ , $K^{\pm}$ и протонов/антипротонов.

Работа посвящена изучению зависимости флуктуаций среднего поперечного импульса и их декореляции от скорости, как инструмента для исследования уравнения состояния и распределения барионной плотности в релятивистских тяжелых ионных столкновениях.

В релятивистских столкновениях тяжелых ионов установление свойств плотной барионной материи остается сложной задачей. В работе, озаглавленной ‘Rapidity dependence of mean transverse momentum fluctuation and decorrelation in baryon-dense medium’, исследуется флуктуация среднего поперечного импульса и ее зависимость от псевдобыстроты как чувствительный зонд уравнения состояния и распределения барионной плотности. Показано, что декореляция флуктуаций слабо зависит от вязкости, но может отражать различия в динамике течения барионов и антибарионов, позволяя судить о трехмерной структуре плотности энергии и барионов. Какие новые аспекты барионной материи могут быть выявлены с помощью дальнейшего анализа флуктуаций и декореляции наблюдаемых в столкновениях тяжелых ионов?

Загадка Кварк-Глюонной Плазмы: Введение в Мир Экстремальных Состояний

Столкновения релятивистских тяжелых ионов, происходящие на современных ускорителях, создают уникальное состояние материи, известное как кварк-глюонная плазма (КГП). Это не просто горячая материя, а состояние, в котором адроны, такие как протоны и нейтроны, «расплавляются», освобождая составляющие их кварки и глюоны. Температура в КГП достигает триллионов градусов Кельвина, что в десятки тысяч раз превышает температуру в центре Солнца, а плотность вещества в миллионы раз больше плотности ядерной материи. Кварк-глюонная плазма существует лишь доли секунды, но позволяет ученым изучить фундаментальные свойства сильного взаимодействия, лежащего в основе структуры адронов и, следовательно, большей части видимой Вселенной. Изучение КГП предоставляет уникальную возможность заглянуть в условия, существовавшие в первые моменты после Большого Взрыва.

Изучение динамической эволюции кварк-глюонной плазмы (КГП) представляет собой сложную вычислительную задачу, обусловленную экстремальными условиями, возникающими при столкновениях тяжелых ионов. Моделирование КГП требует учета взаимодействия огромного количества кварков и глюонов, что приводит к экспоненциальному росту вычислительных затрат. Для преодоления этих трудностей используются передовые численные методы, такие как гидродинамика и методы переноса частиц, а также высокопроизводительные вычислительные системы. Разработка точных и эффективных алгоритмов моделирования является ключевой для понимания свойств КГП, включая ее вязкость, уравнение состояния и процессы, происходящие на ранних стадиях эволюции Вселенной. $\tau_{QGP} \approx 10^{-{23}}$ секунды — типичное время жизни КГП, что подчеркивает необходимость высокоскоростных вычислений для адекватного моделирования.

Для точного описания коллективного поведения кварков и глюонов необходимы сложные теоретические модели и численные симуляции. Это обусловлено тем, что при экстремальных температурах и плотностях, характерных для кварк-глюонной плазмы, традиционные методы квантовой хромодинамики становятся неэффективными. Разработка адекватных моделей требует учета непертурбативных эффектов и сильных взаимодействий между частицами. Численные симуляции, основанные на решетчатой квантовой хромодинамике (Lattice QCD) и гидродинамических подходах, позволяют исследовать динамику плазмы и предсказывать наблюдаемые свойства, такие как анизотропия потока частиц и подавление тяжелых кварков. $\mathcal{O}(\alpha_s)$ Точность этих предсказаний напрямую зависит от вычислительных ресурсов и совершенствования алгоритмов моделирования, что представляет собой серьезную задачу для современной физики высоких энергий.

В центральных столкновениях золота при <span class="katex-eq" data-katex-display="false">\sqrt{s_{NN}} = 19.6</span> ГэВ наблюдается зависимость от быстроты величины <span class="katex-eq" data-katex-display="false">R_{pT}</span> для различных адронных комбинаций, демонстрирующая массу-зависимую декорреляцию и расщепление, вызванное конечными сохраняющимися зарядами, особенно разделение протонов и антипротонов, обусловленное плотностью барионного числа. — В центральных столкновениях золота при $\sqrt{s_{NN}} = 19.6$ ГэВ наблюдается зависимость от быстроты величины $R_{pT}$ для различных адронных комбинаций, демонстрирующая массу-зависимую декорреляцию и расщепление, вызванное конечными сохраняющимися зарядами, особенно разделение протонов и антипротонов, обусловленное плотностью барионного числа.

Гидродинамическое Моделирование: Воспроизводя Поток Кварк-Глюонной Плазмы

Гидродинамика предоставляет эффективный метод для описания эволюции кварк-глюонной плазмы (КГП), рассматривая её как жидкость, подчиняющуюся законам сохранения. Эти законы включают сохранение энергии, импульса и заряда. Математически, эволюция КГП описывается уравнениями Навье-Стокса в релятивистской форме, которые выражают связь между скоростью течения жидкости, давлением и вязкостью. Решение этих уравнений позволяет моделировать расширение и охлаждение КГП, а также предсказывать наблюдаемые экспериментальные характеристики, такие как анизотропия потока частиц. Данный подход основан на предположении, что КГП, несмотря на свою высокую температуру и плотность, проявляет коллективное поведение, характерное для жидкостей, благодаря сильным взаимодействиям между кварками и глюонами. $\partial_{\mu} T^{\mu \nu} = 0$ — фундаментальное уравнение, описывающее закон сохранения энергии-импульса в гидродинамике.

Код MUSIC реализует релятивистскую вязкую гидродинамику, что позволяет моделировать расширение и охлаждение кварк-глюонной плазмы (QGP). Этот подход основан на решении уравнений сохранения энергии, импульса и заряда, учитывающих вязкость среды. В рамках MUSIC используются численные методы, такие как метод характеристик или метод конечных разностей, для аппроксимации этих уравнений в пространстве-времени. Реализация в MUSIC позволяет варьировать параметры вязкости, такие как коэффициент сдвиговой вязкости η и объемной вязкости ζ, для изучения их влияния на динамику QGP. Полученные решения описывают эволюцию энергетической плотности, давления и скорости потока вещества, формируя основу для сравнения с экспериментальными данными, полученными в столкновениях тяжелых ионов.

Точность гидродинамического моделирования кварк-глюонной плазмы (КГП) напрямую зависит от корректного описания термодинамических свойств вещества и реалистичных начальных условий. Уравнение состояния (УСР), такое как NEoS-BQS, определяет связь между давлением, температурой и плотностью энергии КГП, что критически важно для точного расчета её эволюции. Неточности в УСР приводят к систематическим ошибкам в предсказаниях наблюдаемых величин. Наряду с этим, начальные условия, определяющие распределение энергии и плотности в момент рождения КГП, оказывают существенное влияние на результаты моделирования. Использование нереалистичных начальных условий, например, неверной геометрии или распределения энергии, также может привести к значительным отклонениям от экспериментальных данных. Таким образом, одновременное использование точного УСР и реалистичных начальных условий является необходимым условием для получения надежных результатов гидродинамического моделирования КГП.

Моделирование начинается с определения начальных условий, одним из примеров которых является модель “наклонного огненного шара” (tilted fireball). Данная модель предполагает, что столкновение тяжелых ионов не является центральным, а имеет определенный угол наклона. Это приводит к асимметричному распределению энергии в начальный момент времени, определяя начальную плотность энергии $\epsilon(x,y,z,t=0)$ в пространстве. Форма и параметры “наклонного огненного шара”, такие как степень наклона и распределение энергии, существенно влияют на дальнейшее развитие гидродинамической эволюции кварк-глюонной плазмы и, как следствие, на наблюдаемые экспериментальные данные, такие как азимутальные корреляции и спектры частиц.

За Пределами Гидродинамики: Моделируя Адронный Распад

По мере охлаждения и расширения кварк-глюонной плазмы (КГП) происходит фазовый переход в адронную материю. Этот переход, обусловленный снижением температуры и плотности энергии, приводит к образованию адронов — составных частиц, состоящих из кварков и глюонов. Процесс происходит в результате конфайнмента — явления, при котором кварки и глюоны не могут существовать в свободном состоянии, а вынуждены объединяться в адроны. Данный фазовый переход является ключевым этапом в эволюции системы, создаваемой в столкновениях тяжелых ионов, и определяет характеристики наблюдаемых адронных продуктов.

После завершения стадии гидродинамического расширения кварк-глюонной плазмы (QGP) и перехода к адронной материи, для моделирования разреженной адронной фазы используются подходы, основанные на адронном транспорте, такие как UrQMD. Эти модели описывают взаимодействие адронов посредством решения кинетических уравнений, учитывающих упругие и неупругие столкновения. UrQMD, в частности, использует каскадный алгоритм, позволяющий численно решать уравнения Больцмана для ансамбля адронов, моделируя их эволюцию во времени и пространстве. Такой подход необходим, поскольку гидродинамика становится неприменимой в разреженной адронной фазе, где средняя длина свободного пробега частиц становится сравнимой или больше характерных размеров системы.

Комбинированный подход, включающий гидродинамическое моделирование и транспортное уравнение для адронов, позволяет численно воспроизвести всю последовательность событий при столкновении тяжелых ионов. На начальных стадиях, когда плотность энергии высока, используется гидродинамика для описания эволюции кварк-глюонной плазмы. По мере охлаждения и расширения плазмы, когда плотность снижается, гидродинамическое описание становится невалидным и переходят к моделированию с использованием транспортных уравнений, таких как UrQMD, для описания взаимодействия адронов. Данный подход позволяет отследить эволюцию системы от момента начального столкновения до образования конечных частиц, что необходимо для сопоставления результатов моделирования с экспериментальными данными.

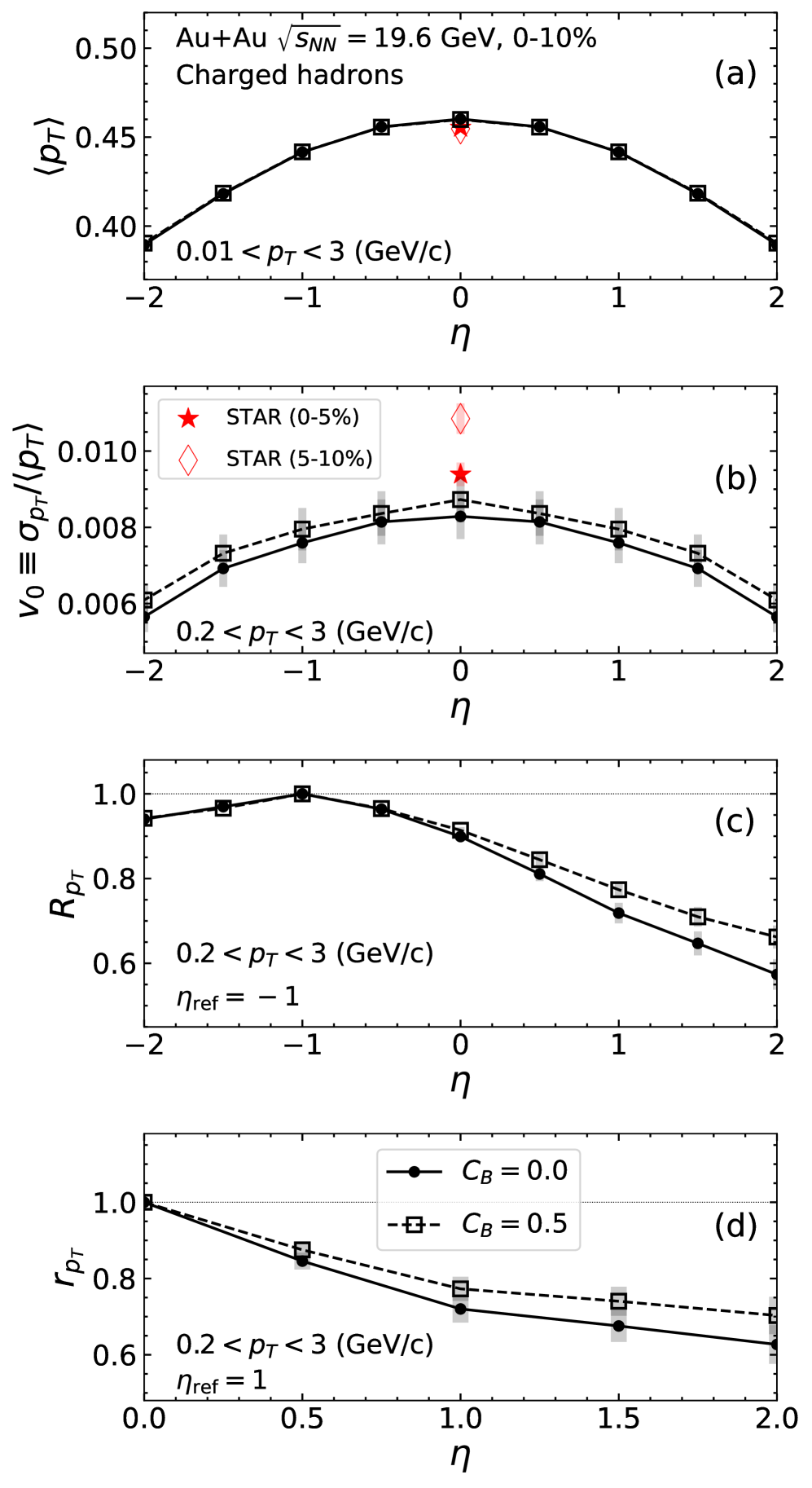
Точное моделирование диффузии барионов имеет решающее значение для получения корректного распределения чистого барионного числа в финальном состоянии симуляции столкновения тяжелых ионов. Результаты проведенных исследований показывают, что диффузия барионов оказывает незначительное влияние на конечные наблюдаемые величины, демонстрируя минимальную зависимость от параметров $R_{pT}$ и $r_{pTr}$ . Это означает, что даже при изменениях в скорости диффузии барионов, наблюдаемые характеристики частиц, формирующихся в процессе столкновения, остаются практически неизменными, что упрощает калибровку и верификацию моделей, используемых для анализа данных экспериментов.

Зависимость среднего значения <span class="katex-eq" data-katex-display="false">p_T</span> флуктуаций от псевдобыстроты показывает, что конкуренция между флуктуациями плотности энергии и плотности барионов определяет характер этой зависимости при различных начальных условиях. — Зависимость среднего значения $p_T$ флуктуаций от псевдобыстроты показывает, что конкуренция между флуктуациями плотности энергии и плотности барионов определяет характер этой зависимости при различных начальных условиях.

Флуктуации и Корреляции: Исследуя Свойства Кварк-Глюонной Плазмы

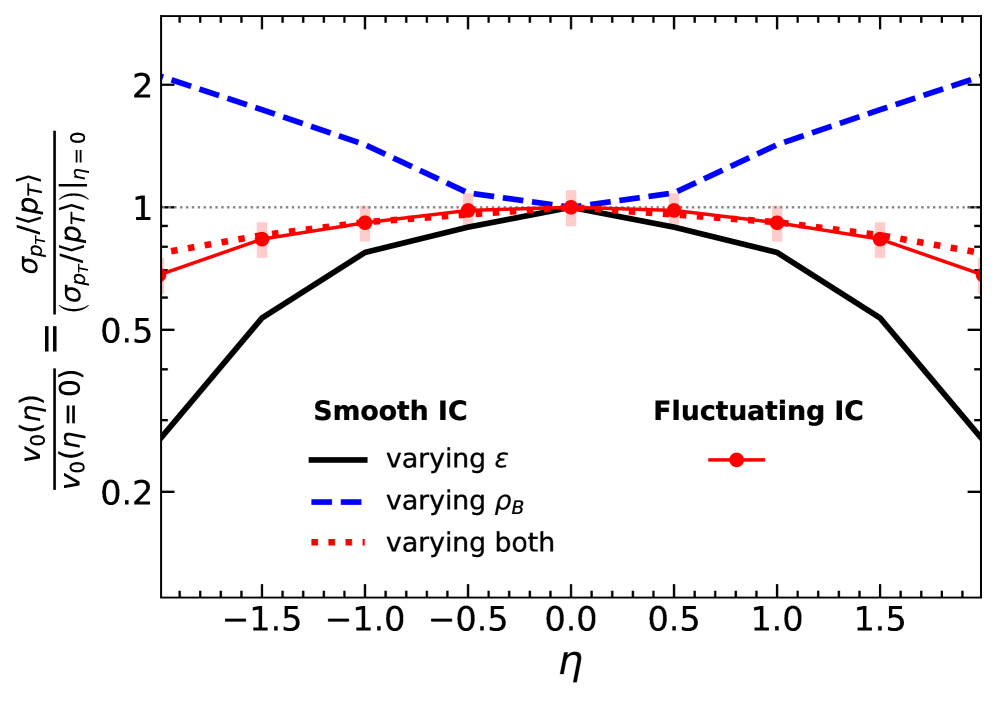
События, происходящие в ходе столкновений сверхтяжелых ионов, демонстрируют значительные флуктуации в начальных условиях и динамике развития кварк-глюонной плазмы (КГП). Эти флуктуации, проявляющиеся в распределении энергии и плотности, оказывают существенное влияние на наблюдаемые характеристики, такие как анизотропия потока и спектры частиц. Вариации в начальном профиле энергии, даже при одинаковых параметрах столкновения, приводят к различиям в формировании КГП и, как следствие, к изменениям в наблюдаемых корреляциях и потоках частиц. Исследования показывают, что учет этих флуктуаций необходим для точной интерпретации экспериментальных данных и получения более полного понимания свойств КГП, включая её вязкость и транспортные свойства. Более того, статистический анализ этих флуктуаций позволяет получить информацию о начальном состоянии системы и механизмах её эволюции.

Коллективное течение, проявляющееся как в продольном, так и в поперечном направлениях, служит ключевым индикатором отклика кварк-глюонной плазмы (КГП) на начальное распределение энергии. Изучение этого течения позволяет реконструировать плотность энергии, возникшую в момент столкновения тяжелых ионов. Наблюдаемые компоненты течения, такие как эллиптический поток, отражают асимметрию в начальном распределении энергии и, следовательно, свойства КГП. Анализ продольного течения, в свою очередь, предоставляет информацию о динамике расширения плазмы вдоль оси столкновения. Взаимосвязь между этими компонентами течения и начальными условиями является важным инструментом для понимания транспортных свойств и уравнений состояния КГП, что, в конечном счете, позволяет исследовать фазовый переход между адронной материей и кварк-глюонной плазмой.

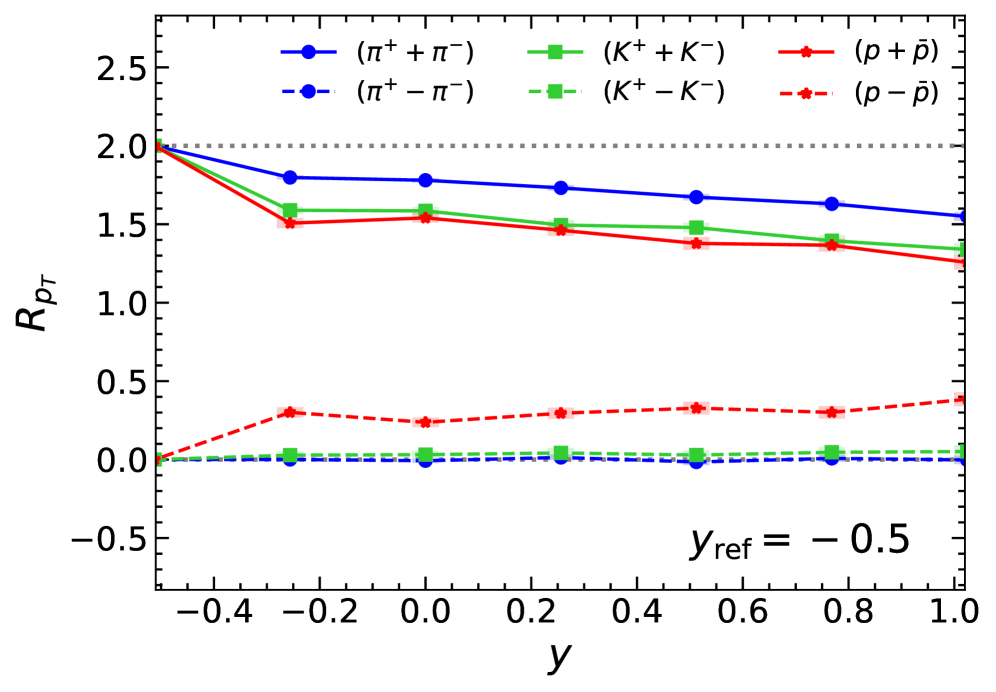
Трехбиновый коррелятор представляет собой мощный инструмент для количественной оценки декореляции по псевдобыстроте и исследования транспортных свойств кварк-глюонной плазмы. Этот метод позволяет анализировать флуктуации в распределении частиц по различным интервалам псевдобыстроты, выявляя степень их взаимосвязи. В частности, анализ корреляций позволяет оценить скорость и механизм установления теплового равновесия в QGP, а также исследовать эффекты, связанные с переносом энергии и импульса между частицами. Значительная степень декореляции указывает на быстрое рассеяние и термодинализацию, в то время как сильная корреляция может свидетельствовать о сохранении информации о начальных условиях или о наличии долгоживущих коллективных эффектов. Использование трехбинового коррелятора в экспериментах с релятивистскими тяжелыми ионами позволяет получить ценные данные о свойствах QGP, расширяя наше понимание этой экзотической фазы материи.

Вязкость, включающая как сдвиговую, так и объемную составляющие, оказывает решающее влияние на затухание коллективного течения и формирование конечного распределения импульсов в кварк-глюонной плазме. Проведенный анализ выявил значительное расщепление в радиальном течении между барионами и антибарионами, которое оценивается примерно в 30% разнице в $R_{pT}$ . Важно отметить, что основную роль в этом расщеплении играет дисперсия $p_T$ , а не ковариационный член. Кроме того, наблюдалось расщепление в $\sigma_{pT}$ , что напрямую подтверждает наличие этого различия в поведении барионов и антибарионов, указывая на более сложное взаимодействие этих частиц в условиях экстремальных температур и плотностей.

Анализ зависимости псевдобыстроты для заряженных адронов в столкновениях Au+Au при <span class="katex-eq" data-katex-display="false">\sqrt{s_{NN}} = 19.6</span> ГэВ показывает влияние диффузии барионов на величины <span class="katex-eq" data-katex-display="false">\langle p_T \rangle</span>, <span class="katex-eq" data-katex-display="false">v_0 \equiv \sigma_{pT}/\langle p_T \rangle</span>, <span class="katex-eq" data-katex-display="false">R_{pT}</span> и <span class="katex-eq" data-katex-display="false">r_{pT}</span>, что подтверждается данными STAR, полученными в средней области быстрот. — Анализ зависимости псевдобыстроты для заряженных адронов в столкновениях Au+Au при $\sqrt{s_{NN}} = 19.6$ ГэВ показывает влияние диффузии барионов на величины $\langle p_T \rangle$ , $v_0 \equiv \sigma_{pT}/\langle p_T \rangle$ , $R_{pT}$ и $r_{pT}$ , что подтверждается данными STAR, полученными в средней области быстрот.

Исследование, представленное в данной работе, демонстрирует, как флуктуации средней поперечной импульса и их зависимость от быстроты могут служить индикатором плотности барионной материи в релятивистских столкновениях тяжелых ионов. Это напоминает о бренности любого состояния системы, о неизбежности её изменения. Марк Аврелий заметил: «Всё, что мы видим, — лишь мимолетное зрелище, подобное потоку реки». Подобно тому, как река постоянно меняется, так и барионная среда эволюционирует, а анализ флуктуаций становится инструментом для понимания этой динамики. Каждый сбой в наблюдаемых данных — сигнал времени, указывающий на необходимость рефакторинга нашего понимания.

Что дальше?

Представленное исследование, подобно любому картографированию быстротекущего явления, лишь обозначило границы известного. Флуктуации средней поперечной импульса, как и любые возмущения в системе, несут информацию о её структуре, но эта информация закодирована в языке, который нам ещё предстоит полностью расшифровать. Версионирование моделей гидродинамики, неизбежно сопровождающее прогресс, — это форма памяти, попытка удержать ускользающее настоящее, зафиксировать его для последующего анализа. Однако, стрела времени всегда указывает на необходимость рефакторинга, на неизбежность пересмотра существующих представлений.

Особый интерес представляет зависимость от плотности барионов. Поиск сигналов, отличающих барион-обогащенные системы, — это не просто техническая задача, но и фундаментальный вопрос о природе материи в экстремальных условиях. Ограничения текущих моделей, неспособность адекватно описать все наблюдаемые эффекты, лишь подтверждают, что полное понимание уравнения состояния, определяющего поведение сильновзаимодействующей материи, остаётся недостижимой целью.

Будущие исследования, вероятно, будут направлены на более детальное моделирование процессов, происходящих на ранних стадиях столкновения, а также на разработку новых экспериментальных методов, позволяющих измерять флуктуации с большей точностью. Все системы стареют — вопрос лишь в том, делают ли они это достойно. И в этом смысле, поиск истины в физике высоких энергий — это непрерывный процесс, бесконечная игра с временем и материей.

Оригинал статьи: https://arxiv.org/pdf/2602.16369.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-19 19:36