Кристаллы без порядка: рождение апериодичности в смешанных бозе-эйнштейновских конденсатах

Автор: Денис Аветисян

Новое исследование показывает, что апериодические фазы могут спонтанно формироваться в бинарных бозе-эйнштейновских конденсатах под воздействием спин-зависимых оптических решеток.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал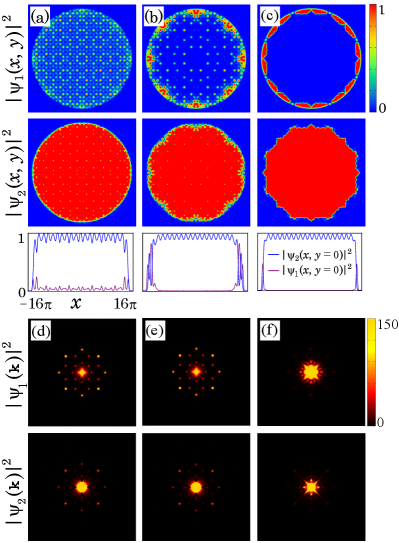

В условиях спин-зависимой периодической решетки, взаимодействие между компонентами бозе-эйнштейновского конденсата определяет формирование квазикристаллических плотностных кластеров с восьмикратной симметрией при умеренных значениях <span class="katex-eq" data-katex-display="false"> g_{12} </span>, однако при усилении этого взаимодействия происходит глобальное фазовое разделение и исчезновение квазикристаллической структуры, демонстрируя чувствительность системы к межкомпонентным взаимодействиям. — В условиях спин-зависимой периодической решетки, взаимодействие между компонентами бозе-эйнштейновского конденсата определяет формирование квазикристаллических плотностных кластеров с восьмикратной симметрией при умеренных значениях $g_{12}$ , однако при усилении этого взаимодействия происходит глобальное фазовое разделение и исчезновение квазикристаллической структуры, демонстрируя чувствительность системы к межкомпонентным взаимодействиям.

Взаимодействие между компонентами и внешние потенциалы приводят к самоорганизации апериодических квазикристаллических структур без необходимости использования апериодического удержания.

Несмотря на известные свойства периодических потенциалов в физике конденсированного состояния, природа возникновения квазикристаллического порядка в системах без апериодических решеток остается открытым вопросом. В данной работе, посвященной исследованию ‘Emergent aperiodicity in Bose-Bose mixtures induced by spin-dependent periodic potentials’, показано, что квазикристаллическая модуляция может спонтанно формироваться в бинарных конденсатах Бозе-Эйнштейна под воздействием спин-зависимых оптических решеток, обусловленная балансом между взаимодействием между компонентами и внешним потенциалом. Обнаружено, что при определенных условиях возникает устойчивая метастабильная фаза с восьмикратной симметрией, демонстрирующая переход от порядка, доминируемого решеткой, к порядку, определяемому взаимодействием. Какие новые возможности для управления квантовыми системами открывает возможность индуцирования квазикристаллического порядка без использования апериодических структур?

За пределами периодичности: рождение квазикристаллов

Традиционные материалы, такие как металлы и сплавы, характеризуются периодической структурой, где атомы располагаются в повторяющемся узоре. Эта закономерность, хотя и обеспечивает предсказуемые свойства, накладывает ограничения на возможности создания материалов с принципиально новыми характеристиками. Периодичность ограничивает диапазон возможных электронных, оптических и механических свойств, поскольку энергия электронов и распространение волн в материале определяются этой упорядоченностью. В результате, для достижения уникальных свойств, таких как высокая прочность при малом весе или необычные оптические эффекты, требуется выход за рамки этой традиционной периодичности, что и привело к открытию квазикристаллов — структур, обладающих упорядоченностью, но лишенных трансляционной симметрии.

Квазикристаллы представляют собой уникальный класс материалов, отличающийся от традиционных кристаллических структур отсутствием трансляционной симметрии — то есть, их структура не повторяется в пространстве, как у обычных кристаллов. Однако, несмотря на это, квазикристаллы демонстрируют дальний порядок, что означает наличие определённой закономерности в расположении атомов на больших расстояниях. Именно это сочетание апериодичности и дальнего порядка открывает возможности для создания материалов с необычными свойствами, такими как высокая твёрдость, низкий коэффициент трения и специфические оптические характеристики. Исследования в этой области показывают, что квазикристаллы могут найти применение в различных областях, от создания прочных и износостойких покрытий до разработки новых оптических устройств и катализаторов.

Несмотря на теоретическую элегантность и потенциальные уникальные свойства квазикристаллов, их воспроизведение и контролируемое получение в лабораторных условиях представляет собой серьезную проблему для физики конденсированного состояния. Сложность заключается в преодолении термодинамических барьеров, препятствующих формированию апериодической, но упорядоченной структуры. Экспериментальные методы, такие как быстрое охлаждение расплавов или осаждение из газовой фазы, часто приводят к образованию дефектных структур или требуют точного контроля параметров процесса. Более того, поддержание квазикристаллической фазы при комнатной температуре и атмосферном давлении остается сложной задачей, поскольку многие квазикристаллы нестабильны и стремятся к более простым, периодическим структурам. Разработка новых сплавов и методов синтеза, а также углубленное понимание механизмов формирования квазикристаллической структуры, необходимы для раскрытия всего потенциала этих необычных материалов и их практического применения.

Фазовая диаграмма сбалансированного бинарного бозе-эйнштейновского конденсата на плоскости <span class="katex-eq" data-katex-display="false">(g_{12}, U)</span>, построенная на основе параметра перекрытия <span class="katex-eq" data-katex-display="false">\mathcal{O}</span>, демонстрирует различные фазы, включая квазикристаллическую фазу (QC I) с восьмикратной симметрией в импульсном пространстве, глобально несмешиваемую фазу с <span class="katex-eq" data-katex-display="false">\mathcal{O}=0</span> и метастабильный квазикристаллический режим (QC II), характеризующийся восстановлением восьмикратной симметрии при локальном фазовом разделении. — Фазовая диаграмма сбалансированного бинарного бозе-эйнштейновского конденсата на плоскости $(g_{12}, U)$ , построенная на основе параметра перекрытия $\mathcal{O}$ , демонстрирует различные фазы, включая квазикристаллическую фазу (QC I) с восьмикратной симметрией в импульсном пространстве, глобально несмешиваемую фазу с $\mathcal{O}=0$ и метастабильный квазикристаллический режим (QC II), характеризующийся восстановлением восьмикратной симметрии при локальном фазовом разделении.

Сверххолодные газы: полигон для квазикристаллического порядка

Сверххолодные атомные системы обеспечивают беспрецедентный контроль над межчастичными взаимодействиями, что является ключевым фактором для создания квазикристаллического порядка. В отличие от традиционных материалов, где взаимодействие определяется химическим составом и кристаллической структурой, в сверххолодных газах силу и характер взаимодействия можно регулировать внешними полями, например, с помощью магнитных ловушек или лазерных полей. Это достигается за счет использования атомов с контролируемым магнитным моментом или посредством Фундаментального взаимодействия дипольных моментов. Такой контроль позволяет настраивать потенциал взаимодействия между атомами, создавая условия, необходимые для формирования непериодической, но упорядоченной структуры, характерной для квазикристаллов. Возможность точного управления этими параметрами позволяет исследовать различные фазовые переходы и изучать влияние различных взаимодействий на стабильность квазикристаллического состояния.

Дипольные квантовые газы демонстрируют перспективность в стабилизации квазикристаллических основных состояний благодаря своей анизотропной природе взаимодействия между атомами. В отличие от изотропных взаимодействий в системах с короткодействующими потенциалами, дипольные взаимодействия, обусловленные электрическими или магнитными дипольными моментами атомов, приводят к направленным силам. Эти силы способствуют формированию упорядоченных структур, не обладающих трансляционной симметрией, характерной для традиционных кристаллов, что необходимо для возникновения квазикристаллической фазы. Регулируя силу и ориентацию дипольного момента, а также плотность газа, можно настраивать параметры системы для достижения стабильных квазикристаллических состояний, которые сложно реализовать в других квантовых системах. $V(r) = \frac{C}{r^3}$ , где $C$ — константа, отражает характерный вид дипольного взаимодействия.

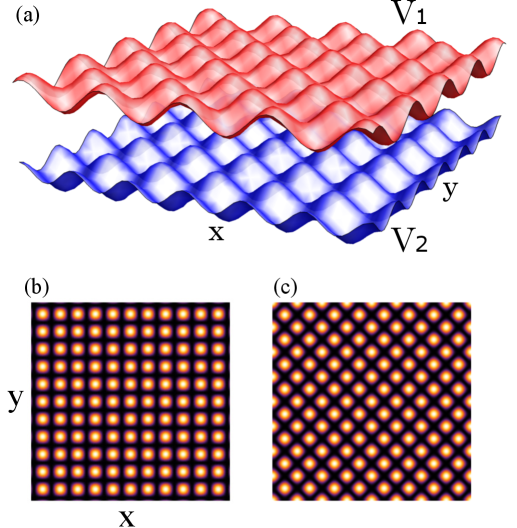
Оптические решетки используются для удержания и манипулирования ультрахолодными газами, создавая необходимые условия для формирования квазикристаллической структуры. Эти решетки формируются посредством интерференции лазерных лучей, создавая периодический потенциал, в котором атомы удерживаются. Регулируя параметры лазерного излучения — длину волны, интенсивность и поляризацию — можно точно контролировать форму и глубину потенциальных ям решетки. В этих решетках атомы, взаимодействуя друг с другом, могут самоорганизоваться в квазикристаллические структуры, характеризующиеся упорядоченностью, но не обладающие трансляционной симметрией, типичной для обычных кристаллов. Конфигурация оптической решетки является ключевым параметром для стабилизации и наблюдения различных квазикристаллических фаз.

Использование двух независимых периодических оптических решеток <span class="katex-eq" data-katex-display="false">V_1</span> и <span class="katex-eq" data-katex-display="false">V_2</span>, ориентированных под углом друг к другу, позволяет независимо управлять атомами в различных спиновых компонентах. — Использование двух независимых периодических оптических решеток $V_1$ и $V_2$ , ориентированных под углом друг к другу, позволяет независимо управлять атомами в различных спиновых компонентах.

Моделирование и подтверждение квазикристаллических фаз

Уравнения Гросса-Питайевского (УГП) представляют собой систему нелинейных дифференциальных уравнений, используемых для описания динамики бинарного бозе-эйнштейновского конденсата. В контексте исследования квазикристаллических фаз, УГП позволяют моделировать взаимодействие двух конденсированных волновых функций, описывающих различные компоненты бинарной системы. Решение УГП предоставляет информацию о пространственном распределении и временной эволюции плотности вероятности нахождения частиц в конденсате, а также о возникновении упорядоченных структур, таких как квазикристаллические решетки. Уравнения учитывают как внешние потенциалы, так и межатомные взаимодействия, определяющие энергетику и стабильность системы. $i\hbar\frac{\partial}{\partial t}\Psi(\mathbf{r},t) = \left[-\frac{\hbar^2}{2m}\nabla^2 + V(\mathbf{r}) + g|\Psi(\mathbf{r},t)|^2\right]\Psi(\mathbf{r},t)$ , где Ψ — волновая функция конденсата, $V$ — внешний потенциал, а $g$ — константа взаимодействия.

Метод Монте-Карло по траекториям (Path-Integral Monte Carlo) был использован для демонстрации устойчивости квазикристаллического порядка, несмотря на наличие квантовых флуктуаций. Данные симуляции показали, что квазикристаллическая структура сохраняется даже при учёте квантовомеханических эффектов, которые обычно приводят к разрушению порядка в системах при низких температурах. Использование функционала $\Psi = \in t D[ \phi ] e^{iS[\phi]}$ , где $S[\phi]$ — действие, позволило получить статистически значимые результаты, подтверждающие стабильность квазикристаллического состояния и его устойчивость к квантовым возмущениям.

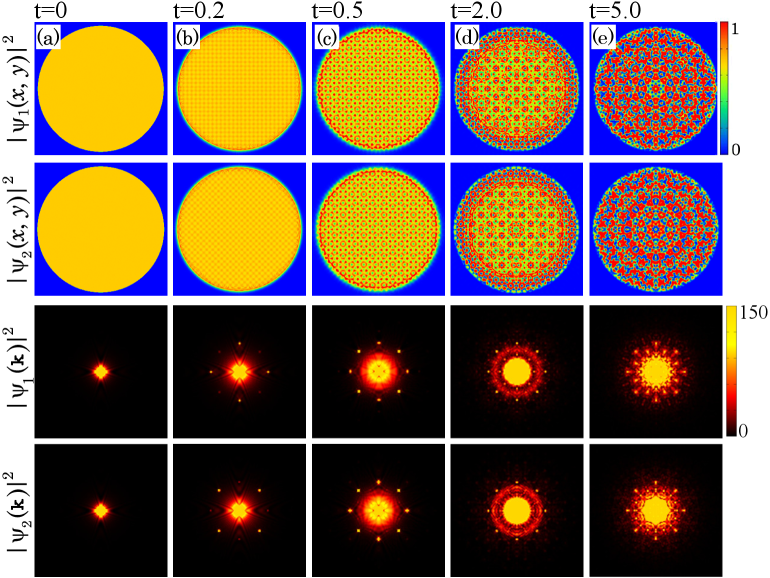
Моделирование динамики в реальном времени подтверждает теоретические предсказания относительно формирования квазикристаллической фазы. Наблюдается появление восьмикратной симметрии в структуре системы в течение временного интервала от 0.2 до 5.0 единиц времени. Данные симуляции демонстрируют эволюцию системы от начального состояния к устойчивой квазикристаллической структуре, что позволяет детально изучить механизмы самоорганизации и подтвердить предсказанные теоретические модели.

Вращающийся двукомпонентный бозе-эйнштейновский конденсат в периодической решетке с зависимостью взаимодействия от спина эволюционирует от однородного начального состояния с небольшими случайными флуктуациями при силе межкомпонентного взаимодействия <span class="katex-eq" data-katex-display="false">g_{12} = 16.5</span>. — Вращающийся двукомпонентный бозе-эйнштейновский конденсат в периодической решетке с зависимостью взаимодействия от спина эволюционирует от однородного начального состояния с небольшими случайными флуктуациями при силе межкомпонентного взаимодействия $g_{12} = 16.5$ .

Раскрытие эмерджентных свойств и фазовых переходов

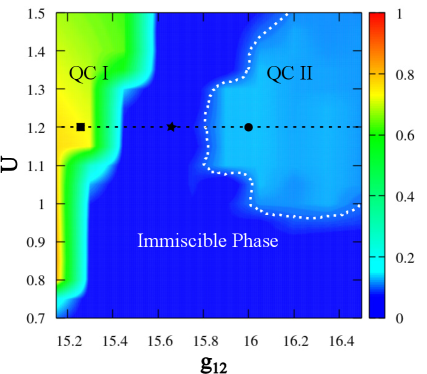
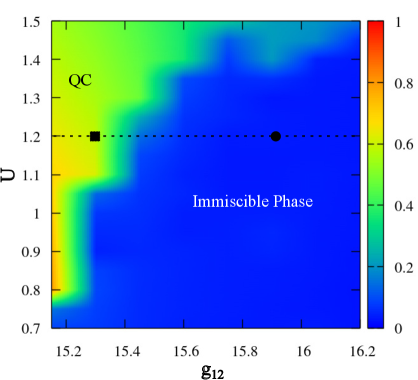
Взаимодействие между компонентами в бинарном бозе-эйнштейновском конденсате играет ключевую роль в формировании фазового поведения и симметрии системы. Исследования показывают, что сила и характер этого взаимодействия напрямую определяют, как компоненты самоорганизуются, формируя различные фазы — от раздельных до смешанных. В частности, изменение параметров взаимодействия между компонентами приводит к возникновению новых структур, таких как кластеры с восьмикратной вращательной симметрией. Регулируя $g_{12}$ — силу взаимодействия между компонентами, ученые могут контролировать фазовые переходы и создавать системы с заданными свойствами, что открывает перспективы для создания новых материалов и устройств, использующих квантовые явления.

Исследования показывают, что переход от несмешивающейся к смешивающейся фазе в бинарном бозе-эйнштейновском конденсате тесно связан с возникновением восьмикратной вращательной симметрии в структурах плотности. Этот феномен наблюдается при определённых параметрах взаимодействия между компонентами конденсата, когда система спонтанно организуется в кластеры, демонстрирующие уникальную симметрию. Формирование таких структур с восьмикратной симметрией указывает на появление новых, эмерджентных свойств, отличающихся от поведения отдельных компонентов. $g_{12}$ — параметр, определяющий силу межкомпонентного взаимодействия, играет ключевую роль в управлении этим переходом и, как следствие, в формировании упорядоченных структур с высокой степенью симметрии, что открывает перспективы для создания новых материалов с заданными оптическими и квантовыми свойствами.

Исследования показали, что фазовое поведение бинарных бозе-эйнштейновских конденсатов может быть эффективно контролируемо посредством настройки двумерных периодических потенциалов, зависящих от компонента, и спин-зависимых периодических потенциалов. В частности, ключевые результаты, демонстрирующие значительное изменение фазового поведения системы, наблюдались при силе межкомпонентного взаимодействия, равной $g_{12} = 16.5$ . Такое точное управление потенциалами позволяет формировать и контролировать структуру конденсата, открывая возможности для создания новых состояний материи с заданными свойствами и потенциальными применениями в квантовых технологиях. Установлено, что варьирование параметров потенциалов напрямую влияет на стабильность и форму плотностных кластеров, что является важным фактором для управления квантовыми свойствами системы.

Диаграмма фаз несбалансированного бинарного бозе-эйнштейновского конденсата на плоскости (<span class="katex-eq" data-katex-display="false">g_{12}, U</span>) показывает сосуществование квазикристаллического порядка (как показано на рис. 4(b)) и полную несмешиваемость (рис. 4(c)), определяемые параметром перекрытия <span class="katex-eq" data-katex-display="false">\mathcal{O}</span>. — Диаграмма фаз несбалансированного бинарного бозе-эйнштейновского конденсата на плоскости ( $g_{12}, U$ ) показывает сосуществование квазикристаллического порядка (как показано на рис. 4(b)) и полную несмешиваемость (рис. 4(c)), определяемые параметром перекрытия $\mathcal{O}$ .

К созданию материалов с заданными квазикристаллическими свойствами

Параметр перекрытия, используемый совместно с фазовой диаграммой, представляет собой количественный инструмент для точной характеристики различных фаз квазикристаллического вещества. Этот параметр, по сути, измеряет степень упорядоченности и взаимосвязанности атомов в структуре материала. Значение, стремящееся к единице, указывает на высокую степень порядка и сильное взаимодействие между фазами, в то время как значение, равное нулю, свидетельствует о полной сепарации фаз — то есть, о полном отсутствии смешивания и формировании отдельных, четко разграниченных областей с различными свойствами. Точное определение параметра перекрытия позволяет исследователям не только идентифицировать различные фазовые состояния, но и предсказывать и контролировать свойства квазикристаллов, открывая путь к созданию материалов с заданными характеристиками. $\text{Overlap Parameter} = 0 \implies \text{Complete Phase Separation}$

Оптические решетки с восьмикратной вращательной симметрией представляют собой перспективный инструмент для практической реализации и контроля экзотических квантовых состояний, таких как квазикристаллические фазы. В этих системах, атомы удерживаются в периодической потенциальной яме, создаваемой интерферирующими лазерными лучами, образующими узор с восьмикратной симметрией. Тщательно контролируя параметры лазеров — интенсивность, частоту и поляризацию — ученые могут настраивать потенциал и, таким образом, управлять взаимодействием между атомами. Эта возможность точного контроля позволяет исследовать фазовые переходы между различными квантовыми состояниями, в том числе и в областях, недоступных для традиционных кристаллических систем. Благодаря высокой степени контроля и возможности масштабирования, подобные оптические решетки открывают путь к созданию и изучению новых материалов с уникальными свойствами, потенциально революционизирующих области от квантовых вычислений до материаловедения.

Состояние сверхтекучего квазикристалла представляет собой принципиально новую квантовую фазу материи, открывающую захватывающие перспективы в материаловедении и за его пределами. Исследования показывают, что данное состояние характеризуется одновременным проявлением упорядоченной, но непериодической структуры, свойственной квазикристаллам, и способности к диссипации энергии без вязкости, присущей сверхтекучим жидкостям. Эта уникальная комбинация свойств позволяет предположить возможность создания материалов с беспрецедентной проводимостью, механической прочностью и термостабильностью. $\text{Потенциальные применения охватывают широкий спектр областей, от разработки высокоэффективных сенсоров и квантовых компьютеров до создания новых поколений сверхпроводящих материалов и устройств хранения энергии.}$ Изучение этого экзотического состояния материи требует междисциплинарного подхода, объединяющего принципы квантовой механики, физики конденсированного состояния и материаловедения, и обещает революционные открытия в будущем.

Данное исследование демонстрирует, как взаимодействие компонентов в бинарных бозе-эйнштейновских конденсатах, находящихся под воздействием спин-зависимых периодических потенциалов, может спонтанно приводить к формированию апериодических квазикристаллических фаз. Это напоминает о фундаментальной человеческой склонности искать порядок даже там, где его изначально нет. Как заметила Мэри Уолстонкрафт: «Невозможно надеяться на разумность там, где преобладает страсть». В контексте этой работы, «страсть» можно рассматривать как стремление системы к минимизации энергии, а «разумность» — как упорядоченную структуру. Попытка предсказать поведение системы, основанная на этой модели, всегда будет подвержена систематическим ошибкам, ведь даже кажущаяся предсказуемость — это лишь коллективная иллюзия, порожденная надеждами и страхами, выраженная в графиках.

Что дальше?

Представленная работа, демонстрируя спонтанное возникновение апериодических фаз в смесях бозе-бозе, словно бы заново открывает старую истину: порядок — это лишь локальное упрощение, маскирующее фундаментальную неопределённость. Не стоит, однако, видеть в этом триумф математической элегантности. Вместо этого, стоит задаться вопросом, насколько эти искусственно созданные квазикристаллические структуры отражают реальные физические системы, или же являются лишь проекцией нашего стремления к упорядочиванию хаоса. Все модели решают не экономические, а экзистенциальные проблемы — как справиться с неопределённостью.

Очевидным направлением дальнейших исследований представляется изучение влияния флуктуаций и несовершенств потенциалов на стабильность этих апериодических фаз. Насколько чувствительны они к внешним возмущениям? Способны ли они самоорганизовываться в более сложные, устойчивые структуры? Важно также исследовать возможность применения этих систем для моделирования других апериодических систем, например, спиновых стёкол или биологических структур, где хаос и порядок переплетены неразрывно.

В конечном счёте, ценность подобных исследований заключается не в создании идеальных квазикристаллов, а в углублении понимания фундаментальных принципов самоорганизации и сложности. Человек не рациональный агент, а биологическая гипотеза с систематическими ошибками, и, возможно, именно в признании этой ошибки лежит путь к истинному пониманию мира.

Оригинал статьи: https://arxiv.org/pdf/2602.13129.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-17 03:31