Автор: Денис Аветисян
Новое исследование показывает ограничения метода стохастических траекторий при моделировании сложных квантовых систем, таких как модель Тависа-Каммингса.
Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.
Бесплатный телеграм-канал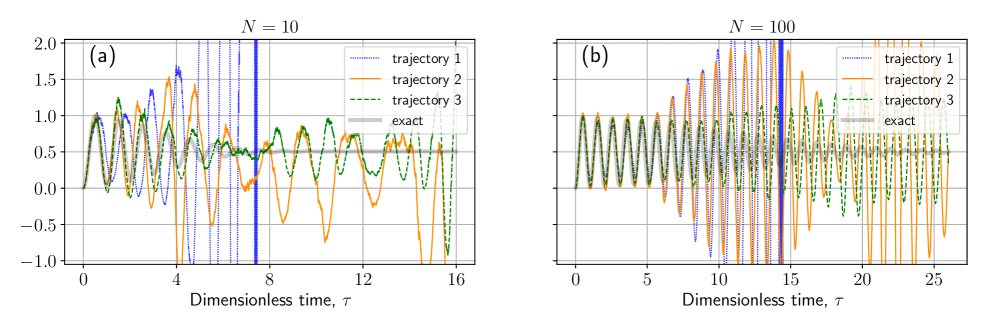
Критический анализ применимости метода стохастических траекторий к модели Тависа-Каммингса и стратегии смягчения расходимости траекторий.
Несмотря на перспективность стохастических методов для моделирования квантовой динамики многочастичных систем, их применимость часто ограничена возникновением расходимостей. В данной работе, ‘Modelling many-body quantum dynamics with stochastic trajectories: a critical test on the Tavis-Cummings model’, критически исследуется эффективность нового подхода, основанного на стохастических траекториях, для анализа модели Тависа-Каммингса. Полученные результаты демонстрируют, что расходимость траекторий ограничивает время достоверного моделирования, несмотря на попытки регуляризации с помощью различных преобразований. Возможно ли преодолеть эти ограничения и расширить область применимости стохастических методов для изучения сложных квантовых систем с выраженными когерентными эффектами?
Открытые Квантовые Системы: Вызовы Моделирования
Описание динамики открытых квантовых систем, взаимодействующих с окружающей средой, представляет собой сложную задачу, требующую приближений из-за высокой размерности. Точное решение уравнений движения часто вычислительно непосильно, особенно для больших систем. Традиционные подходы быстро становятся ресурсоемкими. Ключевая сложность – адекватный учет шума без внесения артефактов. Для решения этой проблемы активно разрабатываются методы, основанные на моделировании Монте-Карло и других стохастических подходах. Эффективное моделирование требует не только вычислительной мощности, но и глубокого понимания физических процессов. Данные – это компромисс между шумом и моделью.

Стохастические Траектории: Вычислительный Путь
Метод стохастических траекторий использует стохастические дифференциальные уравнения для моделирования квантовой динамики, заменяя сложное квантовомеханическое описание набором классических траекторий. В основе метода – отображение квантовой системы на ансамбль классических траекторий с добавлением случайного шума, отражающего квантовые флуктуации. Точность моделирования зависит от корректного выбора параметров шума и количества траекторий. Ключевым аспектом является использование Ito-исчисления для строгой математической обработки этих процессов, обеспечивающего высокую точность при моделировании.

Укрощение Траекторий: Смещение и Регуляризация
Неконтролируемые стохастические симуляции подвержены феномену неуправляемых траекторий, приводящему к неточности результатов и нестабильности системы. Трансформация смещения позволяет модифицировать детерминированную часть стохастического дифференциального уравнения, контролируя поведение неуправляемых траекторий без изменения математического ожидания. Включение диссипации в модель посредством квантового мастер-уравнения выступает в роли регуляризующего механизма, обеспечивающего стабильность и физическую релевантность симуляций. Установлено, что для обеспечения стабильных симуляций с начальными возбуждениями требуется параметр затухания $\gamma/f = 2.6$.

Упрощения и Пределы: Область Эффективности
Метод стохастических траекторий в сочетании с техниками, снижающими размерность, позволяет эффективно моделировать сложные системы, в частности, те, которые описываются моделью Тависа-Каммингса. Метод особенно эффективен при исследовании полуклассического предела, где квантовые эффекты менее выражены. Исследование статистических взаимосвязей посредством корреляционной функции и характеристика шумового члена необходимы для валидации точности модели. В конечном итоге, успешное моделирование требует не только вычислительной мощности, но и критического подхода к интерпретации результатов – если картина получается слишком красивой, вероятно, стоит перепроверить исходные данные.

Исследование, представленное в данной работе, подчеркивает сложность моделирования многочастичной квантовой динамики. Авторы столкнулись с проблемой расхождения траекторий, ограничивающей возможности долгосрочного моделирования системы Тависа-Каммингса. Подобные трудности неизбежны при попытке приблизительного описания квантовых систем, где точность всегда ограничена вычислительными ресурсами. Как однажды заметил Эрвин Шрёдингер: «Всякая теория, которая не может быть проверена экспериментально, — это всего лишь красивый рассказ». Данное исследование, применяя методы диссипации и преобразования калибровочного поля, стремится к более надежным результатам, осознавая, что даже самые изящные модели требуют постоянной проверки на соответствие реальности. Попытки обуздать расхождение траекторий – это не просто техническая задача, а отражение фундаментального стремления к точности в науке.
Что дальше?
Представленные результаты, как и следовало ожидать, не предлагают окончательных ответов, а лишь уточняют границы применимости метода стохастических траекторий к модели Тависа-Каммингса. Расхождение траекторий, ограничивающее долгосрочное моделирование, – это не столько фундаментальное препятствие, сколько напоминание о том, что любая параметризация реальности неизбежно вносит искажения. Данные – не цель, а зеркало человеческих ошибок. Попытки смягчить расхождение посредством введения диссипации или преобразований калибровочного поля, безусловно, заслуживают дальнейшего изучения, однако следует помнить: подавление симптомов не всегда избавляет от болезни.
Более продуктивным представляется поиск альтернативных подходов к выборке фазового пространства. Текущие методы, ориентированные на простоту реализации, часто упускают из виду сложные корреляции, определяющие квантовую динамику. Всё, что нельзя измерить, всё равно влияет – просто это труднее моделировать. Настало время сместить акцент с грубой силы численных вычислений на разработку более элегантных алгоритмов, способных улавливать тонкости квантового поведения.
В конечном счёте, задача моделирования многочастичных квантовых систем – это не поиск идеальной модели, а непрерывный процесс проверки, опровержения и уточнения. Рациональность – это не холодность, а привычка подвергать сомнению даже собственные выводы. Следующие шаги должны быть направлены не на устранение всех неточностей, а на их систематическое изучение и количественную оценку.
Оригинал статьи: https://arxiv.org/pdf/2511.08815.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Решение головоломки с паролем Absolum в Yeldrim.
- Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip
- Все коды в Poppy Playtime Глава 4
- Объяснение каждого Таргариена в «Рыцаре семи королевств»
- Акции VTBR. Банк ВТБ: прогноз акций.
- Лучшие шаблоны дивизий в Hearts Of Iron 4
- Акции UGLD. Южуралзолото ГК: прогноз акций.
- Где находится точка эвакуации «Туннель контрабандистов» на локации «Интерчейндж» в Escape from Tarkov?
- Roblox: Коды для тренировки с копьем.
- Цивилизация 6: Полное руководство
2025-11-13 14:43