Квантовая геометрия материалов: новый взгляд на сцепление и локализацию электронов

Автор: Денис Аветисян

---

Исследование устанавливает связь между квантовой геометрией, запутанностью и линейным откликом в диэлектриках, открывая новые возможности для характеристики электронных свойств материалов.

В работе продемонстрировано, как метрика Бюреса и квантовая информация Фишера могут использоваться для изучения локализации электронов и ковалентной связи в диэлектриках и металлах.

Квантово-геометрические свойства материалов, определяющие многие фундаментальные характеристики, долгое время оставались недоступными для прямого экспериментального изучения. В работе ‘Fundamental Tests of Quantum Geometric Bounds in Ionic and Covalent Insulators using Inelastic X-Ray Scattering’ продемонстрировано, что непругое рассеяние рентгеновских лучей (IXS) является прямым и количественным методом исследования квантовой геометрии и квантовой информации в твердых телах. Измерение отклика на возмущения в двух прототипных изоляторах — алмазе с ковалентной связью и LiF с ионной — позволило экспериментально определить квантовую информационную метрику Буреса и длину локализации электронов. Какие новые возможности открывает IXS для изучения связи между квантовой информацией, химической связью и фундаментальными свойствами материалов?

---

Геометрия Квантового Состояния: За Гранью Волновой Функции

Традиционные квантовые описания, основанные на анализе волновых функций, часто оказываются недостаточными при изучении сложных многочастичных систем. В частности, при рассмотрении систем с сильными взаимодействиями между частицами, или при возникновении коллективных, эмерджентных свойств, стандартные подходы теряют свою эффективность. Это связано с тем, что волновые функции могут становиться чрезвычайно сложными и трудно интерпретируемыми, а простое описание на основе отдельных частиц перестает отражать реальную физику системы. Вместо этого, необходимо учитывать геометрию квантового пространства состояний, которая определяет, как сильно различаются соседние состояния и как частицы взаимодействуют друг с другом, что открывает путь к более полному и адекватному пониманию поведения материала и предсказанию его свойств. Игнорирование этой геометрической структуры может привести к неверным выводам и невозможности объяснить наблюдаемые явления.

Квантенный геометрический тензор представляет собой мощную обобщающую концепцию, позволяющую полностью описать геометрию квантового состояния. Он объединяет в себе два ключевых элемента: кривизну Берри и кванметрику. Кривизна Берри, \Omega_{ij}, описывает фазовые эффекты, возникающие при адиабатическом изменении параметров системы, в то время как кванметрика, g_{ij}, определяет расстояние между бесконечно близкими квантовыми состояниями. Вместе они формируют полный геометрический ландшафт, позволяющий рассматривать квантовые системы не просто как волны, но и как объекты, существующие в многомерном геометрическом пространстве, где свойства материала определяются этой геометрией, а не только его волновой функцией. Такой подход открывает новые возможности для понимания и контроля над сложными квантовыми системами и материалами.

Понимание геометрического ландшафта квантовых состояний имеет решающее значение для предсказания и контроля поведения материалов, выходя за рамки простого анализа волновых функций. Традиционные методы часто оказываются недостаточными при описании сложных многочастичных систем, где взаимодействие между частицами создает нетривиальную геометрию. Исследование Quantum Geometric Tensor, включающего как кривизну Берри, так и кванметрику, позволяет получить полное представление об этой геометрии и ее влиянии на динамические свойства материала. Вместо того, чтобы рассматривать электроны как волны, движущиеся в статическом потенциале, этот подход рассматривает их как геометрические объекты, перемещающиеся по искривленному пространству, что позволяет предсказывать и управлять такими явлениями, как проводимость, сверхпроводимость и топологические фазы материи с большей точностью и эффективностью. Таким образом, переход к геометрическому описанию открывает новые возможности для разработки материалов с заданными свойствами и создания инновационных технологий.

Методы Характеристики Квантового Состояния: Зондирование Геометрии

Неупругое рассеяние рентгеновских лучей (IXS) предоставляет прямой метод измерения квантового веса, который тесно связан с динамическим фактором структуры. IXS позволяет определить величину квантового веса путем анализа сдвига энергии рассеянных фотонов, что напрямую связано с энергией возбуждений в исследуемой системе. Данный метод особенно эффективен для определения динамического фактора структуры S(q, \omega), представляющего собой вероятность перехода системы из начального состояния в конечное с изменением импульса q и энергии ω. Точность измерения квантового веса, полученного посредством IXS, критически важна для последующего анализа и характеризации квантовых состояний, поскольку он служит ключевым параметром для определения степени различимости между ними.

Квантовый вес является обобщением понятия квантовой информации Фишера и используется для оценки чувствительности к малым возмущениям в квантовых состояниях. Его точное определение требует знания статического фактора рассеяния, который описывает корреляции между частицами в системе и определяет распределение импульсов. S(q) — статический фактор рассеяния, непосредственно влияет на точность вычисления квантового веса, поскольку он определяет вклад различных волновых векторов в общую чувствительность к возмущениям. Таким образом, для получения достоверных результатов при использовании квантового веса, необходимо точное экспериментальное или теоретическое определение статического фактора рассеяния.

Количественная оценка различимости квантовых состояний осуществляется посредством буресова расстояния, основой для которого является верность (fidelity). Буресово расстояние позволяет проводить точную геометрическую характеризацию квантовых состояний, поскольку оно напрямую связано с продольной компонентой квантической метрики. В частности, буресова метрика является аналогом римановой метрики в пространстве квантовых состояний, а ее связь с продольной компонентой квантической метрики обеспечивает меру изменения состояния при бесконечно малых возмущениях. Это позволяет использовать геометрические методы для анализа и сравнения различных квантовых состояний, а также для оптимизации квантовых протоколов. Формально, буресово расстояние между двумя состояниями ρ и σ определяется как D_B(\rho, \sigma) = \sqrt{1 - F(\rho, \sigma)}, где F(\rho, \sigma) — верность, а связь с квантической метрикой описывается через g_{ij} = \text{Tr}(\rho \frac{\partial \rho}{\partial \theta_i} \frac{\partial \rho}{\partial \theta_j}).

Материальные Свойства и Проводимость: Связь с Геометрией

Квантрическая метрика (\mathcal{Q}[latex]) напрямую связана с продольной проводимостью, описывая реакцию носителей заряда на воздействие электрических полей. Данная метрика количественно определяет чувствительность электронного волнового пакета к изменениям в геометрии кристаллической решетки или внешних электрических полях. В частности, компоненты квантрической метрики определяют, насколько сильно изменяется скорость носителей заряда при приложении электрического поля, что непосредственно влияет на величину продольной проводимости [latex]\sigma_x. Более высокие значения квантрической метрики указывают на более сильную зависимость скорости носителей заряда от внешних воздействий и, следовательно, на повышенную проводимость вдоль соответствующего направления.

Рассеивающие компоненты электропроводности напрямую связаны с флуктуациями, описываемыми квантовой метрикой. Данная метрика количественно определяет чувствительность системы к возмущениям и, следовательно, определяет вклад в потери энергии при протекании электрического тока. Увеличение флуктуаций, зафиксированных квантовой метрикой \mathcal{Q}, коррелирует с ростом диссипативных эффектов, что проявляется в уменьшении проводимости и увеличении выделяемого тепла. Таким образом, квантовая метрика выступает ключевым параметром, характеризующим энергетические потери в материалах, и позволяет оценить эффективность переноса заряда в различных системах.

Взаимосвязь между скрученными граничными условиями и квантовой метрикой демонстрирует возможность управления материальными свойствами посредством геометрического контроля. Полученные границы для квантовой информации Фишера, основанные на энтропии запутанности и статической функции структуры, количественно характеризуют эту взаимосвязь. В частности, установлено, что изменение скручивания границ влияет на величину QFI, что указывает на возможность настройки проводимости и других свойств материала путем геометрической деформации. Степень влияния скручивания на QFI напрямую связана с уровнем запутанности в системе и характеристиками статического упорядочения, что позволяет прогнозировать и контролировать поведение материала на основе этих параметров.

Топологические Аспекты: Запутанность и Модельные Системы

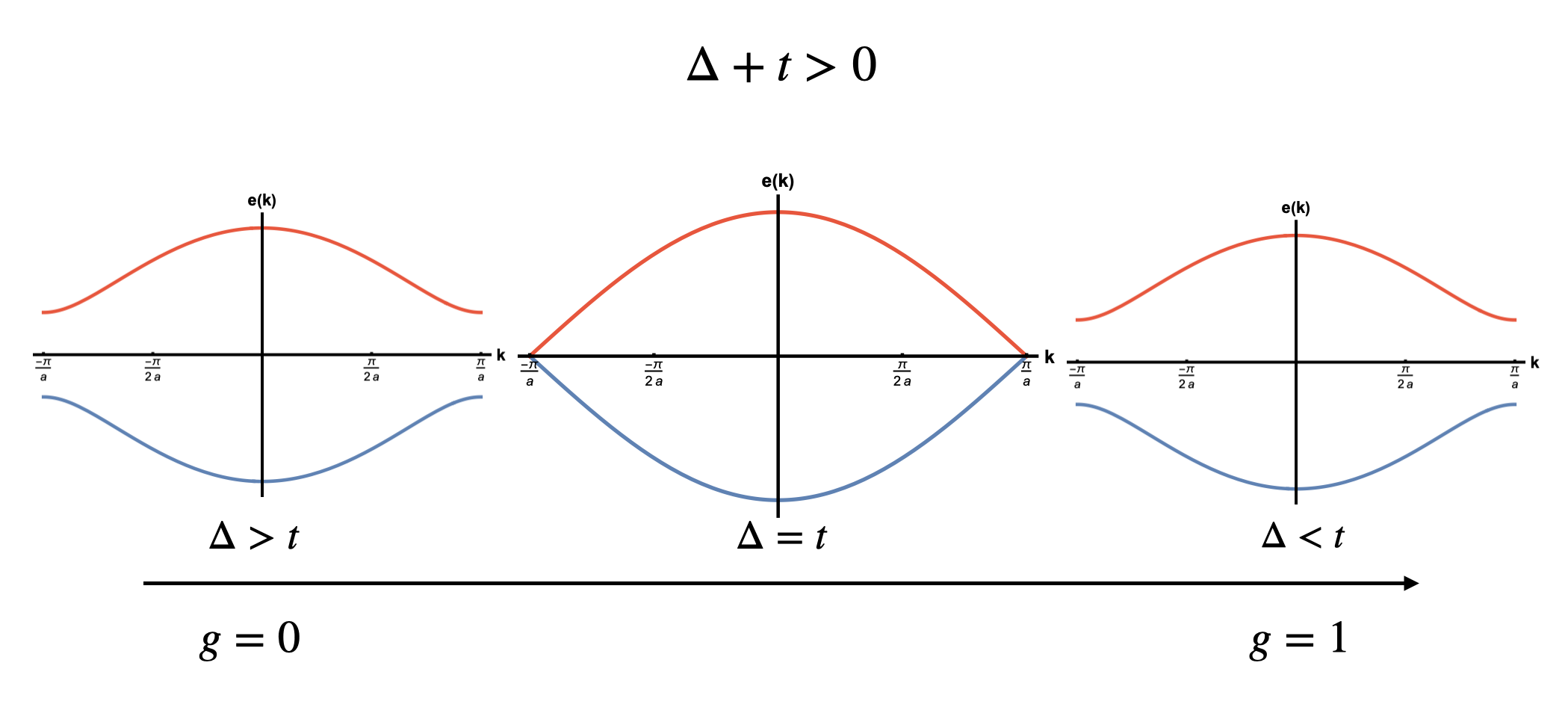
Модели, такие как модель Су-Шриффера-Хигера и более общая модель плотной связи, не просто описывают электронную структуру материалов, но и фундаментально основаны на явлении квантовой запутанности. Эти модели служат важнейшими полигонами для исследования геометрических аспектов квантовой механики, позволяя изучать, как топологические свойства влияют на поведение электронов. В частности, запутанность в этих моделях проявляется как корреляция между электронами на разных участках кристаллической решетки, определяющая проводимость и другие ключевые характеристики материала. Использование этих теоретических конструкций позволяет исследователям прогнозировать и контролировать квантовые свойства новых материалов, открывая перспективы для создания устройств с улучшенными характеристиками и принципиально новыми функциональными возможностями.

Квантовый вес представляет собой расширение понимания запутанности в моделях, таких как модель Су-Шриффера-Хигера, предоставляя более глубокую меру квантовых корреляций между частицами. Этот показатель позволяет выйти за рамки традиционных мер запутанности, отражая более сложные взаимосвязи в электронных структурах материалов. Недавние экспериментальные исследования, проведенные с использованием неэластичного рентгеновского рассеяния (IXS), подтвердили соответствие измеренных значений квантового веса теоретическим предсказаниям для ковалентной и ионной связи. В частности, полученные результаты демонстрируют, что величина квантового веса тесно связана с характером химической связи, позволяя, таким образом, оценивать вклад различных типов связи в общие электронные свойства материала и потенциально управлять ими для создания материалов с заданными характеристиками.

Сочетание теоретических моделей, таких как модель Су-Шриффера-Хигера и модель плотной связи, с передовыми экспериментальными методами открывает возможности для целенаправленного конструирования материалов с заданными топологическими свойствами и функциональностью. Исследования показали, что существуют четкие границы для квантовой информации Фишера, которые тесно связаны с характером ковалентной связи как в упрощенных моделях, так и в реальных материалах, например, в алмазе. Это позволяет не только глубже понимать фундаментальные квантовые корреляции, но и разрабатывать новые стратегии для создания материалов с улучшенными или совершенно новыми свойствами, используя топологию как инструмент для управления материей на квантовом уровне.

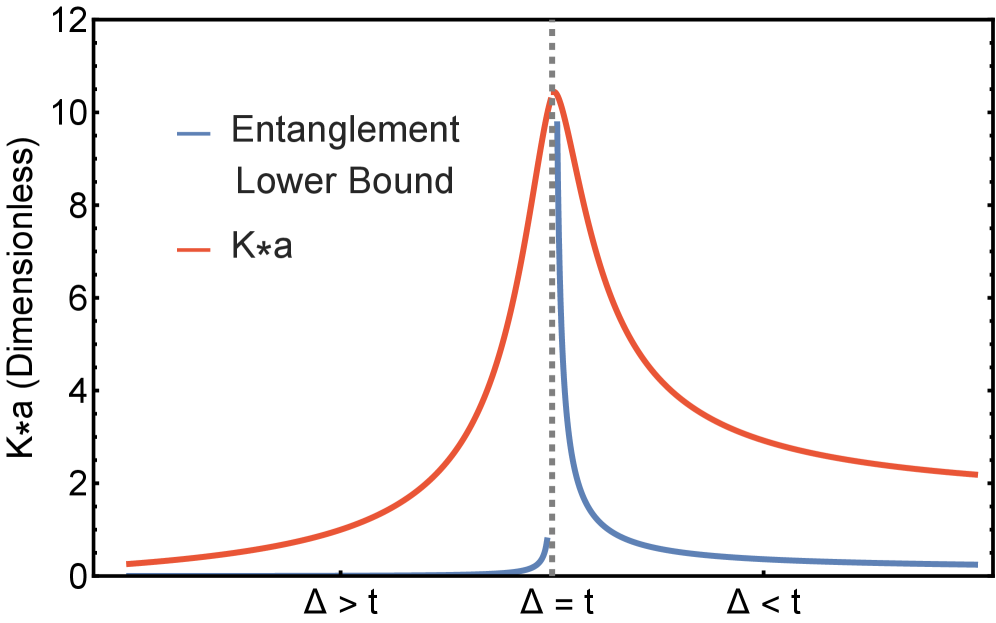
Исследование связывает квантовую геометрию с линейными откликами в материалах, что неизбежно напоминает о вечной борьбе между теорией и практикой. Авторы демонстрируют, как метрика Бюреса и квантовая информация Фишера могут характеризовать локализацию электронов. И как же часто бывает, элегантная математическая модель сталкивается с суровой реальностью несовершенства материалов. Как говорил Жан-Поль Сартр: «Существование предшествует сущности». В данном случае, существование несовершенств в материалах предшествует любой попытке их идеального описания. Иначе говоря, неважно, насколько красива теория, всегда найдется дефект, который её опровергнет. Вполне вероятно, что следующая «революционная» методика анализа тоже станет лишь источником новых ошибок.

Что Дальше?

Представленная работа, безусловно, выстраивает элегантный мостик между абстракциями квантовой геометрии и вполне себе приземлёнными характеристиками материалов. Однако, как показывает опыт, любое «красивое» теоретическое построение рано или поздно столкнётся с суровой реальностью производственного процесса. Рассчеты, основанные на идеализированных условиях, неизбежно потребуют корректировки, когда речь зайдет о реальных образцах с дефектами, примесями и прочими несовершенствами. Иначе говоря, “геометрия” быстро превратится в головную боль для тех, кто попытается её применить.

Более того, не стоит забывать, что метрика Бюреса и квантовая информация Фишера - это лишь инструменты. Их полезность напрямую зависит от возможности их точного измерения в сложных системах. Учитывая, что эксперименты с рассеянием рентгеновских лучей - процесс недешёвый и требующий ювелирной точности, вопрос о масштабируемости данного подхода остаётся открытым. Пока же, скорее всего, мы увидим всё больше “красивых картинок” и всё меньше практических приложений.

В конечном счете, исследование квантовой геометрии - это увлекательная игра с фундаментальными концепциями. Но как и в любой игре, всегда есть риск проиграть. И, судя по опыту, производство всегда находит способ превратить теорию в техдолг.

---

Оригинал статьи: https://arxiv.org/pdf/2601.19054.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

• Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip

• Решение головоломки с паролем Absolum в Yeldrim.

• Все рецепты культистского круга в Escape from Tarkov

• Лучшие шаблоны дивизий в Hearts Of Iron 4

• Лучшие транспортные средства в Far Cry 6

• Необходимо: Как выращивать урожай

• All Valley Pass Aurylene Locations In Endfield

• Палия: где найти сердечную лилию

• Как получить кинжалы Небесного ключа в Dragon’s Dogma 2

• В ролях: приглашенные звезды и актеры 22-го сезона 3-й серии «Морской полиции» (фотографии) – Донна Миллс в беде с Хэлом

2026-01-29 01:29