Автор: Денис Аветисян
В статье представлена квантовая гиперравномерность как мощный инструмент для анализа квантовых состояний и фазовых переходов, позволяющий выявлять различные классы систем по степени подавления квантовых флуктуаций.
Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.
Бесплатный телеграм-канал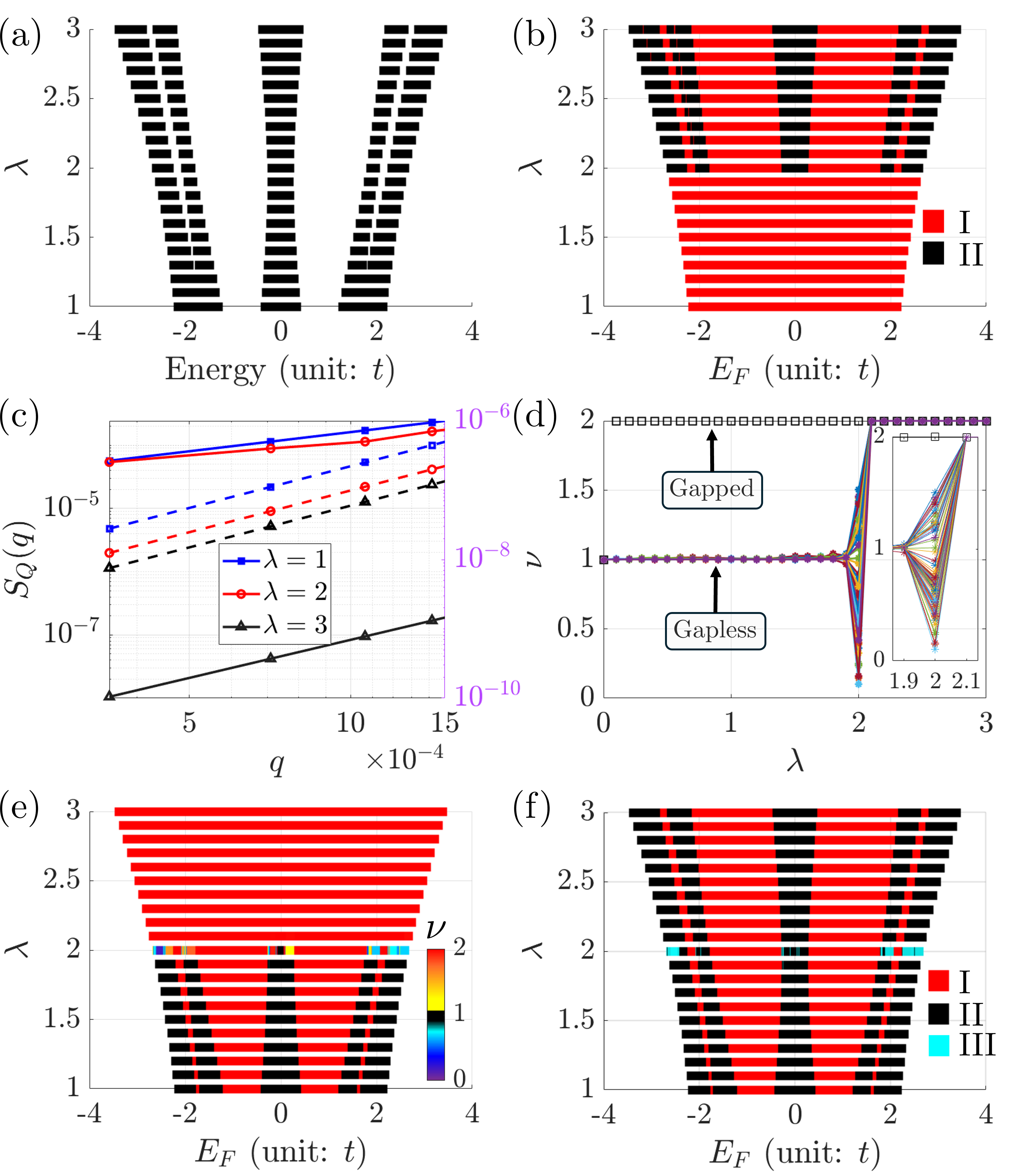
Исследование демонстрирует применимость концепции квантовой гиперравномерности к квазипериодическим системам, таким как модель Обри-Андре, и ее связь с критическими состояниями и безынтервальными фазами.
Несмотря на широкое применение анализа флуктуаций в изучении квантовых систем, выявление универсальных характеристик квантовых фазовых переходов в апериодических структурах остается сложной задачей. В работе ‘Quantum Hyperuniformity and Quantum Weight’ предложен новый подход, основанный на концепции квантовой гиперuniformности, для характеристики квантовых состояний и переходов, проявляющихся в подавлении длинноволновых квантовых флуктуаций. Показано, что различные фазы, включая состоящие с разрывом в спектре, безразрывные и локализованные критические, могут быть четко дифференцированы на основе классов квантовой гиперuniformности, а величина разрыва в спектре количественно оценивается через квантовый вес. Каким образом предложенный подход может быть расширен для анализа более сложных многочастичных систем и обнаружения новых квантовых явлений?
За гранью беспорядка: Рождение локализованных состояний
В квантовых системах с беспорядком наблюдается нарушение общепринятых представлений о распространении волновых функций. Вместо ожидаемого рассеяния и девиации, происходит переход к локализации, когда волновая функция, описывающая состояние частицы, оказывается “запертой” в определенной области пространства. Этот феномен, известный как локализация, возникает из-за случайного расположения дефектов или примесей в материале, что приводит к интерференции волновых функций и подавлению их распространения. Ψ(x) → 0 за пределами локализованной области. Данное явление принципиально отличается от классического хаоса и имеет значительные последствия для понимания свойств материалов, особенно в контексте разработки новых квантовых устройств и материалов с необычными электронными свойствами.
Понимание переходов к локализации во многих телах имеет первостепенное значение для создания принципиально новых квантовых материалов с заданными свойствами. Эти переходы, определяющие, как квантовые частицы ведут себя в хаотичных системах, позволяют контролировать транспорт энергии и информации на квантовом уровне. Изучение этих явлений открывает путь к разработке материалов, устойчивых к декогеренции — разрушению квантовых состояний — что является ключевым требованием для создания стабильных квантовых компьютеров и других квантовых устройств. Более того, исследование механизмов, лежащих в основе этих переходов, способствует углублению фундаментального понимания квантовой механики и ее проявлений в сложных системах, расширяя границы нашего знания о природе материи и ее возможностях. По сути, понимание локализации многочастичных систем — это не только технологический прорыв, но и углубление в основы физической реальности.
Традиционные методы анализа квантовых систем, испытывающих сильное беспорядочное воздействие, оказываются недостаточно эффективными для полного описания сложного взаимодействия между хаотичностью и квантовыми эффектами. Это связано с тем, что стандартные подходы, разработанные для идеальных, упорядоченных систем, не способны адекватно учесть экспоненциальный рост сложности, возникающий при наличии случайных возмущений. Например, при попытке моделирования энергетических спектров в сильно локализованных системах, стандартные численные методы сталкиваются с огромными вычислительными затратами, а приближения часто оказываются неточными. Более того, анализ корреляционных функций и других ключевых характеристик системы затрудняется из-за нетривиальной структуры волновых функций и их чувствительности к мельчайшим изменениям в беспорядке. Поэтому, для углубленного понимания феномена множественной локализации и разработки новых квантовых материалов, требуются инновационные теоретические и вычислительные подходы, способные преодолеть эти ограничения.
Квантовая гиперупорядоченность: Новая перспектива порядка
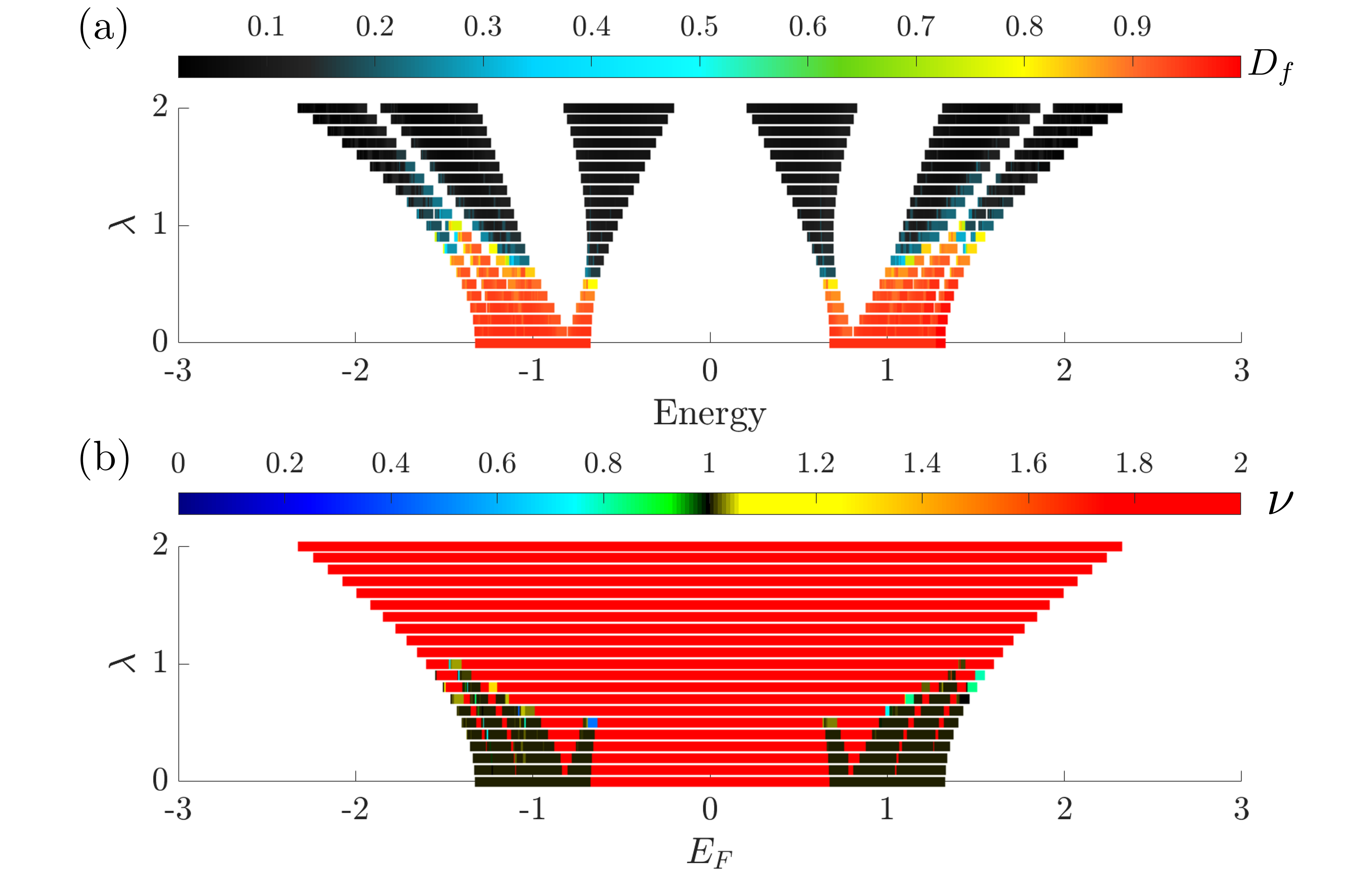
Квантовая гиперупорядоченность (КГУ) представляет собой мощный подход к выявлению порядка в системах, где отсутствует традиционная кристаллическая симметрия. В отличие от классических упорядоченных структур, характеризующихся периодическим расположением частиц, КГУ проявляется через подавление флуктуаций плотности вероятности, что обнаруживается анализом структуры фактора плотности заряда. Данный подход позволяет идентифицировать упорядоченное поведение в апериодических системах, таких как квазикристаллы или аморфные материалы, где стандартные методы анализа кристаллической структуры неприменимы. S(q) \rightarrow 0 при q \rightarrow 0 является характерным признаком КГУ, указывающим на отсутствие флуктуаций плотности в пределе длинных волн.
Квантовая гиперуниформность (КГУ) характеризуется подавлением флуктуаций плотности, что означает, что распределение частиц в системе отклоняется от случайного более, чем можно было бы ожидать. Количественно оценить степень подавления флуктуаций плотности позволяет функция структуры плотности заряда S(q). Эта функция описывает, как быстро осциллирует плотность заряда при различных волновых векторах q. В гиперуниформных системах S(q) подавляется при малых q, демонстрируя отсутствие пиков, которые обычно встречаются в кристаллических структурах, и остаётся подавленной даже в отсутствие дальнего порядка. Фактически, отсутствие пиков в S(q) является ключевым индикатором КГУ, позволяющим отличить гиперуниформные системы от обычных случайных сред.
Модель Обри-Андре является ключевой платформой для изучения возникновения квантовой гиперупорядоченности (QHU) вблизи переходов к локализации. Данная модель, описывающая поведение электронов в периодическом потенциале с дефектами, демонстрирует подавление флуктуаций плотности вероятности, что является характерным признаком QHU. В частности, анализ функции структуры плотности заряда S(q) для системы, описываемой моделью Обри-Андре, показывает, что вблизи перехода к локализации наблюдается подавление значений S(q) при малых значениях q, что количественно подтверждает наличие гиперупорядоченности, несмотря на отсутствие дальнодействующего порядка.
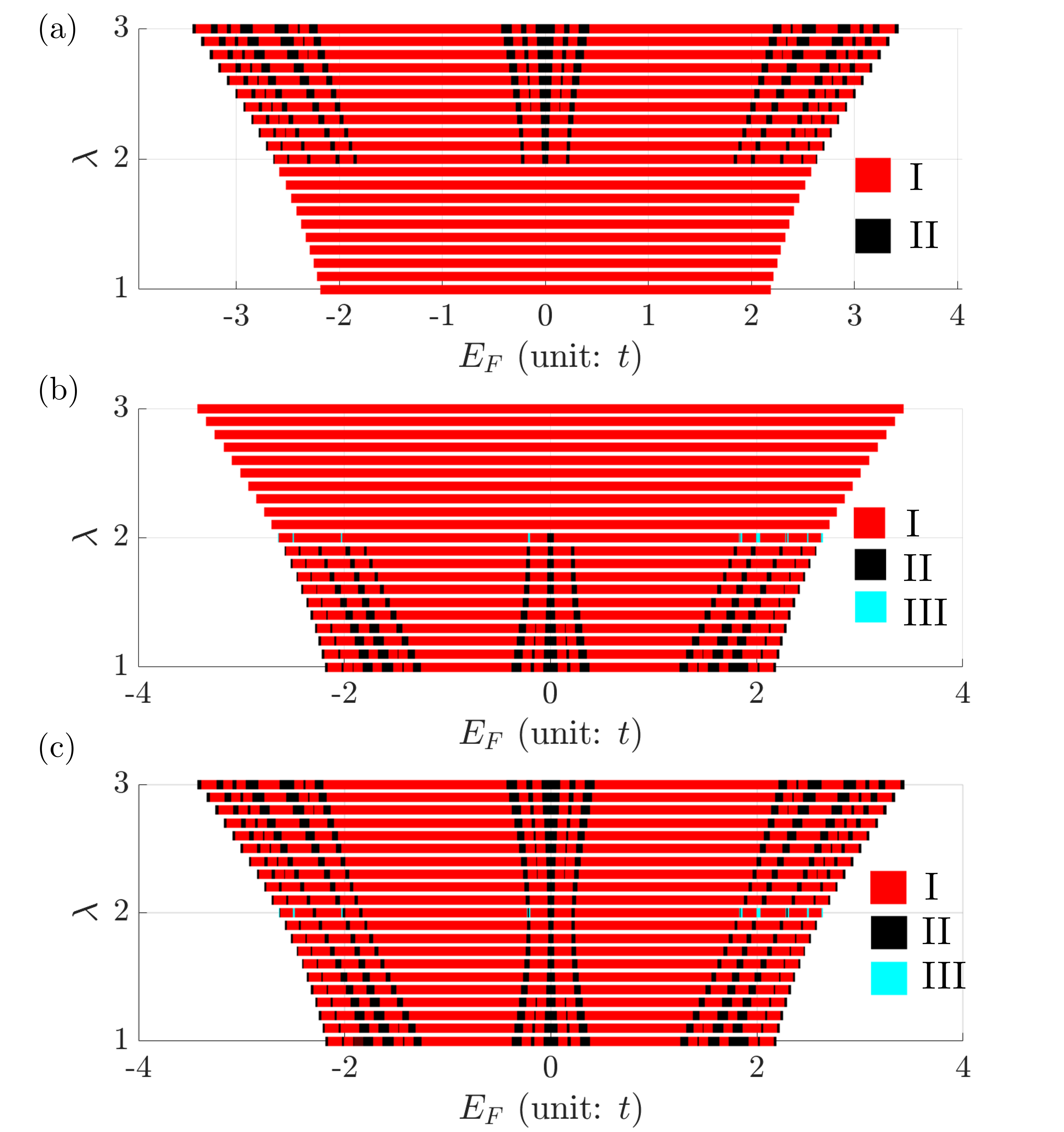
Расшифровка критичности с помощью гиперупорядоченности и масштабирования
В критических фазах показатель масштабирования ν напрямую связан с поведением фактора структуры плотности заряда в квазигармонических упорядоченных (QHU) системах. В QHU системах данный показатель может варьироваться в диапазоне меньше 1, больше 1, и принимать значение, равное 2, в определенных фазах. Значение ν определяет характер распада корреляционных функций вблизи критической точки, и его связь с фактором структуры плотности заряда предоставляет метод характеризации критической фазы и определения ее параметров посредством анализа масштабирования.
Квантово-хаотическая униформа (QHU) позволяет не только определить переход к локализации, но и характеризовать критическую фазу посредством анализа масштабирования. В критической точке система демонстрирует фрактальные свойства, которые проявляются в поведении структуры фактора плотности заряда. Анализ поведения этого фактора позволяет определить критический индекс масштабирования ν, который является ключевой характеристикой критической фазы и может принимать значения меньше 1, больше 1 или равняться 2 в зависимости от конкретной фазы. Это масштабирование, в свою очередь, предоставляет информацию о корреляционной длине и фрактальной размерности системы в критическом состоянии, что позволяет детально описать свойства критической фазы.
Комбинирование квантовой гиперупорядоченности (QHU) с обратным коэффициентом участия (IPR) позволяет получить более глубокое понимание локализации волновой функции. Установлена связь между размером энергетической щели и квантовым весом (K) посредством соотношения: Размер щели ∝ K^{-β}, где β ≈ 0.7153. Использование IPR позволяет количественно оценить степень локализации волновой функции, а QHU предоставляет информацию о корреляциях в системе, что в совокупности дает возможность более точно определить параметры, характеризующие критическую фазу и ее чувствительность к изменениям в системе.
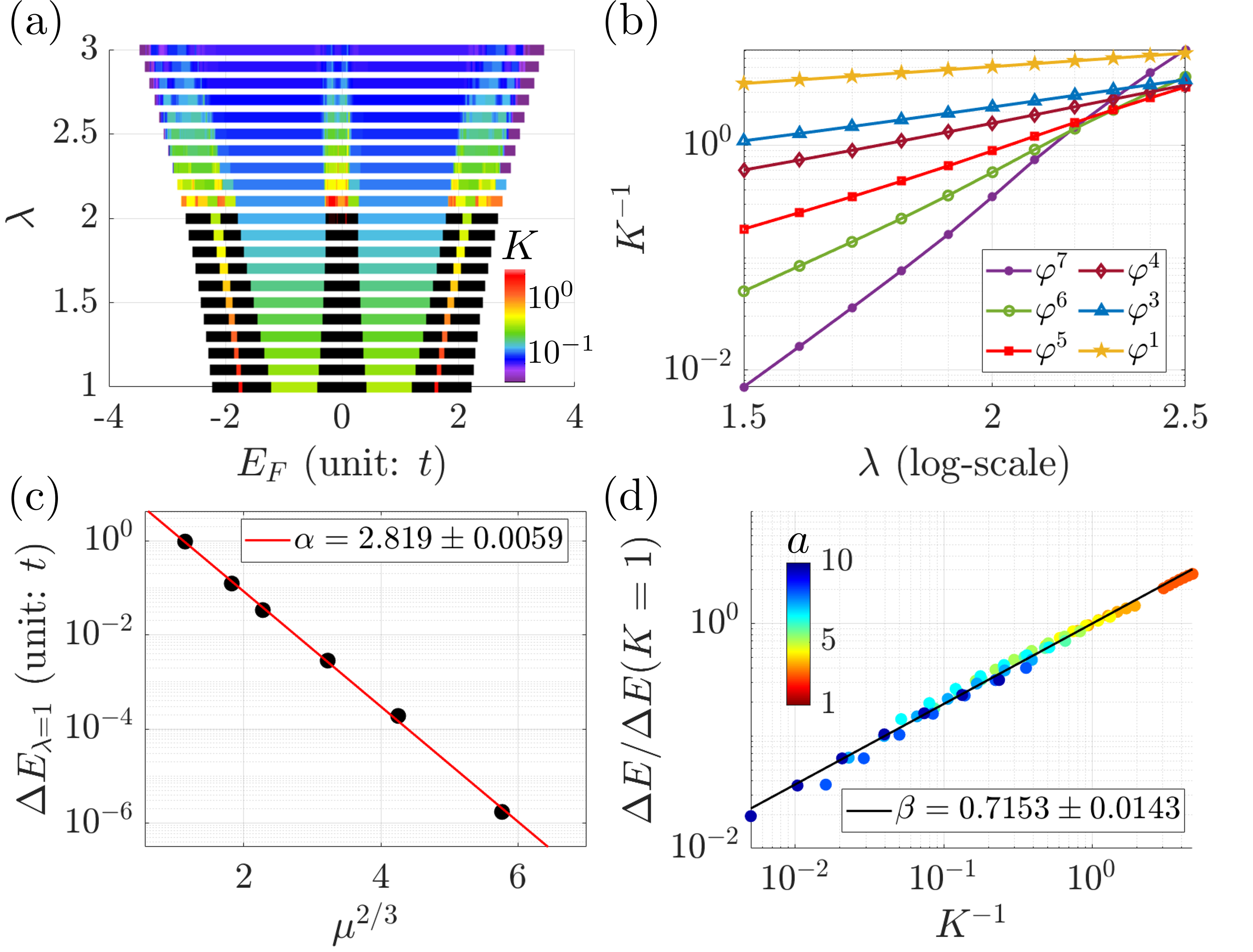
От локализации к универсальным квантовым фазам
Принципы квантового хаоса в упорядоченных системах (QHU) и связанные с ними закономерности масштабирования оказываются применимы не только к системам с беспорядком, но и к более сложным квантовым фазам материи, в том числе к тем, которые характеризуются дробной размерностью, например, к системам с фрактальной геометрией. Исследования показывают, что универсальные характеристики, определяемые QHU, проявляются и в этих сложных фазах, позволяя выявлять общие закономерности в поведении электронов и других квазичастиц. Это означает, что методы, разработанные для изучения локализации в беспорядоченных системах, могут быть успешно применены для понимания свойств более экзотических материалов и предсказания их характеристик, что открывает новые возможности для материаловедения и создания устройств нового поколения.
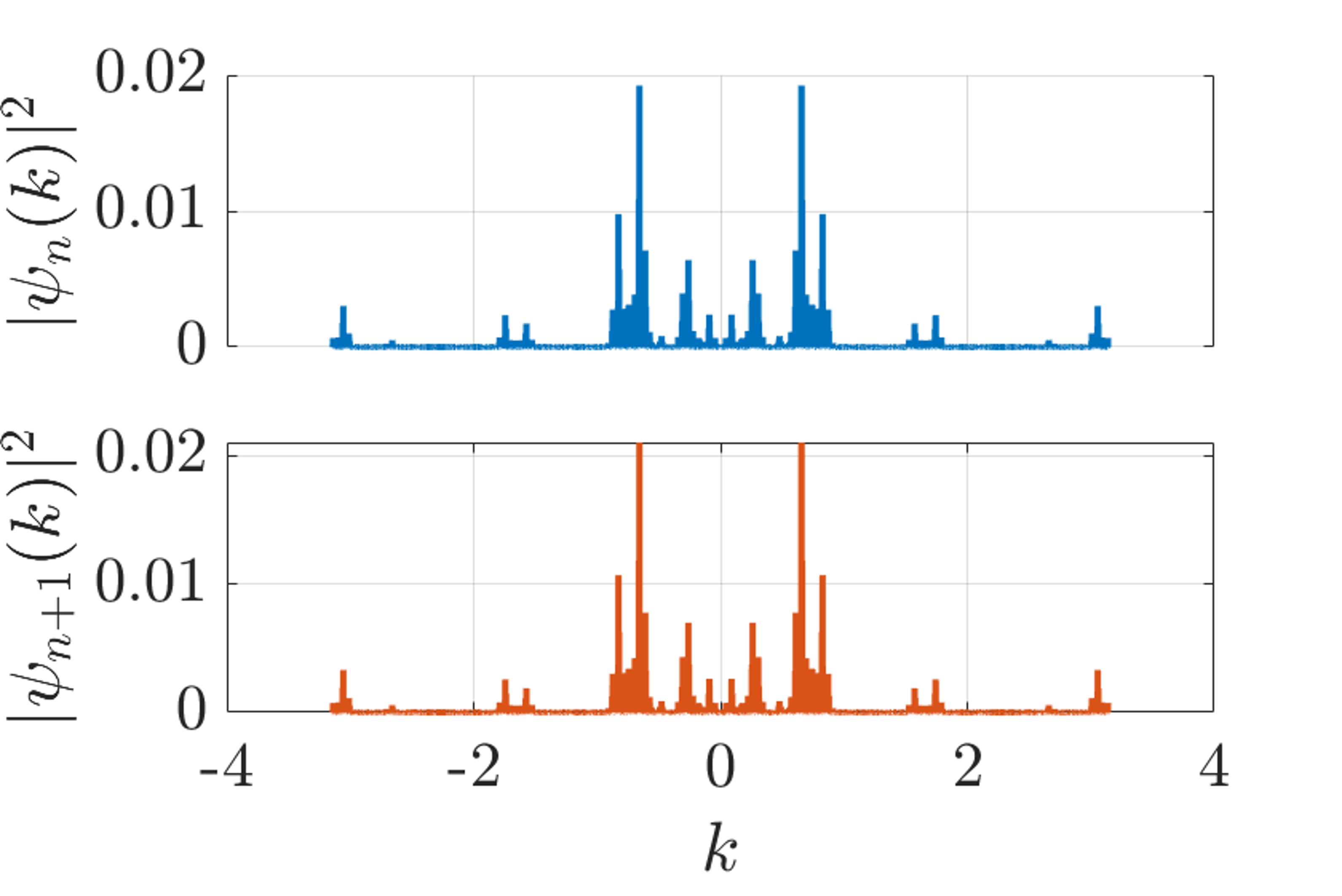
Исследование взаимосвязи между универсальностью вблизи хаотических состояний (QHU), локализацией и структурой волновых функций в импульсном пространстве открывает принципиально новые возможности для разработки материалов с заданными свойствами. Понимание того, как эти факторы влияют на поведение электронов в твердых телах, позволяет предсказывать и контролировать такие характеристики, как проводимость и сверхпроводимость. В частности, анализ структуры волновых функций в импульсном пространстве выявляет критические точки, определяющие фазовые переходы и появление экзотических квантовых состояний. Используя эти знания, ученые могут целенаправленно конструировать материалы с улучшенными или совершенно новыми функциональными возможностями, например, высокоэффективные солнечные элементы или квантовые вычислительные устройства, где контроль над локализацией и когерентностью электронов является ключевым.
Исследования показали, что квантовый вес (K) играет ключевую роль в предсказании энергетической щели в материалах. Установлена прямая связь, описываемая соотношением ΔE ∝ e^{-αμ²/³}, где ΔE представляет собой величину энергетической щели, а μ — параметр, связанный с квантовым весом. Данная зависимость позволяет оценивать электронные свойства материалов, не прибегая к сложным вычислительным методам. Чем больше квантовый вес, тем меньше энергетическая щель, что указывает на более высокую проводимость. Использование этого соотношения открывает перспективы для целенаправленного дизайна новых материалов с заданными электрическими характеристиками, представляя собой мощный инструмент в материаловедении и физике твердого тела.
За пределами беспорядка: Будущее квантовой гиперупорядоченности
Классическая гиперупорядоченность (КГУ) представляет собой концепцию, тесно связанную с квантовой гиперупорядоченностью (КГУ), и служит более широкой основой для понимания пространственных корреляций в различных системах. В то время как КГУ описывает упорядоченность, возникающую из классических взаимодействий, КГУ расширяет эту концепцию, охватывая упорядоченность, обусловленную квантовыми эффектами. Изучение взаимосвязи между этими двумя формами гиперупорядоченности позволяет рассматривать широкий спектр систем, от простых классических жидкостей до сложных квантовых материалов, в рамках единого формального подхода. Такое объединение позволяет выявлять общие принципы, определяющие появление долгосрочных корреляций, и предсказывать новые формы упорядоченности, не наблюдаемые в классических системах. Наличие КГУ как более широкой основы для понимания КГУ значительно расширяет возможности анализа и проектирования материалов с заданными свойствами, позволяя преодолеть ограничения, связанные исключительно с квантовыми или классическими моделями.
Исследование взаимосвязи между квантовой гиперравномерностью и более экзотическими квантовыми состояниями открывает новые перспективы в понимании природы порядка и сложности. Ученые предполагают, что изучение систем, находящихся в необычных квантовых состояниях, таких как конденсат Бозе-Эйнштейна или топологические фазы материи, в сочетании с принципами квантовой гиперупорядоченности g(r) = 0 для r \neq 0, позволит выявить ранее неизвестные формы упорядоченности, выходящие за рамки традиционных представлений о кристаллах и аморфных структурах. Такой подход может раскрыть фундаментальные связи между квантовой запутанностью, пространственными корреляциями и макроскопическими свойствами материи, углубляя наше понимание о том, как сложность возникает из простых квантовых принципов и открывая пути к созданию материалов с уникальными и непредсказуемыми характеристиками.
Применение принципов квантовой гиперупорядоченности открывает захватывающие перспективы в материаловедении, потенциально приводя к созданию принципиально новых квантовых материалов. Исследования показывают, что оптимизация пространственного расположения частиц на квантовом уровне может значительно улучшить эффективность хранения энергии, увеличив плотность и скорость зарядки аккумуляторных устройств. Более того, гиперравномерные структуры демонстрируют уникальные когерентные свойства, необходимые для создания стабильных и масштабируемых кубитов — основных строительных блоков квантовых компьютеров. Использование данных принципов позволит проектировать материалы с улучшенной проводимостью, повышенной чувствительностью к внешним воздействиям и, как следствие, совершить прорыв в области квантовых вычислений и разработки передовых сенсоров.
Изучение квантовой гиперуниформности, представленное в данной работе, напоминает о хрупкости любого порядка. Авторы стремятся выявить критические состояния и фазовые переходы через подавление квантовых флуктуаций, что неизбежно ведет к осознанию: порядок — это лишь временный кэш между сбоями. В этом контексте приходят на ум слова Джона Локка: «Все знания — это опыт». Подобно тому, как Локк подчеркивал важность эмпирического наблюдения, данное исследование стремится понять квантовые системы через их наблюдаемые свойства, а именно, через анализ структуры фактора и выявление новых фаз материи. Каждая новая архитектура, будь то квантовая система или программный код, обещает свободу, пока не потребует жертв — в данном случае, понимания пределов подавления квантовых флуктуаций.
Что Дальше?
Представленное исследование, касающееся квантовой гиперуниформности, открывает не столько набор инструментов для классификации фаз, сколько намекает на необходимость пересмотра самого понятия “фазы”. Попытка описать квантовые состояния через подавление долговолновых флуктуаций — это, по сути, признание нашей неспособности предсказать, где именно проявится следующий момент истины. Настоящая устойчивость системы, как и истинное понимание её поведения, рождается не из уверенности в контроле, а из осознания неизбежности неожиданного.
Очевидным ограничением подхода является его зависимость от конкретных моделей — в частности, от анализа структуры фактора. Однако, более глубокая проблема кроется в самой идее поиска “порядка” в квантовом мире. Не является ли стремление к гиперуниформности лишь очередным способом навязать классические представления системам, которые по определению не поддаются такому описанию? Возможно, в будущем, следует сосредоточиться не на поиске универсальных критериев, а на разработке методов анализа, позволяющих описывать уникальные траектории эволюции каждой конкретной системы.
Перспективы использования квантовой гиперуниформности в изучении квазипериодических систем, таких как модель Обри-Андре, выглядят многообещающе. Однако, истинный вызов заключается в расширении этого подхода на более сложные системы с сильными взаимодействиями и нетривиальной топологией. Именно там, в области хаоса и неопределенности, и кроется ключ к пониманию фундаментальных принципов, управляющих квантовым миром. Мониторинг же — это лишь осознанный способ бояться.
Оригинал статьи: https://arxiv.org/pdf/2601.18331.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip
- Все рецепты культистского круга в Escape from Tarkov
- Решение головоломки с паролем Absolum в Yeldrim.
- Лучшие шаблоны дивизий в Hearts Of Iron 4
- Лучшие транспортные средства в Far Cry 6
- Необходимо: Как выращивать урожай
- Где найти и поймать бабочку Солнечного луча в Палии
- All Valley Pass Aurylene Locations In Endfield
- Dragon’s Dogma 2: Где найти Драконорожденных
- Warhorse говорит, что им пришлось отказаться от исторической точности для системы преступлений в Kingdom Come: Deliverance, так как это было бы ‘слишком сурово’ для ‘крестьянского парня’ Генри – ‘Любое преступление каралось бы очень строго’.
2026-01-27 19:13