Квантовая гравитация: Геометрия из масштаба

Автор: Денис Аветисян

Новая теоретическая модель предполагает, что структура пространства-времени возникает из динамики локальных измерений масштаба и квантовых флуктуаций.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал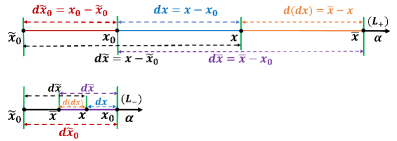

При измерении микроскопических флуктуаций пространства-времени, направление этих флуктуаций определяется знаком среднего значения <span class="katex-eq" data-katex-display="false">\bar{X}^{\alpha}_{0}</span>: если <span class="katex-eq" data-katex-display="false">\bar{X}^{\alpha}_{0}</span> отрицательно при <span class="katex-eq" data-katex-display="false">X^{\alpha}</span> больше нуля, и соблюдаются условия <span class="katex-eq" data-katex-display="false">\bar{X}^{\alpha}_{0}/2 < L_{-} \leq \bar{X}^{\alpha}_{0}</span> и <span class="katex-eq" data-katex-display="false">L_{+} \geq \bar{X}^{\alpha}_{0}</span>, то флуктуации направлены в одну сторону, а при положительном <span class="katex-eq" data-katex-display="false">\bar{X}^{\alpha}_{0}</span> - в противоположную. — При измерении микроскопических флуктуаций пространства-времени, направление этих флуктуаций определяется знаком среднего значения $\bar{X}^{\alpha}_{0}$ : если $\bar{X}^{\alpha}_{0}$ отрицательно при $X^{\alpha}$ больше нуля, и соблюдаются условия $\bar{X}^{\alpha}_{0}/2 < L_{-} \leq \bar{X}^{\alpha}_{0}$ и $L_{+} \geq \bar{X}^{\alpha}_{0}$ , то флуктуации направлены в одну сторону, а при положительном $\bar{X}^{\alpha}_{0}$ — в противоположную.

Предлагается подход к квантованию пространства-времени, основанный на масштабируемых многообразиях и обобщенном принципе неопределенности.

Классическое представление о пространстве-времени как о гладком континууме сталкивается с трудностями при попытке согласования с квантовой механикой. В работе ‘Scaling-Based Quantization of Spacetime Microstructure’ предложен новый подход к квантованию гравитации, основанный на масштабируемых степенях свободы, где локальные факторы масштаба выступают фундаментальными динамическими переменными. Данная конструкция приводит к дискретности пространства-времени на микроскопическом уровне и предполагает геометрический поток ренормализационной группы для переменных масштаба, а также обобщенное соотношение неопределенности с коэффициентами, зависящими от масштаба. Может ли предложенная теория стать основой для решения космологической проблемы постоянной и предсказания новых физических явлений, связанных с квантовой структурой пространства-времени?

Флуктуации Пространства-Времени: Основа Новой Физики

Современные физические модели пространства-времени, как правило, оперируют представлением о нём как о гладкой и непрерывной структуре. Однако, на планковском масштабе — чрезвычайно малых расстояниях порядка $10^{-{35}}$ метров — эта концепция может оказаться неточной. Теоретические изыскания указывают на возможность существования значительных квантовых флуктуаций, искажающих геометрию пространства-времени. Эти флуктуации, если они действительно существуют, представляют собой не просто незначительные отклонения, а фундаментальные изменения в самой ткани реальности, способные влиять на распространение света и гравитационные взаимодействия. Представление о гладком пространстве-времени, таким образом, может являться лишь приближением, справедливым на макроскопических масштабах, скрывающим более сложную и динамичную картину на самом фундаментальном уровне.

Если флуктуации пространства-времени действительно существуют, это потребует пересмотра основополагающих понятий о расстоянии, площади и энергии. Традиционные представления о геометрии, где эти величины считаются абсолютными и неизменными, окажутся неточными на планковском масштабе. Вместо фиксированных значений, расстояние и площадь приобретут вероятностный характер, представляя собой не единые числа, а распределения вероятностей. Энергия, как мера работы, также станет подвержена флуктуациям, что повлияет на понимание сохранения энергии и может привести к новым интерпретациям космологических процессов, таких как инфляция и темная энергия. Представление о пространстве-времени как о гладком континууме уступит место модели, в которой оно состоит из «зернистой» структуры, где даже самые малые измерения подвержены неопределенности, что открывает возможности для новых физических теорий и экспериментов.

Предполагается, что включение флуктуаций пространства-времени в существующие теоретические модели способно разрешить давние парадоксы, возникающие на стыке квантовой механики и общей теории относительности. В частности, это может привести к более полному пониманию сингулярностей, возникающих в чёрных дырах и в момент Большого взрыва, предлагая механизм, предотвращающий их формирование. Более того, флуктуации пространства-времени могут объяснить природу тёмной энергии и тёмной материи, представляя собой альтернативу гипотетическим частицам и полям. Исследования в этом направлении предполагают, что само пространство-время не является статичной ареной, а динамической сущностью, подверженной квантовым колебаниям, что, в свою очередь, влияет на гравитационные взаимодействия и эволюцию Вселенной. В конечном итоге, такая модель может объединить все фундаментальные силы природы в единую теорию, устраняя необходимость в отдельных описаниях для каждой из них.

В рамках исследования флуктуаций пространства-времени предложена теоретическая конструкция, использующая так называемые “Коэффициенты масштаба” для моделирования возникающих искажений. Эти коэффициенты, представляющие собой локальные отклонения от привычных единиц измерения, позволяют описывать изменения метрики пространства-времени на планковском масштабе. $S(x)$ — функция, определяющая масштабный фактор в точке $x$ , позволяет количественно оценить степень деформации пространства в данной области. Предложенный подход предполагает, что пространство-время не является гладким континуумом, а состоит из постоянно меняющихся, флуктуирующих единиц, и что эти флуктуации являются фундаментальной характеристикой реальности, способной разрешить противоречия между квантовой механикой и общей теорией относительности. Использование коэффициентов масштаба открывает возможность построения более точных моделей ранней Вселенной и черных дыр, учитывающих квантовые эффекты гравитации.

Многообразие Первого Порядка: Геометрия Флуктуаций

В качестве базовой геометрии предлагается ‘Многообразие первого порядка’, включающее в себя ‘Коэффициенты масштаба’ для представления локальных искажений пространства-времени. Данное многообразие служит основой для описания геометрии, где пространство-время не является статичным, а подвержено флуктуациям, отражающимся в изменении метрики. Коэффициенты масштаба, являющиеся функциями координат, позволяют моделировать деформации пространства-времени в различных точках, определяя локальные изменения расстояний и кривизны. Использование коэффициентов масштаба позволяет описывать как гравитационные волны, так и другие формы динамических искажений, возникающих под влиянием распределения массы и энергии. $\mathcal{M}_1$ обозначает это многообразие, где локальная метрика $\tilde{g}_{\mu\nu}$ определяется как произведение метрики базового многообразия $g_{\mu\nu}$ и коэффициентов масштаба $\alpha(x)$ .

Многообразие первого порядка использует так называемую ‘скалированную метрику’ для определения расстояний и кривизн, что позволяет отразить флуктуирующий характер пространства-времени. В отличие от стандартной римановой метрики, скалированная метрика включает в себя локальные ‘коэффициенты масштаба’, которые изменяются в каждой точке пространства-времени. Это приводит к тому, что длина дуги $ds$ вычисляется как $ds = \sqrt{g_{\mu\nu}(x) dx^\mu dx^\nu}$ , где $g_{\mu\nu}(x)$ — тензор метрики, зависящий от координат $x$ . Изменение этих коэффициентов масштаба влияет на измерение расстояний и, следовательно, на вычисление кривизны, отражая тем самым динамическую природу пространства-времени и позволяя описывать локальные искажения.

Вводится понятие второго порядка многообразия, представляющего собой пространство амплитуд факторов масштабирования. Данное многообразие необходимо для полного геометрического описания системы, поскольку факторы масштабирования, определяющие локальные искажения пространства-времени, сами по себе могут изменяться. Пространство амплитуд этих факторов масштабирования рассматривается как геометрическое пространство, параметризуемое соответствующими степенями свободы. Таким образом, второе многообразие дополняет первое, обеспечивая полное описание как геометрии пространства-времени, так и динамики его локальных искажений, представленных в виде факторов масштабирования. Амплитуды факторов масштабирования, определяющие величину этих искажений, являются координатами в данном многообразии.

Скалярный лагранжиан $\mathcal{L}$ предоставляет математическую основу для описания динамики рассматриваемой системы, определяя эволюцию как самой геометрии пространства-времени, так и флуктуаций масштабных факторов. Он включает в себя кинетическую энергию, связанную с изменением метрики первого порядка, а также потенциальную энергию, описывающую взаимодействия между масштабными факторами и их влиянием на кривизну пространства. Этот лагранжиан позволяет получить уравнения движения для метрических тензоров первого и второго порядка, определяя таким образом динамику масштабируемого многообразия и его влияние на локальную геометрию пространства-времени. Выбор конкретной формы лагранжиана определяется физическими предположениями о природе масштабных факторов и их взаимодействии с гравитацией.

Динамические Последствия: Модификация Фундаментальных Уравнений

Масштабный Лагранжиан оказывает непосредственное влияние на фундаментальные величины, определяющие геометрию пространства-времени, такие как тензор кривизны Римана $R_{ijkl}$ и символы Кристоффеля $\Gamma^i_{jk}$ . Изменение Лагранжиана приводит к модификации этих величин, что, в свою очередь, влечет за собой переопределение кривизны пространства-времени. В частности, введение масштабных факторов в Лагранжиан изменяет компоненты тензора кривизны и, соответственно, влияет на гравитационные взаимодействия и траектории движения объектов в искривленном пространстве-времени. Данная модификация является ключевым аспектом в изучении флуктуаций геометрии и их влияния на физические процессы.

Модификация уравнений Клейна-Гордона и Дирака посредством введения масштабных факторов приводит к изменению поведения релятивистских частиц. В частности, в уравнениях вводятся коэффициенты масштабирования, которые влияют на энергию и импульс частиц, описываемых этими уравнениями. Для уравнения Клейна-Гордона изменение выглядит как $(\partial_\mu + iA_\mu) (\partial^\mu + iA^\mu) \psi = m^2 \psi$ , где масштабные факторы включены в $A_\mu$ . Аналогично, в уравнении Дирака, $(i\gamma^\mu \partial_\mu - m) \psi = 0$ , масштабные факторы модифицируют матричные коэффициенты $\gamma^\mu$ и/или саму массу частицы $m$ . Это приводит к изменению волновых функций и, как следствие, вероятности обнаружения частиц, а также их скоростей и энергий в заданных условиях.

Уравнения геодезических адаптируются для учета флуктуаций пространства-времени посредством введения поправок, зависящих от изменений метрики. Это приводит к отклонению траекторий объектов от классических геодезических, описываемых в общей теории относительности. В частности, при наличии случайных флуктуаций метрики $g_{\mu\nu}$ , уравнения геодезических приобретают дополнительный член, описывающий влияние этих флуктуаций на ускорение объекта. Решение модифицированных уравнений геодезических показывает, что частицы испытывают случайные отклонения от своих первоначальных траекторий, что может привести к изменению их кинетической энергии и, в конечном итоге, к изменению динамики системы. Данная адаптация критически важна для анализа движения частиц в условиях квантовой гравитации и позволяет учесть эффекты, связанные с негладкостью пространства-времени на микроскопических масштабах.

Модальный разложение позволяет анализировать влияние факторов масштаба на разложение полей на моды. В результате этого разложения получаются квантованные моды, характеризующиеся собственными значениями $\omega_i^2 = k_i/m_i$ , где $\omega_i$ — частота моды, $k_i$ — волновое число, а $m_i$ — масса частицы, связанной с данной модой. Значения этих собственных значений напрямую определяют стабильность вакуума, поскольку положительные значения указывают на стабильные моды, а отрицательные — на нестабильные, приводящие к расходу энергии вакуума и, потенциально, к его распаду.

Квантовые Последствия: Энтропия и Энергия Нулевой Точки

Предлагаемая теоретическая структура оказывает существенное влияние на вычисление так называемой «энергии нулевой точки», что обусловлено модификацией геометрии пространства-времени на фундаментальном уровне. В отличие от традиционных подходов, рассматривающих плоское пространство, данная модель учитывает флуктуации масштабного фактора и искажения, возникающие из-за изменчивости геометрии. Это приводит к переоценке плотности вакуума и, как следствие, к изменению величины $E_0 = \frac{\hbar c}{2}$ , поскольку энергия нулевой точки становится чувствительной к специфическим свойствам искривленного пространства-времени. В результате, предложенный подход позволяет более точно моделировать квантовые эффекты в гравитационно активных областях и вносит вклад в понимание природы темной энергии, связывая её с квантовыми флуктуациями вакуума в искривленном пространстве.

Для описания площади на планковском масштабе был разработан так называемый ‘Микроскопический Оператор Площади’, который учитывает флуктуации масштабных факторов. Данный оператор не рассматривает площадь как фиксированную величину, а представляет ее как динамическую переменную, подверженную квантовым колебаниям. В рамках данной конструкции, масштабные факторы, определяющие геометрию пространства-времени на самых малых расстояниях, не являются постоянными, а претерпевают изменения, что напрямую влияет на вычисление площади. Учет этих флуктуаций позволяет более точно моделировать поведение пространства-времени на планковском уровне и, как следствие, корректно вычислять такие фундаментальные величины, как энтропия черных дыр, согласуясь с законом Бекенштейна-Хокинга $S_{BH} = A/(4l_p^2)$ , где $A$ — площадь горизонта событий, а $l_p$ — планковская длина.

Данная теоретическая структура позволяет воспроизвести энтропию Бekenштейна-Хокинга для чёрных дыр, устанавливая связь между микроскопической площадью и макроскопической термодинамикой посредством законa площади: $S_{BH} = A/(4l_p^2)$ . В рамках этого подхода, энтропия чёрной дыры рассматривается как функция от площади её горизонта событий, делённой на квадрат длины Планка. Это указывает на глубокую связь между гравитацией, квантовой механикой и термодинамикой, где площадь играет роль меры беспорядка или информации, содержащейся в чёрной дыре. Полученное соответствие подтверждает, что чёрные дыры являются термодинамическими объектами, обладающими температурой и энтропией, что существенно расширяет понимание природы пространства-времени и его связи с информацией.

Группа перенормировки масштаба определяет эволюцию факторов масштаба, оказывая существенное влияние на общее поведение рассматриваемой системы. В рамках данной модели, анализ показывает, что собственные значения, характеризующие изменения масштаба в различных направлениях, принимают конкретные значения в евклидовом пространстве. В частности, продольное собственное значение $\lambda_{time} = -(D-1) a_{iso}^4$ , а поперечное — $\lambda_{space}(∥) = D-1 a_{iso}^4$ и $\lambda_{space}(⊥) = 3(D-1) a_{iso}^4$ , где $D$ — размерность пространства, а $a_{iso}$ представляет собой изолированный фактор масштаба. Полученные результаты демонстрируют, как изменения масштаба влияют на геометрию пространства и, следовательно, на физические процессы, происходящие в нем, что открывает новые возможности для изучения квантовой гравитации и космологии.

Будущие Направления: Микро-Измерения и За Ее Пределами

Теоретическая структура, известная как ‘Микро-измерение’, представляет собой инновационный подход к исследованию пространства-времени на планковском масштабе, используя концепцию функций масштаба. Вместо непосредственного измерения чрезвычайно малых расстояний, эта методика фокусируется на анализе флуктуаций этих функций, что позволяет косвенно изучать структуру пространства-времени на самых фундаментальных уровнях. Используя математический аппарат, включающий анализ собственных значений и векторов, данная структура позволяет выявить особенности геометрии пространства-времени, которые проявляются на планковском уровне. $\lambda_{time} = -(D-1) a_{iso}^4$ , $\lambda_{space}(∥) = D-1 a_{iso}^4$ и $\lambda_{space}(⊥) = 3(D-1) a_{iso}^4$ — примеры уравнений, описывающих эти флуктуации и дающих представление о характере квантовой гравитации. Этот подход открывает новые возможности для понимания природы пространства-времени и, возможно, позволит разрешить некоторые из самых сложных вопросов современной физики.

В дальнейшем исследования будут сосредоточены на разработке экспериментальных методов для регистрации эффектов флуктуаций пространства-времени. Обнаружение этих микроскопических колебаний, предсказанных теорией, представляет собой серьезную технологическую задачу, требующую создания приборов с беспрецедентной чувствительностью. Предполагается использование интерферометров нового поколения, способных улавливать изменения в длине волны света, вызванные гравитационными флуктуациями, а также разработка методов анализа космического микроволнового фона для выявления следов квантовой структуры пространства-времени. Успешная реализация этих экспериментов позволит не только подтвердить или опровергнуть существующие теоретические модели, но и открыть новые горизонты в понимании фундаментальных свойств Вселенной, включая природу темной энергии и ускоренного расширения.

Квантование масштабных факторов в рамках ‘Пространства Фока’ представляет собой перспективный подход к изучению их квантовой природы. Исследователи предполагают, что рассмотрение этих факторов как квантовых операторов, действующих в пространстве Фока, позволит получить более полное описание флуктуаций пространства-времени на планковском масштабе. Такой формализм позволяет применять методы квантовой теории поля для анализа поведения этих масштабных факторов, что может привести к пониманию их спектральных свойств и корреляций. В частности, это может помочь в разработке теории, описывающей гравитационное поле как квантовое, и позволит исследовать возможность существования квантовых гравитационных эффектов, которые невозможно объяснить в рамках классической общей теории относительности. Рассмотрение масштабных факторов в пространстве Фока может также пролить свет на природу темной энергии и ускоренного расширения Вселенной, открывая новые пути для понимания фундаментальных свойств пространства и времени.

Предлагаемый подход, основанный на исследовании микроизмерений, потенциально способен пролить свет на природу тёмной энергии и ускоренного расширения Вселенной. Анализ пространства Минковского выявляет собственные значения, характеризующие флуктуации пространства-времени: $\lambda_{time} = -(D-1) a_{iso}^4$ , $\lambda_{space}(∥) = D-1 a_{iso}^4$ , и $\lambda_{space}(⊥) = 3(D-1) a_{iso}^4$ , где $a_{iso}$ представляет собой масштабный фактор. Эти значения, отражающие энергию вакуума, могут быть ключевыми для понимания причин ускоренного расширения, поскольку предполагают, что само пространство-время вносит вклад в общую энергию Вселенной. Дальнейшее изучение этих собственных значений может предоставить новые теоретические рамки для объяснения наблюдаемого доминирования тёмной энергии и ее влияния на космологическую эволюцию.

Представленная работа исследует фундаментальную дискретность пространства-времени, опираясь на концепцию масштабируемых многообразий. Авторы стремятся вывести геометрию пространства-времени из динамики локальных измерений масштаба и флуктуаций. Этот подход, в сущности, представляет собой попытку упростить сложность квантовой гравитации, сосредотачиваясь на базовых принципах измерения. Как однажды заметил Ричард Фейнман: «Если вы не можете объяснить что-то простыми словами, значит, вы сами этого не понимаете». Данное исследование, фокусируясь на масштабируемых степенях свободы, демонстрирует стремление к такой же ясности и фундаментальному пониманию природы пространства-времени, что и знаменитое изречение.

Что дальше?

Представленная работа, стремясь к описанию квантовой гравитации через масштабируемые степени свободы, неизбежно наталкивается на вопрос об истинной природе дискретности пространства-времени. Недостаточно просто постулировать её; необходимо разработать экспериментально проверяемые предсказания, выходящие за рамки абстрактных математических построений. Поиск связи между предложенным масштабируемым лагранжианом и наблюдаемыми феноменами, такими как аномалии в космическом микроволновом фоне или отклонения от классической общей теории относительности в экстремальных гравитационных полях, представляется задачей первостепенной важности.

Неизбежно возникает и вопрос о самосогласованности предлагаемого подхода. Упрощение, заключающееся в отказе от метрического тензора как фундаментальной переменной, требует тщательной проверки на предмет появления нефизических решений или противоречий с установленными принципами квантовой механики. Попытки включить в рассмотрение эффекты обратной связи между локальными измерениями масштаба и глобальной геометрией пространства-времени могут оказаться плодотворными, но требуют осторожного обращения с возникающими сложностями.

В конечном счете, успех подобного подхода зависит не от сложности математического аппарата, а от его способности к очищению. Убрать лишнее — вот истинная задача. Поиск наиболее лаконичного и элегантного описания квантовой гравитации, свободного от произвольных параметров и неопределенностей, представляется не просто научной задачей, но и эстетическим императивом.

Оригинал статьи: https://arxiv.org/pdf/2601.15649.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-24 00:20