Автор: Денис Аветисян
Новое исследование демонстрирует, как квантовая информация может просачиваться сквозь горизонт событий аналоговой черной дыры, приближая нас к разрешению парадокса потери информации.
Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.
Бесплатный телеграм-канал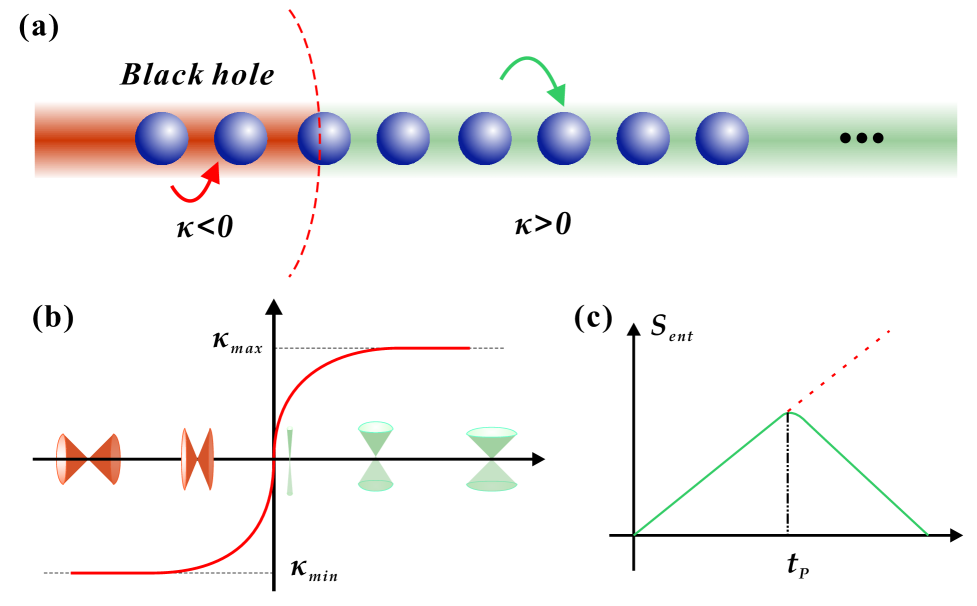
В работе показано, что XY спиновая цепь может имитировать поведение, подобное кривой Пейджа, и переносить квантовое запутывание и когерентность, предлагая возможный механизм решения парадокса потери информации в черных дырах.
Информационный парадокс чёрных дыр, ставящий под вопрос фундаментальные принципы сохранения информации в квантовой механике, остаётся одной из главных загадок современной физики. В работе, озаглавленной ‘Escape of quantum information across an analogue black hole horizon’, исследуется перенос квантовой информации в аналоговой модели чёрной дыры, реализованной на основе спиновой цепочки XY. Показано, что квантовые ресурсы, такие как запутанность и когерентность, могут передаваться через эффективный горизонт событий, демонстрируя поведение, аналогичное кривой Пейджа. Каким образом подобные исследования аналоговых систем могут пролить свет на механизмы выхода информации из настоящих чёрных дыр и разрешить давний парадокс?
Парадокс Черных Дыр: Где Скрывается Информация?
Парадокс потери информации в чёрных дырах возникает из-за кажущегося исчезновения информации, когда излучение Хокинга уносит энергию в пространство. Согласно квантовой механике, информация не может быть уничтожена, но процесс испарения чёрной дыры через излучение Хокинга предполагает, что детали о материи, попавшей внутрь, безвозвратно теряются. Это противоречие ставит под вопрос фундаментальные принципы физики, поскольку излучение Хокинга выглядит как тепловое, то есть не содержит информации о первоначальном состоянии коллапсировавшей звезды. Таким образом, процесс, описываемый теоретически, приводит к нарушению законов сохранения информации, что требует пересмотра существующих моделей гравитации и квантовой механики для согласования этих двух столпов современной физики.
Принцип унитарности, краеугольный камень квантовой механики, утверждает, что эволюция квантовой системы должна сохранять информацию о её начальном состоянии. Однако, возникновение излучения Хокинга, испускаемого чёрными дырами, представляется нарушением этого принципа. По мере испарения чёрной дыры, информация, которая когда-то содержалась в веществе, поглощённом ею, кажется, необратимо теряется с потоком излучения. Это противоречие ставит под сомнение фундаментальные основы нашего понимания гравитации и квантовой механики, поскольку предполагает, что информация может быть уничтожена, что недопустимо в рамках квантовой теории. Решение данной проблемы требует пересмотра существующих моделей и поиска новых теоретических подходов, способных согласовать принципы квантовой механики с теорией гравитации.
Для понимания того, как информация может покидать чёрную дыру или сохраняться в ней, необходимо глубокое осмысление квантовой запутанности между её внутренностью и внешней средой. Предполагается, что информация, попадающая в чёрную дыру, не уничтожается, а кодируется в корреляциях между излучением Хокинга и состоянием её внутреннего пространства. Данная запутанность может служить своего рода «каналом», по которому информация, хоть и искажённая, постепенно высвобождается, избегая нарушения фундаментальных законов квантовой механики. Изучение этой взаимосвязи требует разработки новых теоретических моделей, способных описать поведение гравитации и квантовых явлений на экстремальных масштабах, и может открыть путь к созданию последовательной теории квантовой гравитации.
Разрешение парадокса информационного исчезновения в чёрных дырах является фундаментальной необходимостью для построения последовательной теории квантовой гравитации. Существующие модели, объединяющие общую теорию относительности и квантовую механику, сталкиваются с принципиальными трудностями при описании поведения информации вблизи сингулярности чёрной дыры. Потеря информации, подразумеваемая испарением чёрной дыры посредством излучения Хокинга, противоречит базовым принципам квантовой механики, в частности, принципу унитарности. Поэтому, поиск механизма сохранения информации, будь то через тонкие эффекты в излучении Хокинга, нелокальные корреляции или радикальное переосмысление структуры пространства-времени, имеет решающее значение. Успешное разрешение парадокса не только позволит согласовать две фундаментальные теории физики, но и углубит понимание самой природы информации и её роли во Вселенной. Без этого, построение непротиворечивой теории квантовой гравитации, способной описывать самые экстремальные условия во Вселенной, остаётся невозможным.
Запутанность как Ключ к Сохранению Информации
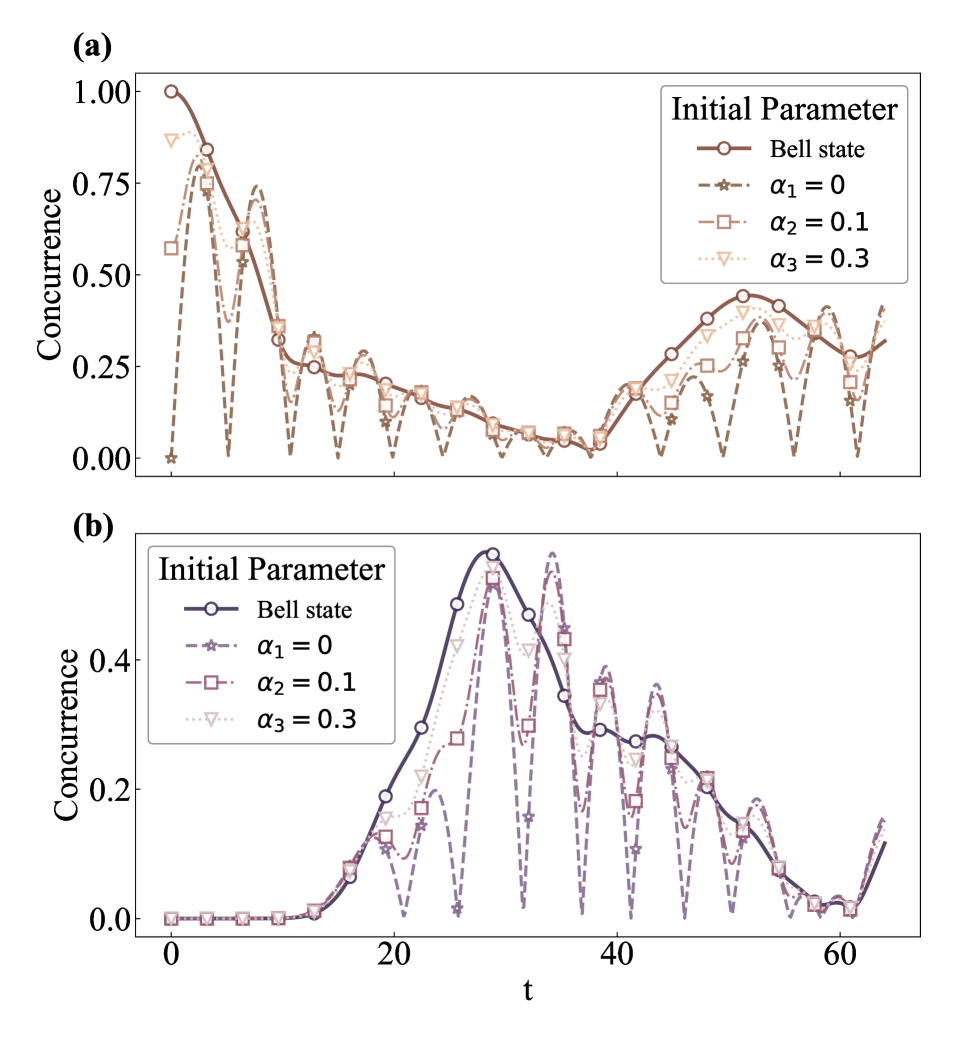
Квантовая запутанность, представляющая собой корреляцию между частицами, предлагает потенциальный механизм для сохранения информации. Вместо того, чтобы информация действительно терялась при попадании в черную дыру, она претерпевает “перемешивание” и кодируется в этих корреляциях. Это означает, что информация о состоянии вещества, поглощенного черной дырой, не уничтожается, а распределяется между запутанными частицами, составляющими излучение Хокинга. Таким образом, хотя доступ к исходному состоянию может быть затруднен, информация, принципиально, сохраняется в корреляциях между частицами, что позволяет рассматривать данное явление как процесс кодирования, а не уничтожения информации.
Количество запутанности между черной дырой и излучением Хокинга количественно оценивается с помощью энтропии запутанности, что обеспечивает измеримую связь между состоянием черной дыры и ее эволюцией. Данная величина позволяет отслеживать изменение запутанности во времени, и в начальные моменты существования черной дыры наблюдаемое поведение соответствует теоретическим предсказаниям, основанным на принципах квантовой механики и общей теории относительности. Измерение энтропии запутанности позволяет верифицировать модели, описывающие информационные процессы вблизи горизонта событий и подтвердить гипотезу о том, что информация, попадающая в черную дыру, не теряется полностью, а кодируется в корреляциях между частицами излучения Хокинга и самой черной дырой.
Соответствие AdS/CFT (Anti-de Sitter/Conformal Field Theory) представляет собой теоретическую конструкцию, предполагающую эквивалентность квантовой гравитации в определенных пространствах (пространствах Анти-де Ситтера) квантовой теории поля, лишенной гравитации. В рамках этого соответствия, информация, которая, казалось бы, исчезает при попадании в черную дыру, на самом деле сохраняется в виде степеней свободы на границе этого пространства. Это означает, что все физические процессы, происходящие в объеме пространства Анти-де Ситтера, могут быть полностью описаны квантовой теорией поля на его границе, обеспечивая механизм сохранения информации, который обходит парадокс потери информации в черных дырах. Математически, соответствие AdS/CFT устанавливает дуальность между гравитационным описанием в объеме и конформной теорией поля на границе, позволяя переносить расчеты между этими двумя, казалось бы, разными системами.
В рамках соответствия AdS/CFT информация о внутреннем состоянии черной дыры кодируется в корреляциях, определяемых запутанностью квантовой полевой теории, существующей на границе пространства-времени. Данный подход предполагает, что все степени свободы, необходимые для описания информации, падающей в черную дыру, проявляются в виде запутанности между граничной полевой теорией и микросостояниями черной дыры. Измерение степени запутанности, выраженной через энтропию запутанности, позволяет получить информацию о структуре и состоянии внутренних областей черной дыры, избегая тем самым нарушения принципа сохранения информации. По сути, информация не исчезает в черной дыре, а перераспределяется и кодируется в корреляциях между частицами на границе.
Моделирование Черных Дыр с Помощью Спиновых Цепей
Цепь XY, представляющая собой модель взаимодействующих спинов, используется в качестве аналога искривленного пространства-времени, позволяя исследователям моделировать эффекты, возникающие вблизи чёрных дыр. В данной модели каждый спин соответствует точке в пространстве-времени, а взаимодействие между спинами имитирует гравитационное поле. Изменяя параметры взаимодействия, можно создать аналог горизонта событий, отделяющего область, из которой ничто не может вырваться, от остальной Вселенной. Такой подход позволяет изучать квантовые эффекты в сильных гравитационных полях в контролируемых лабораторных условиях, недоступных при прямом исследовании астрофизических чёрных дыр. Ключевым преимуществом является возможность наблюдения за эволюцией квантовых состояний и их взаимодействием с аналогом горизонта событий.
Для точного моделирования гравитационных сил вблизи чёрной дыры, в спиновой цепи используется зависимое от позиции взаимодействие между узлами. Вместо однородного взаимодействия, сила связи между соседними спинами изменяется в соответствии с предполагаемой метрикой искривлённого пространства-времени. Более сильное взаимодействие моделирует большую гравитационную силу, а более слабое — меньшую. Такой подход позволяет создать аналоговую модель гравитационного поля, в которой изменение силы взаимодействия вдоль цепи воспроизводит градиент гравитационного потенциала вблизи чёрной дыры, что необходимо для изучения эффектов, связанных с горизонтом событий и искривлением пространства-времени.
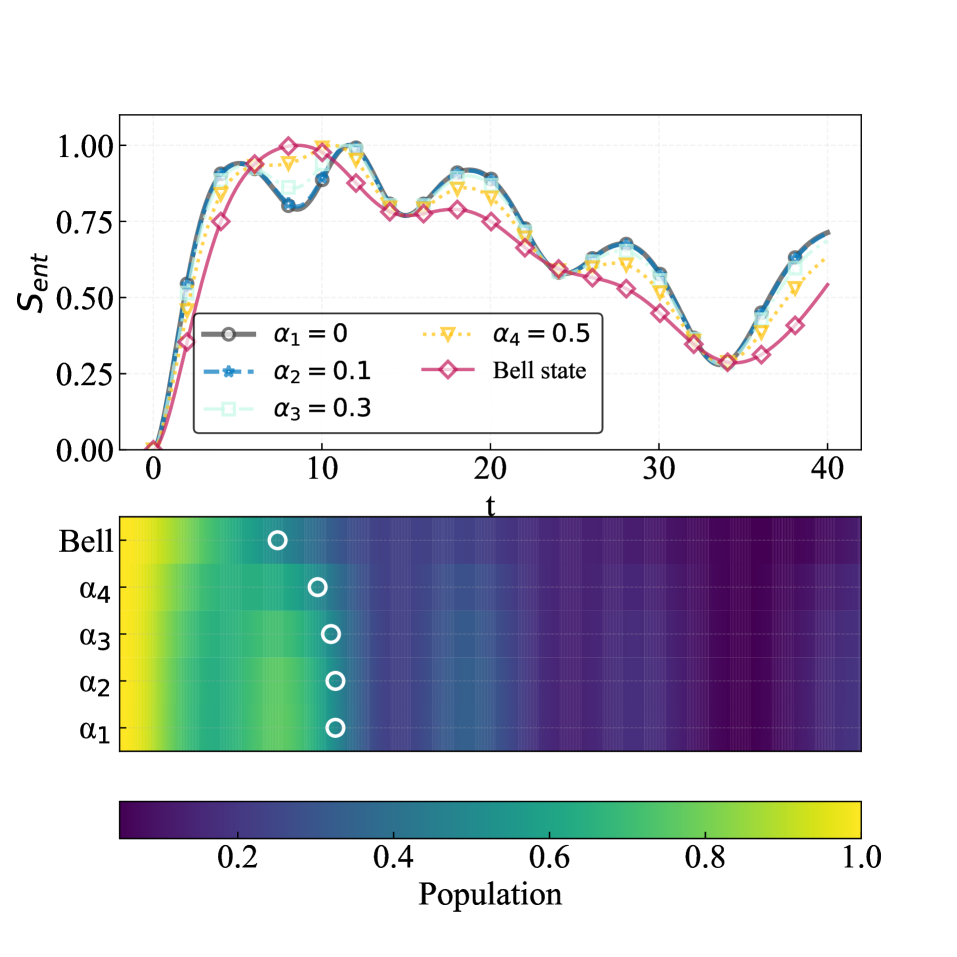
Исследователи используют энтропию запутанности в спиновой цепи для количественной оценки передачи информации и изучения поведения излучения Хокинга. Измерение энтропии запутанности между различными участками цепи позволяет определить степень корреляции между ними, что служит индикатором передачи информации. В контексте аналогии с черной дырой, увеличение энтропии запутанности при приближении к горизонту событий соответствует увеличению количества информации, которая становится недоступной для внешнего наблюдателя. Анализ зависимости энтропии запутанности от различных параметров спиновой цепи позволяет моделировать процессы, происходящие при испарении черной дыры и проверять теоретические предсказания относительно сохранения информации, в частности, парадокс информационного исчезновения.
Модель спиновой цепи позволяет проводить контролируемые исследования квантовой когерентности и её роли в сохранении информации при испарении чёрной дыры. В частности, анализируя динамику запутанности в системе, исследователи могут моделировать процессы, происходящие вблизи горизонта событий, и изучать, как квантовые корреляции влияют на сохранение информации, которая, казалось бы, теряется при испарении. Такой подход позволяет проверять гипотезы о разрешении информационного парадокса чёрных дыр и оценивать эффективность механизмов, предотвращающих полную потерю квантовой информации во время процесса испарения \hbar . Контролируемый характер модели позволяет исключить внешние факторы и сосредоточиться исключительно на квантовых эффектах, связанных с когерентностью и запутанностью.
Измерение и Интерпретация Квантовой Когерентности
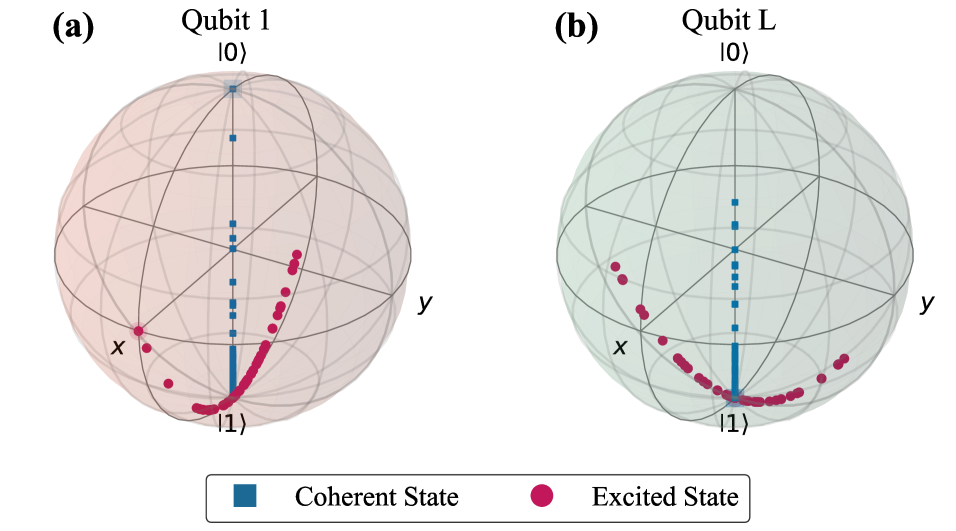
Для количественной оценки квантовой когерентности, то есть способности квантовых состояний сохранять фазовые соотношения в процессе имитации испарения, используется L1-норма. Этот показатель позволяет точно определить, насколько сильно квантовые состояния подвержены декогеренции — потере квантовой информации. В ходе исследований, L1-норма применяется для отслеживания эволюции квантовых состояний, выявляя моменты, когда фазовые соотношения начинают разрушаться, что напрямую указывает на степень потери когерентности. Более низкое значение L1-нормы свидетельствует о сохранении когерентности и, следовательно, о потенциальной возможности восстановления информации, закодированной в квантовых корреляциях, в то время как её увеличение указывает на прогрессирующее разрушение квантовой информации и потерю когерентности.
Анализ кривой Пейджа, описывающей эволюцию энтропии запутанности, подтверждает теоретические предсказания о сохранении информации в процессе испарения черной дыры. Ключевым моментом является так называемое “время Пейджа” — момент времени, когда примерно половина первоначальных возбуждений покидает систему. Именно в этот период наблюдается начало восстановления информации, ранее казавшейся потерянной. Данный результат демонстрирует, что информация не уничтожается, а перераспределяется и кодируется в тонких квантовых корреляциях между излучением Хокинга и остатком черной дыры, что согласуется с принципом унитарности в квантовой механике. Полученные данные позволяют более глубоко понять природу черных дыр и механизмы сохранения информации в экстремальных гравитационных условиях.
Исследователи применяют энтропию фон Неймана для точного измерения степени запутанности между различными сегментами спиновой цепи, что позволяет получить ценные сведения о содержании информации в излучении Хокинга. Этот метод позволяет количественно оценить корреляции между частицами, даже когда они разделены горизонтом событий, и выявить, как информация, первоначально заключенная в черной дыре, постепенно высвобождается в процессе испарения. S = -Tr(\rho \log \rho) — формула, определяющая энтропию фон Неймана, где ρ — матрица плотности, описывающая состояние системы. Точное определение запутанности с помощью данной величины позволяет проверить, действительно ли информация не теряется, а лишь кодируется в тонких квантовых корреляциях, доступных для анализа в излучении Хокинга, что является ключевым моментом в разрешении информационного парадокса.
Исследования, использующие такие инструменты как норма L1, энтропия фон Неймана и анализ кривой Пейджа, предоставляют возможность проверить гипотезу о том, что информация, казалось бы, исчезающая в черных дырах, на самом деле не утрачивается. Вместо этого, данные свидетельствуют о том, что информация кодируется в тонких квантовых корреляциях, проявляющихся в излучении Хокинга. Ученые смогли измерить и интерпретировать квантовую когерентность, показывая, что фазовые соотношения между квантовыми состояниями сохраняются даже в процессе «испарения» черной дыры. Подобный подход позволяет отследить эволюцию запутанности и определить момент, когда примерно половина начальных возбуждений покидает систему — так называемое «время Пейджа», которое коррелирует с началом восстановления информации, подтверждая, что информация не уничтожается, а переносится в коррелированные квантовые состояния.
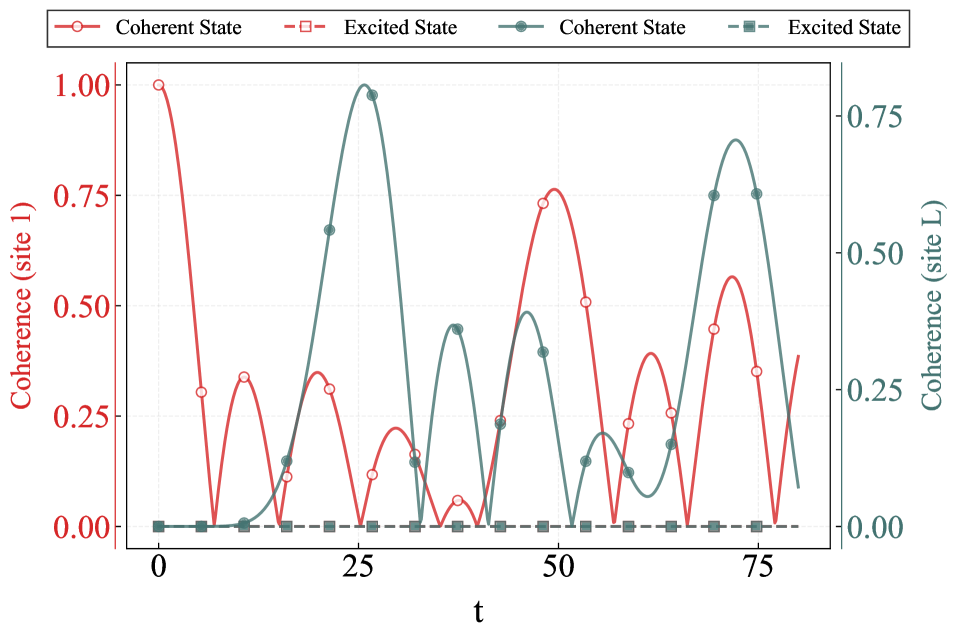
Исследование, посвященное эмуляции горизонта событий черной дыры с помощью спиновой цепи XY, закономерно подтверждает, что даже элегантные теоретические конструкции сталкиваются с суровой реальностью реализации. Попытки удержать квантовую информацию, продемонстрированные в работе, напоминают тщетные усилия удержать песок сквозь пальцы. Как метко заметил Карл Поппер: «Нельзя доказать, что что-либо является истинным, но можно доказать, что оно ложно». В контексте данной работы, это означает, что, хотя полная демонстрация кривой Пейджа остается недостижимой, обнаружение переноса квантовой информации и когерентности служит мощным опровержением наивных представлений об исчезновении информации в черных дырах. Похоже, каждая «революционная» технология завтра станет техдолгом, поскольку практическая реализация всегда добавляет новые слои абстракции и компромиссов.
Что дальше?
Наблюдаемая в данной работе имитация кривой Пейджа, реализованная на базе XY спиновой цепи, не является, разумеется, окончательным ответом на парадокс информации чёрных дыр. Скорее, это очередной элегантный способ убедиться в том, что энтропия — дама капризная, и её подсчёт всегда будет представлять собой проблему. Всё это, конечно, любопытно, но следует помнить, что аналоговые модели гравитации — это всё-таки лишь аналогии. В реальной чёрной дыре всё будет сложнее — и, вероятно, менее изящно.
Более того, сохранение когерентности, продемонстрированное в эксперименте, остаётся узким местом. В реальных астрофизических сценариях, с учётом взаимодействия с окружением, когерентность, вероятно, исчезнет быстрее, чем успеет сформироваться кривая Пейджа. Поэтому, следующие шаги неизбежно связаны с поиском механизмов защиты когерентности или, что более вероятно, с разработкой моделей, в которых её потеря не является фатальной.
В конечном счёте, вся эта работа — лишь ещё один кирпичик в огромной стене, отделяющей нас от понимания фундаментальных законов Вселенной. И, как показывает опыт, каждый новый кирпичик требует всё больше усилий для установки, а стена всё равно не становится выше.
Оригинал статьи: https://arxiv.org/pdf/2602.07043.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Прогнозы криптовалюты AXS: информация о ценах на AXS
- Откровенные заметки, слитые стримером Lacari, привели к его бану на Twitch и Kick.
- Решение головоломки с паролем Absolum в Yeldrim.
- Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip
- Нечестивцам нет покоя: как получить старый ключ от коттеджа
- Все рецепты культистского круга в Escape from Tarkov
- Кто такая Кселия Мендес-Джонс? 5 вещей, которые нужно знать об актере Fallout
- Arknights: Endfield — Интерактивная карта (Долина IV)
- Акции UGLD. Южуралзолото ГК: прогноз акций.
- YAPYAP Список заклинаний
2026-02-10 16:26