Квантовая Механика за Пределами Гильбертова Пространства

Автор: Денис Аветисян

В статье рассматривается подход к завершению квантовой механики, включающий стохастическую динамику и явное представление траекторий частиц.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал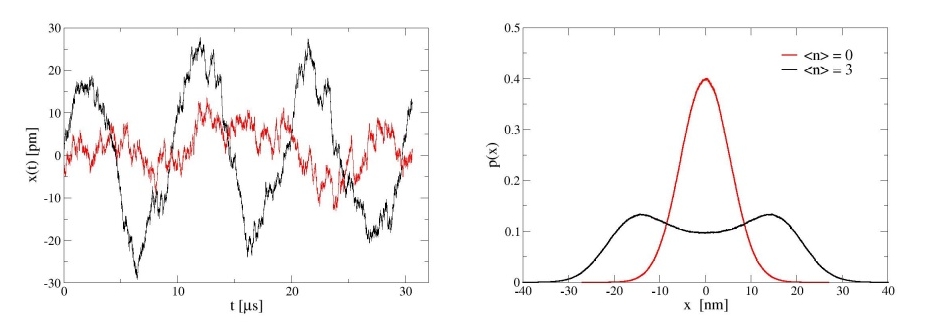

Наблюдения за эволюцией основного состояния и когерентного состояния с энергией $3\hbar\omega$ в классическом движении демонстрируют различия в вероятностных распределениях положения частицы, указывая на фундаментальные отличия в динамике этих квантовых состояний.

Квантовая аналитическая механика с использованием скрытых переменных как решение проблемы измерения.

Вопрос о полноте квантовой механики и возможности существования скрытых переменных остаётся одним из ключевых в современной физике. В данной работе, ‘Quantum Analytical Mechanics: Quantum Mechanics with Hidden Variables’, предлагается расширение стандартного квантовомеханического формализма посредством введения стохастических траекторий в конфигурационном пространстве системы. Такой подход позволяет описать процесс измерения как динамический физический процесс, непосредственно взаимодействующий с наблюдаемыми переменными, и, тем самым, обогатить инструментарий для анализа квантовых явлений. Способно ли данное развитие разрешить проблему измерения и предоставить более полное физическое описание квантового мира?

За пределами гильбертова пространства: к динамическому описанию квантового мира

Стандартная квантовая механика, основанная на гильбертовом пространстве, несмотря на свои впечатляющие успехи в предсказании результатов экспериментов, предоставляет по большей части статичную картину квантовых систем. В рамках этого подхода, частица описывается волновой функцией, определяющей вероятность её нахождения в определенной точке пространства, но отсутствует явное описание траектории её движения или динамической эволюции во времени, кроме как через решение $Шрёдингера$ уравнения. Данное ограничение не позволяет полноценно моделировать сложные квантовые явления, особенно процессы измерения и поведение частиц, находящихся в неравновесном состоянии. Хотя $Шрёдингерово$ уравнение определяет изменение волновой функции во времени, оно не дает представления о конкретном пути, который проходит частица, а лишь описывает эволюцию вероятностей. Таким образом, стандартный формализм, в большей степени ориентирован на статистическое описание, чем на динамическую картину движения отдельных частиц.

Статическое описание квантовых систем, присущее стандартной механике Гильберта, создает значительные трудности при моделировании сложных квантовых явлений. В частности, процесс измерения, который является фундаментальным для квантовой механики, плохо описывается в рамках этого подхода, поскольку предполагает мгновенное «коллапсирование» волновой функции. Кроме того, поведение частиц, находящихся в неравновесных состояниях — например, в условиях сильных взаимодействий или быстро меняющихся внешних воздействий — требует более динамичного подхода, способного учесть эволюцию системы во времени. Неспособность адекватно описать эти явления указывает на необходимость разработки квантовой теории, которая не только предсказывает вероятности различных исходов, но и позволяет проследить траектории отдельных частиц, согласующиеся как с теоретическими предсказаниями, так и с экспериментальными данными.

Необходимость динамически полной квантовой теории обусловлена ограничениями стандартного формализма, описывающего лишь статические состояния систем. Исследования показывают, что анализ индивидуальных траекторий частиц позволяет разрешить проблему измерения, традиционно вызывающую сложности в интерпретации квантовой механики. Вместо вероятностного описания, динамический подход позволяет проследить эволюцию каждой частицы во времени, согласуясь как с теоретическими предсказаниями, так и с экспериментальными данными. Такой метод предполагает, что частица имеет определенную траекторию, даже в процессе измерения, что позволяет избежать противоречий, возникающих при рассмотрении суперпозиции состояний. В результате, динамическое описание не только расширяет возможности моделирования сложных квантовых явлений, но и предоставляет более интуитивно понятную картину квантового мира, позволяя преодолеть некоторые фундаментальные трудности современной физики.

Механика Нельсона: фундамент для квантовой динамики

Механика Нельсона представляет собой ньютоноподобный подход к описанию квантовых систем, рассматривая частицы как объекты, подверженные диффузионным процессам. В основе этого подхода лежит стохастическое дифференциальное уравнение, определяющее траектории частиц во времени. В отличие от детерминированной механики, где траектория однозначно определяется начальными условиями, в механике Нельсона траектория носит случайный характер, описываемый вероятностным распределением. Это уравнение имеет вид $dX_t = \sqrt{2S(X_t, t)} dW_t + V(X_t, t)dt$, где $X_t$ — положение частицы в момент времени $t$, $S(X_t, t)$ — квантовый потенциал, $V(X_t, t)$ — обычное потенциальное поле, а $dW_t$ — винеровский процесс, определяющий случайную составляющую движения.

Механика Нельсона, рассматривающая квантовые системы как диффузионные процессы, обеспечивает естественное описание траекторий частиц и предлагает подход к разрешению проблемы измерения. В рамках данной модели, частица движется по случайной траектории, определяемой стохастическим дифференциальным уравнением, что позволяет избежать недетерминированности, присущей стандартной квантовой механике. Это позволяет рассматривать процесс измерения не как внезапное «коллапсирование» волновой функции, а как естественное следствие диффузии, где вероятность обнаружения частицы в определенной точке определяется плотностью вероятности, эволюционирующей согласно уравнению, аналогичному уравнению диффузии. Таким образом, проблема измерения в механике Нельсона сводится к задаче описания эволюции этой плотности вероятности, что устраняет необходимость в постулате о коллапсе волновой функции и предлагает детерминистическую интерпретацию квантовых явлений.

Уравнения Маделунга устанавливают прямую связь между стохастической механикой Нельсона и уравнением Шрёдингера, представляя собой мост между классическим и квантовым описанием. Эти уравнения, полученные преобразованием уравнения Шрёдингера, выражают квантовую волновую функцию $\Psi$ через скалярное поле, описывающее плотность вероятности, и векторное поле, описывающее скорость частицы. В частности, уравнение непрерывности, являющееся частью уравнений Маделунга, гарантирует сохранение вероятности, а уравнение импульса связывает эволюцию волновой функции с градиентом потенциала и скоростью частицы. Это позволяет интерпретировать квантовую механику как диффузионный процесс, в котором частицы движутся под влиянием потенциала и случайных сил, что обеспечивает классическое описание траекторий частиц в рамках квантовой теории.

Квантовая аналитическая механика: расширение стохастической основы

Квантовая аналитическая механика расширяет стохастическую механику Нельсона, предоставляя основу для моделирования сложных квантовых систем и процессов. В частности, она позволяет детально исследовать эксперимент Штерна-Герлаха, описывая эволюцию спина частиц во внешнем магнитном поле, и анализировать поведение частиц в конфигурационном пространстве, учитывая вероятностную природу их траекторий. Данный подход позволяет моделировать системы, где классическое описание не применимо, и предоставляет инструменты для изучения корреляций между частицами, а также их динамики во времени и пространстве, обеспечивая более полное представление о квантовых явлениях.

Квантовая аналитическая механика использует стохастические процессы для описания динамики частиц, позволяя проводить детальный анализ квантовых траекторий и корреляций. В экспериментах по левитации достигнуто временное разрешение в 32 нс, что позволяет отслеживать изменения в положении и импульсе частиц с высокой точностью. Данный подход позволяет моделировать движение частиц, учитывая случайные флуктуации, и выявлять статистические закономерности в их поведении, предоставляя более полное представление о квантовых процессах, чем классические детерминированные модели. Анализ траекторий позволяет вычислять различные корреляционные функции, характеризующие взаимодействие между частицами и их зависимость от внешних воздействий.

Квантово-аналитическая механика, используя формализм картины Боппа-Хаага, предоставляет возможность динамического моделирования вращающихся заряженных частиц и их магнитных моментов. Данный подход позволяет описывать частицы как объекты, обладающие внутренними степенями свободы, влияющими на их траектории и взаимодействия. В ходе первичного анализа пучка частиц, экспериментально было установлено, что ширина распределения частиц составляет 150 μм, что подтверждает возможность детального описания их динамического поведения и внутренних характеристик в рамках данной модели. Использование картины Боппа-Хаага обеспечивает корректное описание спиновых свойств частиц и их взаимодействие с внешними полями, что является ключевым для анализа сложных квантовых систем.

Эксперимент Штерна-Герлаха демонстрирует разделение пучков частиц с внутренним магнитным моментом, что воспроизводит оригинальную установку и позволяет наблюдать отклонение частиц в магнитном поле на расстоянии 9 см от начала.

Влияние и вызовы для теорий скрытых параметров

Квантовая аналитическая механика, развивая идеи теорий скрытых параметров, предлагает подход к разрешению проблемы нелокальности, выявленной теоремой Белла. В отличие от классических представлений, она постулирует существование дополнительных, скрытых переменных, определяющих поведение квантовых частиц и, таким образом, объясняющих кажущиеся парадоксальными корреляции между удалёнными частицами. Однако, даже при принятии концепции скрытых переменных, квантовая аналитическая механика сталкивается с необходимостью объяснения и согласования с экспериментальными данными, подтверждающими квантовую запутанность. Несмотря на то, что она потенциально способна обойти ограничения, накладываемые теоремой Белла, полное решение проблемы нелокальности требует дальнейшего исследования и уточнения, а также учета всех известных следствий квантовой механики, включая, например, нарушение неравенств Белла, наблюдаемое в многочисленных экспериментах.

Механика Бома представляет собой альтернативный подход к теориям скрытых параметров, функционирующий в рамках квантовой аналитической механики. В отличие от стандартной квантовой механики, которая описывает мир вероятностно, механика Бома постулирует существование скрытых переменных — точных положений частиц — которые определяют результаты измерений. Эти переменные не являются случайными, а детерминированно определяют результаты измерений, хотя и остаются недоступными для непосредственного наблюдения. В рамках этой теории, волновая функция играет роль «волнового пилота», направляющего частицы, что позволяет избежать нелокальности, постулируемой теоремой Белла, хотя и требует введения нетривиальной динамики. Таким образом, механика Бома предлагает детерминистическую интерпретацию квантовой реальности, сохраняя при этом предсказательную силу квантовой теории и открывая возможности для более глубокого понимания квантовых корреляций и запутанности.

Предлагаемый аналитический подход к квантовой механике, расширяющий концепцию скрытых переменных, открывает новые возможности для углубленного изучения квантовых корреляций и запутанности. Исследования в рамках данной структуры позволяют более детально рассмотреть взаимосвязи между удаленными частицами, выходя за рамки классического понимания локальности. Изучение запутанности, как фундаментального явления, позволяет приблизиться к пониманию истинной природы квантовой реальности, исследуя, каким образом информация может передаваться и сохраняться на квантовом уровне, и как это отличается от классических представлений о пространстве и времени. Анализ корреляций между частицами предоставляет инструменты для проверки различных теоретических моделей и поиска ответов на вопросы о природе квантового измерения и роли наблюдателя, что, в конечном итоге, способствует более полному пониманию основ квантовой механики и её связи с реальностью.

Перспективы: моделирование сложных квантовых систем

Квантовая аналитическая механика представляет собой перспективный подход к моделированию сложных квантовых систем, в частности, квантового гармонического осциллятора. В её основе лежит использование когерентных состояний — специальных волновых функций, позволяющих эффективно описывать поведение частиц и их динамику. В отличие от традиционных методов, данный подход позволяет упростить расчеты и получить аналитические решения для систем, которые ранее представляли значительные трудности. Использование когерентных состояний особенно полезно при изучении систем с большим числом частиц, где традиционные методы становятся вычислительно неподъемными. Такой подход открывает новые возможности для понимания и прогнозирования поведения квантовых систем, что имеет важное значение для развития передовых технологий, включая квантовые вычисления и сенсоры, а также создание новых материалов с уникальными квантовыми свойствами. Например, описание гармонического осциллятора через когерентные состояния позволяет аналитически рассчитать его энергетические уровни и волновые функции, что является ключевым шагом в понимании его физических свойств.

Перспективные возможности, открываемые данным подходом, простираются на широкий спектр передовых технологий. В области квантовых вычислений, точное моделирование сложных систем с использованием когерентных состояний может способствовать созданию более стабильных и эффективных кубитов. В сфере квантового зондирования, усовершенствованные модели позволяют проектировать датчики с беспрецедентной чувствительностью, способные обнаруживать мельчайшие изменения в окружающей среде. Кроме того, развитие новых квантовых материалов, обладающих уникальными свойствами, становится возможным благодаря более глубокому пониманию квантового поведения частиц в сложных структурах, что открывает перспективы для создания революционных устройств и технологий, например, сверхпроводников нового поколения или материалов с топологическими свойствами.

Дальнейшие исследования динамически полных квантовых теорий представляются критически важными для реализации всего потенциала квантовых технологий и углубления понимания квантового мира. Такие теории, в отличие от неполных, способны адекватно описывать эволюцию любой квантовой системы, предоставляя надежную основу для разработки новых квантовых устройств и материалов. Особое внимание уделяется поиску теорий, позволяющих эффективно моделировать сложные многочастичные системы, где традиционные подходы оказываются неэффективными. Прогресс в этой области обещает революционные изменения в областях квантовых вычислений, сенсорики и материаловедения, открывая возможности для создания принципиально новых технологий, основанных на уникальных свойствах квантовой механики, например, сверхбыстрых вычислений или высокочувствительных датчиков. Углубленное изучение динамической полноты позволит создавать более точные и надежные модели квантовых систем, что, в свою очередь, ускорит разработку и внедрение квантовых технологий в различные сферы жизни.

Исследование, представленное в данной работе, стремится к расширению стандартного формализма квантовой механики, вводя стохастическую динамику и явное представление траекторий частиц. Этот подход, направленный на решение проблемы измерения, предполагает, что полное описание физической реальности требует выхода за пределы гильбертова пространства. Как однажды заметил Пол Дирак: «Я не думаю, что физика должна быть понятной». Эта фраза отражает суть стремления к более глубокому, хотя и возможно, менее интуитивному пониманию квантового мира, где истина требует отхода от привычных представлений и готовности к принятию сложных, не всегда очевидных решений. В данном контексте, акцент на стохастических траекториях представляет собой попытку выйти за рамки вероятностного описания и приблизиться к детерминированному, но не обязательно предсказуемому, пониманию квантовых явлений.

Куда же дальше?

Представленные построения, несомненно, добавляют ещё один слой сложности к и без того непростой картине квантового мира. Вместо того чтобы окончательно ‘решить’ проблему измерения, они, скорее, переносят её в область определения начальных условий для стохастических траекторий. В этом нет ничего предосудительного — любая модель есть компромисс между знанием и удобством. Однако, возникает вопрос: оптимально ли это для кого? Вполне возможно, что стремление к ‘реальным’ траекториям лишь уводит от более глубокого понимания природы вероятности в квантовой механике.

Очевидным направлением дальнейших исследований является разработка вычислительно эффективных методов моделирования этих траекторий, особенно в контексте сложных многочастичных систем. Но более принципиальным представляется вопрос о связи между стохастической механикой Нельсона и другими подходами к интерпретации квантовой механики, такими как многомировая интерпретация Эверетта. Необходимо понять, являются ли эти подходы эквивалентными, или же они описывают различные аспекты одной и той же реальности.

В конечном итоге, истинное значение предложенных построений будет определяться не их математической элегантностью, а способностью предсказывать новые физические явления или разрешать давние экспериментальные парадоксы. Пока же, это — ещё один шаг на пути к пониманию, или, возможно, лишь иллюзия прогресса в бесконечном лабиринте квантовой реальности.

Оригинал статьи: https://arxiv.org/pdf/2511.21435.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2025-11-27 15:26