Квантовая Спутанность: От Комптоновского Рассеяния до Лимонада

Автор: Денис Аветисян

Новый подход к обнаружению квантовой запутанности использует вращательно-ковариантные измерения и показывает, что даже обыденные предметы, вроде стакана лимонада, могут выступать в роли эффективных детекторов.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал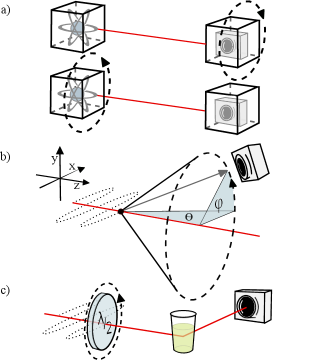

Изменение системы подготовки или детектора эквивалентно при описании ковариантных вращательно измерений, что демонстрируется на примере рассеяния фотонов поляризованными электронами под углами $\theta$ и $\varphi$, а также подтверждается экспериментом с лимонадом, где вращение поляризации фотонов полуволновой пластиной не влияет на детектирование при фиксированном угле.

Исследование предлагает фреймворк для обнаружения запутанности с использованием вращательно-ковариантных измерений, демонстрируя возможность применения простых систем, таких как стакан лимонада, для проведения квантовых экспериментов.

Обнаружение квантовой запутанности остается сложной задачей, требующей разработки эффективных и надежных методов. В работе «Entanglement Detection with Rotationally Covariant Measurements — From Compton Scattering to Lemonade» предложен новый подход, основанный на измерениях, ковариантных относительно вращений, позволяющий классифицировать такие системы всего одним параметром. Показано, что даже простые оптические системы, включая рассеяние света в напитках, могут служить детекторами запутанности, а предложенная методика сертификации запутанности обеспечивает точные границы даже в полу-устройство-независимых сценариях. Не откроет ли это путь к созданию доступных и инновационных квантовых экспериментов, используя неожиданные ресурсы, вроде стакана лимонада?

Квантовая Запутанность: За Пределами Классической Корреляции

Классическая физика сталкивается с фундаментальными трудностями при объяснении корреляций между частицами, которые превосходят любые ограничения, предсказываемые локальными теориями скрытых параметров. Эти теории предполагают, что кажущаяся случайность квантовых явлений на самом деле обусловлена неизвестными локальными переменными, определяющими поведение частиц. Однако, экспериментальные результаты неоднократно демонстрируют, что некоторые корреляции между частицами настолько сильны, что их невозможно объяснить, предполагая существование лишь локальных, предопределенных свойств. Такие корреляции предполагают нелокальную связь между частицами, то есть мгновенное влияние одной частицы на другую, независимо от расстояния между ними, что противоречит принципам классической физики и требует пересмотра представлений о природе реальности. Данное несоответствие является ключевым свидетельством в пользу квантовой механики и ее неклассического характера.

Явление квантовой запутанности, кажущееся парадоксальным с точки зрения классической физики, является фундаментальной основой квантовой информатики. В основе этого лежит корреляция между двумя или более частицами, которая сохраняется независимо от расстояния между ними. Эта связь, более сильная, чем любая, допустимая в рамках классических представлений о локальных скрытых переменных, позволяет создавать принципиально новые технологии. Запутанность используется в квантовой криптографии для обеспечения абсолютно безопасной передачи данных, в квантовых вычислениях — для создания кубитов и выполнения операций, недоступных классическим компьютерам, и в квантовой телепортации — для передачи квантового состояния на расстояние. Таким образом, исследование и практическое применение квантовой запутанности открывает новые горизонты в области информации и вычислений, представляя собой ключевой элемент будущего технологического прогресса.

Подтверждение истинной квантовой запутанности представляет собой сложную экспериментальную задачу, требующую исключения всех возможных классических объяснений наблюдаемых корреляций. Ученым необходимо тщательно разработать эксперименты и протоколы, чтобы убедиться, что полученные результаты нельзя объяснить скрытыми локальными переменными, которые могли бы имитировать квантовое поведение. Это предполагает точный контроль над экспериментальными условиями, эффективное обнаружение частиц и статистический анализ данных, позволяющий исключить любые лазейки, которые могли бы позволить классической теории сохранить правдоподобие. Доказательство нарушения неравенств Белла, основанных на классических предположениях, является одним из ключевых подходов, но даже в этом случае необходима тщательная проверка экспериментальной установки на предмет потенциальных систематических ошибок и уязвимостей, гарантирующих, что наблюдаемые корреляции действительно имеют квантовую природу и не являются результатом незамеченных классических факторов.

Анализ минимальных значений негативности, полученных путем решения SDP (7) с использованием решателя MOSEK в CVXPY для неизвестных образцов устройств, показывает, что запутанность обнаруживается для устройств с rArB≥0.4, при условии rA=rB.

Описание Квантового Состояния: Инструменты для Обнаружения

Квантовые состояния, особенно проявляющие запутанность, математически описываются с помощью операторов плотности. В отличие от векторов состояния, которые описывают чистые состояния, операторы плотности позволяют описывать также смешанные состояния и статистические ансамбли. Оператор плотности, обозначаемый как $\rho$, является самосопряженной, положительно полуопределенной матрицей с трассой, равной единице. Матрица плотности предоставляет полное описание состояния квантовой системы, включая вероятности нахождения системы в различных чистых состояниях. Это особенно важно при анализе экспериментальных данных, где реальные квантовые системы часто находятся в смешанных состояниях из-за взаимодействия с окружающей средой или несовершенства измерений. Использование операторов плотности позволяет корректно учитывать статистические свойства системы и проводить количественный анализ запутанности.

Операторы плотности, являясь матрицами, полностью описывают квантовое состояние системы, включая как чистые, так и смешанные состояния, и позволяют вычислить вероятности получения различных результатов измерений. В контексте экспериментов по обнаружению запутанности, операторы плотности используются для количественной оценки степени запутанности, например, посредством вычисления критериев запутанности, таких как критерий PPT (Positive Partial Transposition) или критериев, основанных на неравенствах Белла. Использование операторов плотности необходимо для корректной интерпретации экспериментальных данных, поскольку они позволяют учесть статистические ансамбли и несовершенства измерений, обеспечивая надежное подтверждение или опровержение наличия запутанности в исследуемой системе. Например, для бикубитной системы, оператор плотности $\rho$ является $4 \times 4$ матрицей, описывающей вероятности всех возможных состояний.

Учет симметрий системы, в частности, ковариантности относительно вращений, значительно упрощает описание квантовых состояний и процедур измерений. В квантовой механике, вращения являются фундаментальными преобразованиями, и использование симметрий позволяет перейти к более удобным системам координат и уменьшить количество независимых параметров, необходимых для полного описания состояния. Например, при описании состояний с вращательной симметрией, можно использовать угловые моменты и их проекции, что приводит к упрощению математического аппарата. Использование симметрий также позволяет предсказывать поведение системы при различных преобразованиях и существенно снижает вычислительную сложность при моделировании и анализе экспериментов, особенно в контексте обнаружения запутанности и других неклассических эффектов.

Обнаружение запутанности возможно для устройств с параметрами, удовлетворяющими условию rA⋅rB≥0,393, что подтверждается минимальной негативностью, полученной при решении SDP (7) для идеальных гипотетических устройств.

Выявление Запутанности: Экспериментальные Подходы

Для регистрации запутанности необходимы высокоточные измерения квантовых состояний, что обычно достигается с использованием схем детектирования запутанности. Эти схемы основаны на установлении неклассических корреляций между измеряемыми параметрами, например, поляризацией фотонов или спином частиц. Определение запутанности требует исключения возможности объяснения наблюдаемых корреляций локальными скрытыми переменными, что подтверждается нарушением неравенств Белла. Точность измерений критически важна, поскольку шум и погрешности могут маскировать истинные квантовые корреляции и привести к ложноотрицательным результатам. Статистический анализ данных, включающий расчет функций корреляции и коэффициентов видимости, необходим для подтверждения наличия запутанности и количественной оценки ее степени.

Для характеризации поляризованных фотонов и выявления запутанности в экспериментах может использоваться так называемый “Lemonade Detector” (лимонный детектор). Данный подход основан на использовании жидкой среды, в которой происходит взаимодействие фотонов с молекулами жидкости. Анализ изменений поляризации фотонов после прохождения через жидкость позволяет определить их корреляции и, следовательно, подтвердить наличие квантовой запутанности. В частности, наблюдается изменение в статистике рассеянных фотонов, которое невозможно объяснить классической физикой и служит доказательством неклассической корреляции между ними. Эффективность детектора зависит от оптических свойств используемой жидкости и точности измерения поляризации.

Эффект Комптона, заключающийся во взаимодействии фотонов с электронами, может быть использован для генерации и исследования запутанных состояний. В частности, при рассеянии фотонов на электронах сохраняется информация о поляризации, что позволяет создавать корреляции между рассеянными фотонами. Эти корреляции, при соответствующей настройке эксперимента, демонстрируют нарушение неравенств Белла, подтверждая наличие квантовой запутанности. Использование рассеяния Комптона позволяет исследовать запутанность в различных степенях свободы фотонов, включая поляризацию и импульс, и может быть реализовано с использованием различных источников излучения, включая синхротронное излучение и лазеры.

Два поляриметра Комптона регистрируют совпадения фотонов, рассеянных электронами из источника ортогонально линейно поляризованного (запутанного) излучения, в направлениях (θA, 0) и (θB, Δφ).

К Независимой Проверке: Новый Подход

Существенная проблема в обнаружении запутанности заключается в обеспечении надёжности измерительных приборов. Несовершенство аппаратуры может приводить к ложным результатам, имитирующим наличие запутанности там, где её на самом деле нет. Это связано с тем, что любое отклонение от идеальных измерений вносит систематические ошибки, которые могут быть интерпретированы как корреляции между частицами, даже если они независимы. Поэтому, для достоверного подтверждения запутанности необходимо тщательно учитывать и минимизировать влияние этих несовершенств, либо разрабатывать методы, устойчивые к аппаратным ошибкам. По сути, достоверность экспериментального подтверждения запутанности напрямую зависит от калибровки и точности используемого оборудования, что представляет собой значительный технический вызов.

Полу-независимость от устройств представляет собой перспективный подход к проверке запутанности, позволяющий минимизировать предположения о надежности измерительных приборов. Традиционно, подтверждение запутанности требовало точной калибровки и доверия к аппаратуре, что открывало возможность для фальсификации результатов за счет скрытых дефектов. Данный подход, напротив, позволяет выявлять запутанность, опираясь на более общие принципы, что существенно повышает надежность экспериментальных результатов. Он позволяет обнаружить корреляции, которые невозможно объяснить локальными реалистичными теориями, даже если измерительные приборы не идеальны, что открывает новые возможности для квантовых технологий и фундаментальных исследований.

Данное исследование представляет собой новую методологию обнаружения запутанности, основанную на ротационно ковариантных измерениях. Экспериментально достигнутый контраст детектора, равный 0.704 при использовании “яблочного лимонада”, превосходит теоретический предел для комптоновского рассеяния фотонов, возникающих при аннигиляции позитронов и электронов. Этот результат демонстрирует повышенную чувствительность и надежность в обнаружении квантовой запутанности, открывая перспективы для создания более устойчивых к ошибкам квантовых технологий и систем связи, поскольку минимизирует влияние несовершенства измерительных приборов на достоверность результатов.

Анализ распределения мощности показал коэффициент корреляции r = 0.704 ± 0.001 при расстоянии 15 мм, при этом основная неопределенность обусловлена стабильностью интенсивности лазера и описывается функцией f(φ) = a(1 + r cos(2(φ + φ₀))).

Исследование демонстрирует, что обнаружение запутанности не требует сложных установок. Авторы предлагают подход, основанный на ковариантных измерениях, показывая, что даже простая система, вроде стакана лимонада, может выступать в роли эффективного детектора. Это согласуется с идеей о том, что порядок возникает из локальных правил, а не нуждается в централизованном контроле. Как заметил Джон Белл: «Если вы не можете понять, как работает что-то, то простое описание будет лучше сложного». Эта простота подхода и является ключом к практическому применению квантовых явлений, позволяя обойти необходимость в сложных системах и сосредоточиться на фундаментальных принципах взаимодействия.

Что дальше?

Представленная работа, демонстрируя возможность обнаружения запутанности с помощью ковариантных измерений, поднимает вопрос не о проектировании детекторов, а об их неизбежном возникновении. Если даже стакан лимонада способен зафиксировать квантовую корреляцию, то граница между инструментом и средой становится размытой. Важно понимать: устойчивость обнаружения не заложена в сложность прибора, а проистекает из локальных правил взаимодействия, из фундаментальной симметрии, свойственной природе.

Очевидным направлением дальнейших исследований представляется отказ от попыток создания «идеальных» измерений. Вместо этого, целесообразно сосредоточиться на изучении влияния шума и несовершенства на устойчивость детектирования. Возможно, именно в этих «неточностях» кроется ключ к созданию действительно практических квантовых устройств, способных функционировать в реальных условиях, а не в вакууме теоретических моделей.

Понимание того, что глобальное поведение возникает из локальных взаимодействий, требует пересмотра подхода к квантовым экспериментам. Необходимо отказаться от представления о контроле и признать, что влияние — более реалистичная цель. Малые взаимодействия создают огромные сдвиги, и задача исследователя — не управлять этими сдвигами, а научиться их распознавать и использовать.

Оригинал статьи: https://arxiv.org/pdf/2512.03984.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2025-12-04 19:20