Квантовая запутанность гиперонов: эволюция и перераспределение

Автор: Денис Аветисян

Новое исследование показывает, как квантовая запутанность изменяется в процессе распада пар гиперон-антигиперон, открывая возможности для управления квантовыми корреляциями.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал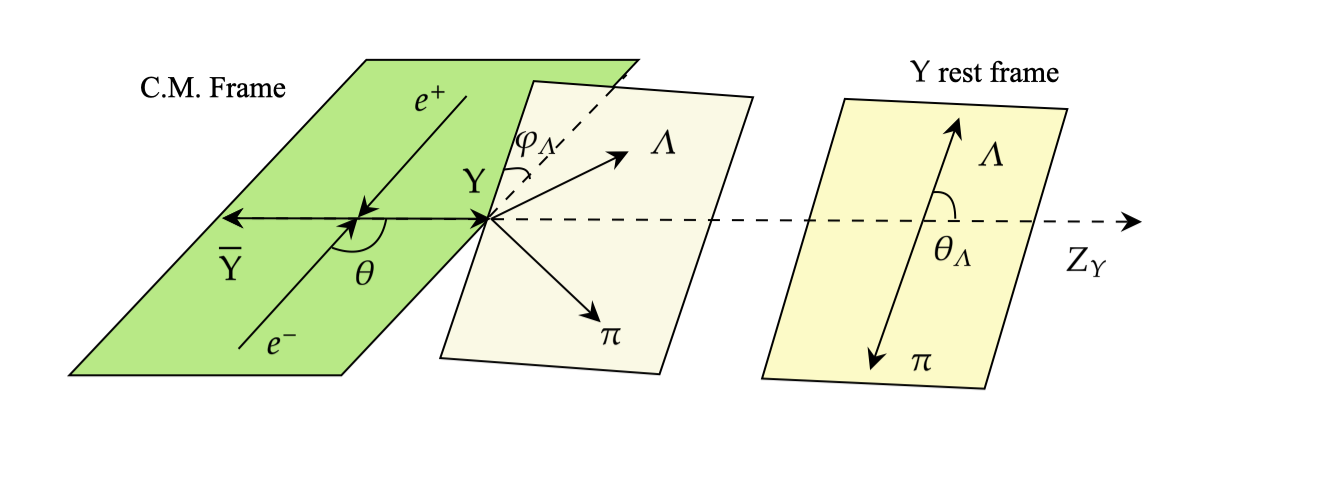

Определение углов гелицитности для распадов <span class="katex-eq" data-katex-display="false">e^{+}e^{-}\to Y\bar{Y}</span> и последовательного распада <span class="katex-eq" data-katex-display="false">Y\rightarrow\Lambda\pi</span> позволяет установить взаимосвязь между спиновыми состояниями частиц и кинематическими параметрами процесса, при этом аналогичные определения для <span class="katex-eq" data-katex-display="false">\bar{Y}\rightarrow\bar{\Lambda}\pi</span> опущены для краткости. — Определение углов гелицитности для распадов $e^{+}e^{-}\to Y\bar{Y}$ и последовательного распада $Y\rightarrow\Lambda\pi$ позволяет установить взаимосвязь между спиновыми состояниями частиц и кинематическими параметрами процесса, при этом аналогичные определения для $\bar{Y}\rightarrow\bar{\Lambda}\pi$ опущены для краткости.

В статье рассматривается эволюция квантовой запутанности в процессе последовательного распада пар гиперон-антигиперон с использованием матрицы плотности спина и показателей запутанности, таких как конуррентность и негативность.

helpНесмотря на фундаментальную роль запутанности в квантовой механике, ее поведение в каскадных процессах распада, таких как распад гиперонов, остается недостаточно изученным. Настоящая работа, озаглавленная ‘Entanglement redistribution of hyperon-antihyperon pair via sequential decay’, посвящена исследованию перераспределения квантовой запутанности в парах гиперон-антигиперон, образующихся при распаде. Показано, что запутанность может как усиливаться, так и ослабевать в процессе последовательных распадов, но не исчезает полностью, при этом важную роль играет поляризация гиперонов. Возможно ли, что подобные механизмы перераспределения запутанности являются универсальными для других процессов распада тяжелых частиц и могут найти применение в квантовых технологиях?

Квантовые корреляции: За пределами классического мира

Традиционные корреляции, широко используемые в науке и технике, оказываются недостаточными для полного описания квантовых систем. Хотя они и позволяют выявлять статистические связи между переменными, они не способны уловить всю сложность и нелокальность, присущие квантовому миру. Квантовые системы демонстрируют корреляции, которые не имеют классических аналогов, обусловленные такими явлениями, как суперпозиция и запутанность. Эти корреляции проявляются в виде более сильных и сложных связей между частицами, чем это возможно в классической физике, и позволяют им демонстрировать поведение, которое кажется невозможным с точки зрения нашего повседневного опыта. Таким образом, для полного понимания и эффективного использования возможностей квантовых систем требуется выход за рамки классических представлений о корреляциях и разработка новых методов анализа, способных уловить их уникальные особенности.

Квантовая механика вводит принципиально иные типы корреляций, не имеющие аналогов в классической физике. Эти корреляции возникают благодаря таким фундаментальным явлениям, как суперпозиция и запутанность. Суперпозиция позволяет квантовой системе одновременно находиться в нескольких состояниях, а запутанность создает связь между частицами, независимо от расстояния между ними. В результате, измерения над одной запутанной частицей мгновенно влияют на состояние другой, что невозможно в рамках классической картины мира. Эти квантовые корреляции не просто статистические связи, а отражают глубокую взаимосвязанность квантовых систем, открывая возможности для принципиально новых технологий, таких как квантовые вычисления и квантовая криптография. Изучение и понимание этих корреляций является ключевым шагом к раскрытию потенциала квантового мира.

Понимание квантовых корреляций имеет решающее значение для прогресса в области квантовых технологий и углубления фундаментальных знаний о природе реальности. В отличие от классических корреляций, которые описывают статистические зависимости между отдельными событиями, квантовые корреляции возникают из принципов суперпозиции и запутанности, позволяя частицам проявлять взаимосвязанное поведение, не имеющее аналогов в классической физике. Изучение этих уникальных связей открывает перспективы для создания принципиально новых технологий, таких как квантовые вычисления и квантовая криптография, а также способствует более глубокому пониманию основных законов, управляющих Вселенной. Игнорирование квантовых корреляций при моделировании и разработке квантовых систем неизбежно приводит к неполным и неточным результатам, ограничивая потенциал этих передовых технологий.

Данная работа посвящена детальной характеристике и количественной оценке уникальных корреляций, присущих квантовым системам, что позволяет выйти за рамки классических представлений. Исследователи разработали новые методы для измерения степени “квантовости” этих корреляций, используя ρ — матрицу плотности, описывающую состояние системы. Анализ показывает, что классические корреляции, основанные на общей информации, не способны в полной мере отразить сложность квантовых взаимодействий, особенно в случаях запутанности и суперпозиции. Разработанные инструменты позволяют не только выявлять эти квантовые особенности, но и оценивать их вклад в различные физические процессы, что имеет ключевое значение для прогресса в области квантовых вычислений, коммуникаций и сенсорики. Полученные результаты открывают путь к созданию более точных моделей квантовых систем и разработке новых квантовых технологий.

Анализ процесса <span class="katex-eq" data-katex-display="false">e^{+}e^{-} \to \psi(2S) \to \Xi^{-}(\to \Lambda \pi^{-}) \bar{\Xi}^{+}(\to \bar{\Lambda} \pi^{+})</span> и <span class="katex-eq" data-katex-display="false">e^{+}e^{-} \to \psi(2S) \to \Xi^{0}(\to \Lambda \pi^{0}) \bar{\Xi}^{0}(\to \bar{\Lambda} \pi^{0})</span> показывает совпадение показателей согласованности для пар <span class="katex-eq" data-katex-display="false"> \Xi^{-}\bar{\Xi}^{+}</span> и <span class="katex-eq" data-katex-display="false"> \Lambda\bar{\Lambda}</span>, подтверждая корреляцию между ними. — Анализ процесса $e^{+}e^{-} \to \psi(2S) \to \Xi^{-}(\to \Lambda \pi^{-}) \bar{\Xi}^{+}(\to \bar{\Lambda} \pi^{+})$ и $e^{+}e^{-} \to \psi(2S) \to \Xi^{0}(\to \Lambda \pi^{0}) \bar{\Xi}^{0}(\to \bar{\Lambda} \pi^{0})$ показывает совпадение показателей согласованности для пар $\Xi^{-}\bar{\Xi}^{+}$ и $\Lambda\bar{\Lambda}$ , подтверждая корреляцию между ними.

Матрица плотности и методы корреляционного анализа

Матрица плотности спина (МПС) является мощным математическим инструментом для описания квантового состояния системы, особенно в контексте систем со спином. В отличие от волновой функции, которая описывает чистое состояние, МПС позволяет описывать смешанные состояния, представляющие собой статистическую смесь чистых состояний. Матрица плотности ρ — это оператор, действующий в гильбертовом пространстве, и характеризуется свойствами положительной полуопределенности и следа, равного единице ( $Tr(\rho) = 1$ ). Элементы матрицы плотности содержат информацию о вероятностях различных спиновых состояний системы и их корреляциях. Использование МПС особенно полезно при анализе систем, подверженных декогеренции или взаимодействию с окружающей средой, поскольку позволяет учитывать статистический характер их состояния.

Для экспериментального исследования квантовых состояний используются методы, основанные на распадах частиц, такие как распад чармония ( $J/\psi$ ) и гиперонов. В процессе распада чармония, образующиеся пары пионов или лептонов позволяют реконструировать исходное квантовое состояние. Аналогично, изучение продуктов распада гиперонов, например, лямбда-частиц ( $\Lambda^0$ ), позволяет определить спиновые корреляции и другие квантовые свойства. Анализ угловых распределений продуктов распада предоставляет информацию о поляризации исходных частиц и, следовательно, о структуре волновой функции исследуемой системы. Выбор конкретного метода зависит от доступных энергий и характеристик частиц, а также от требуемой точности измерения.

Экспериментальные методы, такие как анализ распадов чарония и гиперонов, позволяют получать доступ к корреляциям между частицами, возникающим из квантовой запутанности. Анализ этих корреляций осуществляется посредством измерения совместного распределения вероятностей состояний частиц и сравнения с предсказаниями классической физики. Наличие корреляций, нарушающих неравенства Белла, является прямым свидетельством квантовой запутанности, подтверждающим нелокальную природу связи между частицами, даже на больших расстояниях. $\rho_{AB}$ — матрица плотности, описывающая совместное состояние двух запутанных частиц A и B, используется для количественной оценки этих корреляций.

Тесты Белла представляют собой ключевой этап валидации при исследовании квантовых корреляций. Они основаны на проверке неравенств Белла, которые являются математическими ограничениями, выполняющимися для любых локальных реалистичных теорий. Нарушение этих неравенств, экспериментально подтвержденное для запутанных систем, доказывает нелокальный характер квантовых корреляций, то есть корреляцию между частицами, которая не может быть объяснена передачей информации со скоростью, не превышающей скорость света. Экспериментальная реализация тестов Белла требует точного контроля над запутанными состояниями и эффективного измерения соответствующих наблюдаемых для коррелированных частиц. Результаты этих тестов подтверждают фундаментальные принципы квантовой механики и исключают возможность объяснения квантовых явлений с помощью классических локальных теорий.

Измерение запутанности: количественные показатели и их применение

Коэффициенты Конкуренции (Concurrence) и Негативности (Negativity) представляют собой надежные количественные показатели запутанности, позволяющие оценить степень квантовой корреляции между кубитами. Конкуренция, определяемая как $C = max(0, \sqrt{1 - Tr(\rho^2)})$ , варьируется от 0 для не запутанных состояний до 1 для максимально запутанных состояний. Негативность, рассчитываемая как сумма отрицательных собственных значений матрицы частичной транспозиции $\rho^{\Gamma}$ , является мерой запутанности, которая также равна нулю для разделяемых состояний. Оба показателя инвариантны к локальным унитарным преобразованиям и предоставляют возможность количественно оценить степень неклассической корреляции, присутствующей в квантовой системе, что критически важно для анализа и разработки квантовых технологий.

Энтропия фон Неймана является ключевым параметром при вычислении мер запутанности, поскольку она количественно определяет степень смешанности квантового состояния. Смешанное состояние описывает статистическую смесь чистых квантовых состояний, и $S = -Tr(\rho \log_2 \rho)$ определяет энтропию фон Неймана для матрицы плотности ρ, характеризующей смешанное состояние. Чем выше значение энтропии фон Неймана, тем более смешанным является состояние и тем меньше классической информации оно содержит. При расчете таких мер запутанности, как конкорренция и негативность, энтропия фон Неймана используется для определения степени смешанности подсистем, что позволяет точно оценить силу квантовой корреляции между ними. Таким образом, энтропия фон Неймана служит необходимым инструментом для количественной оценки и анализа запутанности в квантовых системах.

Квантовая дискордация представляет собой меру корреляций, способную выявлять взаимосвязи даже в состоянии разделенных (separable) систем, в отличие от традиционных мер запутанности, которые обнуляются при разделении. Это расширяет наше понимание квантовых связей, позволяя идентифицировать неклассические корреляции, которые не связаны с запутанностью. В то время как запутанность требует наличия сильных корреляций и не может существовать в разделенных состояниях, квантовая дискордация позволяет зафиксировать более слабые, но всё же значимые взаимосвязи между подсистемами, что важно для анализа квантовых систем, где запутанность может быть незначительной или отсутствовать.

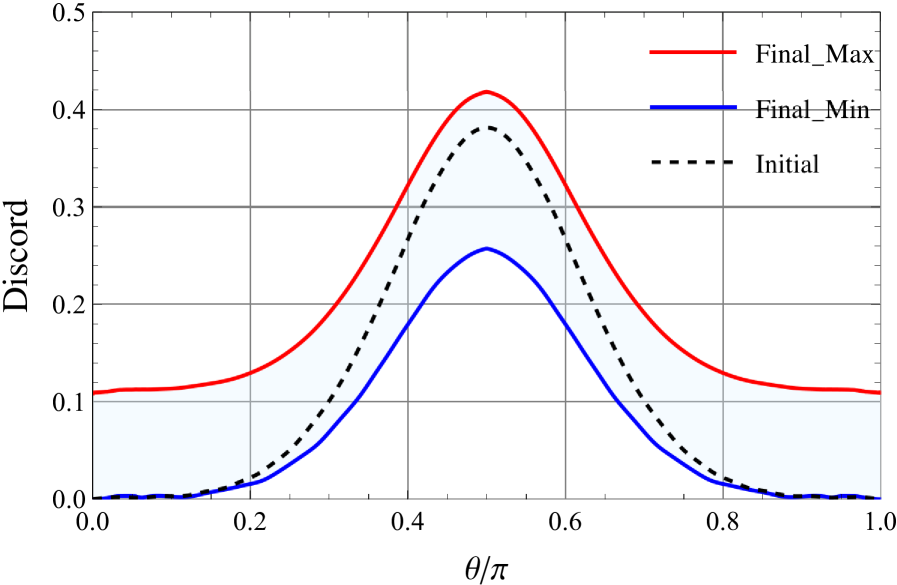
В ходе проведенного исследования установлено, что квантовая дискордация (quantum discord) демонстрирует устойчивое увеличение в процессе распадов гиперонов, даже в случаях, когда классические показатели запутанности (entanglement) остаются неизменными. Данный результат подчеркивает важность рассмотрения неклассических корреляций, выходящих за рамки просто запутанности, для более полного описания квантовых явлений. Наблюдаемое поведение указывает на то, что дискордация может служить индикатором квантовых корреляций, существующих даже в состояниях, которые не демонстрируют запутанность, что расширяет возможности анализа и понимания процессов в физике высоких энергий.

Наблюдения показали, что увеличение степени запутанности в процессе распада гиперонов зависит от параметров распада, в частности, от величины поперечной поляризации. Увеличение запутанности проявляется лишь при достаточно высокой поперечной поляризации распадающихся частиц. Количественно, значимое увеличение запутанности наблюдается только когда фазовый сдвиг $ΔΦ$ превышает 0.3 радиан. Это указывает на то, что для проявления и количественной оценки запутанности необходимо учитывать специфические кинематические характеристики процесса распада, а именно, параметры, определяющие поляризацию и фазовые соотношения между частицами.

В ходе анализа гиперонных распадов установлено, что увеличение степени запутанности наблюдается только при величине фазового сдвига (ΔΦ), превышающей 0.3 радиан. Данное условие является критическим для проявления эффекта увеличения запутанности; при значениях ΔΦ менее 0.3 радиан, значимых изменений в степени запутанности не регистрируется. Таким образом, фазовый сдвиг играет роль ключевого параметра, определяющего возможность наблюдения увеличения запутанности в рассматриваемых процессах распада. $\Delta\Phi$ является определяющим фактором, влияющим на наблюдаемый уровень квантовой корреляции.

Анализ корреляции и негативности в процессе <span class="katex-eq" data-katex-display="false">e^{+}e^{-}\to\psi(2S)\to\Xi^{-}(\to\Lambda\pi^{-})~\bar{\Xi}^{+}(\to\bar{\Lambda}\pi^{+})</span> показывает, что изменение <span class="katex-eq" data-katex-display="false">\Delta\Phi</span> на 0.3 радиана приводит к перекрытию кривых для <span class="katex-eq" data-katex-display="false">\Xi^{-}\bar{\Xi}^{+}</span> и <span class="katex-eq" data-katex-display="false">\Lambda\bar{\Lambda}</span>, в то время как при <span class="katex-eq" data-katex-display="false">\Delta\Phi = 0</span> наблюдается расхождение. — Анализ корреляции и негативности в процессе $e^{+}e^{-}\to\psi(2S)\to\Xi^{-}(\to\Lambda\pi^{-})~\bar{\Xi}^{+}(\to\bar{\Lambda}\pi^{+})$ показывает, что изменение $\Delta\Phi$ на 0.3 радиана приводит к перекрытию кривых для $\Xi^{-}\bar{\Xi}^{+}$ и $\Lambda\bar{\Lambda}$ , в то время как при $\Delta\Phi = 0$ наблюдается расхождение.

Устойчивость запутанности: автодистилляция и SLOCC

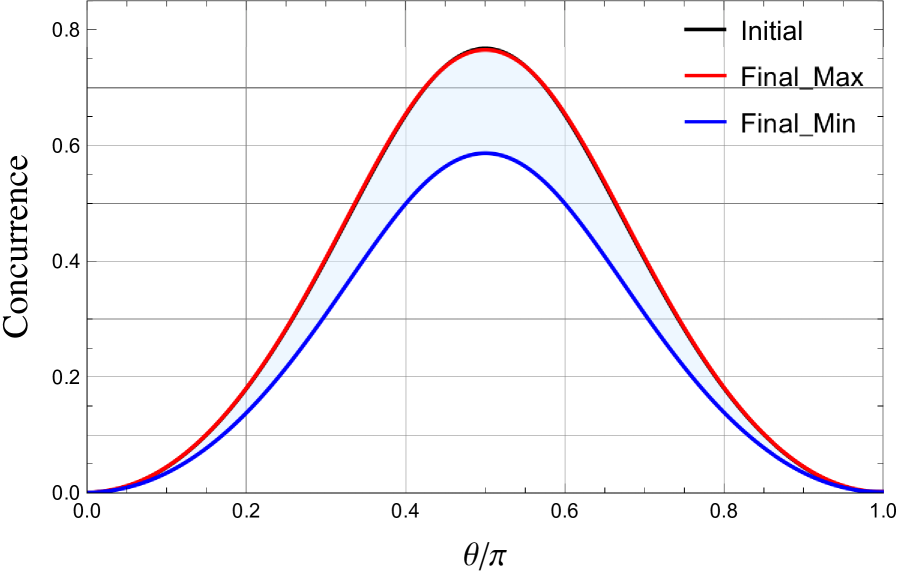
Исследования явления автодистилляции запутанности демонстрируют неожиданный эффект: в процессе распада частиц степень запутанности может не только сохраняться, но и возрастать. Этот процесс, кажущийся парадоксальным, обусловлен особенностями квантовой механики и позволяет выделять более чистые, сильно запутанные состояния из смешанных. В ходе распада, определенные корреляции между частицами могут усиливаться, приводя к увеличению $entanglement$ — меры неклассической связи. Данное явление имеет важное значение, поскольку указывает на то, что запутанность — это не хрупкий ресурс, разрушающийся при взаимодействии, а динамически поддерживаемое свойство, способное усиливаться даже в сложных квантовых системах, что открывает перспективы для повышения эффективности квантовых технологий.

Процесс трансформации запутанных состояний подчиняется строгим правилам, определяемым теорией Стохастических Локальных Операций и Классической Коммуникации (SLOCC). Данная теория устанавливает, какие операции допустимы над запутанными частицами без нарушения фундаментальных принципов квантовой механики. SLOCC описывает, как локальные измерения и классическая передача информации могут изменять запутанность, но при этом ограничивают возможные преобразования, предотвращая создание состояний, не соответствующих физическим законам. Именно благодаря этим ограничениям, предсказанным теорией SLOCC, возможно сохранение и даже увеличение запутанности в определенных процессах, таких как самодистилляция, что подчеркивает устойчивость квантовых корреляций и их потенциал как ценного ресурса для будущих квантовых технологий.

Наблюдаемое увеличение запутанности в процессе распада гиперонов указывает на удивительную устойчивость квантовых корреляций. Данное явление демонстрирует, что запутанность не является хрупким состоянием, легко разрушаемым внешними воздействиями, а напротив, способна усиливаться даже в условиях декогеренции. Это открытие имеет важное значение, поскольку подчеркивает потенциал запутанности как ценного ресурса для квантовых технологий. Увеличение степени запутанности позволяет предположить, что её можно эффективно использовать для повышения производительности квантовых вычислений, улучшения безопасности квантовой связи и создания более чувствительных квантовых сенсоров. Таким образом, устойчивость запутанности открывает новые перспективы для практического применения квантовых явлений и стимулирует дальнейшие исследования в области квантовой информации.

Понимание динамического поведения запутанности имеет решающее значение для реализации потенциала квантовых технологий будущего. Исследования показывают, что способность запутанных состояний сохранять и даже усиливаться в определенных процессах, таких как автодистилляция, открывает новые возможности для повышения эффективности квантовых вычислений и коммуникаций. Оптимизация управления запутанностью позволит создавать более устойчивые к ошибкам квантовые схемы, что критически важно для масштабирования квантовых процессоров. Более того, глубокое понимание принципов, управляющих динамикой запутанности, таких как Stochastic Local Operations and Classical Communication (SLOCC), необходимо для разработки новых протоколов квантовой связи и создания защищенных от прослушивания каналов передачи информации. Таким образом, изучение этой области является ключевым шагом на пути к практическому применению квантовых технологий и раскрытию их огромного потенциала.

Исследование демонстрирует, что квантовая запутанность, проявляющаяся в процессах распада гиперонов, не является статичным свойством, а динамически изменяется в зависимости от параметров распада. Это согласуется с идеей о том, что попытки директивного управления сложными системами часто приводят к непредсказуемым результатам. Как заметил Сёрен Кьеркегор: «Жизнь — это не проблема, которую нужно решить, а реальность, которую нужно испытать». Аналогично, предложенный в статье механизм ‘автодистилляции запутанности’ указывает на то, что порядок и усиление квантовых корреляций возникают не из внешнего контроля, а как следствие внутренних правил и эволюции системы. Данный процесс, описанный в работе, подчеркивает, что глобальные закономерности, такие как усиление запутанности, возникают из простых, локальных правил распада частиц.

Что дальше?

Представленная работа, исследуя перераспределение запутанности в процессах распада гиперонов, лишь намекает на сложность динамики квантовых корреляций. Утверждение о возможности “самодистилляции” запутанности, хотя и интригующее, требует дальнейшей проверки в более реалистичных сценариях. Неизбежно возникает вопрос: насколько универсален этот механизм? Действительно ли локальные правила распада, определяя поведение отдельных частиц, способны породить глобальные паттерны устойчивой запутанности, или же наблюдаемый эффект — случайное следствие конкретных параметров?

Очевидным ограничением является упрощенность модели. Реальные процессы распада подвержены влиянию множества факторов — спинов, поляризаций, внешних полей. Учет этих факторов не просто усложнит вычисления, но и может радикально изменить картину перераспределения запутанности. Вероятно, наблюдаемая «устойчивость» является лишь временным состоянием, иллюзией контроля в системе, подверженной постоянным флуктуациям.

Вместо стремления к жесткому управлению запутанностью, более продуктивным представляется исследование возможностей слабого влияния. Необходим переход от поиска «идеальных» параметров к пониманию, как локальные правила, действующие на уровне отдельных распадов, могут способствовать эволюции квантовых корреляций, даже в условиях неполного контроля. Порядок не нуждается в архитекторе; он возникает из локальных правил, а слабый контроль сверху лишь поддерживает эту эволюцию.

Оригинал статьи: https://arxiv.org/pdf/2602.10398.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-13 00:21