Квантовые спиновые системы: Новый подход к поиску основного состояния

Автор: Денис Аветисян

Исследование эффективности суперпозиции прядежных состояний в задачах оптимизации и моделирования квантовых систем.

В исследовании продемонстрировано, что вариационный подход SPS избегает проблемы «пустых плато», обеспечивая эффективную оптимизацию даже для крупных квантовых систем, что подтверждается анализом градиентов локальных наблюдаемых по вариационным параметрам на 10 000 случайных выборках, где градиенты по коэффициентам $c_m$ оказываются идентичными для всех $m$, а при фиксированном $m=1$ – исчезают везде, кроме сайта приложения наблюдаемой, при этом дисперсии градиентов уменьшаются и насыщаются с увеличением размера системы $L$ и убывают полиномиально с ростом числа состояний продукта $M^2$.

В данной работе представлен и исследован вариационный подход, основанный на суперпозиции прядежных состояний (SPS), для поиска основного состояния квантовых спиновых систем в одном, двух и трех измерениях.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал

Несмотря на значительные успехи в изучении многочастичных квантовых систем, эффективный поиск основного состояния остается сложной задачей, особенно в высоких размерностях. В работе ‘Exploring the performance of superposition of product states: from 1D to 3D quantum spin systems’ исследуется производительность вариационного подхода, основанного на суперпозиции произведений состояний (SPS), как альтернативы тензорным сетям. Показано, что SPS-анзац обладает рядом преимуществ, включая точность извлечения информации, независимость от геометрии системы и возможности распараллеливания, достигая высокой точности в поиске основного состояния для различных моделей, от одномерных до трехмерных. Сможет ли этот подход стать эффективным инструментом для решения задач квантовой физики конденсированного состояния и расширить границы применимости вариационных квантовых алгоритмов?

Происхождение Порядка из Локальных Взаимодействий

Квантовые задачи, описывающие взаимодействие многих тел, характеризуются высокой вычислительной сложностью из-за экспоненциального роста требуемых ресурсов с увеличением системы. Это затрудняет точное моделирование даже умеренно сложных систем. Вариационные методы предлагают перспективный подход, позволяющий аппроксимировать основные состояния системы с помощью параметризованных пробных функций (анзацев). Суть метода заключается в минимизации энергетического функционала по параметрам анзаца, что позволяет получить приближенное основное состояние с минимальной энергией. Выбор подходящего анзаца критически важен, поскольку он должен обеспечивать баланс между выразительностью и вычислительной доступностью. Анзац, основанный на суперпозиции произведений состояний (SPS), демонстрирует многообещающие результаты, предоставляя эффективный способ аппроксимации сложных квантовых состояний с приемлемыми вычислительными затратами.

Тензорные Сети: Эффективное Представление Сложности

Алгоритмы тензорных сетей предоставляют мощную основу для представления квантовых состояний, используя сети взаимосвязанных тензоров. Этот подход позволяет эффективно кодировать информацию о многочастичных квантовых системах, что особенно важно при моделировании сложных систем. Эти методы используют внутренние корреляции в квантовых системах для снижения вычислительных затрат. Вместо обработки экспоненциально растущего вектора состояния, алгоритмы тензорных сетей оперируют тензорами меньшего размера, сохраняя ключевые физические свойства системы. Это достигается за счет представления волновой функции в виде сети тензоров, где каждый тензор описывает корреляции между небольшим числом частиц. Методы, такие как CornerTransferMatrixRenormalizationGroup и BoundaryMPS, расширяют базовый подход тензорных сетей для работы с более сложными системами и геометриями. SPS анзац демонстрирует производительность, сравнимую с DMRG в определенных конфигурациях, предоставляя конкурентоспособную альтернативу для моделирования одномерных и квази-одномерных систем.

Преодоление Проблемы «Исчезающих Градиентов»

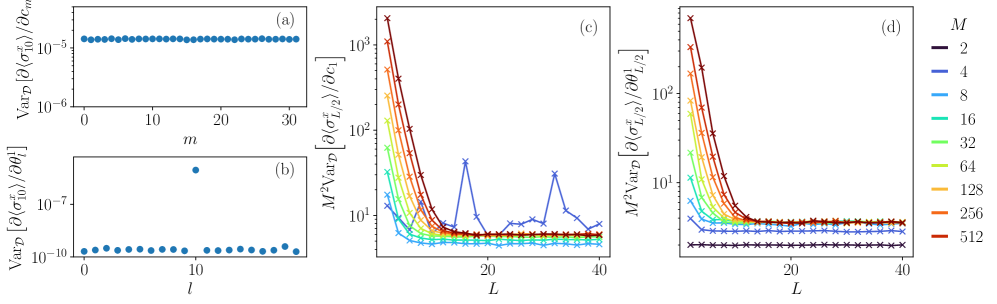
Оптимизация параметров вариационного анзаца имеет решающее значение для получения точных результатов в квантовых вычислениях. Однако практическая реализация часто сталкивается с трудностями, связанными с высокой размерностью пространства параметров. В пространствах параметров высокой размерности оптимизационный ландшафт может быть усеян «пустыми плато» – областями, где градиенты исчезают, препятствуя обучению. Это явление, известное как проблема «исчезающих градиентов», существенно ограничивает применимость вариационных алгоритмов к сложным задачам. Концепции, такие как RestrictedTypicality, направлены на решение этой проблемы путем выявления анзацев, демонстрирующих устойчивость и облегчающих эффективную оптимизацию. В частности, анзац SPS демонстрирует уменьшение дисперсии градиентов, полиномиально зависящее от $M$, что подтверждает его обучаемость и позволяет избежать «пустынных плато».

Масштабирование к Реалистичным Системам

Модель TiltedIsingModel, расширяющаяся до RandomCouplingNetwork и включающая взаимодействия дальнего радиуса действия, предоставляет универсальную платформу для тестирования квантовых алгоритмов. Этот подход позволяет исследовать широкий спектр физических систем, варьируя параметры модели и сложность сетевых взаимодействий. Методы, такие как DMRG, успешно применяются к этим моделям, демонстрируя эффективность тензорных сетей в решении нетривиальных квантовых задач. Достигнутая точность позволяет исследовать квантовые фазы и критические явления в системах с различной размерностью и сложностью. Понимание взаимосвязи между сложностью модели и производительностью алгоритма критически важно для развития области квантового моделирования. SPS анзац обеспечивает относительные ошибки до $10^{-8}$ при аппроксимации основного состояния в этих моделях, подтверждая его эффективность в задачах поиска основного состояния.

Математические Основы и Перспективы Развития

Эффективность современных методов приближенного моделирования квантовых систем напрямую зависит от математических свойств выбранного анзаца, часто укорененных в разложении Канноника-Полиадическом. Правильный выбор анзаца позволяет эффективно представить волновые функции, сохраняя при этом вычислительную доступность. Меры, такие как 2-Реньи энтропия ($S_2$), могут предоставить информацию о структуре запутанности в моделируемых состояниях и служить ориентиром при разработке анзацев. Анализ распределения 2-Реньи энтропии позволяет оценить качество аппроксимации и выявить области, требующие улучшения.

Figure 3:Typical 2-Rényi entropies obtained from 10,000 random SPS samples. (a) The distribution of the typical 2-Rényi entropies forL=20L=20. The entropies typically concentrate far from the theoretical maximum, even asMMincreases. (b) The minimum relative errors from the theoretical maximum saturate for largerLL.

Исследование потенциала NeuralQuantumStates и других подходов, вдохновленных машинным обучением, открывает захватывающие возможности для преодоления ограничений традиционных методов. В частности, анзац SPS демонстрирует вычислительную сложность $O(LM^2)$ для вычисления локальных наблюдаемых, что позволяет проводить эффективное моделирование.

Исследование демонстрирует, что эффективность поиска основного состояния квантовой системы напрямую зависит от способности волновой функции адаптироваться к локальным взаимодействиям. Принцип самоорганизации, лежащий в основе предложенного подхода с использованием суперпозиции произведения состояний (SPS), позволяет системе находить оптимальные решения без централизованного управления. Как отмечал Ричард Фейнман: «Если вы хотите действительно понять что-либо, то нужно сначала понять, что вы ничего не понимаете». Данное исследование подтверждает эту мысль, показывая, что отказ от жестких архитектур и переход к локальным правилам взаимодействия позволяет достичь удивительной эффективности в поиске оптимальных состояний сложной квантовой системы. Каждая точка связи в системе вносит свой вклад, формируя общее поведение, что соответствует идее влияния как реальной формы управления.

Что дальше?

Предложенный подход, использующий суперпозицию произведения состояний, демонстрирует способность к самоорганизации в поиске основного состояния. Это напоминает формирование кораллового рифа: локальные правила взаимодействия частиц, подобно полипам, приводят к возникновению сложной, упорядоченной структуры. Однако, иллюзия полного контроля над этой структурой обманчива. Оптимизация, как и эволюция, не стремится к заранее заданному идеалу, а скорее исследует ландшафт возможностей, находя компромиссы и локальные минимумы.

Ограничения текущего подхода, связанные с масштабируемостью и выразительностью, не являются препятствиями, а скорее приглашением к креативу. Дальнейшие исследования должны быть направлены на разработку более эффективных схем оптимизации, учитывающих специфику ландшафта энергии, и на комбинирование SPS с другими вариационными анзацами, такими как тензорные сети. Поиск способов адаптации структуры SPS к конкретной задаче, подобно тому, как ветви дерева подстраиваются под ветер, представляется особенно перспективным направлением.

В конечном счете, успех этого подхода, как и любого другого в квантовой теории многих тел, будет зависеть не от возможности полного контроля над системой, а от способности использовать ее внутреннюю сложность для решения практически значимых задач. Иногда, отказ от иллюзии контроля открывает путь к неожиданным и плодотворным решениям.

Оригинал статьи: https://arxiv.org/pdf/2511.08407.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2025-11-12 12:45