Квантовые траектории: ускорение восстановления симметрии под воздействием измерений

Автор: Денис Аветисян

Новое исследование показывает, что локальные измерения могут значительно ускорить процесс восстановления симметрии в квантовых системах с открытыми траекториями, в зависимости от начального состояния системы.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал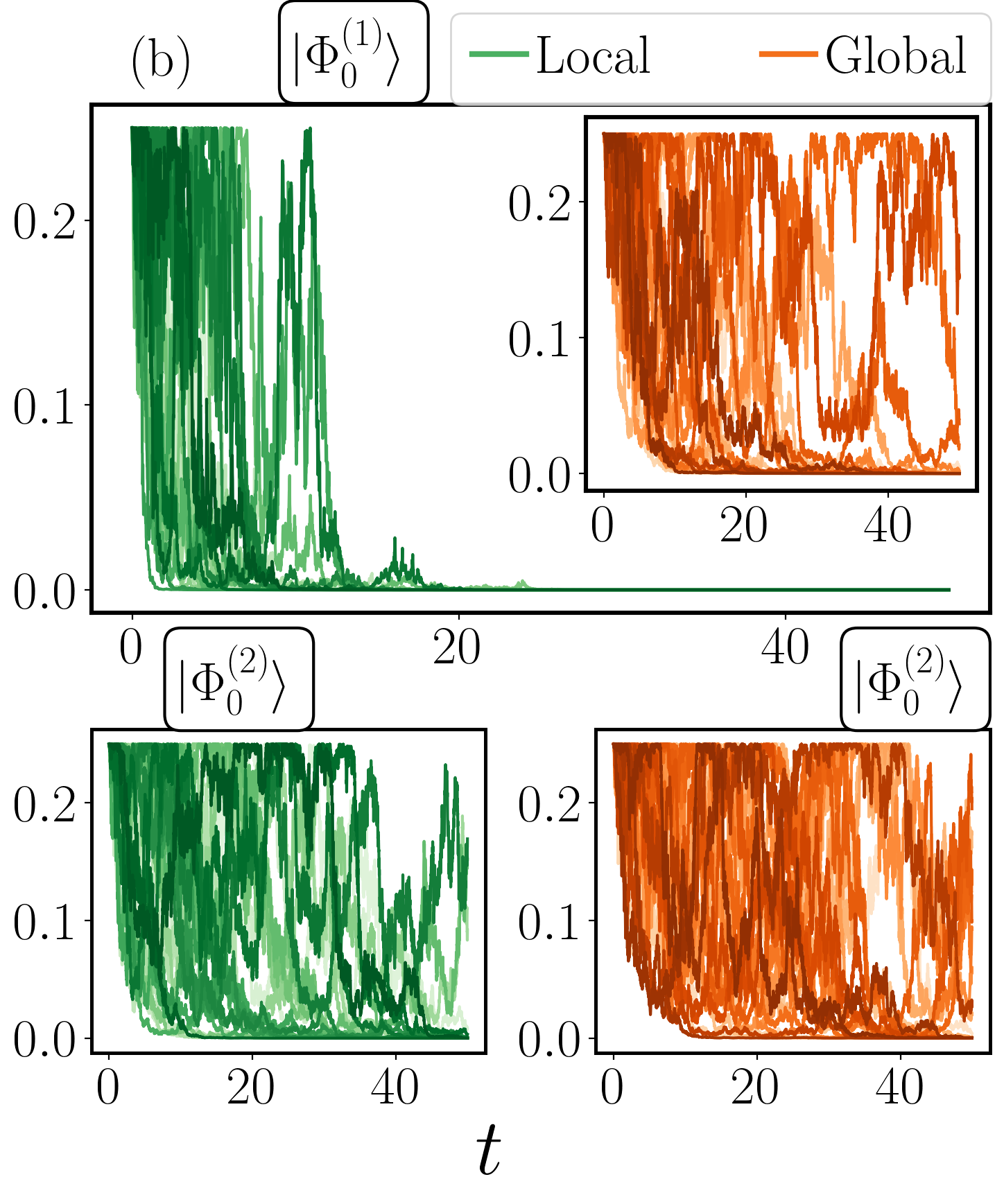

Наблюдения показывают, что при использовании протокола QSD (<span class="katex-eq" data-katex-display="false">\text{Eq. (10)}</span>) с параметрами <span class="katex-eq" data-katex-display="false">L=5</span>, <span class="katex-eq" data-katex-display="false">\gamma=0.1</span>, <span class="katex-eq" data-katex-display="false">dt=0.01</span> и <span class="katex-eq" data-katex-display="false">J=0.001</span>, локальный мониторинг оператора <span class="katex-eq" data-katex-display="false">\hat{n}_i</span> приводит к более быстрой реставрации симметрии для начального состояния <span class="katex-eq" data-katex-display="false">|\Phi_0^{(1)}\rangle</span> по сравнению с глобальным мониторингом, в то время как для состояния <span class="katex-eq" data-katex-display="false">|\Phi_0^{(2)}\rangle</span> оба подхода демонстрируют эквивалентные временные рамки восстановления симметрии, что подтверждается анализом 100 траекторий. — Наблюдения показывают, что при использовании протокола QSD ( $\text{Eq. (10)}$ ) с параметрами $L=5$ , $\gamma=0.1$ , $dt=0.01$ и $J=0.001$ , локальный мониторинг оператора $\hat{n}_i$ приводит к более быстрой реставрации симметрии для начального состояния $|\Phi_0^{(1)}\rangle$ по сравнению с глобальным мониторингом, в то время как для состояния $|\Phi_0^{(2)}\rangle$ оба подхода демонстрируют эквивалентные временные рамки восстановления симметрии, что подтверждается анализом 100 траекторий.

Исследована зависимость скорости восстановления U(1) симметрии в квантовых траекториях от характера измерений и начальной запутанности системы.

Несмотря на значительный прогресс в понимании динамики открытых квантовых систем, вопрос о влиянии непрерывных измерений на восстановление симметрии остается недостаточно изученным. В работе «Measurement induced faster symmetry restoration in quantum trajectories» исследуется, как непрерывные измерения могут ускорить восстановление глобальной $U(1)$ -симметрии в квантовых траекториях. Показано, что скорость восстановления симметрии зависит от начального состояния системы, причем состояния с отдаленными секторами зарядов релаксируют быстрее, а локальные измерения могут дополнительно ускорить этот процесс. Какие новые стратегии контроля квантовых систем можно разработать, используя эффект ускоренного восстановления симметрии посредством измерений?

Открытые Квантовые Системы: Вызов Фундаментальной Теории

Описание динамики открытых квантовых систем, взаимодействующих с окружающей средой, представляет собой сложную задачу, обусловленную фундаментальными особенностями квантовой механики и экспоненциальным ростом сложности при увеличении числа взаимодействующих степеней свободы. В отличие от изолированных систем, эволюция которых описывается унитарными операторами, взаимодействие с окружающей средой приводит к декогеренции и диссипации, что выражается в появлении не-унитарных эффектов и требует учета бесконечного числа степеней свободы окружающей среды. $\rho(t) = U(t) \rho(0) U^{\dagger}(t)$ — стандартное уравнение эволюции для изолированных систем, становится неприменимым, поскольку описывает лишь идеализированный случай. Поэтому для адекватного моделирования открытых квантовых систем необходимы специальные подходы, такие как уравнения Линдблада или методы влияния функционала, которые, однако, часто сопряжены с упрощениями и приближениями, ограничивающими точность и область применимости.

Традиционные методы моделирования открытых квантовых систем, взаимодействующих с окружающей средой, зачастую сталкиваются с существенными ограничениями. Из-за сложности точного описания этих взаимодействий, исследователи вынуждены прибегать к различным приближениям. Эти приближения, хоть и позволяют получить хоть какие-то результаты, неизбежно приводят к потере точности или требуют огромных вычислительных ресурсов. Например, методы, основанные на теории возмущений, могут быть эффективны лишь для слабо связанных систем, а более точные подходы, такие как уравнения движения Линдблада, быстро становятся вычислительно непосильными даже для относительно небольших систем. В результате, возникает необходимость в разработке новых, более эффективных и точных методов для изучения динамики открытых квантовых систем, которые позволили бы преодолеть эти ограничения и приблизиться к реалистичному моделированию сложных квантовых процессов. $H = H_S + H_B + H_{SB}$

Понимание динамики открытых квантовых систем имеет решающее значение для прогресса в области квантовых технологий и фундаментальной физики. От квантовых вычислений и криптографии до разработки новых материалов и сенсоров, способность контролировать и предсказывать поведение квантовых систем, взаимодействующих с окружающей средой, является ключевой. Исследования в этой области позволяют разрабатывать более стабильные и эффективные кубиты, повышать точность квантовых измерений и создавать новые типы квантовых устройств. Кроме того, изучение открытых квантовых систем помогает глубже понять основополагающие принципы квантовой механики, такие как декогеренция и квантовая запутанность, что открывает новые горизонты в понимании природы реальности на микроскопическом уровне. $H = H_S + H_B + H_{SB}$ — такое представление гамильтониана открытой системы позволяет моделировать взаимодействие с окружением и искать пути к когерентности.

Моделирование квантовой диффузии состояний показывает, что начальные флуктуации числа частиц коррелируют со скоростью восстановления симметрии, при этом состояние с большими флуктуациями восстанавливает симметрию быстрее, а локальная намагниченность демонстрирует осцилляторное поведение после восстановления симметрии.

Траекторный Анализ: Раскрытие Динамики Непрерывным Измерением

Метод $QuantumTrajectory$ представляет собой эффективный инструмент для декомпозиции $QuantumMasterEquation$ на отдельные, стохастические траектории. В отличие от решения $QuantumMasterEquation$ , которое дает среднее поведение системы, метод $QuantumTrajectory$ позволяет отследить эволюцию квантового состояния через последовательность дискретных «снимков» состояния, полученных в моменты времени, определяемые непрерывными измерениями. Каждая траектория представляет собой возможный путь эволюции системы, учитывающий случайные «скачки», возникающие в результате взаимодействия с окружающей средой. Анализ ансамбля этих траекторий позволяет получить статистически полную картину динамики квантовой системы и исследовать влияние отдельных событий на её эволюцию.

Непрерывное измерение позволяет получить детальное представление о динамике квантовой системы, выходя за рамки анализа средних значений. В отличие от традиционных методов, которые оперируют с усредненными характеристиками, непрерывный мониторинг предоставляет информацию о траекториях эволюции системы во времени. Это достигается путем последовательного измерения наблюдаемой величины и использования полученных данных для корректировки волновой функции или вектора состояния. Такой подход позволяет выявить флуктуации и нелинейные эффекты, которые остаются скрытыми при анализе только средних значений, что особенно важно для понимания процессов декогеренции и релаксации в квантовых системах. Примером является возможность отслеживания отдельных квантовых траекторий, каждая из которых представляет собой возможный исход эволюции системы.

Для реализации непрерывного мониторинга квантовой системы применяются различные методы, среди которых выделяются диффузия квантового состояния (Quantum State Diffusion) и процесс квантовых скачков (Quantum Jump Process). Диффузия квантового состояния представляет собой стохастический процесс, в котором волновая функция системы непрерывно эволюционирует под воздействием случайного шума, описываемого дифференциальным уравнением. В свою очередь, процесс квантовых скачков моделирует дискретные изменения состояния системы, происходящие в моменты регистрации событий измерения. Выбор конкретного метода зависит от характера измеряемого наблюдаемой и требуемой точности моделирования динамики системы, при этом оба подхода позволяют получить траектории, описывающие эволюцию волновой функции во времени.

Выбор между глобальным (GlobalMonitoring) и локальным (LocalMonitoring) мониторингом определяется природой измеряемой наблюдаемой. Глобальный мониторинг предполагает непрерывное измерение оператора, действующего на всё гильбертово пространство системы, что позволяет отслеживать изменения во всей системе. Локальный мониторинг, напротив, фокусируется на измерении оператора, действующего только на подпространстве, соответствующем конкретному региону или подсистеме. В случае, когда интерес представляет корреляция между различными частями системы или общее изменение состояния, предпочтительнее использовать глобальный мониторинг. Если же необходимо отследить изменения в конкретной локальной области, например, для анализа траектории отдельной частицы, более эффективным является локальный мониторинг. Выбор также влияет на интерпретацию получаемых траекторий и на необходимые вычислительные ресурсы.

Непрерывный мониторинг оператора полной намагниченности <span class="katex-eq" data-katex-display="false"> \hat{S}_z </span> демонстрирует, что процесс квантовых скачков неэффективно восстанавливает U(1)-симметрию, в то время как процесс квантовой диффузии состояний эффективно восстанавливает симметрию и проявляет разделение временных масштабов при эволюции по гамильтониану <span class="katex-eq" data-katex-display="false"> H_S </span> с параметрами J=1 и Δ=0.1. — Непрерывный мониторинг оператора полной намагниченности $\hat{S}_z$ демонстрирует, что процесс квантовых скачков неэффективно восстанавливает U(1)-симметрию, в то время как процесс квантовой диффузии состояний эффективно восстанавливает симметрию и проявляет разделение временных масштабов при эволюции по гамильтониану $H_S$ с параметрами J=1 и Δ=0.1.

Нарушение и Восстановление Симметрии: Ключ к Пониманию Динамики

Многие квантовые системы обладают симметриями, описываемыми операторами, такими как $NumberOperator$ , который представляет собой оператор числа частиц. Эти операторы соответствуют сохраняющимся величинам системы и обеспечивают её стабильность. Симметрии проявляются в инвариантности системы относительно определенных преобразований, таких как сдвиг или вращение. Наличие симметрии существенно упрощает анализ системы, позволяя использовать соответствующие законы сохранения для определения её поведения и свойств. Нарушение симметрии, вызванное внешними воздействиями или внутренними процессами, может привести к изменению фазового состояния системы и появлению новых свойств.

Внешние возмущения способны приводить к нарушению симметрии квантовой системы, изменяя её свойства и потенциально вызывая переход в новое состояние. Данное нарушение симметрии проявляется в изменении собственных функций и энергетических уровней системы, что может приводить к появлению новых состояний, не существовавших ранее. Интенсивность и характер возмущения определяют степень нарушения симметрии и природу возникающих новых состояний. Нарушение симметрии не обязательно приводит к полной потере симметрии; возможно частичное нарушение, когда некоторые симметрии сохраняются, а другие разрушаются.

Непрерывные измерения квантовой системы могут приводить к изменению её симметрии, проявляясь в фазовых переходах, таких как $PurificationTransition$ и $ZenoPhaseTransition$ . $PurificationTransition$ возникает, когда непрерывное измерение оператора числа частиц приводит к подавлению состояний с высокой неопределенностью числа частиц, эффективно «очищая» состояние системы. $ZenoPhaseTransition$ , напротив, возникает из-за подавления динамики системы постоянными измерениями, «замораживающими» её в начальном состоянии и препятствующими переходу в другие. Оба перехода демонстрируют, что процесс измерения сам по себе может существенно влиять на эволюцию квантовой системы и приводить к качественно новым состояниям.

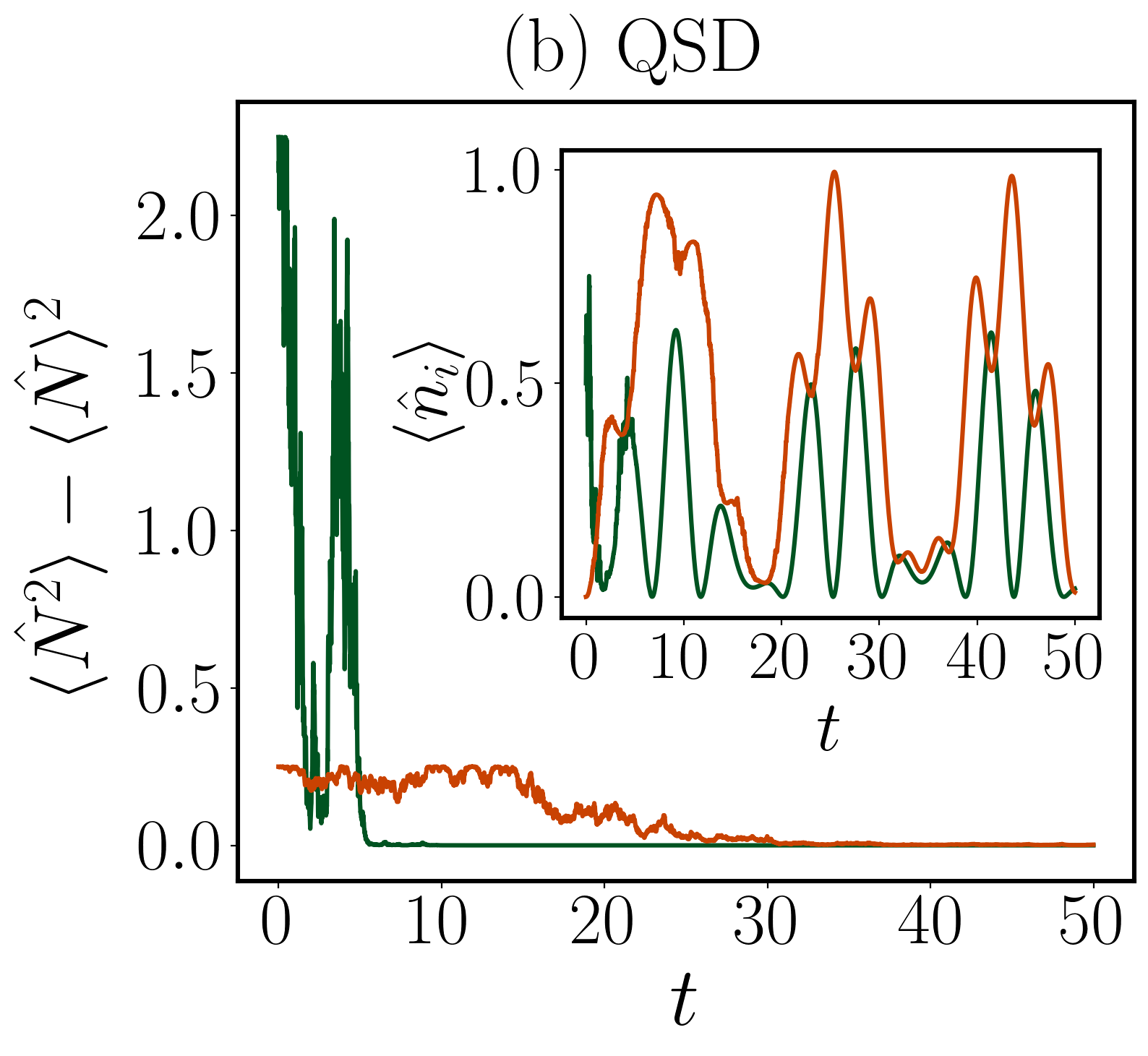
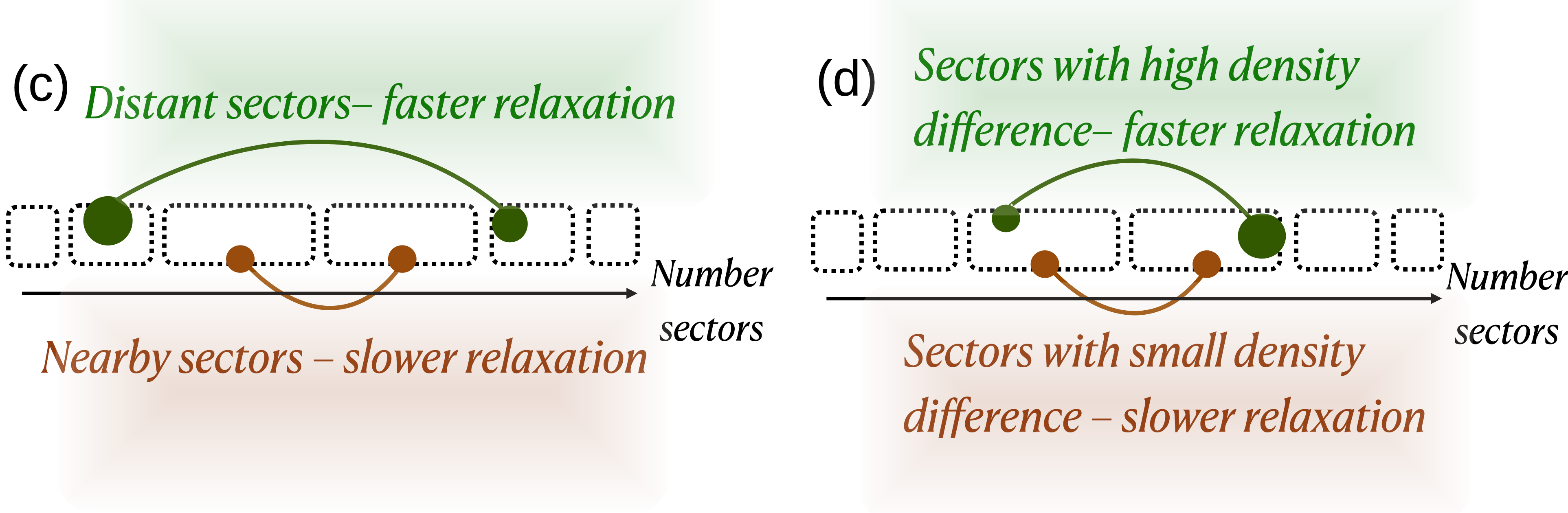
Восстановление симметрии в квантовых системах может происходить во время эволюции системы, что часто проявляется в изменениях $DensityProfile$ — профиля плотности частиц. Наши симуляции демонстрируют, что характерная шкала времени этого восстановления обратно пропорциональна разнице энергий между различными “числовыми секторами” системы. Другими словами, чем больше энергетический зазор между состояниями с разным числом частиц, тем быстрее происходит восстановление симметрии после возмущения. Это указывает на то, что динамика восстановления симметрии тесно связана с энергетическим спектром и структурой многочастичных состояний системы.

Непрерывный мониторинг глобального оператора полного числа спинов вверх <span class="katex-eq" data-katex-display="false">\hat{N}=\hat{S}_{z}+L/2</span> или локального оператора плотности <span class="katex-eq" data-katex-display="false">\hat{n}_{i}=\hat{S}_{z}^{i}+1/2</span> в одномерной спиновой решетке позволяет динамически восстановить симметрию <span class="katex-eq" data-katex-display="false">U(1)</span>, причем скорость восстановления зависит от распределения числа спинов: глобальный мониторинг эффективнее для состояний с удаленными секторами числа, а локальный - для состояний с большей разницей в плотности. — Непрерывный мониторинг глобального оператора полного числа спинов вверх $\hat{N}=\hat{S}_{z}+L/2$ или локального оператора плотности $\hat{n}_{i}=\hat{S}_{z}^{i}+1/2$ в одномерной спиновой решетке позволяет динамически восстановить симметрию $U(1)$ , причем скорость восстановления зависит от распределения числа спинов: глобальный мониторинг эффективнее для состояний с удаленными секторами числа, а локальный — для состояний с большей разницей в плотности.

Ускоренная Динамика и Роль Измерений: Новый Взгляд на Неравновесные Системы

Непрерывные измерения способны значительно ускорить возврат системы к равновесному состоянию, что приводит к более быстрой релаксации по сравнению с изолированными системами. Этот эффект обусловлен тем, что постоянное наблюдение за системой, фактически, влияет на её динамику, «подталкивая» к состоянию наименьшей энергии. Вместо того чтобы позволить системе эволюционировать естественным путем, измерения создают своего рода «канал», по которому энергия быстрее рассеивается. В результате, время, необходимое для достижения равновесия, сокращается, что особенно заметно в квантовых системах, где процесс релаксации может быть значительно замедлен из-за когерентности и запутанности. Изучение подобных процессов открывает возможности для управления динамикой систем и достижения равновесия в более короткие сроки, что имеет важное значение для различных областей науки и техники.

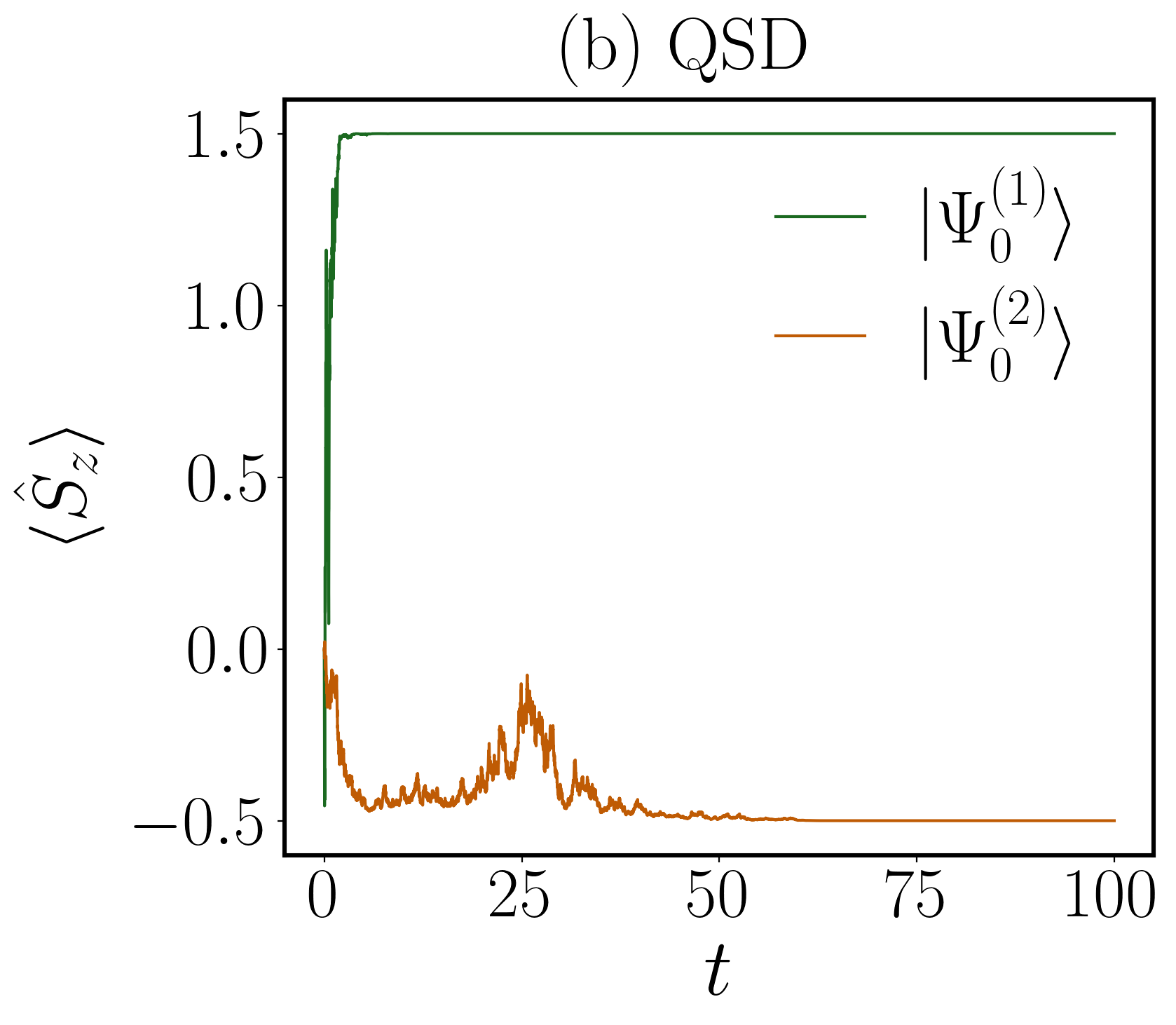
Исследования демонстрируют, что взаимодействие между измерением, восстановлением симметрии и начальным состоянием системы играет ключевую роль в динамике релаксации. Особо выделяется влияние разделения между секторами чисел состояний: чем больше это разделение в начальном состоянии, тем быстрее происходит восстановление симметрии. Анализ асимметрии энтропии подтверждает эту закономерность, позволяя количественно оценить скорость восстановления симметрии в зависимости от начальной конфигурации. Наблюдаемый эффект указывает на то, что измерение не просто пассивно фиксирует состояние системы, но активно влияет на её эволюцию, ускоряя переход к равновесию, особенно в случаях, когда начальное состояние существенно отличается от симметричного.

Изменения в переходах запутанности, или $EntanglementTransitions$ , служат важными индикаторами динамических процессов, происходящих в системе, и позволяют выявить её неравновесное состояние. Наблюдение за тем, как меняется степень запутанности между различными частями системы во времени, предоставляет информацию о скорости и характере релаксации к равновесию. В частности, резкие изменения в запутанности могут указывать на фазовые переходы или другие критические явления, происходящие в системе. Анализ этих переходов позволяет не только констатировать неравновесность системы, но и понять механизмы, управляющие её эволюцией, раскрывая взаимосвязь между запутанностью, симметрией и динамикой.

Для детального изучения ускоренной динамики и роли измерений используется модель $XX$ -гамильтониана, учитывающая взаимодействия и магнитный момент системы. Исследования показывают, что для начальных состояний, таких как $|Φ₀(1)⟩$ , локальный мониторинг существенно ускоряет восстановление симметрии по сравнению с глобальным. Это связано с тем, что локальные измерения более эффективно подавляют когерентные колебания между различными секторами чисел, способствуя более быстрому переходу к равновесному состоянию. Данный подход позволяет изучать влияние характера измерений на динамику не-равновесных систем и проливает свет на фундаментальные аспекты взаимодействия между наблюдателем и системой.

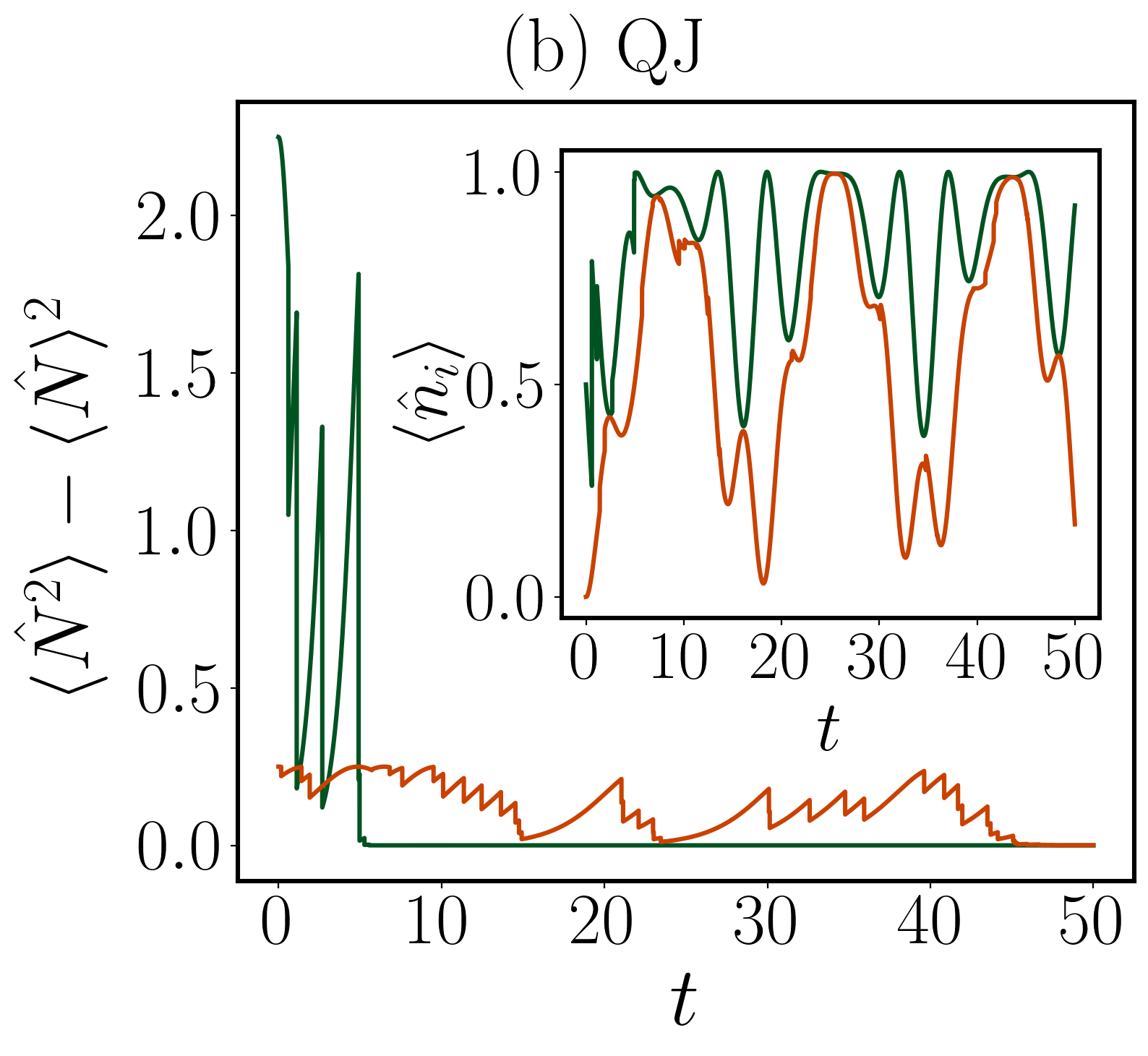
Анализ динамики общего числа спинов, направленных вверх <span class="katex-eq" data-katex-display="false">\langle N \rangle = \langle S^z \rangle + L/2</span>, и флуктуаций этого числа показывает, что начальное состояние с большей флуктуацией восстанавливает симметрию быстрее, при этом динамика локального оператора числа спинов <span class="katex-eq" data-katex-display="false">\langle \hat{n}_i \rangle = \hat{S}_z^i + 1/2</span> на сайте i=3 демонстрирует осцилляторное поведение после восстановления симметрии, что не зависит от конкретной формы гамильтониана решетки при <span class="katex-eq" data-katex-display="false">L=5</span>, <span class="katex-eq" data-katex-display="false">\gamma=0.1</span>, <span class="katex-eq" data-katex-display="false">dt=0.01</span>. — Анализ динамики общего числа спинов, направленных вверх $\langle N \rangle = \langle S^z \rangle + L/2$ , и флуктуаций этого числа показывает, что начальное состояние с большей флуктуацией восстанавливает симметрию быстрее, при этом динамика локального оператора числа спинов $\langle \hat{n}_i \rangle = \hat{S}_z^i + 1/2$ на сайте i=3 демонстрирует осцилляторное поведение после восстановления симметрии, что не зависит от конкретной формы гамильтониана решетки при $L=5$ , $\gamma=0.1$ , $dt=0.01$ .

Исследование демонстрирует, что динамика восстановления симметрии в квантовых траекториях тесно связана с начальным состоянием системы и типом проводимых измерений. Особенно важно отметить, что локальные измерения способны ускорить этот процесс по сравнению с глобальными. Это согласуется с глубоким пониманием взаимосвязанности элементов в любой системе, где изменение одной части неизбежно влечет за собой цепную реакцию. Как однажды заметила Мария Кюри: «Никогда нельзя сказать, куда приведет то или иное исследование, если не понять всю систему». Акцент на ускоренной релаксации при локальных измерениях подчеркивает, что эффективное управление сложными квантовыми системами требует детального анализа архитектуры и взаимодействия их компонентов, а не только фокусировки на отдельных аспектах.

Куда Ведет Этот Путь?

Представленные результаты, демонстрирующие зависимость скорости восстановления симметрии от начального состояния и природы измерений, лишь подчеркивают фундаментальную сложность открытых квантовых систем. Вместо того, чтобы стремиться к все более точным описаниям релаксации, представляется более плодотворным сосредоточиться на понимании тех случаев, когда эта релаксация не происходит. Или, иными словами, на поиске условий, при которых сохранение информации превосходит неизбежное влияние измерений. Наблюдаемое ускорение восстановления симметрии локальными измерениями — любопытный эффект, но не стоит забывать, что оптимизация скорости — не всегда оптимальное решение.

Следующим шагом видится переход от рассмотрения отдельных траекторий к анализу ансамблевых свойств. Понимание того, как различные типы корреляций возникают и эволюционируют под влиянием непрерывных измерений, представляется более важным, чем точное определение времени восстановления симметрии для конкретного начального состояния. Иначе, рискуем потратить усилия на решение несущественных задач, упуская из виду общую картину.

Неизбежно возникает вопрос о масштабируемости. Предложенные методы анализа применимы к системам с малым числом частиц. Расширение этих методов на более сложные системы, с большим числом степеней свободы, потребует разработки новых, более эффективных вычислительных алгоритмов и, возможно, пересмотра некоторых фундаментальных принципов. Зависимости, как известно, — настоящая цена свободы, и в данном случае, они могут оказаться непомерно высокими.

Оригинал статьи: https://arxiv.org/pdf/2601.18458.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-28 02:05