Квантовые узоры: Как неупорядоченность меняет поведение неэрмитовых систем

Автор: Денис Аветисян

Новое исследование показывает, что введение квазипериодичности в неэрмитовые системы может приводить к переходу от локализованных состояний к эффекту неэрмитовой кожи или расширенным состояниям.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал

В данной модели изучается влияние асимметричного скачка <span class="katex-eq" data-katex-display="false">J e^{\pm\alpha}</span>, квазипериодического потенциала на месте <span class="katex-eq" data-katex-display="false">\lambda_j</span> и настраиваемой силы скачка примеси μ на поведение системы, демонстрируя возможность тонкой настройки её характеристик за счёт управления этими параметрами. — В данной модели изучается влияние асимметричного скачка $J e^{\pm\alpha}$ , квазипериодического потенциала на месте $\lambda_j$ и настраиваемой силы скачка примеси μ на поведение системы, демонстрируя возможность тонкой настройки её характеристик за счёт управления этими параметрами.

Исследование демонстрирует взаимосвязь между квазипериодичностью, обобщенными граничными условиями и разрушением масштабной локализации в неэрмитовых системах.

Необычная чувствительность к граничным условиям является характерной чертой неэрмитовых систем, однако механизмы, управляющие этой чувствительностью, остаются недостаточно изученными. В работе, озаглавленной ‘Quasiperiodicity-induced non-Hermitian skin effect from the breakdown of scale-free localization’, исследуется влияние квазипериодического беспорядка на неэрмитовую решетку с изменяемым связыванием на границе. Показано, что квазипериодичность приводит к разрушению режима масштабной локализации, вызывая переход либо к неэрмитовому скин-эффекту, либо к расширенному режиму, в зависимости от граничных условий. Какова роль квазипериодичности в формировании топологических свойств и динамики неэрмитовых систем?

За пределами стандартных рамок: Рождение неэрмитовой физики

Традиционная физика конденсированного состояния долгое время опиралась на использование эрмитовых гамильтонианов, что позволяло эффективно описывать изолированные системы. Однако, такое ограничение не позволяет адекватно моделировать реальные физические системы, которые неизбежно взаимодействуют с окружающей средой, испытывают потери энергии или, наоборот, получают её извне. Эрмитовость гарантирует сохранение вероятности, но в открытых системах, где происходит обмен энергией и частицами, это условие нарушается. В результате, стандартный формализм оказывается неспособен описать такие явления, как усиление сигнала в лазерах, диссипацию энергии в несовершенных материалах или поведение метаматериалов с активными элементами. Преодоление этого ограничения требует перехода к неэрмитовым гамильтонианам, открывая новые возможности для понимания и контроля над поведением сложных систем и материалов.

Негерметичная физика расширяет традиционные рамки, позволяя исследовать системы, в которых присутствуют как усиление, так и потери энергии. В отличие от стандартных моделей, предполагающих сохранение энергии, негерметичные системы могут обмениваться энергией с окружающей средой, что приводит к появлению уникальных явлений. Такие системы демонстрируют необычные свойства, например, асимметричное распространение волн, топологические состояния, устойчивые к рассеянию, и модифицированные спектральные характеристики. Изучение этих эффектов открывает новые возможности для создания устройств с улучшенными характеристиками, включая лазеры с повышенной эффективностью, сенсоры с высокой чувствительностью и новые типы оптических материалов. Ключевым аспектом является то, что негерметичность позволяет описывать процессы, которые ранее считались невозможными или слишком сложными для анализа, тем самым углубляя понимание фундаментальных физических принципов.

Расширение стандартных границ физики, позволяющее учитывать негермитовы системы, имеет решающее значение для адекватного описания широкого спектра физических явлений. Большинство реальных систем не изолированы, а подвержены воздействию внешних факторов или взаимодействуют с окружающей средой, что приводит к потерям или, наоборот, к усилению энергии. Такие процессы, игнорируемые в традиционных подходах, оказывают существенное влияние на поведение системы, формируя необычные эффекты, такие как асимметричные спектры, топологические фазы и нетрадиционные транспортные свойства. Изучение негермитовых систем, таким образом, открывает путь к более полному пониманию динамики открытых систем и позволяет разрабатывать новые материалы и устройства с улучшенными характеристиками, учитывающие неизбежные взаимодействия с внешним миром.

Не-эрмитовский эффект «кожи»: Новая форма локализации

Не-эрмитовский эффект “кожи” проявляется в экспоненциальной локализации собственных состояний на границах системы. Это означает, что вероятность обнаружения частицы вблизи границ системы значительно выше, чем в её центре, и эта вероятность убывает экспоненциально при удалении от границы. Математически, это выражается в том, что собственные функции системы концентрируются у границ, а их амплитуда быстро затухает вглубь системы. Данный эффект является прямым следствием не-эрмитовской природы гамильтониана, который допускает комплексные собственные значения и, как следствие, ненормальные собственные функции, отличные от ортогональных в эрмитовых системах. Локализация характеризуется длиной локализации, которая определяет, насколько быстро происходит затухание амплитуды волновой функции от границы.

Эффект неэрмитового скин-эффекта обусловлен нереципрокным переносом, при котором вероятность перехода между узлами решетки зависит от направления. В стандартных эрмитовых системах вероятность перемещения из узла i в узел j равна вероятности обратного перехода из j в i. Однако, в неэрмитовых системах, описываемых, например, моделью Хатано-Нельсона, эти вероятности могут быть различными. Это асимметричное перескок приводит к тому, что собственные функции системы экспоненциально локализуются на границах, в отличие от распространенной в эрмитовых системах локализации, обусловленной случайными дефектами или потенциальными барьерами. Различие в вероятностях перескоков формирует направленный поток вероятности, который накапливается на краях системы, приводя к специфическому типу локализации.

Модель Хатано-Нельсона является ключевым примером, демонстрирующим, как неравновесность (non-reciprocity) в системе приводит к уникальной локализации собственных состояний на границах. В данной модели, амплитуда вероятности перехода между соседними узлами решетки различна в зависимости от направления — вероятность перехода в одну сторону отличается от вероятности перехода в противоположную. $t_{ij} \neq t_{ji}$ , где $t_{ij}$ — амплитуда перехода от узла i к узлу j. Это приводит к экспоненциальному затуханию волновой функции при удалении от границы, что и является характерной чертой эффекта неэрмитовой кожи. Конкретно, в модели Хатано-Нельсона, неравновесность в переходах является достаточным условием для возникновения данной локализации, что делает её важным инструментом для изучения и понимания этого явления.

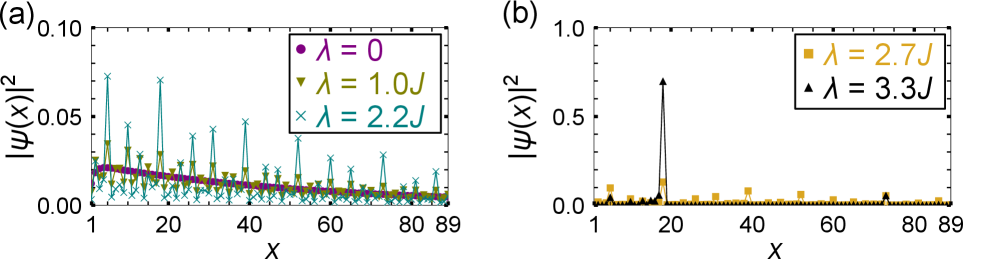
Длина локализации в неэрмитовых системах, демонстрирующих эффект неэрмитовой кожи, претерпевает существенные изменения по сравнению с эрмитовыми аналогами. Наблюдается переход от степенного закона убывания волновой функции, характерного для систем с $L=89$ , к экспоненциальному затуханию вблизи границ системы. Это указывает на фундаментальное изменение поведения волновой функции, а также на то, что собственные состояния системы экспоненциально локализуются у границ, что существенно влияет на транспортные свойства и другие наблюдаемые величины. Значение длины локализации напрямую связано с интенсивностью экспоненциального затухания и характеризует степень концентрации волновой функции у границы.

При <span class="katex-eq" data-katex-display="false">L=89</span> и <span class="katex-eq" data-katex-display="false">ln\mu = -0.5</span>, пространственное распределение плотности вероятности <span class="katex-eq" data-katex-display="false">|\psi(x)|^{2}</span> демонстрирует как протяженные, так и локализованные состояния, различающиеся в зависимости от характера волновой функции. — При $L=89$ и $ln\mu = -0.5$ , пространственное распределение плотности вероятности $|\psi(x)|^{2}$ демонстрирует как протяженные, так и локализованные состояния, различающиеся в зависимости от характера волновой функции.

Диагностика эффекта «кожи»: Числа обусловленности и ненормальность

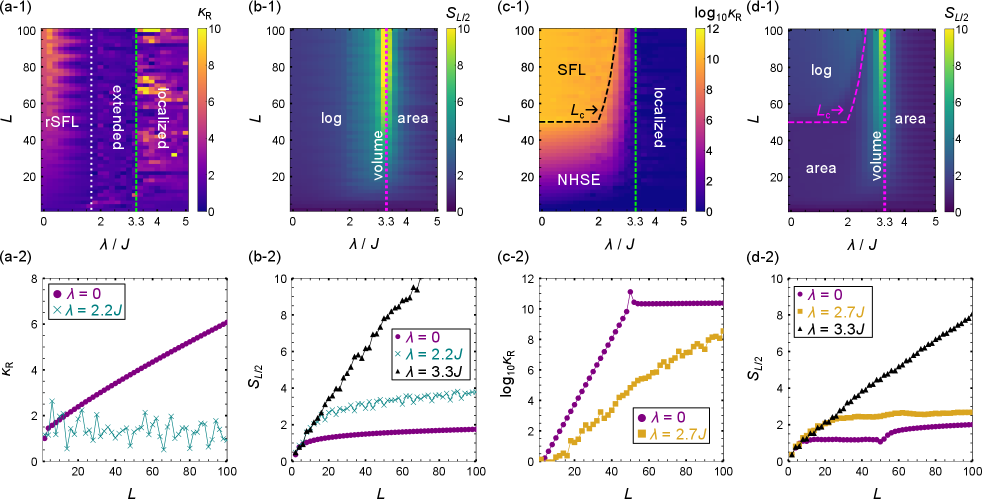
Число обусловленности (Condition Number) является количественной мерой не-нормальности оператора, и эффективно указывает на наличие и выраженность Не-Эрмитового Эффекта Скин (Non-Hermitian Skin Effect). Не-нормальность возникает, когда левые и правые собственные векторы оператора не совпадают, что приводит к экспоненциальному росту или затуханию возмущений. Большое число обусловленности κ указывает на сильную не-нормальность и, следовательно, на ярко выраженный Эффект Скин, при котором состояния локализованы на краях системы. В то время как традиционные методы анализа локализации требуют вычисления волновых функций, число обусловленности предоставляет прямой и вычислительно эффективный способ определения наличия и силы этого эффекта, позволяя оценивать чувствительность системы к возмущениям без явного решения уравнения Шредингера.

Коэффициент ненормальности (Non-Normality Ratio) представляет собой эффективный инструмент для дифференциации различных режимов локализации в системах, подверженных эффекту неэрмитовой кожи. Этот коэффициент анализирует чувствительность системы к возмущениям и демонстрирует зависимость масштабирования от длины локализации ξ. В частности, величина коэффициента ненормальности позволяет количественно оценить степень локализации и определить, преобладает ли экспоненциальная или полиномиальная зависимость от длины локализации, что важно для классификации различных типов локализационных режимов и прогнозирования поведения системы при малых возмущениях.

Использование показателей, таких как число обусловленности и коэффициент ненормальности, позволяет проводить надежную и количественную оценку эффекта не-эрмитового скин-эффекта, избегая сложных вычислений волновой функции. Традиционные методы анализа локализации, требующие прямого расчета $\Psi(x)$ , могут быть вычислительно затратными, особенно в системах с большим числом параметров или сложной геометрией. Данные показатели предоставляют альтернативный подход, основанный на анализе матричных свойств гамильтониана, что существенно упрощает и ускоряет диагностику скин-эффекта и позволяет оценить его силу без необходимости вычисления полного спектра волновых функций.

Данный подход к диагностике эффекта «не-эрмитовой кожи» особенно ценен в системах, где традиционный анализ локализации требует значительных вычислительных ресурсов. Вычисление волновых функций и определение степеней локализации часто связано с экспоненциальным ростом сложности по мере увеличения размера системы. Использование таких показателей, как число обусловленности и коэффициент ненормальности, позволяет количественно оценить эффект «кожи» без необходимости проведения трудоемких расчетов волновых функций, что делает его применимым к более крупным и сложным системам, где прямые методы оказываются непрактичными или недоступными. Это особенно актуально для исследования систем с беспорядком, сложной геометрией или многомерными структурами.

Анализ диаграмм, основанных на коэффициенте ненормальности и энергии эффективного сдвига (EE), на плоскости <span class="katex-eq" data-katex-display="false">(\lambda, L)</span>, показывает, что поведение коэффициента ненормальности <span class="katex-eq" data-katex-display="false">\kappa_R</span> и энергии эффективного сдвига <span class="katex-eq" data-katex-display="false">EESL/2</span> масштабируется в зависимости от <span class="katex-eq" data-katex-display="false">\ln\mu</span>, причём критическая длина <span class="katex-eq" data-katex-display="false">L_c</span>, оценённая по данным из Fig. 2(a-1), согласуется с наблюдаемым поведением. — Анализ диаграмм, основанных на коэффициенте ненормальности и энергии эффективного сдвига (EE), на плоскости $(\lambda, L)$ , показывает, что поведение коэффициента ненормальности $\kappa_R$ и энергии эффективного сдвига $EESL/2$ масштабируется в зависимости от $\ln\mu$ , причём критическая длина $L_c$ , оценённая по данным из Fig. 2(a-1), согласуется с наблюдаемым поведением.

Настраиваемая локализация: Обобщённые граничные условия

Введение обобщенных граничных условий предоставляет уникальную возможность плавно переходить между двумя крайними случаями: открытыми и периодическими граничными условиями. Традиционно, эти условия рассматриваются как дискретные варианты, определяющие поведение волновых функций в ограниченной области. Однако, используя обобщенные условия, становится возможным непрерывно изменять характер граничных взаимодействий, что позволяет детально исследовать переход между локализованными и делокализованными состояниями. Такой подход не только расширяет возможности моделирования различных физических систем, но и открывает путь к управлению свойствами систем, например, к созданию материалов с заданными характеристиками локализации. $\psi(x=0) = a\psi(0) + b\psi'(0)$ — типичное выражение обобщенного граничного условия, где параметры ‘a’ и ‘b’ регулируют вклад значения функции и ее производной на границе, обеспечивая гибкость в определении граничного поведения.

Исследования показали возможность создания систем, демонстрирующих масштабно-инвариантную локализацию, где длина локализации изменяется пропорционально размеру самой системы. Такой режим возникает благодаря точному контролю граничных условий, позволяющему плавно переходить от открытых к периодическим. В отличие от традиционных локализованных состояний, где длина локализации обычно остается фиксированной или изменяется нелинейно, в масштабно-инвариантной локализации увеличение системы приводит к пропорциональному увеличению области, в которой частица удерживается. Это свойство открывает перспективы для создания материалов с предсказуемыми и настраиваемыми транспортными характеристиками, а также для изучения фундаментальных аспектов квантовой механики в нетривиальных условиях. В частности, возможность контролировать длину локализации, не меняя масштаб системы, представляет интерес для разработки новых типов квантовых устройств и сенсоров.

Исследование взаимодействия между граничными условиями и параметрами системы выявило сложное фазовое пространство, демонстрирующее настраиваемые свойства локализации. В этом пространстве, изменение граничных условий — от открытых до периодических — в сочетании с регулировкой параметров системы, позволяет плавно переходить между различными режимами локализации. Наблюдается формирование фаз, характеризующихся как сильной, так и слабой локализацией, а также областей, где локализация полностью отсутствует. Этот контроль над локализацией позволяет создавать системы с предсказуемыми и настраиваемыми свойствами, открывая перспективы для разработки новых материалов и устройств с заданными характеристиками, например, для управления распространением волн или для создания квантовых систем с контролируемой запутанностью. Анализ фазовой диаграммы демонстрирует, что характеристики локализации могут быть тонко настроены, обеспечивая возможность оптимизации системы для конкретных приложений.

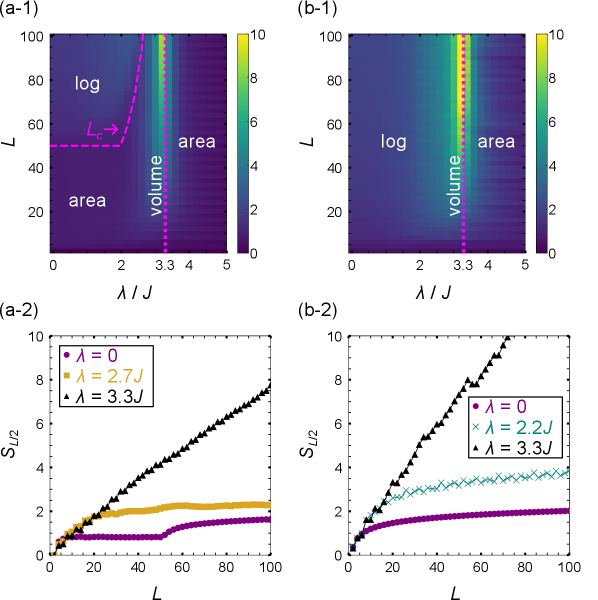
Изучение характеристик безмасштабной локализации становится возможным посредством использования таких мер, как энтропия зацепления, что позволяет выявить лежащие в основе квантовые корреляции. Энтропия зацепления, являясь мерой запутанности между подсистемами, предоставляет информацию о степени связи между различными частями системы, проявляющейся при безмасштабной локализации. Наблюдаемые изменения энтропии зацепления с изменением параметров системы и граничных условий указывают на фундаментальные изменения в структуре квантовых корреляций, подтверждая, что безмасштабная локализация не просто пространственное ограничение, но и проявление сложных квантовых взаимодействий. $S = -Tr(\rho \log \rho)$ — формула, описывающая энтропию зацепления, позволяет количественно оценить эти корреляции и пролить свет на природу безмасштабной локализации в различных физических системах.

Отношение ожидаемой величины скачков на границе к скачкам в объеме системы демонстрирует зависимость от силы квазипериодического потенциала λ, при которой критическое значение <span class="katex-eq" data-katex-display="false">\lambda_c \approx 3.3J</span> определяет переход между режимами. — Отношение ожидаемой величины скачков на границе к скачкам в объеме системы демонстрирует зависимость от силы квазипериодического потенциала λ, при которой критическое значение $\lambda_c \approx 3.3J$ определяет переход между режимами.

Квазипериодичность и локализация: Более глубокая связь

Сочетание квазипериодичности и неэрмитовой физики открывает принципиально новые возможности для изучения явлений локализации. В традиционных периодических системах локализация возникает из-за интерференции волн, приводящей к образованию запрещенных зон. Однако квазипериодические системы, характеризующиеся отсутствием трансляционной симметрии, демонстрируют более сложные сценарии локализации, которые усиливаются при введении неэрмитовых элементов, нарушающих сохранение вероятности. Это приводит к возникновению необычных энергетических спектров и появлению новых типов локализованных состояний, не наблюдаемых в эрмитовых системах. Исследования показывают, что неэрмитовность может существенно изменять критические параметры, определяющие переход от локализованных к расширенным состояниям, и создавать условия для управления локализацией с помощью внешних воздействий. Данный симбиоз позволяет исследовать фундаментальные аспекты волновых процессов и разрабатывать новые материалы с заданными оптическими и электронными свойствами.

Модели, подобные $Aubry-Andre-Harper$ , при объединении с неэрмитовыми элементами демонстрируют уникальные переходы локализации. В то время как традиционные периодические системы предсказывают четкие различия между локализованными и расширенными состояниями, введение квазипериодичности и неэрмитовности приводит к более сложным фазовым переходам. Исследования показывают, что даже небольшие отклонения от эрмитовности могут кардинально изменить характер локализации, приводя к появлению новых типов локализованных состояний и неожиданным зависимостям от параметров системы. Эти переходы не ограничиваются простым переходом от металлических к изолирующим состояниям; они могут включать в себя переходы между различными типами локализации, такими как многократная локализация или локализация, вызванная топологическими дефектами. Понимание этих переходов открывает возможности для проектирования материалов с заданными свойствами.

Возможность управления локализацией посредством граничных условий и параметров системы открывает перспективы для создания материалов с заданными свойствами. Исследования показывают, что, варьируя внешние воздействия на квазипериодическую структуру, можно целенаправленно изменять степень локализации волн внутри материала. Например, изменение граничных условий может приводить к переходу от полностью локализованного состояния к состоянию с расширенными волнами, что напрямую влияет на проводимость, оптические характеристики и другие важные свойства. Такой контроль позволяет конструировать материалы с предсказуемыми и настраиваемыми свойствами, открывая перспективы для разработки новых материалов и устройств с заданными характеристиками, например, для управления распространением волн или для создания квантовых систем с контролируемой запутанностью.

Перспективные исследования направлены на практическое применение принципов квазипериодичности и негермитовности в различных областях. Особое внимание уделяется манипулированию волнами, созданию высокочувствительных сенсоров и разработке систем для квантовой обработки информации. Ключевым моментом в этом направлении является переход, наблюдаемый при силе квазипериодического потенциала около 2.6 $J$ . В этой области происходит подавление “перескоков” на границах системы до формирования связей внутри объема, что открывает возможности для точного контроля и управления локализацией волн и, как следствие, для создания материалов с заданными свойствами и функциональностью.

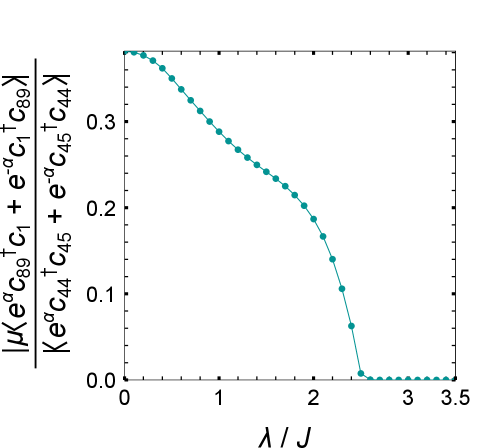
Исследование демонстрирует, что введение квазипериодичности в неэрмитовы системы способно спровоцировать переход от масштабно-инвариантной локализации к режиму, характеризующемуся неэрмитовым эффектом кожи. Этот переход тесно связан с условиями на границах системы и её параметрами. Как отмечал Жан-Поль Сартр: «Существование предшествует сущности». Эта фраза, на первый взгляд, далека от физики, но отражает суть происходящего: система проявляет определенные свойства — локализацию или эффект кожи — в зависимости от тех условий, в которых она оказывается. Иными словами, конкретная конфигурация системы определяет её поведение, а не некая заранее заданная сущность. Исследование показывает, что графики, описывающие эти переходы, — это не просто математические абстракции, а психограммы эпохи, отражающие нашу потребность в упорядочивании и предсказуемости в сложных системах.

Что дальше?

Представленная работа демонстрирует, как тонкое нарушение порядка в квазипериодических неэрмитовых системах может привести к радикальным изменениям в локализации. Однако, следует признать, что само понятие «локализации» в таких системах требует более глубокого осмысления. Ведь даже при идеальном знании параметров, система склонна выбирать то состояние, которое подтверждает уже существующие представления о себе — в данном случае, склонность к тому или иному режиму. Особенно важно понимать, что большинство «решений» системы — это не стремление к выгоде, а попытка избежать сожаления о неправильном выборе.

Перспективы дальнейших исследований лежат в изучении влияния различных типов неупорядоченности на наблюдаемый эффект. Насколько устойчивы полученные результаты к добавлению случайных потенциалов или к изменениям геометрии системы? Более того, необходимо разработать более адекватные методы для характеристики локализации в неэрмитовых системах, учитывающие не только спектральные свойства, но и энтропийные характеристики волновых функций. Игнорирование этих аспектов — это всё равно что пытаться понять море, изучая лишь его поверхность.

В конечном счёте, исследование неэрмитовых систем — это не просто поиск новых физических эффектов, а попытка понять, как порядок возникает из хаоса, и как даже самые сложные системы подчиняются простым, но часто неочевидным правилам. И, возможно, это понимание поможет объяснить не только поведение электронов в кристаллах, но и поведение людей на рынках.

Оригинал статьи: https://arxiv.org/pdf/2602.11155.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-13 03:36