Квантовый газ в ловушке: новые грани дальних взаимодействий

Автор: Денис Аветисян

Исследование методом квантоваго Монте-Карло раскрывает сложные фазовые переходы и свойства одномерного квантового газа, взаимодействующего посредством посредничества оптической полости.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал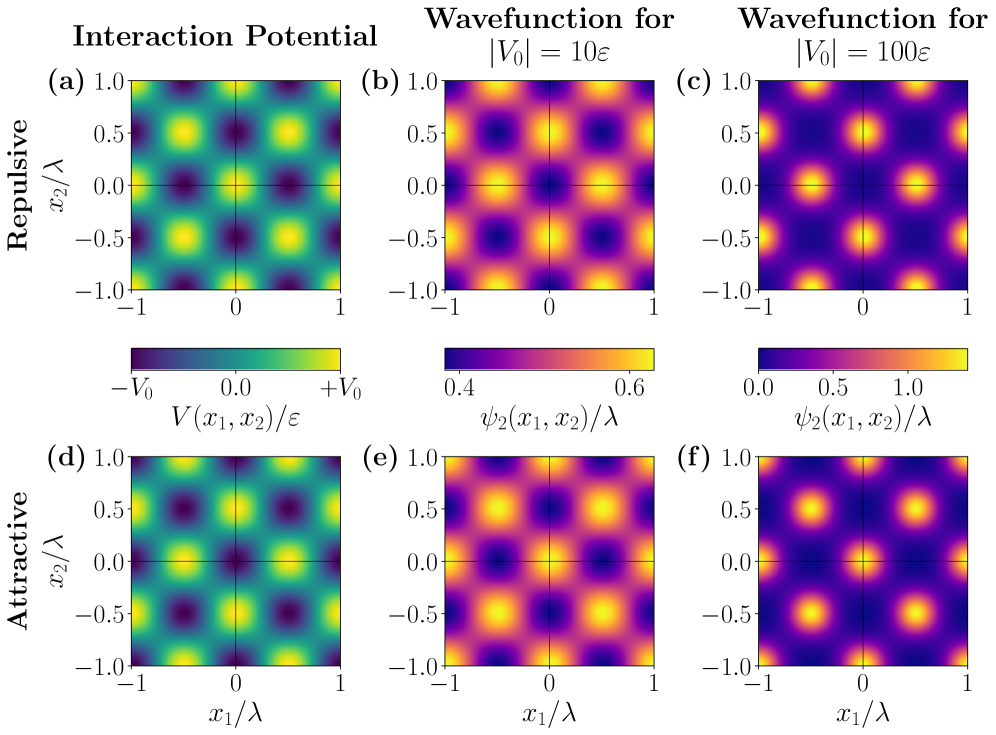

В рамках исследования взаимодействия частиц, потенциал дальнодействия, обусловленный полостью, проявляется в различных формах в зависимости от силы взаимодействия <span class="katex-eq" data-katex-display="false">V_0</span>, что находит отражение в волновых функциях основного состояния <span class="katex-eq" data-katex-display="false">\psi(x_1, x_2)</span>, демонстрирующих различные конфигурации для отталкивающих и притягивающих взаимодействий. — В рамках исследования взаимодействия частиц, потенциал дальнодействия, обусловленный полостью, проявляется в различных формах в зависимости от силы взаимодействия $V_0$ , что находит отражение в волновых функциях основного состояния $\psi(x_1, x_2)$ , демонстрирующих различные конфигурации для отталкивающих и притягивающих взаимодействий.

Работа посвящена изучению основного состояния квантовой системы с дальними взаимодействиями, опосредованными полостью, и выявлению делокализованных связанных состояний и мезоскопических газовых фаз.

Исследование квантовых систем с дальними взаимодействиями представляет собой сложную задачу, требующую разработки эффективных вычислительных методов. В работе «Quantum Monte Carlo study of systems interacting via long-range interactions mediated by a cavity» представлено детальное изучение одномерных квантовых газов с взаимодействиями бесконечного радиуса действия, опосредованными оптической полостью, с использованием вариационных и диффузионных методов Монте-Карло. Полученные результаты демонстрируют богатое фазовое пространство, включающее делокализованные связанные состояния и мезоскопические газовые фазы, зависящие от квантовой статистики и силы взаимодействий. Какие новые перспективы открывает исследование подобных систем для понимания коллективных явлений в конденсированном веществе и разработки новых квантовых технологий?

Дальнодействие: Преодолевая Границы Моделирования

Традиционно, задачи многочастичной физики сталкиваются с существенными трудностями в управлении дальнодействующими взаимодействиями между частицами. Это ограничение существенно препятствует исследованию новых фаз материи, поскольку точное моделирование систем, где влияние одной частицы распространяется на удаленные, требует огромных вычислительных ресурсов и часто приводит к неточностям. В то время как ближние взаимодействия относительно легко контролировать и описывать, дальнодействующие силы вносят сложность, требующую инновационных подходов к проектированию экспериментов и разработке теоретических моделей. Именно эта сложность долгое время сдерживала прогресс в понимании экзотических состояний материи и исследовании фундаментальных физических явлений, требующих точного контроля над взаимодействиями на больших расстояниях.

Традиционные методы моделирования, как правило, испытывают затруднения при работе с системами, где взаимодействие между частицами не ограничивается ближайшими соседями. Это связано с тем, что большинство алгоритмов и приближений оптимизированы для локальных взаимодействий, и их применение к системам с дальнодействующими связями приводит к существенным погрешностям в предсказаниях. В результате, понимание новых, возникающих явлений, таких как экзотические фазы материи или сложные коллективные поведения, остаётся неполным. Неспособность точно учесть дальнодействие ограничивает возможности предсказать свойства систем и контролировать их, что препятствует как фундаментальным исследованиям, так и разработке новых материалов и технологий.

Точный контроль над взаимодействиями между частицами представляется ключевым для создания и наблюдения экзотических состояний материи, таких как сверхтекучесть. Исследования в этой области направлены не только на подтверждение теоретических предсказаний, но и на изучение неравновесных фазовых переходов, где системы не находятся в состоянии термодинамического равновесия. Подобный контроль позволяет выйти за рамки традиционных моделей и исследовать так называемую «фрустрированную мезоскопическую фазу» — состояние, характеризующееся сложной структурой и нетривиальными свойствами, возникающими вследствие конкурирующих взаимодействий между частицами на мезоскопическом уровне. Развитие методов управления этими взаимодействиями открывает перспективы для создания новых материалов с уникальными свойствами и углубленного понимания фундаментальных законов физики конденсированного состояния.

Моделирование спин-независимой фермионной системы из 5 частиц с притягивающими взаимодействиями, опосредованными полостью, демонстрирует изменение плотности профиля и двухчастичной корреляционной функции в зависимости от силы взаимодействия <span class="katex-eq" data-katex-display="false">V_0</span>, переход к периодической структуре при сильном взаимодействии, а также изменение энергии на частицу и фракции сверхтекучести, определяемой границей Леггета (уравнение (16)). — Моделирование спин-независимой фермионной системы из 5 частиц с притягивающими взаимодействиями, опосредованными полостью, демонстрирует изменение плотности профиля и двухчастичной корреляционной функции в зависимости от силы взаимодействия $V_0$ , переход к периодической структуре при сильном взаимодействии, а также изменение энергии на частицу и фракции сверхтекучести, определяемой границей Леггета (уравнение (16)).

Инструменты для Дальнего Взаимодействия: Новые Платформы

Высокорезонансные оптические резонаторы и мультимодовые резонаторы представляют собой универсальные платформы для реализации дальнодействующих взаимодействий, опосредованных фотонами. В данных резонаторах свет многократно отражается между зеркалами, значительно увеличивая вероятность взаимодействия между частицами, расположенными на расстоянии. Эффективный радиус взаимодействия определяется длиной волны света и размерами резонатора, что позволяет преодолеть ограничения, связанные с прямыми взаимодействиями на больших расстояниях. Использование высокорезонансных резонаторов позволяет достичь эффективного увеличения силы взаимодействия между частицами, что критически важно для изучения многих телесных систем и реализации новых квантовых эффектов. Регулируя параметры резонатора, такие как частота и моды, можно точно настраивать дальность и силу этих дальнодействующих взаимодействий.

Динамически настраиваемые оптические решетки и программируемые оптомеханические массивы обеспечивают точный контроль над силой и конфигурацией взаимодействий между частицами. Использование цифровой микрозеркальной технологии (DMD) и акустооптических модуляторов (AOM) позволяет формировать произвольные потенциальные ландшафты для атомов и фотонов, варьируя глубину потенциальных ям и расстояние между ними. Это дает возможность создавать как однородные, так и неоднородные системы с заданными параметрами взаимодействия, необходимые для изучения многочастичных систем и реализации специфических квантовых состояний. Такой подход позволяет исследовать влияние различных конфигураций взаимодействия на коллективное поведение частиц, моделируя широкий спектр физических систем, от конденсированных сред до квантовых симуляторов.

Использование высокоточных оптических резонаторов и программируемых оптомеханических массивов позволяет создавать эффективные взаимодействия бесконечной дальности между частицами в квантовых газах. Это приводит к существенному изменению их коллективного поведения, поскольку корреляции между частицами не ограничены расстоянием. В результате, наблюдается формирование фрустрированной мезоскопической фазы, характеризующейся отсутствием глобального упорядочения и появлением локальных, конкурирующих взаимодействий, что открывает возможности для изучения новых типов квантовых состояний материи и проверки теоретических моделей, описывающих сложные многочастичные системы. Такие системы демонстрируют свойства, не наблюдаемые в традиционных квантовых газах с взаимодействиями короткой дальности.

Результаты вариационного Монте-Карло показывают, что энергия основного состояния бозонов, взаимодействующих посредством дальнодействующего потенциала, зависит от силы взаимодействия: при положительных значениях <span class="katex-eq" data-katex-display="false">V_0</span> энергия стремится к определенному пределу при увеличении числа частиц, а при отрицательных - расходится, демонстрируя соответствие асимптотическому закону масштабирования для отталкивающего взаимодействия и расходимость для притягивающего. — Результаты вариационного Монте-Карло показывают, что энергия основного состояния бозонов, взаимодействующих посредством дальнодействующего потенциала, зависит от силы взаимодействия: при положительных значениях $V_0$ энергия стремится к определенному пределу при увеличении числа частиц, а при отрицательных — расходится, демонстрируя соответствие асимптотическому закону масштабирования для отталкивающего взаимодействия и расходимость для притягивающего.

Теория и Эксперимент: Подтверждение Моделей

Расширенная модель Бозе-Хаббарда (Extended Bose-Hubbard Model) представляет собой теоретическую основу для исследования поведения бозе-газов в оптических решетках, учитывающую дальнодействующие взаимодействия. В отличие от традиционной модели Бозе-Хаббарда, которая рассматривает только взаимодействия ближайших соседей, расширенная модель включает в себя члены, описывающие взаимодействия между частицами на больших расстояниях. Это позволяет более точно моделировать системы, в которых дальнодействующие взаимодействия играют значительную роль, например, газы, удерживаемые в оптических ловушках с определенной геометрией. Математически, расширенная модель включает дополнительные члены в гамильтониан, описывающие потенциал взаимодействия между частицами, зависящий от расстояния между ними. Это приводит к изменению фазовой диаграммы системы и появлению новых фаз, не наблюдаемых в традиционной модели. $H = -J \sum_{\langle i,j \rangle} (b_i^\dagger b_j + b_j^\dagger b_i) + \frac{U}{2} \sum_i n_i (n_i - 1) + V \sum_{i,j} \frac{1}{|r_i - r_j|} n_i n_j$ , где J — параметр туннелирования, U — сила локального отталкивания, V — сила дальнодействующего взаимодействия, а $n_i$ — оператор числа частиц на сайте i.

Методы вариационного Монте-Карло (VMC) и диффузионного Монте-Карло (DMC) позволяют проводить точные вычисления свойств основного состояния квантовых систем. VMC использует пробные волновые функции, параметры которых оптимизируются для минимизации энергии, предоставляя приближенное решение. DMC, в свою очередь, основан на эволюции волновой функции во мнимом времени, что приводит к проекции на основное состояние и более точным результатам. Оба метода эффективно применяются для анализа систем с многочастичными взаимодействиями, где аналитическое решение невозможно, и служат для верификации теоретических предсказаний путем сравнения с результатами численного моделирования и, в конечном итоге, с экспериментальными данными. $\Psi(\mathbf{r})$ — пример волновой функции, используемой в этих расчетах.

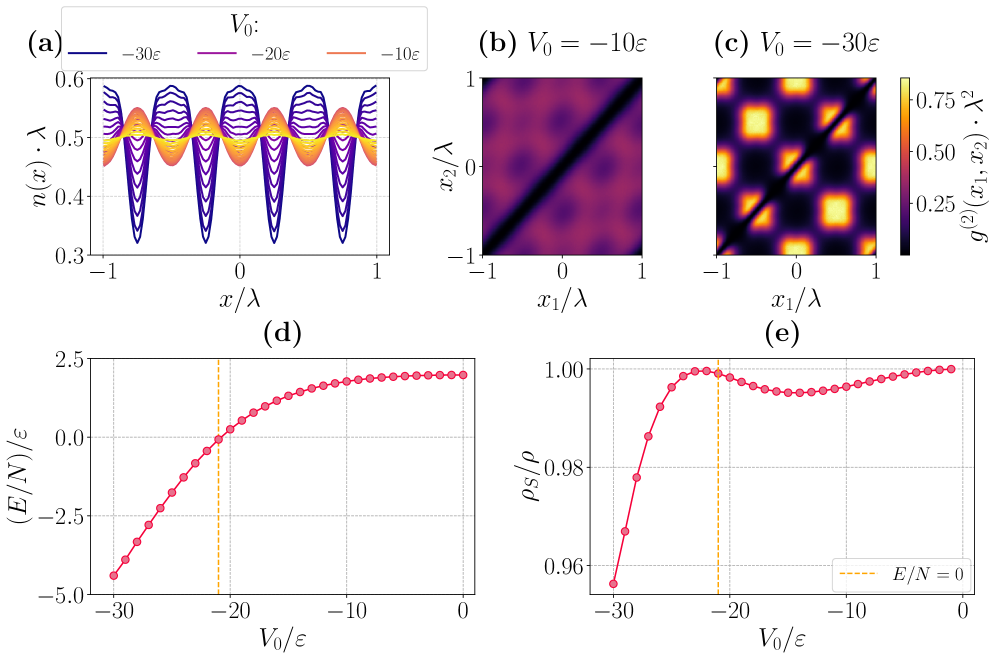
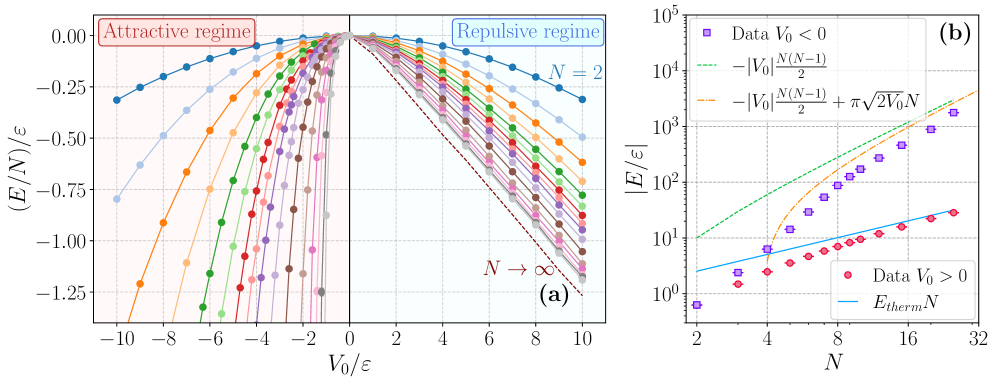
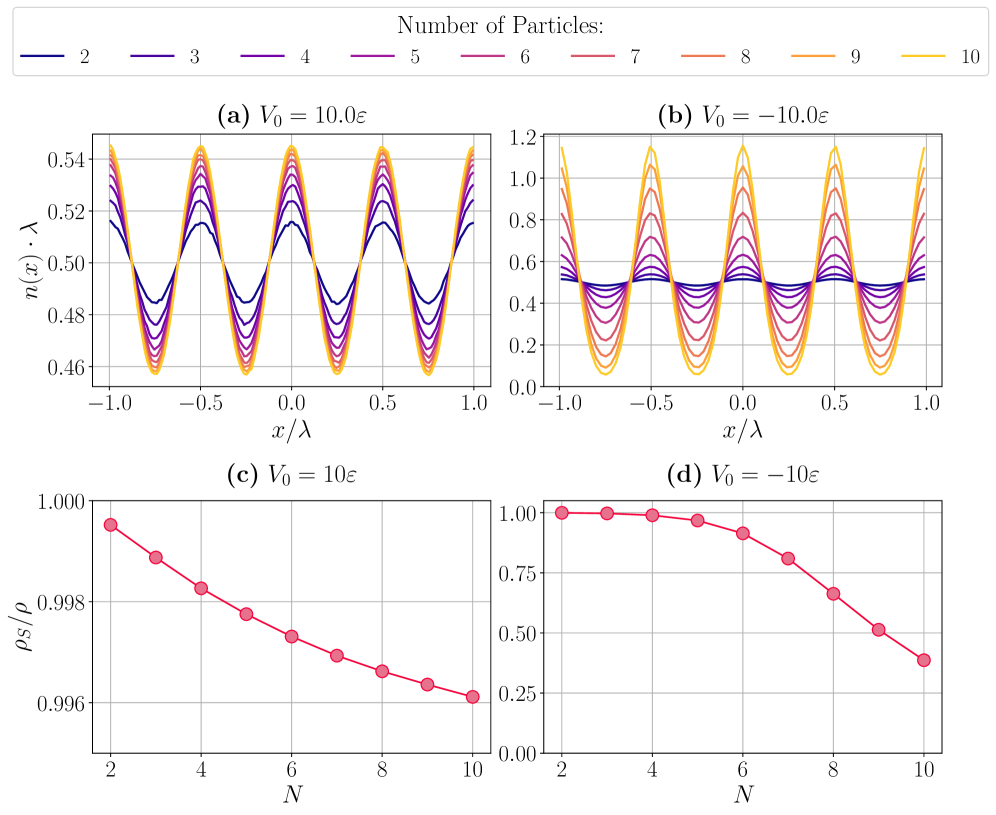
Анализ наблюдаемых характеристик одномерных квантовых газов, таких как статический фактор структуры, профиль плотности и функция парных распределений, позволяет непосредственно исследовать влияние дальнодействующих взаимодействий. Эти измерения позволяют подтвердить адекватность теоретических моделей и выявить точки перехода между различными фазами вещества. В частности, установлено, что при изменении параметров системы происходит переход от мезоскопического газа к фрустрированной фазе и, далее, к делокализованному связанному состоянию. Количественная оценка этих наблюдаемых предоставляет данные для верификации численных методов и уточнения теоретических предсказаний относительно поведения бозе-газов в оптических решетках.

Сравнение энергий, полученных методом вариационного Монте-Карло (<span class="katex-eq" data-katex-display="false"> ext{VMC}</span>) и диффузионного Монте-Карло (<span class="katex-eq" data-katex-display="false"> ext{DMC}</span>) с использованием одинаковой пробной волновой функции, показывает, что <span class="katex-eq" data-katex-display="false"> ext{DMC}</span> обеспечивает более точные результаты как для систем с дальним взаимодействием, так и для систем с комбинированным контактным и дальним взаимодействием, а также для фермионных систем. — Сравнение энергий, полученных методом вариационного Монте-Карло ( $ext{VMC}$ ) и диффузионного Монте-Карло ( $ext{DMC}$ ) с использованием одинаковой пробной волновой функции, показывает, что $ext{DMC}$ обеспечивает более точные результаты как для систем с дальним взаимодействием, так и для систем с комбинированным контактным и дальним взаимодействием, а также для фермионных систем.

Развитие Новых Фаз: Сверхтекучесть и За Её Пределами

Исследования показали, что взаимодействия на больших расстояниях играют ключевую роль в стабилизации сверхтекучести, уникального состояния вещества, сочетающего в себе свойства сверхтекучести и дальнего порядка. В этом состоянии частицы могут течь без вязкости, одновременно формируя упорядоченную кристаллическую структуру. В отличие от обычных кристаллов, где атомы фиксированы в определенных положениях, в сверхтекучем кристалле атомы могут перемещаться, сохраняя при этом общую упорядоченность. Эти взаимодействия способствуют возникновению и поддержанию этой сложной структуры, обеспечивая стабильность сверхтекучего состояния даже при относительно высоких температурах. Наблюдаемый дальний порядок, характеризующийся упорядоченным расположением атомов на больших расстояниях, является прямым следствием этих взаимодействий и отличает сверхтекучий кристалл от обычных твердых тел.

Исследования показывают, что взаимодействие между частицами способно вызывать фазовые переходы, протекающие вне состояния равновесия. В отличие от классических фазовых переходов, где система стремится к минимальной энергии, неравновесные переходы приводят к возникновению экзотических состояний материи, недоступных в обычных условиях. Эти состояния характеризуются уникальными свойствами и поведением, такими как самоорганизация, флуктуации и нелинейные эффекты. Подобные переходы позволяют создавать новые материалы с заданными характеристиками и открывают перспективы для разработки принципиально новых технологий, использующих необычные свойства материи, существующей лишь вдали от равновесия.

Возможность точного контроля над взаимодействиями между частицами открывает перед исследователями беспрецедентные перспективы в создании и манипулировании новыми фазами материи. Данный контроль позволяет не только стабилизировать экзотические состояния, такие как сверхтекучесть с дальним порядком, но и активно управлять их свойствами. Важно отметить, что перед переходом в делокализованное связанное состояние, наблюдается конечная сверхтекучая фракция, что указывает на уникальные возможности для создания устройств с нулевым трением и высокой эффективностью. Перспективные области применения включают создание сверхчувствительных сенсоров, квантовых компьютеров и принципиально новых материалов с заданными свойствами, а также разработку технологий хранения и передачи энергии без потерь.

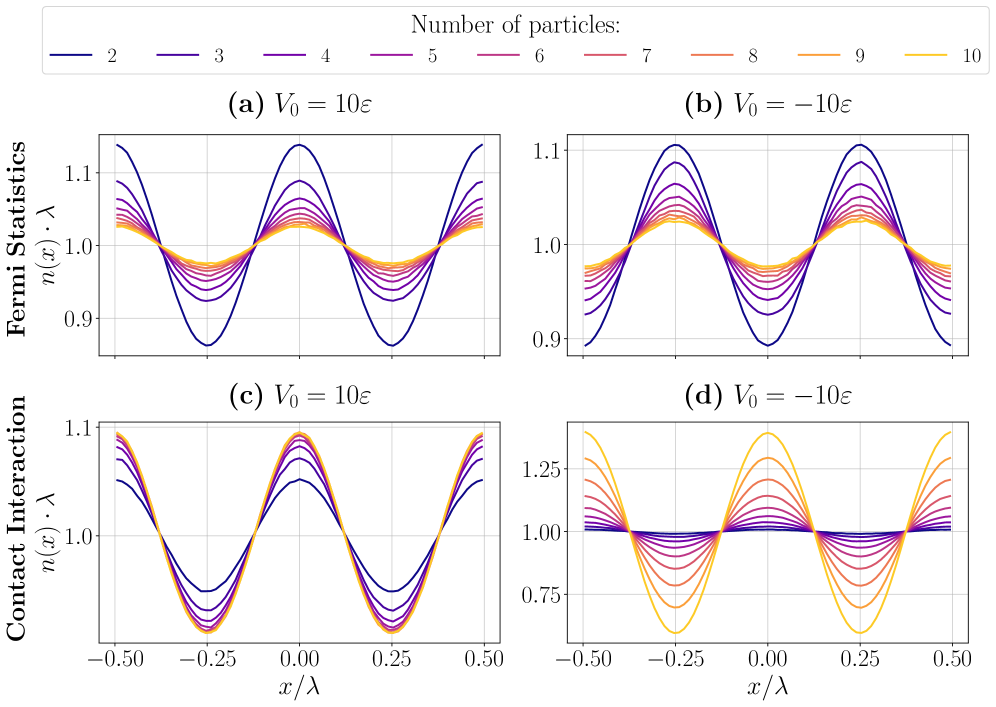
Результаты моделирования методом Монте-Карло показали, что увеличение числа частиц <span class="katex-eq" data-katex-display="false">N</span> приводит к росту амплитуды профиля плотности <span class="katex-eq" data-katex-display="false">n(x)</span> и, как следствие, к увеличению доли сверхтекучей фракции <span class="katex-eq" data-katex-display="false">ρ_s/ρ</span>, что наблюдается как для отталкивающих (<span class="katex-eq" data-katex-display="false">V_0 > 0</span>), так и для притягивающих (<span class="katex-eq" data-katex-display="false">V_0 < 0</span>) взаимодействий при фиксированной длине системы <span class="katex-eq" data-katex-display="false">L = 2λ</span> и изменяющейся плотности <span class="katex-eq" data-katex-display="false">ρ = N/L</span>. — Результаты моделирования методом Монте-Карло показали, что увеличение числа частиц $N$ приводит к росту амплитуды профиля плотности $n(x)$ и, как следствие, к увеличению доли сверхтекучей фракции $ρ_s/ρ$ , что наблюдается как для отталкивающих ( $V_0 > 0$ ), так и для притягивающих ( $V_0 < 0$ ) взаимодействий при фиксированной длине системы $L = 2λ$ и изменяющейся плотности $ρ = N/L$ .

Роль Статистики: Фермионы и За Её Пределами

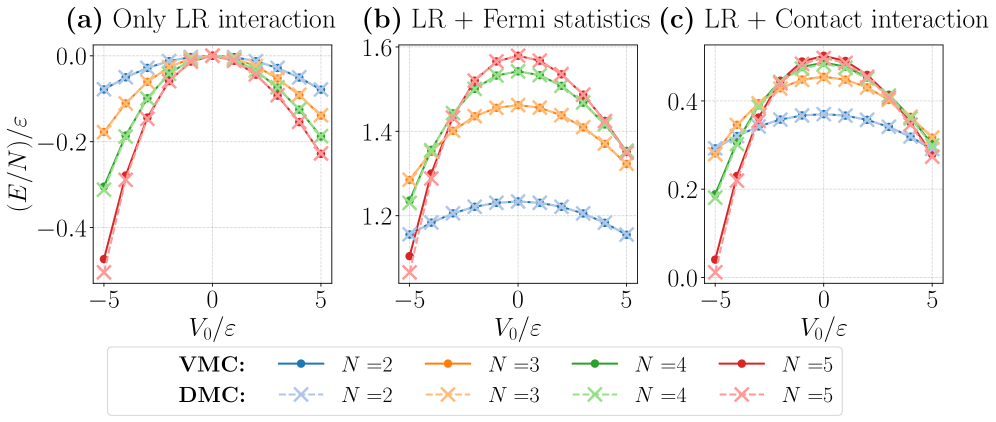
Для фермионных систем учет влияния статистики Ферми является фундаментальным. Вследствие принципа Паули, описывающего антисимметричность волновой функции, стандартные методы, используемые для бозонных систем, оказываются неприменимыми. Для получения точных результатов в таких случаях, как правило, применяются вычислительные подходы, такие как метод Монте-Карло, включающий приближение с фиксированной узловой линией. Данное приближение позволяет контролировать знак волновой функции и, таким образом, преодолеть проблему “знаковой проблемы”, возникающую при моделировании фермионных систем. Точность расчетов напрямую зависит от качества пробной волновой функции и, следовательно, от понимания корреляционных эффектов между фермионами, что делает разработку эффективных приближений ключевой задачей в этой области.

Исследование систем, населённых частицами с различными статистическими свойствами — от фермионов и бозонов до более экзотических случаев — позволяет углубить понимание фундаментальной связи между взаимодействиями, статистикой и возникающими явлениями. Изменяя статистические характеристики частиц, учёные могут искусственно влиять на коллективное поведение материи, приводя к появлению новых фаз и свойств, которые невозможно наблюдать в обычных условиях. Например, изучение систем с промежуточной статистикой, отличной от привычной ферми-дираковской или бозе-эйнштейновской, открывает перспективы для создания материалов с уникальными квантовыми свойствами. Такие исследования не только расширяют теоретические представления о природе материи, но и могут привести к разработке принципиально новых технологий в области квантовых вычислений и материаловедения.

Будущие исследования направлены на расширение применимости существующих методов к системам с более сложной структурой, что позволит изучать и, возможно, контролировать экзотические фазы материи, ранее недоступные для наблюдения. Особое внимание уделяется проверке качества исходных волновых функций, используемых в вычислительных подходах. Значительные расхождения между результатами, полученными методами вариационного Монте-Карло $VMC$ и диффузионного Монте-Карло $DMC$ , свидетельствуют о наличии сложных корреляций между частицами, требующих более точного описания и, следовательно, разработки усовершенствованных алгоритмов и аппроксимаций. Такой подход не только углубит понимание фундаментальных свойств материи, но и откроет перспективы для создания новых материалов с уникальными характеристиками.

Метод Монте-Карло показал, что плотность частиц <span class="katex-eq" data-katex-display="false">n(x)</span> и доля сверхтекучей фракции <span class="katex-eq" data-katex-display="false">ρ_s/ρ</span> увеличиваются с ростом их числа (от 2 до 10) как для отталкивающих (<span class="katex-eq" data-katex-display="false">V_0 > 0</span>), так и для притягивающих (<span class="katex-eq" data-katex-display="false">V_0 < 0</span>) взаимодействий при фиксированной длине системы <span class="katex-eq" data-katex-display="false">L = 2λ</span> и плотности <span class="katex-eq" data-katex-display="false">ρ = N/L</span>. — Метод Монте-Карло показал, что плотность частиц $n(x)$ и доля сверхтекучей фракции $ρ_s/ρ$ увеличиваются с ростом их числа (от 2 до 10) как для отталкивающих ( $V_0 > 0$ ), так и для притягивающих ( $V_0 < 0$ ) взаимодействий при фиксированной длине системы $L = 2λ$ и плотности $ρ = N/L$ .

Исследование, представленное в данной работе, демонстрирует хрупкость любого теоретического построения перед лицом сложной квантовой системы. Подобно тому, как горизонт событий поглощает информацию, так и кажущаяся надёжность методов квантовского моделирования может оказаться иллюзией при рассмотрении систем с дальнодействующими взаимодействиями. Иммануил Кант некогда заметил: «Все наши познания начинаются с чувств, но завершаются в разуме». В контексте этой работы, стремление к познанию свойств бозе-эйнштейновского конденсата с дальнодействующими связями требует не только точных расчётов, но и осознания границ применимости используемых методов, ведь любое «закон», как и любое теоретическое описание, может раствориться в горизонте событий неполного знания.

Что же дальше?

Представленная работа, как и любая попытка описать квантовую материю, лишь приоткрывает завесу над бесконечной сложностью взаимодействий. Расчёты, пусть и демонстрирующие богатство фазовой диаграммы одномерных систем с дальнодействующими связями, остаются приближением, тенью истинного состояния. Каждый найденный «делокализованный связанный» состояние — это не триумф понимания, а лишь констатация границ применимости используемых методов. Подобно попытке удержать свет в ладони, любое численное решение неминуемо теряет точность, приближаясь к горизонту событий, где наши представления о реальности рушатся.

Будущие исследования неизбежно столкнутся с необходимостью преодоления ограничений используемых приближений. Развитие алгоритмов квантовского Монте-Карло, способных учитывать более сложные корреляции и эффекты статистик частиц, представляется критически важным. Однако, даже самые совершенные численные методы не смогут дать окончательный ответ. Истинное понимание, вероятно, лежит за пределами возможностей вычислений, в области новых теоретических концепций, способных объединить квантовую механику и гравитацию.

Можно ли будет создать систему, в которой дальнодействующие взаимодействия полностью контролируются, позволяя изучать квантовые фазы материи с беспрецедентной точностью? Этот вопрос, вероятно, останется открытым надолго. Ведь любое вмешательство в квантовый мир неизбежно вносит возмущения, искажая картину. Кажется, что полное понимание — это мираж, к которому можно приближаться бесконечно, но никогда не достичь.

Оригинал статьи: https://arxiv.org/pdf/2601.10301.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-16 19:08