Автор: Денис Аветисян
Новое исследование раскрывает механизмы, лежащие в основе ускоренной релаксации в открытых квантовых системах, известной как квантовый эффект Мпембы.
Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.
Бесплатный телеграм-канал
Исследование посвящено изучению квантового эффекта Мпембы в открытых квантовых системах с использованием марковских динамических моделей и декогерентно-свободных подпространств.
Несмотря на кажущуюся простоту термодинамики, феномен ускоренного достижения равновесия в определенных системах продолжает вызывать научный интерес. В работе, посвященной исследованию ‘Unraveling the Quantum Mpemba Effect on Markovian Open Quantum Systems’, авторы анализируют квантовый аналог эффекта Мпембы в открытых квантовых системах. Показано, что использование декогерентно-свободных подпространств и манипулирование начальными состояниями может приводить к экспоненциальному ускорению релаксации к равновесию. Какие новые горизонты открывает понимание этого неинтуитивного явления для разработки когерентных квантовых технологий и управления открытыми квантовыми системами?
Эффект Мпембы: Парадокс, Бросающий Вызов Интуиции
Эффект Мпембы представляет собой контринтуитивное явление, когда более горячая система в определенных условиях может остывать быстрее, чем более холодная, что противоречит классическим представлениям термодинамики. Этот парадокс, впервые отмеченный учеником школы Мпембой в Танзании, заключается в том, что горячий лёд иногда замерзает быстрее, чем холодный, несмотря на необходимость отдать больше тепла для достижения точки замерзания. Изначально воспринимаемый как аномалия, эффект Мпембы стимулировал обширные исследования, направленные на выявление физических механизмов, лежащих в основе этого поведения. Предлагаемые объяснения включают конвекцию, переохлаждение, образование льда и растворенные газы, но единого общепринятого объяснения до сих пор не существует, что делает эффект Мпембы предметом продолжающихся научных дискуссий и экспериментов.
Неожиданное поведение, известное как эффект Мпемба, когда более горячая система может остывать быстрее, чем более холодная, вызвало широкий интерес и междисциплинарные исследования. Изначально замеченное в контексте замораживания воды, это явление привлекло внимание физиков, стремящихся понять его термодинамические основы, и химиков, исследующих роль растворенных газов и конвекции. Исследователи из области материаловедения изучают, как свойства материалов влияют на скорость теплоотдачи, а специалисты по нелинейной динамике пытаются смоделировать и предсказать подобные парадоксальные процессы. В результате этих усилий были предложены различные гипотезы, включая роль переохлаждения, испарения и неравномерного распределения тепла, хотя единого, общепринятого объяснения до сих пор не существует. Интенсивные исследования в этой области продолжаются, что подчеркивает важность эффекта Мпембы как стимула для углубления понимания фундаментальных принципов теплопередачи и термодинамики.
Перенос эффекта Мпембы в квантовую область открывает совершенно новые горизонты и одновременно ставит перед учеными серьезные теоретические задачи. В то время как классическое понимание этого феномена связано с параметрами макроскопических систем, таких как конвекция и переохлаждение, квантовые аналоги требуют учета эффектов суперпозиции, запутанности и квантовой когерентности. Исследование охлаждения квантовых систем, например, кубитов или квантовых конденсатов, может привести к разработке принципиально новых методов управления квантовой информацией и повышения эффективности квантовых технологий. Однако, для адекватного описания этих процессов необходимы новые математические модели и подходы, выходящие за рамки классической термодинамики и требующие применения методов квантовой механики и теории открытых квантовых систем. Например, учет влияния квантовых флуктуаций и декогеренции может существенно изменить характер охлаждения, приводя к неинтуитивным результатам и требуя разработки новых теоретических инструментов для предсказания и контроля этих процессов.
Марковский Подход: Ключ к Пониманию Квантового Охлаждения
Эффект квантового Мпембы, демонстрирующий аномальную скорость охлаждения некоторых квантовых систем, наиболее адекватно объясняется в рамках теории марковских открытых квантовых систем. Данный подход предполагает, что взаимодействие системы с окружающей средой является случайным и не имеет «памяти» о предыдущих состояниях. Это позволяет упростить математическое описание динамики системы, рассматривая только текущее состояние и вероятности перехода между состояниями. В отличие от немарковских моделей, учитывающих когерентные обратные влияния среды, марковский подход фокусируется на диссипативных процессах, что позволяет эффективно моделировать эффекты, возникающие из-за потери энергии в окружающую среду и дефазировки квантовых состояний. Именно этот подход позволяет выявить и объяснить условия, при которых наблюдается ускоренное охлаждение, связывая его с особенностями взаимодействия системы и среды, а также с начальными условиями системы.
Уравнение Линдблада представляет собой мощный математический аппарат для описания эволюции во времени открытых квантовых систем, взаимодействующих с окружающей средой. Оно описывает изменение матрицы плотности $\rho$ во времени как: $\frac{d\rho}{dt} = -\frac{i}{\hbar}[H, \rho] + \mathcal{L}[\rho]$, где $H$ — гамильтониан системы, а $\mathcal{L}[\rho]$ — лиувилевский супероператор, учитывающий влияние окружающей среды через диссипативные и шумовые процессы. Этот супероператор обеспечивает сохранение следа матрицы плотности и положительную определенность, что соответствует физическим требованиям к квантовым состояниям. Уравнение Линдблада позволяет моделировать различные явления, такие как спонтанное излучение, дефазировка и диссипация энергии, возникающие вследствие взаимодействия системы с окружающей средой, и является ключевым инструментом в квантовой оптике и физике открытых систем.
В основе формализма открытых квантовых систем лежит супероператор Лиувилля, определяющий динамику матрицы плотности $\rho(t)$. Этот супероператор, действуя на оператор плотности, описывает изменение состояния системы во времени под воздействием окружающей среды. Математически, эволюция матрицы плотности задается уравнением Линдблада: $\frac{d\rho}{dt} = -i\mathcal{L}\rho$, где $\mathcal{L}$ — супероператор Лиувилля. Его структура включает гамильтониан системы и члены, описывающие диссипацию и декогеренцию, вызванные взаимодействием с окружением. Таким образом, супероператор Лиувилля обеспечивает формальное описание не только унитарной эволюции, но и неермитовской динамики, обусловленной влиянием внешней среды.
Состояния и Динамика: Квантовые Отпечатки Эффекта Мпембы
Для наблюдения квантического эффекта Мпембы, заключающегося в ускоренном охлаждении горячей системы по сравнению с холодной, критически важен выбор начального состояния квантовой системы. Состояния, такие как когерентные состояния ($|\alpha\rangle$) и выжатые вакуумные состояния ($|r, \theta\rangle$), обладают специфическими свойствами, влияющими на динамику теплообмена. Когерентные состояния характеризуются определенной амплитудой и фазой, а выжатые состояния демонстрируют уменьшение квантовых флуктуаций в одной из квадратур электромагнитного поля, что влияет на скорость релаксации к тепловому равновесию. Экспериментальные и теоретические исследования показывают, что именно использование данных состояний в качестве начальных условий позволяет проявить и изучить квантический аналог эффекта Мпембы, отличающийся от классического поведения.
Представление системы как бозонной гауссовой системы, характеризуемой формализмом ковариационной матрицы, значительно упрощает анализ динамики квантопембовского эффекта. В рамках этого подхода, операторы, описывающие систему, подчиняются гауссовым распределениям, что позволяет полностью охарактеризовать состояние системы с помощью первого и второго моментов этих операторов. Ковариационная матрица $V$ определяет дисперсии и корреляции между квадратурами бозонных операторов, обеспечивая компактное представление состояния. Использование формализма ковариационной матрицы позволяет аналитически отслеживать эволюцию системы во времени, избегая необходимости работы с полными матрицами плотности и значительно сокращая вычислительную сложность, особенно в случае большого числа частиц.
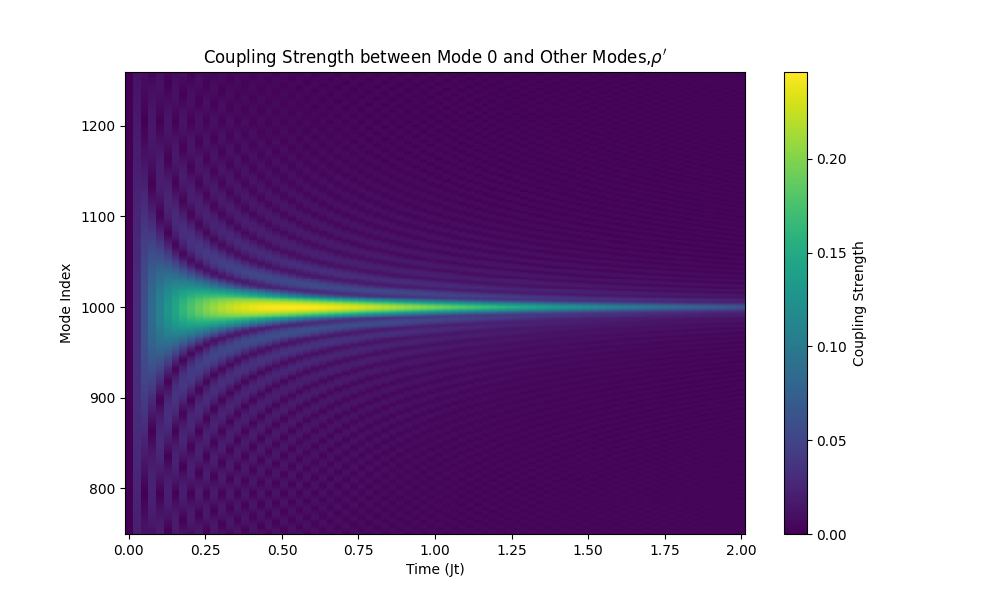
Карта Дэвиса представляет собой специфический подход к описанию динамики открытых квантовых систем, расширяющий рамки марковского приближения. В отличие от стандартных марковских процессов, предполагающих отсутствие памяти о начальном состоянии системы, карта Дэвиса позволяет учитывать немарковские эффекты, возникающие из-за взаимодействия системы с окружающей средой. Математически, карта Дэвиса определяется как суперпозиция операторов, соответствующих различным траекториям стохастического процесса, описывающего влияние среды. Она выражается через $ \mathcal{D}[\Phi] \rho = \sum_k E_k \rho E_k^\dagger $, где $E_k$ — операторы Крауса, зависящие от свойств резервуара и времени эволюции. Использование карты Дэвиса позволяет моделировать системы, в которых корреляции в окружающей среде сохраняются достаточно долго, чтобы влиять на динамику квантовой системы.
Количественная Оценка: Метрики, Подтверждающие Эффект
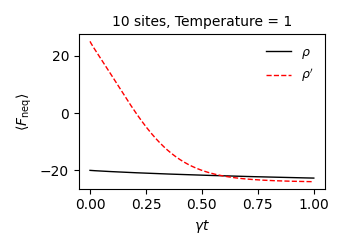
Свободная энергия неравновесного состояния выступает ключевым показателем, позволяющим количественно оценить отклонение системы от теплового равновесия. Этот параметр играет решающую роль в выявлении условий, при которых наблюдается квантический эффект Мпембы — парадоксальное явление, когда горячая система охлаждается быстрее холодной. Исследование показывает, что величина свободной энергии напрямую связана со скоростью релаксации системы, и именно значительное отклонение от равновесия создает благоприятную среду для ускоренного охлаждения. Анализ свободной энергии позволяет не только подтвердить существование эффекта, но и предсказать его проявление в различных физических системах, открывая перспективы для управления тепловыми процессами на квантовом уровне. В частности, установлено, что чем больше система удалена от равновесия, тем сильнее выражен эффект Мпембы, что подтверждается расчетами и экспериментальными данными.
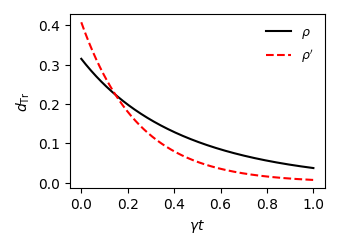
Для количественной оценки различий между траекториями охлаждения используется понятие “Расстояния Трассировки” (Trace Distance), которое измеряет степень несхожести между матрицами плотности, описывающими состояние системы в различные моменты времени. Данный показатель позволяет не только определить, насколько сильно отличаются процессы охлаждения при различных условиях, но и установить количественную меру различий между скоростями охлаждения. Чем больше расстояние трассировки между двумя матрицами плотности, тем более различны соответствующие состояния системы и, следовательно, траектории охлаждения. Таким образом, $Trace Distance$ выступает в роли чувствительного инструмента для выявления и анализа отклонений в динамике охлаждения, предоставляя возможность более детального изучения факторов, влияющих на данный процесс.
Исследования показывают, что наблюдаемый квантовый эффект Мпембы может быть усилен и поддержан за счет определенных механизмов, таких как коллективное затухание и существование декогерентно-свободного подпространства. В частности, обнаружено, что время релаксации экспоненциально сокращается при наличии декогерентно-свободного подпространства, что свидетельствует о значительном улучшении по сравнению со стандартными релаксационными процессами. Это указывает на то, что в таких условиях система быстрее возвращается к равновесию, избегая типичной потери когерентности, которая замедляет охлаждение. $T_{relax} = e^{-k t}$ — примерное уравнение, описывающее данное ускорение, где $k$ — константа, зависящая от свойств декогерентно-свободного подпространства. Данные результаты подчеркивают важность сохранения квантовой когерентности для эффективного охлаждения и открывают новые возможности для разработки более быстрых и эффективных квантовых устройств.
Исследование, представленное в данной работе, демонстрирует, что ускоренная релаксация к равновесию в открытых квантовых системах возможна при грамотном использовании декогерентно-свободных подпространств и манипулировании начальными состояниями. Это напоминает о хрупкости любого научного построения. Как говорил Эрвин Шрёдингер: «Всё, что мы называем законом, может раствориться в горизонте событий». Подобно тому, как чёрная дыра поглощает свет, кажущиеся незыблемыми принципы могут оказаться преходящими, когда мы сталкиваемся с более глубоким пониманием квантовой реальности. Данная работа показывает, что даже в рамках марковской динамики и уравнения Линдблада, существует пространство для неожиданных эффектов, бросающих вызов интуитивным представлениям о тепловом равновесии.
Что дальше?
Представленная работа, исследуя квантический эффект Мпембы в открытых квантовых системах, лишь приоткрывает завесу над сложностью неравновесной термодинамики. Возможность ускорения релаксации через манипулирование начальными состояниями и использование декогерентно-свободных подпространств — это, несомненно, важный шаг. Однако, следует помнить: любое предсказание — лишь вероятность, и она может быть уничтожена силой гравитации, в данном случае, сложностью моделирования взаимодействий в реальных системах.
Очевидно, что необходимо расширить исследования за рамки марковских динамик. Немарковские эффекты, долговременные корреляции, и влияние окружения, которое не всегда можно считать «слабым», требуют глубокого анализа. Чёрные дыры не спорят; они поглощают, и аналогично, реальные квантовые системы могут скрывать механизмы, ускользающие от нашего упрощенного взгляда.
Поиск универсальных принципов, определяющих ускоренную релаксацию в различных системах, остаётся фундаментальной задачей. Возможно, ключ лежит не только в свойствах самой системы, но и в топологии её фазового пространства. Любая теория, которую мы строим, может исчезнуть в горизонте событий, но сам поиск истины — это уже победа.
Оригинал статьи: https://arxiv.org/pdf/2512.13509.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Все рецепты культистского круга в Escape from Tarkov
- Где находится точка эвакуации «Туннель контрабандистов» на локации «Интерчейндж» в Escape from Tarkov?
- Как завершить квест «Чистая мечта» в ARC Raiders?
- Как получить скины Alloyed Collective в Risk of Rain 2
- Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip
- Destiny 2 Equilibrium Dungeon Complete Guide
- Руководство по зимнему событию 2025 в The Division 2.
- Все облики в PEAK (и как их получить)
- Как посмотреть 4-ю серию острого соперничества онлайн и транслировать этот чувственный романтический сериал из любой точки мира.
- Решение головоломки с паролем Absolum в Yeldrim.
2025-12-17 01:41