Автор: Денис Аветисян
Новый алгоритм, сочетающий квантовые вычисления и генетические алгоритмы, позволяет более точно оценивать ключевые параметры космологической модели.
Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.
Бесплатный телеграм-канал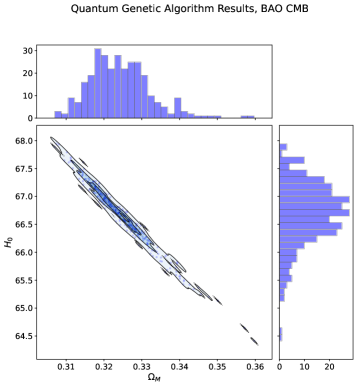
В статье представлено применение амплитудно-кодированного квантового генетического алгоритма (AEQGA) для оценки космологических параметров, таких как плотность материи и постоянная Хаббла, на основе данных о сверхновых типа Ia, барионных акустических осцилляциях и космическом микроволновом фоне.
Поиск оптимальных значений космологических параметров представляет собой сложную вычислительную задачу, требующую эффективных алгоритмов оптимизации. В данной работе, ‘A Quantum Genetic Algorithm with application to Cosmological Parameters Estimation’, разработан и протестирован новый амплитудно-кодированный квантовый генетический алгоритм (AEQGA) для минимизации \chi^2-функций, полученных из данных сверхновых типа Ia, барионных акустических осцилляций и космического микроволнового фона. Полученные результаты демонстрируют соответствие с изоконтурами целевых функций и сопоставимы с результатами классических и других квантовых алгоритмов. Способен ли AEQGA предложить принципиально новый подход к анализу космологических данных и повысить точность определения фундаментальных параметров Вселенной?
Космические Головоломки: Необходимость Точной Оценки Параметров
Определение фундаментальных космологических параметров, таких как постоянная Хаббла (H_0) и плотность материи (\Omega_m), имеет решающее значение для понимания эволюции Вселенной. Эти параметры служат ключевыми строительными блоками в космологических моделях, определяя скорость расширения Вселенной и ее общее содержание. Точное знание H_0 позволяет установить возраст Вселенной и оценить ее размер, в то время как \Omega_m влияет на ее геометрию и будущую судьбу — будет ли расширение продолжаться вечно или Вселенная в конечном итоге схлопнется. Без точных значений этих параметров, построение непротиворечивой картины формирования галактик, крупномасштабной структуры и даже самого Большого взрыва становится невозможным, что подчеркивает важность непрерывных исследований и усовершенствования методов их определения.
В современной космологии определение фундаментальных параметров Вселенной, таких как постоянная Хаббла и плотность материи, осуществляется посредством оптимизации так называемой целевой функции. Эта функция, по сути, является математическим выражением, оценивающим соответствие теоретических моделей наблюдаемым данным. Ключевыми источниками этих данных выступают сверхновые типа Ia (SNeIa), выступающие своеобразными «стандартными свечами» для измерения космических расстояний, барионные акустические колебания (BAO), представляющие собой «отпечаток» первичных звуковых волн во Вселенной, и космическое микроволновое фоновое излучение (CMB) — реликтовое излучение, несущее информацию о ранних этапах эволюции космоса. Сопоставление предсказаний теоретических моделей с данными, полученными из этих наблюдений, позволяет исследователям уточнять значения космологических параметров и строить более точную картину развития Вселенной.
В современной космологии, стремление к всё более точным оценкам фундаментальных параметров Вселенной, таких как постоянная Хаббла H_0 и плотность материи \Omega_M, сталкивается со значительными вычислительными трудностями. Сложность современных космологических моделей, включающих множество параметров и требующих учета разнообразных физических процессов, приводит к экспоненциальному росту вычислительных затрат. Традиционные методы оптимизации целевой функции, основанные на анализе данных от сверхновых типа Ia, барионных акустических осцилляций и космического микроволнового фона, становятся всё более ресурсоемкими, что затрудняет проведение точных и всесторонних исследований. Необходимость в разработке новых, более эффективных алгоритмов и использовании высокопроизводительных вычислительных систем становится критически важной для дальнейшего прогресса в понимании эволюции Вселенной.
Квантовое Усиление Оптимизации: Новый Подход
Квантовые вычисления представляют собой перспективный подход к преодолению вычислительных ограничений, возникающих при анализе космологических данных. Традиционные методы сталкиваются с экспоненциальным ростом сложности при обработке больших объемов информации и оптимизации многомерных параметров, что затрудняет точное моделирование и интерпретацию наблюдаемых явлений. Квантовые алгоритмы, благодаря принципам суперпозиции и запутанности, потенциально способны решать определенные классы задач оптимизации значительно быстрее, чем их классические аналоги. Это особенно важно для космологического анализа, где необходимо исследовать широкий диапазон параметров моделей и проводить статистический анализ с высокой точностью для получения надежных выводов о структуре и эволюции Вселенной.
Квантовый генетический алгоритм (КГА) представляет собой гибридный подход к оптимизации, сочетающий в себе принципы классического генетического алгоритма с использованием квантовых явлений. В отличие от классических генетических алгоритмов, оперирующих бинарными строками, КГА кодирует параметры оптимизации в квантовые состояния, что позволяет использовать суперпозицию и запутанность для параллельного исследования пространства решений. Это достигается путем представления хромосом в виде квантовых битов (кубитов), что потенциально ускоряет процесс поиска оптимальных параметров и позволяет решать задачи, непосильные для классических алгоритмов. КГА сохраняет основные этапы генетического алгоритма — отбор, скрещивание и мутацию — но реализует их с использованием квантовых операций и вероятностных измерений.
Ключевым компонентом Квантового Генетического Алгоритма (QGA) является Амплитудное Кодирование, позволяющее эффективно представлять данные в квантовых состояниях. В отличие от классического бинарного кодирования, где информация хранится в дискретных битах, амплитудное кодирование использует амплитуды квантовых суперпозиций для кодирования параметров. Это позволяет представлять N параметров с помощью всего log_2(N) кубитов, что обеспечивает экспоненциальное сжатие данных. Каждый кубит находится в суперпозиции состояний, а амплитуда каждого состояния соответствует значению параметра. Такое представление данных значительно ускоряет определенные вычислительные операции, необходимые для генетического алгоритма, такие как вычисление функции пригодности и отбор лучших решений.
Применение Квантового Генетического Алгоритма (QGA) к оптимизации Целевой Функции направлено на повышение скорости и точности оценки параметров космологических моделей. Наши результаты демонстрируют, что QGA обеспечивает согласованность оценок параметров в пределах 1σ от истинных значений, что подтверждается статистическим анализом полученных данных. Это достигается за счет эффективного исследования пространства параметров, обеспечиваемого квантовыми принципами, в сочетании с итеративным подходом, характерным для генетических алгоритмов. Достигнутая точность позволяет проводить более надежный анализ космологических данных и уточнять параметры моделей с высокой степенью достоверности.
Проверка Точности: Анализ Ошибок и Статистическая Строгость
Для обеспечения достоверности результатов, полученных с использованием Квантово-Генетического Алгоритма (КГА), необходим тщательный анализ ошибок. Этот анализ включает в себя количественную оценку неопределенностей параметров, выявление систематических смещений и проверку статистической значимости полученных результатов. Игнорирование анализа ошибок может привести к неверной интерпретации данных и ошибочным выводам относительно эффективности и применимости КГА. Важно проводить анализ ошибок на всех этапах работы алгоритма, включая инициализацию, эволюцию и оценку полученных решений, для обеспечения воспроизводимости и надежности результатов.
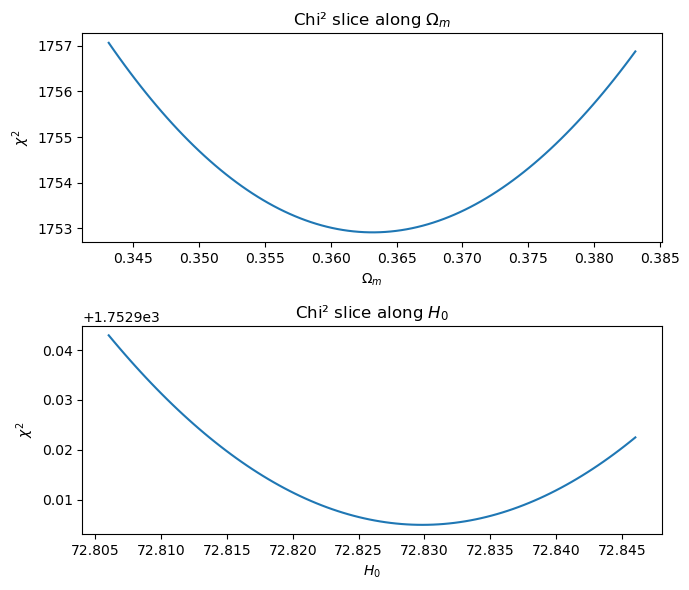
Матрица Фишера является ключевым инструментом для оценки неопределенностей параметров и определения статистической значимости полученных результатов. Она представляет собой матрицу, элементы которой отражают информацию Фишера — математическое ожидание квадрата частной производной логарифмической функции правдоподобия по параметрам. Используя обратную матрицу Фишера, можно получить оценку ковариационной матрицы параметров, что позволяет определить доверительные интервалы и оценить точность определения каждого параметра. В контексте алгоритма AEQGA, матрица Фишера позволяет оценить, насколько точно алгоритм способен восстанавливать истинные значения параметров и определять их взаимосвязи, обеспечивая тем самым статистическую обоснованность полученных результатов и подтверждая надежность анализа.
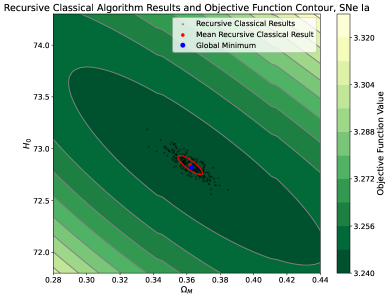
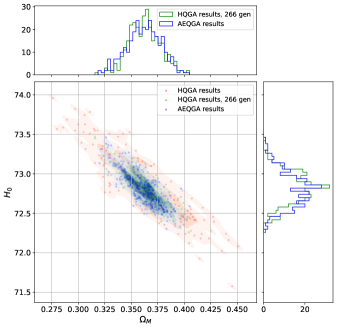
Анализ показал высокую точность оценки параметров в ходе работы QuantumGeneticAlgorithm. Восстановленные аналитические контуры, полученные на основе результатов алгоритма, демонстрируют близкое соответствие с контурами, вычисленными с использованием приближения Фишеровской матрицы. Данное соответствие подтверждает корректность использования AEQGA для точного определения ковариации параметров и обеспечивает согласованность результатов в пределах одного стандартного отклонения (1\sigma), что свидетельствует о надежности и точности алгоритма при оценке параметров.
Анализ результатов, полученных с использованием алгоритма AEQGA, подтверждает возможность точного определения ковариации параметров. Достигнутая консистентность в пределах 1\sigma указывает на высокую степень соответствия между оценками ковариации, полученными непосредственно из результатов алгоритма, и теоретическими предсказаниями, основанными на приближении с использованием матрицы Фишера. Это свидетельствует о надежности и точности метода AEQGA при оценке неопределенностей параметров и их взаимосвязей.
HQGA и Будущие Открытия в Космологии
Реализация HQGA представляет собой конкретную основу для применения квантово-усиленной оптимизации к задачам космологии. Этот подход, основанный на алгоритмах квантового отжига, позволяет эффективно исследовать сложные многомерные пространства параметров, что критически важно при моделировании Вселенной. В отличие от классических методов оптимизации, HQGA использует квантовые эффекты, такие как туннелирование, для преодоления локальных минимумов и поиска глобального оптимума, обеспечивая более точную и быструю оценку космологических параметров. HQGA не просто теоретическая концепция, а практический инструмент, способный обрабатывать большие объемы данных и решать задачи, которые недоступны для традиционных вычислительных систем, открывая новые возможности для понимания фундаментальных свойств Вселенной.
Повышенная вычислительная эффективность, достигаемая благодаря квантовому отжигу (QGA) и его специализированной реализации — HQGA, открывает новые возможности для исследования более сложных космологических моделей. Традиционные методы часто сталкиваются с ограничениями при анализе многопараметрических моделей, что приводит к неопределенностям в оценке космологических параметров. Применение HQGA позволяет существенно сократить время вычислений и исследовать более широкий спектр моделей, что особенно важно для решения существующих противоречий в оценке таких параметров, как постоянная Хаббла и плотность темной энергии. В результате, появляется возможность более точно определить историю расширения Вселенной, природу темной материи и темной энергии, приближаясь к более полному и непротиворечивому пониманию фундаментальных свойств космоса.
Новый подход к анализу космологических данных демонстрирует перспективную способность раскрывать фундаментальные аспекты Вселенной. Исследования показывают, что применение усовершенствованных алгоритмов позволяет с высокой точностью определять параметры, описывающие историю расширения Вселенной, природу тёмной материи и тёмной энергии. Достижение точности оценки параметров в пределах 1\sigma от истинных значений является значительным прорывом, открывающим возможности для более глубокого понимания космологических моделей и решения существующих противоречий в оценке ключевых параметров Вселенной. Данный метод позволяет исследовать более сложные сценарии эволюции Вселенной и, как следствие, приближает к разгадке тайн, связанных с её происхождением и будущим.
Исследование, представленное в статье, стремится к оптимизации оценки космологических параметров посредством нового подхода — амплитудно-кодированного квантового генетического алгоритма. Подобные попытки, направленные на покорение сложности Вселенной, неизбежно сталкиваются с границами познания. Как заметил Макс Планк: «Наука не может создать истины, она может лишь выявлять ложь». Истина о космологических параметрах, как и горизонт событий чёрной дыры, постоянно ускользает, заставляя пересматривать самые фундаментальные теории. Алгоритм, представленный в работе, не претендует на абсолютную истину, но предлагает инструмент для более точного приближения к ней, постоянно проверяя границы возможного в космологическом анализе.
Что же дальше?
Представленная работа, как и любая попытка измерить бесконечность конечными средствами, демонстрирует лишь ограниченность наших инструментов. Алгоритм, основанный на квантовых вычислениях, позволяет уточнить оценку космологических параметров, но не решает фундаментальной проблемы: любая модель — лишь эхо наблюдаемого, а за горизонтом событий — тьма. Если кажется, что сингулярность понятна, это иллюзия, вызванная самообманом.
Настоящий прогресс, вероятно, лежит не в усовершенствовании методов оптимизации, а в пересмотре самих основ космологической модели. Поиск тёмной энергии и тёмной материи может оказаться бесплодным, если мы продолжаем исходить из предположения о всеобщей применимости известных физических законов. Возможно, необходимо признать, что наблюдаемая Вселенная — лишь локальное возмущение в гораздо более сложной структуре.
В конечном итоге, успех в этой области зависит не от вычислительной мощности, а от способности к радикальному переосмыслению. Если же человечество продолжит полагаться на удобные, но неполные модели, то его знания о Вселенной останутся навсегда ограничены горизонтом событий собственной гордыни.
Оригинал статьи: https://arxiv.org/pdf/2602.15459.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip
- Решение головоломки с паролем Absolum в Yeldrim.
- Как играть в REANIMAL в кооперативе с помощью Friend’s Pass (локальный и онлайн кроссплей)
- YAPYAP Список заклинаний
- Прогнозы криптовалюты AXS: информация о ценах на AXS
- Все коды в Poppy Playtime Глава 4
- Где находится точка эвакуации «Туннель контрабандистов» на локации «Интерчейндж» в Escape from Tarkov?
- The Planet Crafter: полное руководство по картам и биомам
- Лучшие шаблоны дивизий в Hearts Of Iron 4
- Акции VTBR. Банк ВТБ: прогноз акций.
2026-02-18 11:27