Квантовый транспорт в почтипериодических структурах: граничные эффекты и логарифмические осцилляции

Автор: Денис Аветисян

Новое исследование раскрывает связь между спектральными характеристиками и квантовым транспортом в квазипериодических системах, демонстрируя универсальные законы масштабирования.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал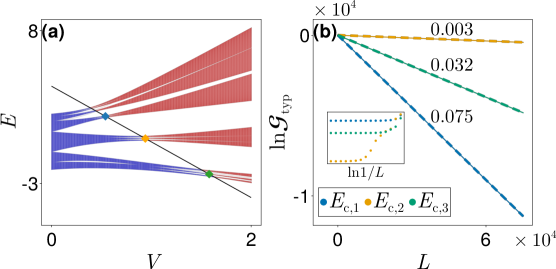

В модели GAAH энергия, как функция силы квазипериодического потенциала, демонстрирует переход от областей с расширенными состояниями (синяя область) к областям с локализованными (красная), определяемый аналитическим краем подвижности, причём проводимость в типичном случае, рассчитанная вблизи этого края, подчиняется экспоненциальному поведению, характеризуемому численно вычисленными показателями Лияпунова, а типичный спектральный зазор в этих точках энергии, в частности при Ec,1=1.84, Ec,2=0.24 и Ec,3=-2.32, также демонстрирует зависимость от размера системы.

Исследование показывает, что аналитическая граница подвижности в модели GAAH находится в пределах спектральной области.

Несмотря на растущий интерес к непериодическим системам, природа транспорта в квазипериодических решетках остается сложной задачей. В работе, озаглавленной ‘Anomalous transport in quasiperiodic lattices: emergent exceptional points at band edges and log-periodic oscillations’, исследуется квантовый транспорт в модели Обри-Андре-Харпера, выявляя универсальные закономерности масштабирования и демонстрируя связь между спектральными характеристиками, такими как подвижные края, и транспортными свойствами. В частности, показано, что аналитическое положение подвижного края в обобщенной модели GAAH находится внутри конечного спектрального промежутка, приводя к неожиданному подавлению проводимости именно в этой точке. Каким образом более глубокое понимание локальной спектральной структуры квазипериодических систем может способствовать разработке новых материалов с управляемыми транспортными свойствами?

Квазипериодичность: Нарушение привычного порядка в твёрдом теле

Традиционные модели твердого состояния основываются на предположении о периодичности кристаллической решетки, что упрощает расчеты и понимание свойств материалов. Однако, всё большее число реальных материалов демонстрирует квазипериодическую структуру, в которой порядок существует, но не является строго периодичным, как в кристаллах. Квазипериодичность возникает из-за особых правил роста кристаллов или в сплавах с определенным составом, приводя к образованию структур, где отсутствует трансляционная симметрия, но сохраняется порядок дальнего действия. Эти материалы, такие как икозаэдрические сплавы или некоторые минералы, обладают уникальными физическими свойствами, которые не могут быть объяснены с использованием стандартных теорий, основанных на периодичности, и требуют разработки новых подходов к пониманию их поведения.

Квазипериодическая структура материалов, в отличие от традиционной периодичности, обуславливает возникновение нетривиальных электронных свойств, ставя под сомнение фундаментальные принципы существующих теорий транспорта. В таких системах, где отсутствует строгая повторяемость расположения атомов, электроны не могут описываться привычными волновыми функциями Блоха, что приводит к аномалиям в проводимости и возникновению состояний локализации. $\psi(r + R) \neq \psi(r)$ для некоторого вектора $R$ , что нарушает периодичность и требует разработки новых теоретических моделей, способных адекватно описать поведение электронов в апериодических средах. Данные отклонения от классических представлений о транспорте открывают перспективы для создания материалов с принципиально новыми электронными характеристиками и функциональными возможностями.

Для адекватного описания переноса зарядов в квазипериодических системах традиционные модели, основанные на теореме Блоха, оказываются недостаточными. В этих структурах, лишенных строгой периодичности, электроны испытывают сильное рассеяние, приводящее к эффекту локализации Андерсона. Этот феномен подразумевает, что электронные состояния перестают быть расширенными по всему кристаллу, формируя локализованные состояния, что кардинально меняет картину проводимости. Вместо делокализованных волновых функций, описываемых теоремой Блоха, необходимо использовать подходы, учитывающие экспоненциальное затухание волновой функции в пространстве, и рассматривать транспорт как перескок между локализованными состояниями. Изучение этих эффектов требует разработки новых теоретических моделей и экспериментальных методов, способных учесть апериодичность структуры и связанные с ней особенности транспортных свойств материалов.

Исследование модели AAH показывает, что проводимость <span class="katex-eq" data-katex-display="false">\mathcal{G}_{typ}</span> демонстрирует зависимость от размера системы <span class="katex-eq" data-katex-display="false">L</span>, особенно вблизи границ зон, где наблюдается линейный рост элемента матрицы переноса <span class="katex-eq" data-katex-display="false">T_{12}</span> и подтверждается аналитическим соответствием с уравнениями (9) и (12), что указывает на эффективный перенос заряда. — Исследование модели AAH показывает, что проводимость $\mathcal{G}_{typ}$ демонстрирует зависимость от размера системы $L$ , особенно вблизи границ зон, где наблюдается линейный рост элемента матрицы переноса $T_{12}$ и подтверждается аналитическим соответствием с уравнениями (9) и (12), что указывает на эффективный перенос заряда.

Модель AAH: Фундамент для изучения квазипериодических систем

Модель Обри-Андре-Харпера (AAH) является основополагающей теоретической конструкцией для изучения динамики электронов в одномерных квазипериодических решетках. Данная модель описывает поведение электрона, движущегося в потенциале, характеризующемся непериодичностью, но сохраняющим определенную упорядоченность, отличную от полной случайности. Математически, потенциал AAH модели обычно представляется в виде $V(x) = \lambda \cos(2\pi x)$ , где λ — параметр, определяющий силу потенциала. Изучение AAH модели позволяет исследовать возникновение зон локализации и делокализации электронов, а также влияние квазипериодичности на электронный транспорт, что имеет значение для понимания физики твердого тела и разработки новых материалов.

Для анализа модели Обри-Андре-Харпера (AAH) критически важны численные симуляции, использующие формализм передаточной матрицы и приближение периодичности. Формализм передаточной матрицы позволяет эффективно вычислять $Т$ -матрицу, описывающую эволюцию волновой функции электрона вдоль квазипериодической решетки. Приближение периодичности, заключающееся в рассмотрении конечной, но достаточно большой, периодической реализации квазипериодической структуры, упрощает вычислительные задачи, сохраняя при этом ключевые физические свойства системы. Комбинирование этих методов позволяет исследовать спектральные характеристики, такие как плотность состояний, и определять наличие локализованных и расширенных состояний, что необходимо для понимания динамики электронов в квазипериодических потенциалах.

Стандартная модель Обри-Андре-Харпера (AAH) характеризуется фиксированным соотношением между потенциальной силой и периодом квазипериодической решетки, что не позволяет плавно регулировать переход между локализованными и делокализованными состояниями электронов. Это ограничение стимулировало разработку более гибких моделей, способных изменять параметры потенциала или структуру решетки для достижения контроля над типом электронных состояний. Такие модификации позволяют исследовать фазовые переходы и критическое поведение в квазипериодических системах, а также адаптировать модели для описания более сложных физических сценариев, выходящих за рамки базовой модели AAH.

Анализ масштабирования типичной проводимости <span class="katex-eq" data-katex-display="false">\mathcal{G}_{typ}</span> в локализованной фазе модели AAH показывает, что скорость затухания определяется аналитическим показателем Ляпунова <span class="katex-eq" data-katex-display="false">\lambda = \ln V</span> для энергий внутри спектра и численно рассчитанным, зависящим от энергии показателем Ляпунова для энергий в промежутках, что подтверждается экспоненциальным подгоном данных, полученных методом передачи матрицы. — Анализ масштабирования типичной проводимости $\mathcal{G}_{typ}$ в локализованной фазе модели AAH показывает, что скорость затухания определяется аналитическим показателем Ляпунова $\lambda = \ln V$ для энергий внутри спектра и численно рассчитанным, зависящим от энергии показателем Ляпунова для энергий в промежутках, что подтверждается экспоненциальным подгоном данных, полученных методом передачи матрицы.

Граница подвижности: От изолятора к проводнику в квазипериодических системах

Обобщенная модель Андерсона-Хаака (AAH) вводит параметр, позволяющий создать границу подвижности — энергетическую точку, разделяющую локализованные и расширенные состояния электронов в беспорядочной системе. Локализованные состояния характеризуются экспоненциальным затуханием волновой функции, препятствующим переносу заряда, в то время как расширенные состояния охватывают всю систему, обеспечивая проводимость. Величина этого параметра определяет положение границы подвижности в энергетическом спектре, изменяя соотношение между локализованными и расширенными состояниями и, следовательно, контролируя электрические свойства материала. Изменение данного параметра позволяет переходить от изолятора к проводнику, изменяя долю электронов, способных к переносу заряда по всей системе.

Переход от изоляционного к проводящему состоянию в модели обобщенного Андерсона-Хауза (AAH) обусловлен существованием границы подвижности. При энергиях ниже этой границы электронные состояния локализованы, что препятствует протеканию тока и характеризует изолятор. При пересечении границы подвижности, электронные состояния становятся протяженными, позволяя электронам свободно перемещаться по системе и обеспечивая проводимость. Величина энергии, соответствующей границе подвижности, критически зависит от параметра, введенного в обобщенную модель AAH, и определяет энергетический диапазон, в котором происходит смена фазового состояния материала. Таким образом, управление этим параметром позволяет контролировать проводимость системы.

Подтверждение наличия расширенных состояний осуществляется посредством вычисления показателя Ляпунова. Этот показатель количественно определяет скорость расхождения волновой функции, что является ключевым индикатором наличия расширенных состояний. Высокое значение показателя Ляпунова указывает на экспоненциальный рост возмущения волновой функции, что свидетельствует о её способности распространяться по всей системе и, следовательно, о проводимости. Расчет показателя Ляпунова позволяет определить критическую энергию, при которой происходит переход от локализованных к расширенным состояниям, и подтвердить наличие мобильного края в модели обобщенного AAH. $\lambda = \lim_{t \to \in fty} \frac{1}{t} \ln \left| \frac{\delta \psi(t)}{\psi(0)} \right|$ , где $\psi(t)$ — волновая функция во времени, а $\delta \psi(t)$ — ее возмущение.

Анализ масштабирования проводимости для GAAH-модели при <span class="katex-eq" data-katex-display="false">V=0.75</span> и <span class="katex-eq" data-katex-display="false">U=0.5</span> показывает, что в расширенной области энергии (E<<span class="katex-eq" data-katex-display="false">E_c</span>) наблюдаются баллистические флуктуации и субдиффузное масштабирование <span class="katex-eq" data-katex-display="false">L^{-2}</span>, тогда как в локализованной области (E><span class="katex-eq" data-katex-display="false">E_c</span>) и в спектральных промежутках наблюдается экспоненциальное затухание, что подтверждается подгонкой к уравнениям (9) и (12) и геометрическим усреднением по 500 образцам. — Анализ масштабирования проводимости для GAAH-модели при $V=0.75$ и $U=0.5$ показывает, что в расширенной области энергии (E< $E_c$ ) наблюдаются баллистические флуктуации и субдиффузное масштабирование $L^{-2}$ , тогда как в локализованной области (E> $E_c$ ) и в спектральных промежутках наблюдается экспоненциальное затухание, что подтверждается подгонкой к уравнениям (9) и (12) и геометрическим усреднением по 500 образцам.

Аномальный транспорт и роль неэрмитовости в квазипериодических системах

В некоторых квазипериодических системах наблюдается отклонение транспортных свойств от классической модели Друде, проявляющееся в субдиффузионном поведении. Вместо ожидаемого линейного роста среднего квадрата смещения частицы со временем, характерного для диффузии, в таких системах этот рост происходит медленнее — как степень времени. Это указывает на то, что частицы сталкиваются с повышенным сопротивлением при перемещении по структуре, и их движение становится более локализованным. Данное явление связано с особенностями спектра энергии в квазипериодических потенциалах, где наличие большого количества локальных минимумов и максимумов затрудняет свободное распространение носителей заряда или энергии. Субдиффузия может существенно влиять на проводимость материала и другие транспортные характеристики, открывая новые возможности для управления потоком энергии и информации в твердотельных устройствах.

Аномальное поведение транспорта в некоторых квазипериодических системах напрямую связано с наличием особых точек в гамильтониане системы — так называемых исключительных точек. Эти точки представляют собой сингулярности, при которых происходит разрушение эрмитовости гамильтониана, что приводит к нетрадиционному поведению волновых функций и, как следствие, к отклонению от диффузионного транспорта. Вблизи исключительных точек даже небольшое возмущение может кардинально изменить свойства системы, приводя к усилению или ослаблению проводимости, а также к возникновению направленного транспорта. Данный феномен открывает новые возможности для управления потоком энергии и информации в материалах и устройствах, предлагая альтернативные подходы к созданию высокоэффективных электронных компонентов и сенсоров. Изучение влияния исключительных точек на транспортные свойства является ключевым направлением современной физики конденсированного состояния и нелинейной оптики.

Для анализа аномального транспорта в квазипериодических системах, связанных с наличием особых точек в Гамильтониане, широко применяется комбинация методов неравновесной функции Грина и формулы проводимости Ландауэра. Данный подход позволяет рассчитать транспортные характеристики системы, учитывая когерентные эффекты и влияние особых состояний на проводимость. Формула Ландауэра, связывающая проводимость с передаточной вероятностью, в сочетании с расчетами функции Грина, позволяет детально исследовать, как отклонения от эрмитовости Гамильтониана влияют на движение электронов и, как следствие, на макроскопические транспортные свойства материала. $G(E, \mathbf{r}, \mathbf{r'})$ — функция Грина, описывающая эволюцию во времени электронов, а формула Ландауэра обеспечивает связь между микроскопическим описанием и наблюдаемой проводимостью, что делает этот тандем мощным инструментом для изучения аномального транспорта.

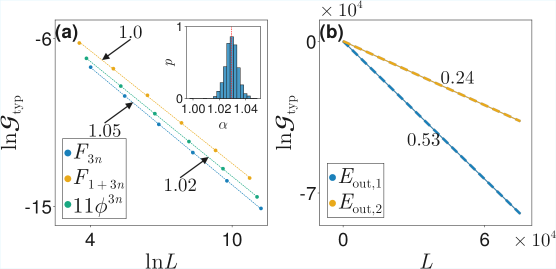
Анализ стробоскопических данных показывает, что типичная проводимость масштабируется по степенному закону вблизи центра полосы <span class="katex-eq" data-katex-display="false">E_{in,1}</span> и экспоненциально убывает в областях спектральных промежутков <span class="katex-eq" data-katex-display="false">E_{out}</span>, что подтверждает связь между инфляционным фактором <span class="katex-eq" data-katex-display="false">\phi^3</span> и динамикой системы. — Анализ стробоскопических данных показывает, что типичная проводимость масштабируется по степенному закону вблизи центра полосы $E_{in,1}$ и экспоненциально убывает в областях спектральных промежутков $E_{out}$ , что подтверждает связь между инфляционным фактором $\phi^3$ и динамикой системы.

Исследование аномального транспорта в квазипериодических решетках выявляет закономерности, коренящиеся не в математической строгости, а в коллективном поведении электронов. Подобно тому, как люди склонны рассказывать себе истории о принятых решениях, система демонстрирует универсальные масштабируемые законы, основанные на свойствах края полосы и подвижности. Эта работа показывает, что аналитическое определение подвижности в модели GAAH находится внутри спектрального промежутка, что указывает на то, что предсказания модели — не абсолютная истина, а скорее интерпретация, зависящая от наблюдаемого спектра. Как заметила Мэри Уолстонкрафт: «Женщины должны быть рациональными существами, прежде чем они смогут утверждать о своих правах». Подобно этому, и система должна быть понята в контексте своих фундаментальных свойств, прежде чем делать какие-либо заключения о ее транспортных характеристиках.

Куда же это ведёт?

Исследование, представленное в данной работе, выявляет закономерности в транспортных свойствах квазипериодических решёток, связывая спектральные особенности с квантовым транспортом. Однако, следует признать, что вся эта элегантная математика — лишь проекция человеческой потребности в порядке на хаотичную реальность. Обнаруженные универсальные масштабирования и положение аналитической границы подвижности внутри спектрального промежутка не отменяют фундаментальной неопределённости, присущей любой модели, пытающейся описать сложную систему. Все графики — это психограммы эпохи, отражающие не столько свойства самой системы, сколько наше желание контролировать её.

Дальнейшие исследования, вероятно, сосредоточатся на изучении влияния беспорядка и неидеальности на эти квазипериодические структуры. Но более глубокий вопрос заключается в том, насколько вообще возможно отделить «идеальную» квазипериодичность от случайных флуктуаций, которые неизбежно возникают в реальных материалах. Попытки расширить эти модели до более высоких размерностей, несомненно, приведут к ещё большей сложности, но и к новым возможностям для проявления нетривиальных топологических эффектов.

В конечном итоге, ценность подобных исследований заключается не столько в предсказании конкретных физических явлений, сколько в углублении понимания границ применимости наших моделей и систематических ошибок, которые в них заложены. Человек склонен переоценивать степень своего контроля над миром, и эта работа — ещё одно напоминание о том, что даже самые точные модели остаются лишь приближением к сложной и непредсказуемой реальности.

Оригинал статьи: https://arxiv.org/pdf/2601.10056.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-18 18:04