Магнетизм и загадки спиновой жидкости Kitaev

Автор: Денис Аветисян

В статье представлен обзор последних теоретических и численных исследований фазовых переходов, индуцированных магнитным полем, в модели Kitaev, описывающей экзотическое состояние квантовой спиновой жидкости.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал

Расширенная модель Китаяева демонстрирует зависимость удельной теплоемкости от магнитного поля, приложенного в направлении [111], и температуры, выявляя границы фаз и характерные температурные масштабы, в то время как пространственные колебания локальной плотности состояний в монослое α-RuCl3 указывают на существование безмассовых майорановских фермионов, аналогичных осцилляциям Фриделя спинонов.

Исследование фазовых переходов и нетрадиционной динамики в модели Kitaev под воздействием магнитного поля, включая появление металлического состояния Майораны.

Несмотря на теоретическую предсказуемость, экспериментальное подтверждение существования квантовых спиновых жидкостей остается сложной задачей. Настоящий обзор посвящен исследованию магнитных явлений, возникающих в спиновых жидкостях типа Китая, в частности, в работе ‘Magnetic field induced phenomena in Kitaev spin liquids’. В ней показано, что при приложении магнитного поля в таких системах возникают новые фазы, включая квантовый металл Майораны, характеризующиеся специфическими динамическими свойствами дробных квазичастиц. Какие экспериментальные методы, такие как нейтронная рассеяние или спектроскопия, позволят однозначно идентифицировать эти фазы и подтвердить существование спиновых жидкостей в реальных материалах?

За гранью магнетизма: Знакомство с моделью Китаева

Традиционные модели квантового магнетизма, стремясь к упрощению расчетов, часто опускают ключевые взаимодействия и детали, присущие реальным материалам. Это приводит к тому, что предсказанные ими магнитные фазы не соответствуют наблюдаемым в природе, особенно когда речь идет об экзотических состояниях вещества, таких как спиновые жидкости. Упрощения, необходимые для аналитического решения, искажают сложность квантовых систем, не позволяя выявить новые и неожиданные магнитные явления. В результате, понимание и предсказание поведения магнитных материалов на микроскопическом уровне сталкивается с серьезными ограничениями, что требует разработки более адекватных и точных теоретических подходов.

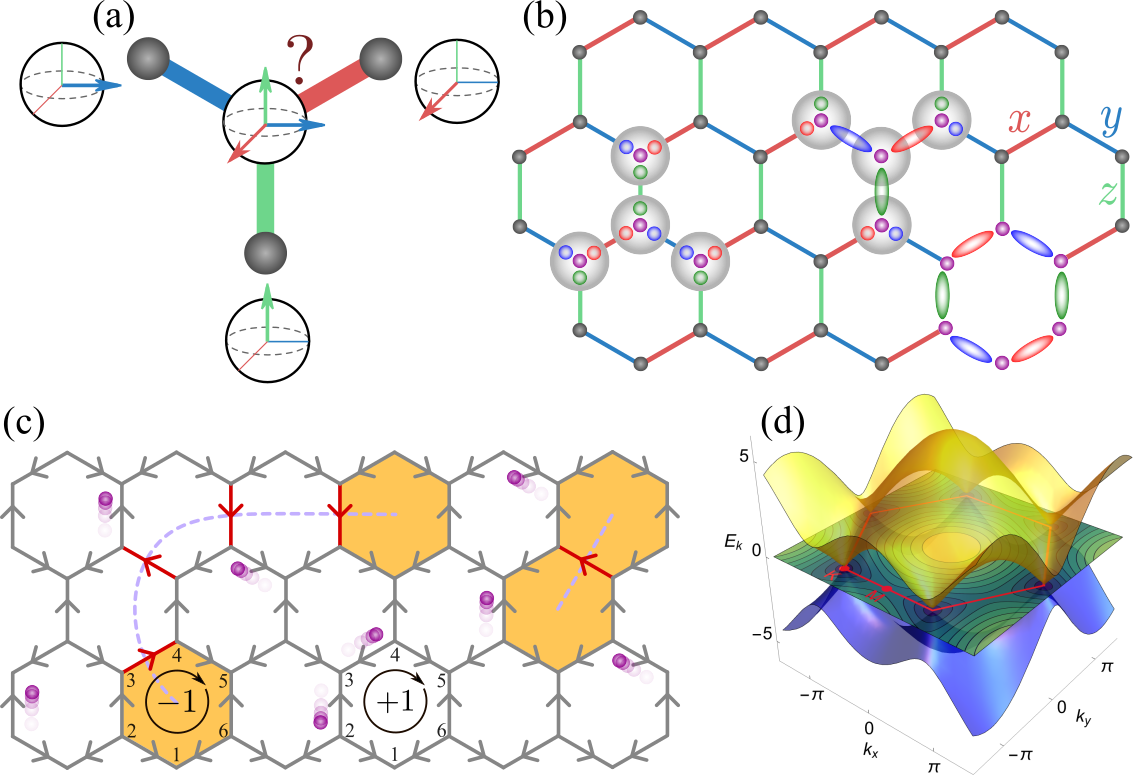
Модель Китаева на сотовой решетке представляет собой принципиально новый подход к изучению квантовых спиновых жидкостей, отличающийся от традиционных методов. В отличие от большинства моделей, не имеющих аналитических решений, модель Китаева допускает точное решение, что позволяет исследователям детально изучить её свойства и предсказать поведение. Это достигается за счет уникальной структуры взаимодействия между спинами, где взаимодействие зависит от конкретной связи между соседними спинами на сотовой решетке. Такое решение открывает возможность понять, как возникают экзотические фазы материи, характеризующиеся отсутствием магнитного порядка даже при абсолютном нуле температуры, и служит основой для разработки новых материалов с необычными квантовыми свойствами. $S_i \cdot S_j$ — это взаимодействие, которое в модели Китаева не является изотропным и зависит от направления связи.

Модель Китаева, в отличие от традиционных магнитных систем, характеризуется уникальным взаимодействием между спинами, зависящим от конкретной связи между ними. Вместо однородных взаимодействий, как в классических моделях, в модели Китаи спины на соседних звеньях сотовой структуры взаимодействуют по-разному, что приводит к появлению экзотических состояний материи. Такой подход позволяет реализовать фракционирование спинов на майорановские фермионы — квазичастицы, являющиеся собственными античастицами, и, как следствие, к возникновению квантовых спиновых жидкостей, где спины не упорядочиваются даже при абсолютном нуле температуры. Это открытие имеет потенциальное значение для создания топологических кубитов — основы для устойчивых квантовых вычислений, поскольку майорановские фермионы обладают высокой устойчивостью к декогеренции. Изучение этих взаимодействий открывает новые горизонты в понимании фундаментальных свойств материи и разработке инновационных квантовых технологий.

В модели Китая с анизотропными взаимодействиями и слабым магнитным полем, квазичастицы демонстрируют ограниченную динамику - одиночные частицы остаются неподвижными, а двухчастичные композиты приобретают частичную подвижность вдоль одномерного направления, что эквивалентно различным моделям, связанным между собой преобразованиями дуальности и вращениями. — В модели Китая с анизотропными взаимодействиями и слабым магнитным полем, квазичастицы демонстрируют ограниченную динамику — одиночные частицы остаются неподвижными, а двухчастичные композиты приобретают частичную подвижность вдоль одномерного направления, что эквивалентно различным моделям, связанным между собой преобразованиями дуальности и вращениями.

Возникающие возбуждения: Z2-поток и майорановские фермионы

В отличие от традиционного магнетизма, где элементарными возбуждениями являются спиновые волны или магнеоны, модель Китаева предсказывает возникновение дробных квазичастиц — Z2-флюкса и майорановских фермионов. Это означает, что магнитные моменты в модели не просто претерпевают небольшие отклонения, а распадаются на новые, независимые объекты. Z2-флюкс представляет собой топологический дефект, характеризующийся нетривиальной топологией, а майорановские фермионы — это частицы, являющиеся своими собственными античастицами. Появление таких дробных возбуждений является прямым следствием особого характера взаимодействия спинов в модели Китаева и отличает ее от классических магнитных систем.

В отличие от традиционных возбуждений в магнитных системах, квазичастицы, возникающие в модели Китаева, не являются просто возмущениями спинов электронов. Они представляют собой коллективные состояния, возникающие как результат сильных корреляций между спинами, и обладают уникальной статистикой обмена. Это означает, что при перестановке двух таких частиц волновая функция системы может измениться не на фактор +1 (как для бозонов или фермионов), а на -1 или вообще остаться неизменной, что ведет к нетривиальной топологической структуре системы и появлению новых физических явлений. Данная особенность является следствием фракционализации степеней свободы электронов и возникновения квазичастиц с дробным зарядом и спином.

Майорановские фермионы, частицы, являющиеся собственными античастицами, представляют собой ключевой признак топологического порядка. В отличие от обычных фермионов, для которых требуется отдельная античастица, майорановские фермионы характеризуются нулевой энергией и локализованы в дефектах материала. Их существование обусловлено не локальными свойствами частиц, а глобальной топологией волновой функции системы. Обнаружение майорановских фермионов является сложной задачей, требующей специализированных методов, но их подтверждение служит убедительным доказательством возникновения нетривиальной топологической фазы материи и открывает возможности для создания устойчивых кубитов в квантовых вычислениях.

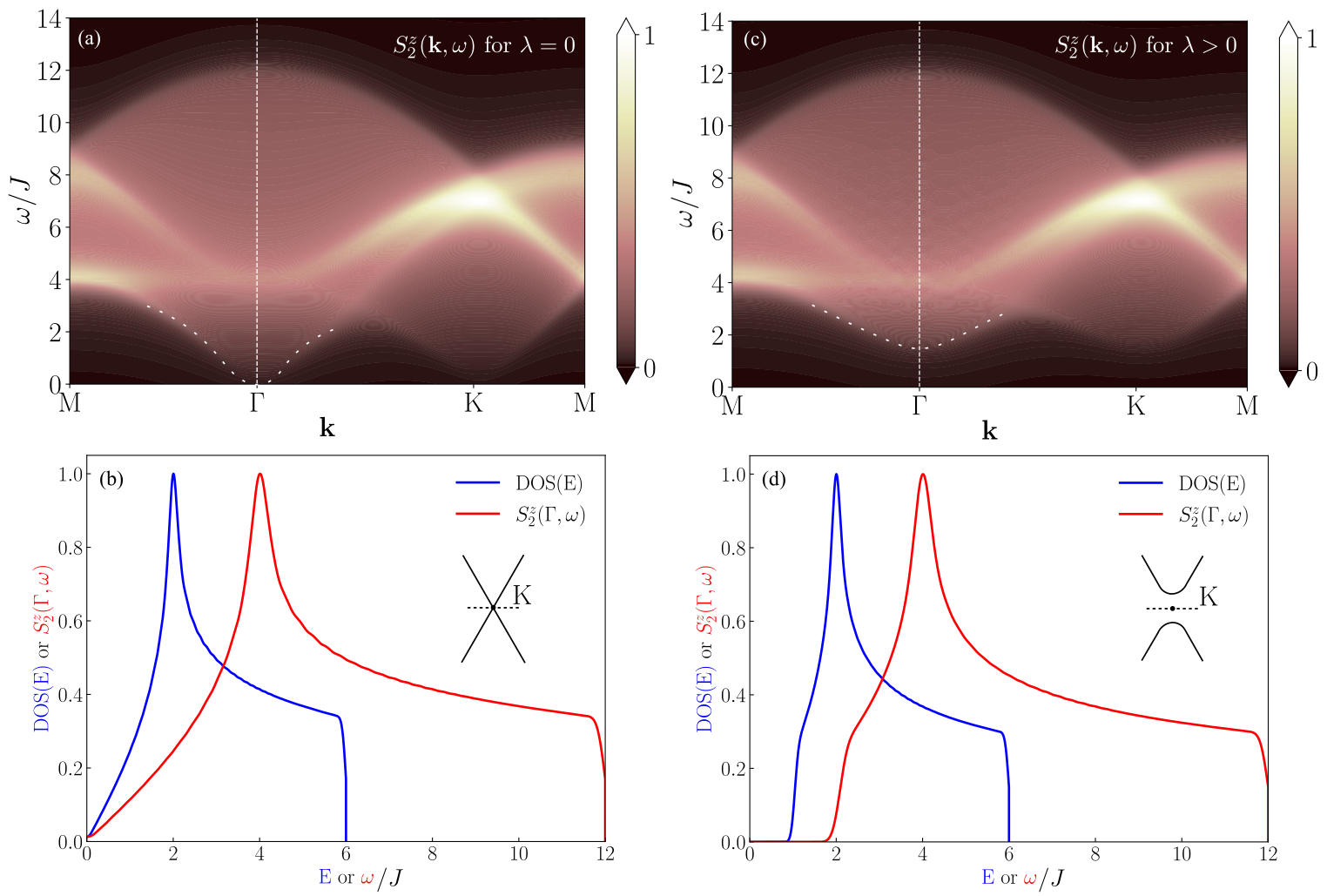
Динамическая спиновая структура <span class="katex-eq" data-katex-display="false">S_{2}(\mathbf{k},\omega)</span> для изотропной антиферромагнитной модели Китаева демонстрирует соответствие между спиновым спектром и плотностью состояний дираковских майорановских фермионов, особенно выраженное при нулевой температуре и нарушении симметрии относительно обращения времени, что позволяет напрямую наблюдать майорановские состояния в спектре димеров. — Динамическая спиновая структура $S_{2}(\mathbf{k},\omega)$ для изотропной антиферромагнитной модели Китаева демонстрирует соответствие между спиновым спектром и плотностью состояний дираковских майорановских фермионов, особенно выраженное при нулевой температуре и нарушении симметрии относительно обращения времени, что позволяет напрямую наблюдать майорановские состояния в спектре димеров.

Прощупывание квантовой спиновой жидкости

Характеризация квантовой спиновой жидкости представляет значительные вычислительные трудности из-за сильной корреляции между спиновыми степенями свободы. Традиционные методы, применяемые к системам с независимыми или слабо взаимодействующими частицами, оказываются неэффективными. Для преодоления этих сложностей требуется использование продвинутых численных подходов, таких как метод ренормгруппы плотности матрицы (DMRG) для одномерных систем и бесконечные проективные запутанные парные состояния (iPEPS) для двумерных систем. Эти методы позволяют исследовать основные свойства основного состояния и обнаруживать экзотические фазы материи, характерные для квантовых спиновых жидкостей, включая отсутствие магнитного порядка и наличие фракционированных возбуждений.

Метод численного моделирования — метод перенормированной матрицы плотности (DMRG) — демонстрирует высокую эффективность при исследовании одномерных систем. Он основан на последовательном приближении к основному состоянию системы путем удержания лишь наиболее значимых состояний в гильбертовом пространстве. Этот подход позволяет с высокой точностью рассчитывать энергию основного состояния, корреляционные функции и другие свойства системы, даже для моделей с сильным взаимодействием. DMRG особенно полезен для изучения спиновых цепей и других одномерных квантовых систем, предоставляя важные данные для понимания их фундаментальных свойств и фазовых переходов. Точность метода снижается при увеличении размерности системы, однако он остается ключевым инструментом для изучения одномерных моделей.

Бесконечные проецируемые запутанные парные состояния (iPEPS) представляют собой расширение методов, используемых для изучения одномерных систем, на двумерные модели. Данный подход критически важен для исследования модели Китаева, являющейся ключевой в контексте квантовых спиновых жидкостей. Недавние численные расчеты с использованием iPEPS подтвердили наличие конечной плотности состояний при нулевой энергии, что является одним из признаков отсутствия магнитного порядка и подтверждает гипотезу о квантово-спиновой жидкости в данной модели. Это позволяет детально исследовать свойства возбуждений и корреляции в системе, недоступные для классических методов.

Двумерные квантовые спиновые жидкости могут переходить в различные фазы, включая гapped (с разрывом в энергии, обладающие топологическим порядком и, возможно, хиральными краевыми модами) и gapless (без разрыва, такие как спиновый ферми-жидкий металл или тепловой металл), в зависимости от их свойств и порядка.

За пределами идеала: Переход размерности и реальные материалы

В реальности, воплощение теоретических моделей, таких как идеальная китаевская сотовая решетка, сталкивается с неизбежными отклонениями в материалах. Кристаллическая структура, наличие дефектов и взаимодействие между различными компонентами приводят к искажениям, которые влияют на наблюдаемые физические свойства. Эти несовершенства не просто вносят поправки к теории, но и могут приводить к появлению новых, неожиданных явлений. Изучение этих отклонений крайне важно для понимания поведения реальных материалов и разработки новых квантовых технологий, поскольку даже небольшие изменения в структуре могут существенно повлиять на стабильность и свойства экзотических фаз материи, таких как квантовая спиновая жидкость.

Переход между размерностями, или изменение эффективной размерности системы, играет ключевую роль в понимании поведения квази-одномерных материалов. В таких системах, где один из параметров пространства значительно превосходит остальные, взаимодействие между элементами может приводить к неожиданным эффектам. Например, в материалах, близких к одномерным цепочкам, увеличение давления или магнитного поля может привести к усилению межцепочечного взаимодействия, эффективно повышая размерность системы и изменяя её физические свойства. Этот переход не всегда является резким; зачастую наблюдается постепенное изменение характеристик, что требует детального анализа для определения преобладающего режима поведения. Понимание механизмов, лежащих в основе этого перехода, необходимо для разработки новых материалов с заданными свойствами и управления их поведением в различных условиях.

Стабильность квантовой спиновой жидкости, экзотического состояния материи, напрямую зависит от баланса между размерностью системы и характером взаимодействий между спинами. Исследования показывают, что при сильных магнитных полях в квази-одномерных материалах наблюдается переход к доминирующему одномерному поведению. Это явление предполагает, что спиновые цепочки, ранее связанные в более сложную структуру, эффективно разъединяются, теряя свои межцепочечные взаимодействия. По сути, система перестраивается таким образом, что спины преимущественно выстраиваются вдоль одной размерности, что приводит к упрощению ее магнитных свойств и, возможно, к подавлению экзотических явлений, характерных для квантовой спиновой жидкости. Такое поведение подчеркивает важность контроля размерности и взаимодействия для создания и поддержания этого необычного состояния материи.

Анизотропная модель Китаева на сотовой решетке отображается на эффективную квадратную решетку димеров спинов, где двухкомпонентные степени свободы τ на связях представлены парами спинов <span class="katex-eq" data-katex-display="false"> \sigma^{\alpha} </span> на z-связях, а эффективные стабилизаторы обозначены разными цветами. — Анизотропная модель Китаева на сотовой решетке отображается на эффективную квадратную решетку димеров спинов, где двухкомпонентные степени свободы τ на связях представлены парами спинов $\sigma^{\alpha}$ на z-связях, а эффективные стабилизаторы обозначены разными цветами.

Топологические сигнатуры и будущие направления

Наличие неабелевых любыхонов, в частности, майорановских фермионов, открывает принципиально новый подход к созданию отказоустойчивых квантовых компьютеров. В отличие от традиционных кубитов, подверженных декогеренции из-за взаимодействия с окружающей средой, информация, закодированная в неабелевых любыхонах, защищена топологическим образом. Это означает, что небольшие локальные возмущения не могут изменить квантовое состояние, поскольку для этого потребовалось бы изменить топологию системы — процесс, требующий значительной энергии. Таким образом, майорановские фермионы представляют собой перспективные кандидаты для реализации кубитов, способных сохранять квантовую когерентность на достаточно длительное время, необходимое для проведения сложных квантовых вычислений. Исследования в этой области направлены на создание и контроль систем, в которых можно реализовать и манипулировать этими экзотическими квазичастицами, что позволит в будущем создать принципиально новые типы квантовых устройств.

Для подтверждения топологического порядка и выявления экзотических квазичастиц, таких как майорановские фермионы, ключевыми задачами экспериментальных исследований являются измерения спиновой структуры рассеяния и изучение хиральных краевых состояний. Спиновая структура рассеяния позволяет определить характер спиновых корреляций в материале, указывая на наличие нетривиальной топологической фазы. В свою очередь, исследование хиральных краевых состояний — проводящих каналов на границе материала, обладающих уникальными свойствами, обусловленными топологической защитой — дает прямые доказательства существования топологического порядка и позволяет изучать поведение квазичастиц на этих состояниях. Успешное обнаружение и характеристика этих признаков откроет путь к созданию надежных квантовых устройств, устойчивых к декогеренции и ошибкам.

Активный поиск и разработка новых квантовых материалов с топологическими свойствами открывает перспективные пути к созданию устойчивых квантовых устройств. Недавние исследования продемонстрировали существование материалов, демонстрирующих нулевой флюксус-разрыв — характеристику, согласующуюся с концепцией «Майорановского металла». Это открытие указывает на возможность реализации неабелевых экситонов, таких как майорановские фермионы, которые обладают потенциалом для создания квантовых битов, устойчивых к декогеренции и, следовательно, подходящих для надежных квантовых вычислений. Подобные материалы, обладающие уникальными электронными свойствами и защищенными состояниями на краях, могут стать основой для принципиально новых технологий в области квантовой информации и вычислений.

В модели сотовой структуры с спин-орбитальной фрустрацией, локальные спиновые степени свободы расщепляются на четыре майорановских фермиона, образующих связанные пары и определяющие локальное <span class="katex-eq" data-katex-display="false">Z_2</span> калибровочное поле, в то время как оставшийся подвижный фермион распространяется в стационарном фоне этого поля, а возбуждение <span class="katex-eq" data-katex-display="false">Z_2</span> потока внутри гексагональной ячейки изменяет знак всех переменных, пересекаемых соответствующим оператором, что приводит к формированию дираковских конусов в основном состоянии при отсутствии возмущений, нарушающих симметрию относительно обращения времени. — В модели сотовой структуры с спин-орбитальной фрустрацией, локальные спиновые степени свободы расщепляются на четыре майорановских фермиона, образующих связанные пары и определяющие локальное $Z_2$ калибровочное поле, в то время как оставшийся подвижный фермион распространяется в стационарном фоне этого поля, а возбуждение $Z_2$ потока внутри гексагональной ячейки изменяет знак всех переменных, пересекаемых соответствующим оператором, что приводит к формированию дираковских конусов в основном состоянии при отсутствии возмущений, нарушающих симметрию относительно обращения времени.

Исследование феноменов, вызванных магнитным полем в спиновых жидкостях Китая, демонстрирует, как даже самые строгие теоретические модели нуждаются в постоянной проверке и уточнении. Подобно тому, как магнитное поле изменяет свойства спиновой жидкости, так и интерпретация данных требует критического подхода. Ведь каждая метрика — это идеология в disguise. Конфуций говорил: “Изучай прошлое, чтобы понимать настоящее, и предвидеть будущее.” В данном случае, понимание фазовых переходов, индуцированных магнитным полем, и поиск признаков квантового майорановского металла, требуют не только точных расчетов, но и осознания границ применимости этих самых расчетов. Если показатели роста наблюдаются, значит, кто-то неправильно измеряет. Эта работа подчеркивает, что истина рождается не из одной модели, а из последовательности проверок, ошибок и сомнений.

Что дальше?

Представленные теоретические и численные исследования, касающиеся явлений, индуцированных магнитным полем в китовской спиновой жидкости, не столько разрешают вопросы, сколько обнажают новые. Возникновение фазы «Майорановского металла» — любопытная гипотеза, но её экспериментальное подтверждение требует не просто регистрации сигнала, а демонстрации истинно топологической защиты, а не артефакта, замаскированного под неё. Нельзя забывать, что любое соответствие с теорией — лишь приглашение к сомнению, особенно когда речь идет о столь экзотических состояниях материи.

Переход к более низким измерениям, проявившийся под воздействием магнитного поля, — ещё одна область, требующая осторожности. Утверждения о «суб-дименсиональной динамике» звучат элегантно, но физика низкоразмерных систем полна неожиданностей и ловушек, где даже небольшие отклонения от идеальной модели могут кардинально изменить картину. Необходимо помнить: упрощение — это не всегда путь к пониманию, иногда это лишь удобный способ избежать сложных вопросов.

В конечном итоге, прогресс в этой области зависит не от создания всё более сложных моделей, а от разработки новых, принципиально иных методов экспериментальной проверки. Данные не лгут, но их интерпретация требует не только математической точности, но и критического мышления, способности признать собственные ошибки и сомнения. Истина рождается не из убеждений, а из последовательности проверок, ошибок и новых вопросов.

Оригинал статьи: https://arxiv.org/pdf/2601.14496.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-22 15:07