Магнитная симметрия треугольных решеток: как нарушить и восстановить

Автор: Денис Аветисян

Новое исследование раскрывает общие закономерности спонтанного нарушения четности в квантовых антиферромагнетиках на треугольной решетке и демонстрирует, как внешние магнитные поля могут восстановить симметрию.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал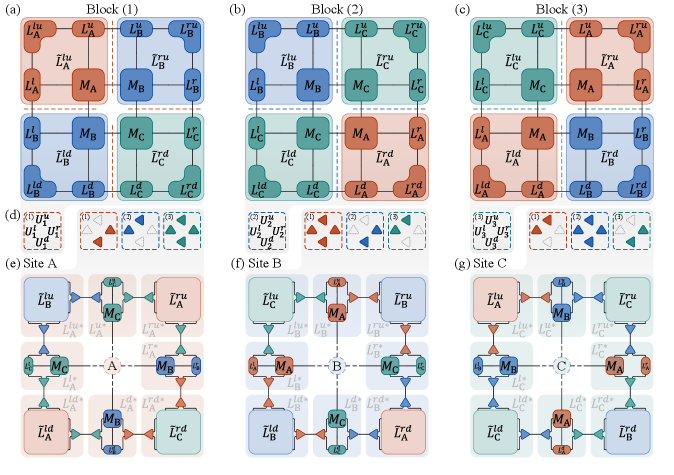

Процедура CTMRG для треугольной решетки предполагает последовательное обновление тензорных сред посредством сжатий с изометриями, полученными из сингулярного разложения на пунктирных разрезах, что позволяет ренормализовать краевые и угловые тензоры <span class="katex-eq" data-katex-display="false">L_{i}^{\mu}</span> и <span class="katex-eq" data-katex-display="false">L_{i}^{\mu\nu}</span>, составленными из локальных тензоров <span class="katex-eq" data-katex-display="false">M_{i}</span> и ассоциированных с ними тензоров связей. — Процедура CTMRG для треугольной решетки предполагает последовательное обновление тензорных сред посредством сжатий с изометриями, полученными из сингулярного разложения на пунктирных разрезах, что позволяет ренормализовать краевые и угловые тензоры $L_{i}^{\mu}$ и $L_{i}^{\mu\nu}$ , составленными из локальных тензоров $M_{i}$ и ассоциированных с ними тензоров связей.

Работа использует усовершенствованный метод CTMRG для изучения экзотических фаз, включая сверхтвердые состояния, и подтверждает, что увеличение магнитного поля обычно восстанавливает четность.

Фрустрированные системы на треугольной решетке традиционно представляют сложность в понимании их фазовых переходов и экзотических состояний. В работе ‘Spontaneous Parity Breaking in Quantum Antiferromagnets on the Triangular Lattice’ показано, что спонтанное нарушение четности играет ключевую роль в формировании этих фаз, определяя условия возникновения нетривиальных состояний, включая сверхтвердые тела. Установлено, что нарушение четности, как правило, восстанавливается при увеличении внешних магнитных полей, а предложенный подход, основанный на усовершенствованных методах CTMRG, позволяет подтвердить эти результаты. Можно ли использовать этот принцип для систематического анализа взаимодействия спина, симметрии и фрустрации в более широком классе многочастичных систем?

Геометрическая Фрустрация и Рождение Новых Магнитных Фаз

Квантовые спиновые системы, особенно те, что расположены на треугольных решетках, демонстрируют присущую им геометрическую фрустрацию, возникающую из-за конкурирующих взаимодействий между спинами. В подобных системах каждое спиновое взаимодействие стремится выровнять соседние спины определенным образом, однако геометрия решетки делает невозможным одновременное удовлетворение всех этих требований. Это приводит к тому, что система не может найти состояние с минимальной энергией, что и называется фрустрацией. В результате спины не упорядочиваются в традиционные магнитные фазы, а образуют сложные, нетривиальные конфигурации, способствуя возникновению экзотических квантовых явлений и новых магнитных состояний вещества. Данная фрустрация является фундаментальной причиной, определяющей уникальные свойства и поведение этих систем.

В квантовых спиновых системах, особенно на треугольных решетках, геометрическая фрустрация часто приводит к разрушению привычного магнитного порядка и появлению экзотических спиновых фаз. Вместо упорядоченного расположения спинов возникает ситуация, когда они не могут одновременно минимизировать свою энергию, что ведет к образованию сложных, нетривиальных состояний материи. Эти фазы характеризуются новыми коллективными возбуждениями и необычными магнитными свойствами, отличными от ферро- или антиферромагнетизма. Исследование этих состояний открывает возможности для создания новых материалов с уникальными характеристиками, например, для квантовых вычислений или спинтроники. Подобные системы представляют собой полигоны для изучения фундаментальных аспектов квантовой механики и коллективного поведения многих частиц.

Для полного понимания экзотических спиновых фаз, возникающих в квантовых системах, необходимо исследовать случаи нарушения симметрии четности — фундаментальной пространственной симметрии. Нарушение этой симметрии означает, что система ведет себя по-разному при отражении в пространстве, что приводит к появлению уникальных магнитных структур и новых квантовых состояний. Исследования показывают, что именно нарушение четности играет ключевую роль в стабилизации этих фаз и позволяет им проявляться даже при наличии сильной геометрической фрустрации. Изучение систем с нарушенной симметрией четности открывает путь к созданию новых материалов с необычными магнитными свойствами и потенциальными применениями в квантовых технологиях.

Взаимодействие между геометрической фрустрацией и нарушением чётности играет решающую роль в возникновении новых квантовых явлений в спиновых системах. Недавние исследования продемонстрировали существование чёткого правила, управляющего этим нарушением чётности, что позволяет предсказывать и контролировать возникновение экзотических магнитных фаз. В частности, обнаружено, что специфические конфигурации спинов, обусловленные фрустрацией, приводят к спонтанному нарушению чётности, проявляющемуся в асимметричном распределении магнитных моментов. Это нарушение не только открывает путь к созданию материалов с уникальными свойствами, но и углубляет понимание фундаментальных принципов, лежащих в основе квантового магнетизма. $\vec{S}_i \cdot (\vec{S}_j \times \vec{S}_k)$ — подобное взаимодействие является ключевым фактором, определяющим нарушение чётности в исследуемых системах.

Фазовые диаграммы основного состояния модели TLXXZ для спина <span class="katex-eq" data-katex-display="false">S=1/2, 1</span> и <span class="katex-eq" data-katex-display="false">5/2</span> демонстрируют различные магнитные фазы (FM, Umbrella, V, Y, UUD) на подрешетках AA, BB и CC, разделенные линиями, обозначающими фазовые переходы с изменением четности. — Фазовые диаграммы основного состояния модели TLXXZ для спина $S=1/2, 1$ и $5/2$ демонстрируют различные магнитные фазы (FM, Umbrella, V, Y, UUD) на подрешетках AA, BB и CC, разделенные линиями, обозначающими фазовые переходы с изменением четности.

Экзотические Спиновые Фазы и Их Конфигурации

Модель TLXXZ, включающая продольное магнитное поле и анизотропию, представляет собой эффективную платформу для исследования экзотических спиновых фаз. В данной модели взаимодействие между спинами описывается гамильтонианом, учитывающим как обменные взаимодействия, так и влияние внешнего магнитного поля, направленного вдоль одной из координатных осей, и анизотропного взаимодействия, которое предпочитает определенную ориентацию спинов. Комбинация этих факторов приводит к возникновению сложных магнитных структур и фазовых переходов, которые трудно исследовать в более простых моделях. Параметры модели — величина магнитного поля, сила анизотропии и обменные константы — позволяют тонко настраивать магнитное поведение системы и получать разнообразные спиновые конфигурации, необходимые для изучения фундаментальных свойств магнитных материалов.

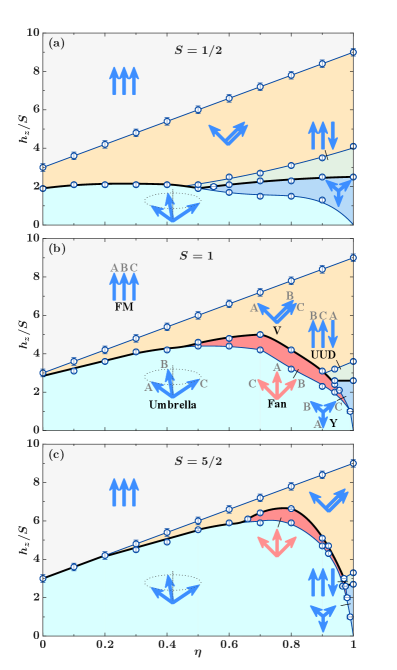
Модель TLXXZ допускает существование нескольких различных спиновых конфигураций, включая фазы ‘Веер’, ‘V-образная’ и ‘Зонтичная’. В фазе ‘Веер’ спины выстраиваются последовательно, образуя структуру, напоминающую веер. ‘V-образная’ фаза характеризуется спинами, направленными в противоположные стороны, формируя V-образную структуру. В ‘Зонтичной’ фазе спины сходятся к центральной точке, отклоняясь в стороны, подобно раскрытому зонтику. Каждая из этих фаз отличается уникальным расположением спинов и определяется конкретным сочетанием параметров модели, таких как величина магнитного поля и анизотропии.

Фазовые переходы в магнитных системах, такие как образование ‘Fan’, ‘V-образной’ и ‘Зонтичной’ конфигураций спинов, обусловлены сложным взаимодействием между фрустрацией, внешним магнитным полем и спонтанным нарушением симметрии четности. Фрустрация возникает из-за конкурирующих магнитных взаимодействий, препятствующих установлению упорядоченного состояния. Применение магнитного поля снимает некоторые ограничения, вызванные фрустрацией, и способствует формированию нетривиальных магнитных структур. Нарушение симметрии четности приводит к возникновению спонтанной намагниченности и определяет асимметричный характер спиновых конфигураций. Комбинация этих факторов определяет стабильность и свойства экзотических магнитных фаз.

Применение магнитного поля в модели TLXXZ приводит к появлению спиновых конфигураций, не сохраняющих симметрию относительно инверсии. В отсутствие поля система может демонстрировать состояния с четкой симметрией относительно изменения направления спинов на противоположное. Однако внешнее магнитное поле снимает это ограничение, позволяя формироваться асимметричным фазам, таким как ‘Fan’, ‘V-Shaped’ и ‘Umbrella’. Это происходит из-за нарушения баланса между энергиями различных спиновых состояний под воздействием поля, что приводит к предпочтительному выстраиванию спинов в определенном направлении и формированию несимметричных структур. $H$ — величина магнитного поля, влияющая на стабильность этих фаз.

Исследование намагниченности <span class="katex-eq" data-katex-display="false">M_z</span> в бислойной модели TLXXZ при различных значениях <span class="katex-eq" data-katex-display="false">h_z</span> показало, что конфигурации спинов, характеризуемые количеством синглетов (S) и триплетов (T), а также сохранением четностей a и b, определяют фазовое поведение системы, как это показано на иллюстрации структуры решетки и типичных спиновых конфигурациях. — Исследование намагниченности $M_z$ в бислойной модели TLXXZ при различных значениях $h_z$ показало, что конфигурации спинов, характеризуемые количеством синглетов (S) и триплетов (T), а также сохранением четностей a и b, определяют фазовое поведение системы, как это показано на иллюстрации структуры решетки и типичных спиновых конфигурациях.

Двуслойные Системы и Возникновение Димеризации

Переход к двуслойной модели TLXXZ вводит взаимодействия между слоями, что значительно усложняет фазовую диаграмму системы. Введение межслойных взаимодействий позволяет исследовать новые фазы и состояния, недоступные в однослойных моделях. Эти взаимодействия влияют на энергетический ландшафт системы, изменяя стабильность различных магнитных упорядочений и способствуя появлению новых типов коллективных состояний. Анализ фазовой диаграммы двуслойной модели требует учета как внутрислойных, так и межслойных параметров взаимодействия для полного понимания ее свойств и предсказания возможных магнитных фаз.

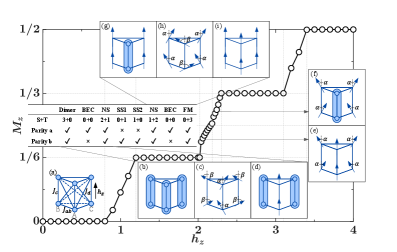
Модель TLXXZ в бислойном варианте демонстрирует склонность к димеризации, процессу, при котором спины объединяются в пары. Формирование этих пар приводит к снижению общей намагниченности системы, поскольку спины, входящие в димеры, компенсируют друг друга. В отличие от ферромагнитных состояний, где спины выстраиваются параллельно, димеризация способствует образованию антиферромагнитных корреляций внутри димеров, уменьшая макроскопическую намагниченность и изменяя магнитные свойства материала. Данный эффект является ключевым для понимания формирования новых коррелированных электронных состояний в бислойных системах.

В системах с конкурирующими взаимодействиями, таких как модели с фрустрацией, возникает тенденция к димеризации, приводящая к образованию как синглетных состояний с нулевым полным спином $S = 0$ , так и триплетных состояний с полным спином, равным единице $S = 1$ . Образование синглетных состояний связано с антиферромагнитным упорядочением спинов в парах, минимизирующим энергию системы. При этом наличие фрустрации препятствует полному упорядочению спинов, что способствует стабильности триплетных состояний и коэксистенции обоих типов состояний в фазовой диаграмме. Соотношение между синглетными и триплетными состояниями зависит от параметров взаимодействия и может быть исследовано с помощью численных методов, таких как тензорные сети.

Численное моделирование системы на основе модели TLXXZ с учетом межслоевых взаимодействий проводилось с использованием метода CTMRG с виртуальной размерностью связи 4 и размерностью усечения 48. Для стабилизации межслоевой димеризации и формирования димеров использовались параметры обменного взаимодействия: $J_{ab} = 0.425$ , $J_c = 1$ и $J_d = 0.325$ . Полученные результаты позволяют исследовать механизмы формирования новых коррелированных электронных состояний, в частности, связанных с образованием димерных структур и изменением магнитных свойств материала.

Валидация Расчетами: Метод Ренормализационной Группы на основе Матрицы Углового Переноса

Метод ренормализационной группы на основе матрицы углового переноса (CTMRG) представляет собой мощный вычислительный подход к моделированию поведения спиновых систем. CTMRG позволяет эффективно рассчитывать свойства систем, сводя многочастичную задачу к последовательному решению для блоков меньшего размера с последующей экстраполяцией к термодинамическому пределу. Этот метод особенно эффективен для исследования систем с сильными корреляциями и фрустрациями, где традиционные методы сталкиваются с трудностями. Ключевым аспектом CTMRG является использование тензорных сетей для представления волновой функции, что позволяет контролировать экспоненциальный рост вычислительных затрат и достигать высокой точности в расчетах.

Метод Corner-Transfer-Matrix Renormalization Group (CTMRG) позволяет проводить крупномасштабное моделирование моделей TLXXZ и двуслойных TLXXZ, что обеспечивает точные прогнозы их фазовых диаграмм. Эффективность CTMRG обусловлена его способностью обрабатывать тензорные сети высокой размерности, возникающие при описании этих систем. Вычислительные возможности метода позволяют исследовать системы с большим числом спинов и определять границы между различными магнитными фазами, такими как ферромагнитные, антиферромагнитные и спиновые жидкости. Точность предсказаний фазовых диаграмм, полученных с помощью CTMRG, подтверждается сравнением с результатами, полученными другими численными методами и аналитическими подходами.

Использование алгоритма Corner-Transfer-Matrix Renormalization Group (CTMRG) позволило исследователям подтвердить существование предсказанных спиновых фаз в TLXXZ и двуслойных TLXXZ моделях, а также детально изучить их свойства. В ходе вычислений была достигнута энергия основного состояния, равная -0.1824, что соответствует результатам, полученным другими CTMRG-ориентированными подходами. Данное соответствие подтверждает надежность и точность CTMRG как инструмента для анализа квантовых спиновых систем и верификации теоретических предсказаний относительно их фазовых диаграмм.

Метод Corner-Transfer-Matrix Renormalization Group (CTMRG) особенно эффективен при исследовании систем с фрустрированными взаимодействиями, поскольку способен адекватно учитывать сложные корреляции между спинами. Фрустрация возникает, когда система не может одновременно минимизировать энергию всех взаимодействий, что приводит к появлению множества вырожденных состояний и нетривиальному поведению. CTMRG позволяет моделировать эти системы, численно решая задачу о наземном состоянии и определяя фазовые диаграммы, что затруднительно для традиционных методов, особенно при увеличении размера системы и сложности взаимодействий. Способность CTMRG эффективно обрабатывать сложные спиновые взаимодействия делает его незаменимым инструментом для изучения фундаментальных свойств магнитных материалов с фрустрированными связями.

К Сверхтвердым Фазам и За Ее Пределами

Взаимодействие между нарушенной чётностью и коррелированными спиновыми состояниями открывает захватывающие перспективы для обнаружения совершенно новых фаз материи. Исследования показывают, что нарушение симметрии чётности, когда система перестает быть инвариантной относительно зеркального отражения, в сочетании с сильными взаимодействиями между спинами электронов, может приводить к возникновению экзотических состояний, не имеющих классических аналогов. Эти состояния характеризуются необычными свойствами, такими как топологические дефекты и квазичастицы с фракционированными статистиками, что потенциально может быть использовано в квантовых технологиях. Нарушение чётности создает основу для формирования новых коллективных мод, а коррелированные спины обеспечивают механизм для стабилизации этих мод и формирования упорядоченных структур, существенно отличающихся от привычных кристаллических решеток.

Взаимодействие между нарушенной чётностью симметрии и коррелированными спиновыми состояниями может приводить к возникновению так называемых сверхтвёрдых фаз вещества. Эти уникальные состояния материи демонстрируют одновременное сочетание свойств кристаллов — упорядоченной структуры — и сверхтекучестей, позволяя веществу течь без вязкости, сохраняя при этом жесткость. Представьте себе материал, способный одновременно выдерживать механические нагрузки и протекать сквозь узкие каналы без сопротивления — именно такие необычные характеристики присущи сверхтвёрдым фазам. Изучение этих фаз представляет значительный интерес для физики конденсированного состояния, поскольку они открывают новые возможности для создания материалов с принципиально новыми свойствами и потенциальными применениями в различных областях науки и техники.

Понимание фаз сверхтекучего твердого тела открывает широкие перспективы для создания принципиально новых квантовых материалов. Эти материалы, сочетающие в себе свойства кристаллов и сверхтекучих жидкостей, могут обладать уникальными характеристиками, такими как нулевое сопротивление и способность к квантовой проводимости. Исследователи полагают, что манипулирование этими фазами позволит создавать устройства нового поколения — от сверхчувствительных сенсоров и квантовых компьютеров до эффективных накопителей энергии и сверхпроводящих линий передачи. Более того, изучение механизмов возникновения этих фаз углубляет фундаментальное понимание коллективного поведения квантовых частиц, что, в свою очередь, способствует разработке материалов с заданными свойствами и открывает путь к технологическим прорывам в различных областях науки и техники.

Исследования фрустрированных систем, характеризующихся конфликтующими взаимодействиями между составляющими элементами, открывают перспективы для обнаружения совершенно новых квантовых явлений. В таких системах, где обычные принципы упорядочения не работают, возникают экзотические состояния материи, не подчиняющиеся классическим представлениям. Углубленное изучение этих систем предполагает не только расширение фундаментальных знаний о квантовой механике и фазовых переходах, но и потенциальную возможность создания материалов с уникальными и непредсказуемыми свойствами, способными революционизировать различные области науки и техники. Ожидается, что дальнейшие исследования позволят выявить ранее неизвестные формы квантовой запутанности и корреляций, что, в свою очередь, углубит понимание основополагающих законов природы и откроет путь к разработке принципиально новых квантовых технологий.

Исследование демонстрирует, что даже в кажущемся хаосе фрустрированных систем, таких как треугольная решетка, существуют фундаментальные правила, определяющие поведение материи. Авторы показывают, как внешнее магнитное поле может восстановить симметрию, нарушенную внутренними взаимодействиями. Этот процесс, детально изученный с помощью усовершенствованного метода CTMRG, подчеркивает важность последовательной проверки гипотез и сомнения в первоначальных ожиданиях. Ведь, как говорил Конфуций: «Не тот умен, кто знает много, а тот, кто умеет отличать истинное от ложного». Подтверждение этих принципов, особенно в контексте экзотических фаз вроде сверхтекучих твердых тел, требует не только вычислительной точности, но и интеллектуальной строгости.

Куда двигаться дальше?

Представленные результаты, безусловно, проливают свет на сложную связь между магнитным полем и нарушением чётности в тригональных антиферромагнетиках. Однако, говорить о полном понимании было бы преждевременно. Каждый полученный «фазовый переход» — это лишь подтверждение текущих моделей, а не доказательство их абсолютной истинности. Показатели, конечно, растут, но не стоит забывать, что растут они и тогда, когда кто-то меняет способ измерения.

Перспективным направлением представляется расширение исследований за пределы идеализированных тригональных решёток. Реальные материалы всегда содержат дефекты и отклонения от совершенства, которые могут существенно влиять на наблюдаемые фазы. Игнорирование этих факторов — это, мягко говоря, упрощение. Кроме того, необходимо более глубокое понимание динамических свойств этих систем. Статические расчеты дают лишь снимок момента, в то время как физика проявляется в движении.

Наконец, стоит признать, что концепция «экзотических фаз», таких как сверхтвердые тела, требует более строгих критериев определения. Нельзя просто назвать что-то «необычным» и считать задачу решенной. Истинное понимание приходит не от поиска новых названий для старых явлений, а от способности предсказывать поведение системы в новых условиях. Иначе, все эти «фазы» останутся лишь математическими химерами.

Оригинал статьи: https://arxiv.org/pdf/2602.05901.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-06 20:03