Автор: Денис Аветисян
В статье представлена общая теоретическая база для описания систем, демонстрирующих мезоскопические флуктуации, и их влияние на термодинамические свойства материалов.
Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.
Бесплатный телеграм-канал
Исследование посвящено анализу мезоскопических флуктуаций в статистических системах, включая гетерофазные системы и термодинамические потенциалы.
В статистической физике часто возникает противоречие между макроскопическим описанием систем и локальными флуктуациями, размер которых сопоставим с межатомными расстояниями. Настоящая работа, посвященная исследованию ‘Mesoscopic Fluctuations in Statistical Systems’, рассматривает флуктуации мезоскопического масштаба, существенно превышающие среднее расстояние между ближайшими частицами, но значительно уступающие размеру всей системы. Предлагается общий теоретический подход к описанию этих флуктуаций, рассматриваемых как локальные изменения фазового состояния внутри основной фазы, и анализируется их влияние на термодинамические свойства и фазовые переходы в различных материалах и системах. Каким образом учет мезоскопических флуктуаций может расширить наше понимание неравновесных процессов и критических явлений в конденсированных средах и сложных системах?
Фундамент: Статистические системы и фазовое пространство
Изучение поведения сложных материалов начинается с определения лежащей в основе статистической системы и множества её возможных состояний, описываемых посредством фазового пространства. Это пространство представляет собой многомерное поле, где каждая точка соответствует уникальной конфигурации системы — положению всех её компонентов. Понимание структуры этого пространства критически важно, поскольку именно в нем определяются все возможные пути эволюции материала. Анализ фазового пространства позволяет выявить закономерности, предсказать реакцию материала на внешние воздействия и, в конечном итоге, разработать новые материалы с заданными свойствами. Рассмотрение системы как совокупности вероятных состояний в фазовом пространстве позволяет перейти от описания отдельных частиц к макроскопическому поведению материала, что является ключевым для понимания его свойств.
В основе изучения сложных материалов лежит понятие вероятностного распределения, которое определяет, с какой вероятностью система окажется в том или ином состоянии. Данное распределение, по сути, является картой, показывающей наиболее вероятные конфигурации системы в многомерном фазовом пространстве. Именно оно позволяет предсказывать макроскопические свойства материала, исходя из поведения его микроскопических компонентов. P(q_i), где q_i — координаты в фазовом пространстве, описывает вероятность обнаружения системы в определенной точке этого пространства. Понимание формы и характеристик этого распределения — ключевой фактор для анализа динамики и равновесных свойств сложных систем, позволяющий выявить закономерности и предсказать их поведение в различных условиях.
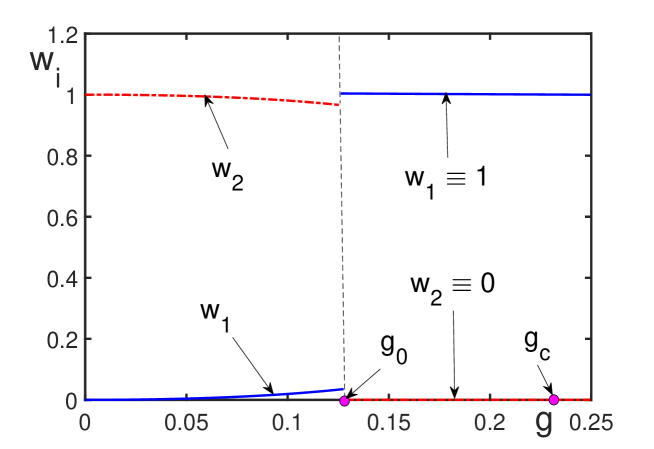
Пространство Гильберта служит фундаментальной математической основой для описания состояний сложных систем, обеспечивая возможность строгого анализа их динамики. Это абстрактное векторное пространство позволяет представлять все возможные состояния системы в виде векторов, что облегчает применение математических инструментов для изучения эволюции системы во времени. В частности, исследования показали, что фаза фрустрированных материалов, характеризующаяся конкуренцией между различными взаимодействиями, существует вплоть до значения параметра фрустрации, равного 0.231632. Этот предел указывает на границу стабильности данной фазы и может служить отправной точкой для дальнейших исследований, направленных на понимание поведения материалов в условиях сильной фрустрации и поиск новых материалов с необычными свойствами.
Взвешенные и волокнистые пространства: Расширяя границы моделей
Для моделирования систем, в которых определенные состояния обладают большей вероятностью, вводятся понятия Взвешенного фазового пространства (WeightedPhaseSpace) и Взвешенного гильбертова пространства (WeightedHilbertSpace). В этих пространствах каждому состоянию присваивается вес, который напрямую влияет на расчеты вероятностей и ожидаемых значений. Вес w_i состояния |\psi_i\rangle в взвешенном гильбертовом пространстве используется при вычислении скалярного произведения: \langle \psi_j | \psi_i \rangle \rightarrow w_i \langle \psi_j | \psi_i \rangle. Это позволяет учитывать априорные знания о системе и моделировать неравновесные процессы или системы с несимметричным распределением вероятностей. Взвешивание эффективно изменяет метрику пространства состояний, делая более вероятные состояния более «значимыми» при расчете физических величин.
При описании систем, демонстрирующих несколько термодинамических фаз, FiberedHilbertSpace предоставляет эффективный подход, объединяя множественные гильбертовы пространства в единое представление. Этот подход позволяет рассматривать каждую фазу как отдельное гильбертово пространство H_i, а FiberedHilbertSpace формируется как объединение этих пространств H = \bigcup H_i. Такая конструкция позволяет учитывать различия в квантовых состояниях, существующих в различных фазах, и корректно описывать системы с комплексными фазовыми границами, что особенно важно при моделировании свойств материалов и фазовых переходов.
Использование FiberedHilbertSpace позволяет эффективно описывать системы со сложной внутренней структурой и фазовыми границами, что критически важно для понимания свойств материалов. Данный подход позволяет представить систему как объединение нескольких гильбертовых пространств, каждое из которых соответствует определенной фазе или внутренней структуре. Это особенно актуально при исследовании материалов, демонстрирующих полиморфизм, фазовые переходы или сложные кристаллические структуры. Анализ поведения системы в рамках FiberedHilbertSpace позволяет учитывать влияние различных фаз и их взаимодействий на макроскопические свойства материала, такие как теплопроводность, механическая прочность и оптические характеристики. \Psi = \bigoplus_{i} H_i — общая волновая функция системы, представляющая собой прямую сумму гильбертовых пространств H_i , соответствующих различным фазам.
Эффективные гамильтонианы и кваверажные: Упрощая сложность
Эффективный гамильтониан представляет собой метод упрощения анализа сложных взаимодействий в физических системах путем усреднения по определенным степеням свободы. Этот подход позволяет исключить из рассмотрения несущественные для конкретной задачи переменные, концентрируясь на наиболее значимых факторах, определяющих поведение системы. В результате получается упрощенная модель, описывающая только релевантные взаимодействия, что существенно облегчает расчеты и позволяет получить приближенные, но зачастую достаточно точные результаты. Использование эффективного гамильтониана особенно полезно при исследовании систем со многими взаимодействующими частицами, где учет всех степеней свободы был бы вычислительно невозможен.
Метод кваверажних величин (Quasiaverage method) применяется для вычисления свойств в упрощенной модели эффективного гамильтониана. В его основе лежит использование взвешенных функций, позволяющих захватить существенные характеристики системы, игнорируя менее значимые детали. Эти функции определяются таким образом, чтобы отразить вклад различных степеней свободы в итоговый результат, обеспечивая приближение к фактическим значениям свойств системы при значительном снижении вычислительной сложности. Взвешивание производится с учетом времени жизни флуктуаций, что позволяет адекватно учитывать динамические эффекты и получать корректные оценки наблюдаемых величин.
Методы эффективных гамильтонианов и кваверажных позволяют моделировать флуктуации в системах конденсированного состояния с временами жизни в диапазоне от 10^{-{14}} с до 10^{-{12}} с. Локальное равновесие в таких системах, определяемое временем установления равновесия между взаимодействующими степенями свободы, обычно наблюдается приблизительно на отметке 10^{-{13}} с. Данный временной масштаб определяет применимость этих методов для исследования динамических процессов, происходящих на пикосекундных временных масштабах, и позволяет эффективно описывать системы, находящиеся в квазиравновесном состоянии.
Мезоскопические флуктуации и проявления в материалах: Порядок из хаоса
Мезоскопические флуктуации, проявляющиеся в промежуточных масштабах, оказывают существенное влияние на поведение различных материалов и определяют их свойства и реакцию на внешние воздействия. Эти флуктуации — отклонения от среднего состояния, возникающие из-за конечного размера исследуемых систем — не являются просто случайным шумом, а представляют собой фундаментальный аспект материальной организации. Они проявляются в виде локальных изменений порядка, концентрации или энергии, которые, хотя и кратковременны, способны существенно изменять макроскопические характеристики вещества. Например, в материалах с фазовыми переходами эти флуктуации могут предвещать возникновение новой фазы или влиять на скорость и механизм этого перехода. Понимание природы и масштабов мезоскопических флуктуаций необходимо для точного описания свойств материалов и разработки новых технологий, использующих эти явления.
Мезоскопические флуктуации проявляются в различных материалах, таких как магнитные, сегнетоэлектрические и сверхпроводящие, раскрывая фундаментальные механизмы, определяющие их уникальные свойства. В частности, в сверхпроводниках наблюдается повышение критической температуры, связанное с этими флуктуациями — отклонения от идеального состояния, которые, вопреки интуиции, способствуют более эффективному возникновению сверхпроводимости. Эти колебания, происходящие на нано- и микроуровне, создают временные пары куперовских электронов даже при температурах, близких к критической, тем самым облегчая переход в сверхпроводящее состояние и увеличивая температурный порог, при котором этот эффект проявляется. Изучение этих флуктуаций позволяет глубже понять природу сверхпроводимости и разрабатывать новые материалы с улучшенными характеристиками.
Понимание мезоскопических флуктуаций имеет решающее значение для целенаправленного проектирования и создания материалов с заданными свойствами для конкретных применений. Исследование этих флуктуаций позволяет не просто наблюдать, но и активно влиять на характеристики материалов, таких как сверхпроводники, сегнетоэлектрики и магнитные материалы. Контролируя эти колебания на мезоскопическом уровне, ученые получают возможность оптимизировать критические температуры в сверхпроводниках, повышать эффективность сегнетоэлектрических устройств и создавать магнитные материалы с улучшенными характеристиками. Таким образом, углубленное изучение флуктуаций открывает путь к разработке новых материалов с уникальными свойствами, востребованными в различных областях науки и техники, от энергетики и электроники до медицины и нанотехнологий.
Исследование мезоскопических флуктуаций, представленное в данной работе, раскрывает глубокую взаимосвязь между статистическими ансамблями и термодинамическими потенциалами. Развиваемый теоретический аппарат позволяет рассматривать системы, в которых флуктуации оказывают существенное влияние на фазовые переходы и свойства гетерофазных систем. Как некогда заметила Ханна Арендт: «Политическое пространство возникает там, где люди объединяются для действия, а не просто сосуществуют». Аналогично, в исследуемых системах, именно взаимодействие флуктуаций и ансамблевых свойств создает новое «пространство» для проявления термодинамических эффектов. Масштабируемость подобных моделей без учета этических аспектов интерпретации статистических данных может привести к искажению понимания реальных физических процессов, ускоряя движение к хаосу в научном познании.
Куда Ведёт Нас Мезоскопический Шум?
Представленная работа, стремясь описать мезоскопические флуктуации в статистических системах, неизбежно сталкивается с вопросом: достаточно ли простого описания для понимания реальных процессов? Развитие формализма, оперирующего квариусреднениями и взвешенными гильбертовыми пространствами, может привести к элегантным решениям, но существует риск, что подобная математическая красота заслонит физическую суть. Эффективность без понимания механизмов — иллюзия, особенно когда речь идёт о фазовых переходах в гетерофазных системах.
Дальнейшие исследования должны быть направлены не только на усовершенствование теоретического аппарата, но и на критическую оценку его применимости к конкретным материалам и системам. Необходимо учитывать, что мезоскопические флуктуации — это не просто шум, а потенциальный источник новых физических явлений, которые могут оказаться ключевыми для создания принципиально новых технологий. Однако, стремление к техническому прогрессу не должно подменять собой этическую ответственность за создаваемые инструменты.
В конечном счёте, истинный вызов заключается в том, чтобы преодолеть разрыв между абстрактными математическими моделями и сложной реальностью. Прогресс без этики — это ускорение без направления. Необходимо помнить, что каждый алгоритм кодирует определённое мировоззрение, и мы несём ответственность за ценности, которые автоматизируем.
Оригинал статьи: https://arxiv.org/pdf/2601.15782.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Все рецепты культистского круга в Escape from Tarkov
- Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip
- Решение головоломки с паролем Absolum в Yeldrim.
- Лучшие транспортные средства в Far Cry 6
- Лучшие шаблоны дивизий в Hearts Of Iron 4
- Необходимо: Как выращивать урожай
- Где найти и поймать бабочку Солнечного луча в Палии
- Dragon’s Dogma 2: Где найти Драконорожденных
- Как получить скины Alloyed Collective в Risk of Rain 2
- Warhorse говорит, что им пришлось отказаться от исторической точности для системы преступлений в Kingdom Come: Deliverance, так как это было бы ‘слишком сурово’ для ‘крестьянского парня’ Генри – ‘Любое преступление каралось бы очень строго’.
2026-01-25 23:46