На вершине потенциала: случайный отбор в бистабильных системах

Автор: Денис Аветисян

---

Новое исследование показывает, что бистабильные системы, инициализированные вблизи потенциального барьера, демонстрируют поведение, аналогичное распределению Больцмана, открывая возможности для принципиально новых подходов к вычислениям.

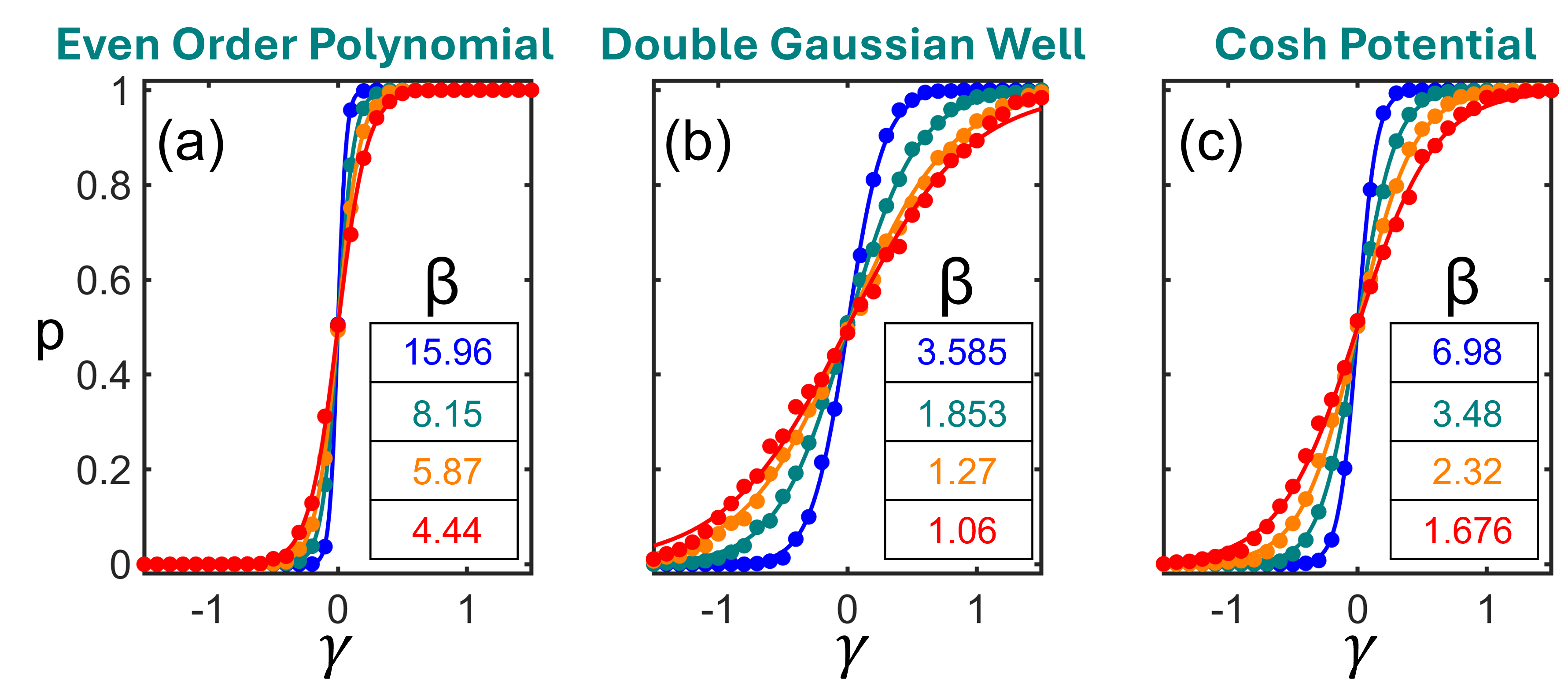
Работа раскрывает универсальный механизм стохастического отбора в системах с двойной ямой, демонстрируя связь с градиентными потоками и открывая путь к синхронным вычислениям, основанным на шуме.

Несмотря на успех транзисторов в цифровых вычислениях, поиск аппаратного примитива для вероятностных вычислений остается актуальной задачей. В работе, озаглавленной ‘At the Top of the Mountain, the World can Look Boltzmann-Like: Sampling Dynamics of Noisy Double-Well Systems’, исследуется универсальный механизм стохастического семплирования в бистабильных системах. Показано, что любой двухубый потенциал, при инициализации вблизи вершины барьера, демонстрирует поведение, аналогичное распределению Больцмана, обеспечивая основу для новой синхронной парадигмы вычислений. Какие перспективы открывает предложенный подход для создания эффективных и масштабируемых p-битов и вероятностных вычислительных систем?

---

Стохастические Основы: За Пределами Детерминированных Вычислений

Традиционные вычисления, основанные на детерминированных битовых операциях, сталкиваются с принципиальными ограничениями при моделировании систем, в которых присутствует неотъемлемая неопределенность. В основе классических компьютеров лежит представление информации в виде четких, однозначных значений — 0 или 1. Однако, многие реальные явления, такие как квантовые процессы, турбулентность или даже биологические системы, характеризуются вероятностным поведением, которое сложно адекватно описать с помощью жестких, предопределенных значений. Попытки смоделировать эти системы в рамках детерминированной парадигмы требуют сложных аппроксимаций и приводят к потере информации о присущей им вариативности. Это затрудняет создание точных прогнозов и ограничивает возможности анализа сложных систем, где случайность играет ключевую роль. Таким образом, существующие вычислительные методы оказываются недостаточно эффективными для задач, требующих учета и обработки неопределенности.

Стохастические вычисления, использующие вероятностные биты, представляют собой естественную основу для моделирования и обработки неопределенности и сложных систем. В отличие от традиционных вычислений, оперирующих с определенными значениями, данный подход позволяет представлять информацию в виде вероятностных распределений. Это особенно важно при работе с данными, содержащими шум или неполноту, а также при моделировании процессов, подверженных случайным воздействиям. Использование вероятностных битов позволяет эффективно представлять сложные взаимосвязи и зависимости, что находит применение в различных областях, включая машинное обучение, обработку сигналов и моделирование физических явлений. Вместо точного вычисления одного значения, стохастические вычисления оперируют с множеством возможных значений, взвешенных в соответствии с их вероятностью, что обеспечивает более гибкий и реалистичный подход к решению задач.

Распределение Больцмана является краеугольным камнем для понимания и реализации вероятностного поведения в стохастических вычислительных системах. Это математическое описание определяет вероятность нахождения системы в определенном состоянии в зависимости от энергии этого состояния и температуры системы. В контексте стохастических вычислений, P(E) = \frac{e^{-E/kT}}{Z}, где P(E) — вероятность состояния с энергией E, k — постоянная Больцмана, T — температура, а Z — статистическая сумма, обеспечивающая нормировку распределения. Использование этого распределения позволяет моделировать неопределенность и случайность, присущие многим реальным процессам, и создавать вычислительные модели, способные эффективно работать с нечеткими данными и сложными системами, где точные вычисления затруднены или невозможны. Оно служит основой для создания алгоритмов, основанных на статистической выборке и вероятностном моделировании, открывая новые горизонты в области искусственного интеллекта и машинного обучения.

Переход от точных вычислений к статистической выборке открывает принципиально новые возможности в вычислительных стратегиях. Вместо стремления к абсолютному значению результата, системы, основанные на вероятностных битах, оперируют распределениями вероятностей, что позволяет эффективно моделировать сложные и неопределенные явления. Такой подход особенно ценен при решении задач, где входные данные зашумлены или неполны, а также в областях, требующих оценки рисков и принятия решений в условиях неопределенности. Вместо детерминированного поиска единственного ответа, система производит множество случайных образцов, позволяя получить статистически значимое решение, отражающее вероятностную природу исследуемого процесса. Это позволяет создавать алгоритмы, более устойчивые к ошибкам и способные адаптироваться к изменяющимся условиям, что особенно важно в таких областях, как машинное обучение, обработка сигналов и моделирование сложных систем.

Физическая Реализация Вероятностных Битов

Несколько материальных систем, включая КМОП двухустойчивые триггеры, сегнетоэлектрики и оксиды, демонстрирующие фазовые переходы, способны физически реализовывать вероятностные биты, используя энергетические ландшафты с двумя минимумами. В этих системах стабильные состояния разделены энергетическим барьером, что приводит к вероятностному переключению между состояниями под воздействием тепловых флуктуаций. Глубина потенциальных ям и высота барьера определяют вероятность пребывания в каждом состоянии и скорость переключения, что позволяет настраивать характеристики вероятностного бита. Такая реализация позволяет физически представить вероятностные значения, в отличие от программного моделирования.

В основе реализации вероятностных битов в различных материальных системах лежит использование случайных тепловых флуктуаций. Эти флуктуации приводят к вероятностному переходу между стабильными состояниями системы, что и позволяет моделировать поведение вероятностного бита. Интенсивность тепловых флуктуаций, а следовательно и скорость переходов между состояниями, зависит от температуры и характеристик энергетического ландшафта системы, определяя вероятность нахождения бита в каждом из состояний. Данный механизм позволяет создавать физические реализации p-битов, не требующие внешнего управляющего воздействия для изменения вероятности состояний.

Магнитно-туннельные переходы с низким барьером представляют собой перспективную реализацию вероятностных битов, поскольку позволяют регулировать скорость переключения состояний. В этих устройствах, вероятность туннелирования электронов через барьер экспоненциально зависит от его высоты и ширины, а также от температуры. Уменьшение высоты барьера и/или увеличение температуры увеличивает вероятность переключения, что позволяет контролировать распределение вероятностей между состояниями «0» и «1». Важно, что скорость переключения может быть точно настроена за счет изменения параметров барьера и приложенного напряжения, что критически важно для реализации различных вероятностных вычислений и алгоритмов.

Проектирование физических вероятностных битов (p-битов) неразрывно связано с пониманием и контролем лежащего в их основе энергетического ландшафта. Форма энергетической ямы, определяемая свойствами материала и архитектурой устройства, непосредственно влияет на вероятность переключения между стабильными состояниями. Глубина потенциальных ям и высота барьеров между ними определяют скорость и частоту спонтанных переключений, критичных для реализации вероятностных вычислений. Точное моделирование и манипулирование этим ландшафтом, включая контроль таких параметров как температура и приложенное поле, необходимо для достижения требуемых характеристик p-битов, таких как заданная вероятность состояния и стабильность.

Динамика Стохастического Переключения

Динамика переключения асинхронных p-битов описывается теорией Крамерса, определяющей скорость перехода через энергетический барьер. Скорость переключения экспоненциально зависит от высоты этого барьера V, что означает, что увеличение V приводит к существенному замедлению переключения. В рамках данной теории, вероятность переключения определяется как \Gamma \propto exp(-V/kT), где k — постоянная Больцмана, а T — абсолютная температура. Эффективная высота барьера может изменяться под влиянием различных факторов, включая приложенные поля и флуктуации, что необходимо учитывать при моделировании и оптимизации асинхронных схем.

Синхронный режим переключения в асинхронных p-битах достигается путем преодоления энергетического барьера, что предполагает подачу внешнего воздействия, способствующего переходу системы из одного стабильного состояния в другое. Одним из эффективных методов реализации данного подхода является использование второй гармоники (second-harmonic injection), которая обеспечивает необходимую энергию для преодоления барьера. Применение второй гармоники позволяет контролировать скорость переключения и обеспечивает предсказуемое поведение системы, в отличие от стохастических процессов, где переключение определяется вероятностью преодоления барьера за счет тепловых флуктуаций. Этот метод особенно важен для приложений, требующих детерминированного и быстрого переключения между состояниями.

Динамика градиентного потока обеспечивает теоретическую основу для анализа процесса релаксации системы к состоянию с минимальной энергией. В рамках данной модели, скорость релаксации пропорциональна градиенту потенциальной энергии и обратно пропорциональна коэффициенту трения или диссипации. Таким образом, система стремится к минимизации своей энергии, перемещаясь по направлению наиболее крутого спуска потенциальной поверхности. Анализ градиентного потока позволяет количественно оценить время релаксации и предсказать поведение системы вблизи энергетических минимумов, что особенно важно при исследовании переходов между стабильными состояниями и влиянии флуктуаций.

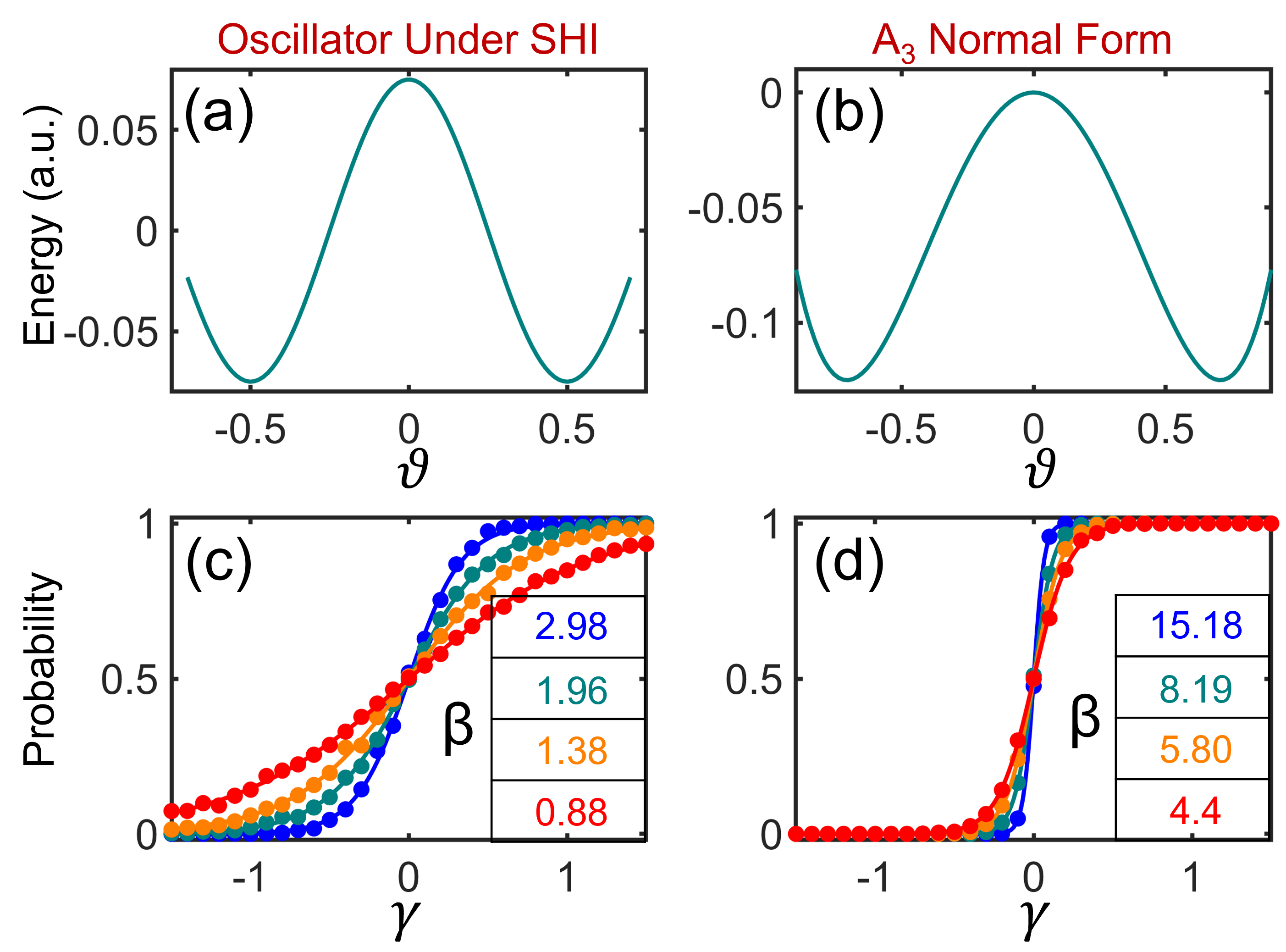
Нормальная форма A3 расширяет концепцию двухугольной энергетической поверхности, предоставляя упрощенное математическое описание динамики переключений. Среднее первое время прохождения (MFPT) рассчитывается как z_{th}/k_h в пределе низкого уровня шума и как z_{th}^2/(2Kn) в пределе высокого уровня шума. Данные выражения позволяют количественно оценить скорость переключения в зависимости от высоты барьера (z_{th}), его кривизны (k_h и K) и интенсивности шума, что обеспечивает основу для анализа и оптимизации систем стохастического переключения.

Влияние на Стохастические Вычисления

Колебательные контуры, подвергающиеся стохастической гармонической инъекции (SHI) и релаксационные генераторы, представляют собой перспективные физические реализации p-битов, использующие особенности двойного колодца потенциальной энергии. В основе этой концепции лежит способность этих систем переключаться между двумя стабильными состояниями, что соответствует логическим значениям 0 и 1 в вероятностном представлении. Двойной колодец обеспечивает энергетический ландшафт, где вероятность нахождения системы в каждом состоянии определяется энергией этого состояния, позволяя реализовывать вероятностные вычисления. Использование таких осцилляторов открывает путь к созданию энергоэффективных вычислительных архитектур, способных эффективно решать задачи, требующие вероятностного подхода и параллельной обработки информации, особенно в областях машинного обучения и оптимизации.

Среднее время первого прохождения (Mean First Passage Time, MFPT) играет ключевую роль в оценке эффективности выборки в синхронном режиме работы стохастических систем. Этот параметр определяет, насколько быстро система переходит из одного стабильного состояния в другое под воздействием случайных флуктуаций, что напрямую влияет на скорость и точность выполнения вычислений. Более короткое MFPT указывает на более быструю и эффективную выборку, позволяющую системе быстрее исследовать пространство состояний и достигать нужного результата. Исследования показывают, что оптимизация MFPT, например, путем изменения параметров потенциальной ямы или интенсивности шума, позволяет значительно повысить производительность стохастических вычислительных архитектур, особенно в задачах, требующих быстрого принятия решений в условиях неопределенности. Таким образом, точное измерение и контроль MFPT являются необходимыми условиями для разработки высокоэффективных и надежных систем стохастических вычислений.

Распределение Больцмана играет ключевую роль в разработке систем, использующих стохастическую выборку, особенно в условиях неопределенности. Проведенные исследования демонстрируют возможность достижения более чем 99% точности при использовании стохастической выборки, основанной на данном распределении. Результаты моделирования, проведенного для различных потенциальных функций с двойной ямой, полностью соответствуют теоретическим предсказаниям, что подтверждается высоким коэффициентом детерминации R^2 > 0.99. Это свидетельствует о надежности и эффективности предложенного подхода к реализации стохастических вычислений и открывает перспективы для создания энергоэффективных и устойчивых к помехам вычислительных архитектур.

Предложенная схема открывает перспективы для создания энергоэффективных и устойчивых архитектур стохастических вычислений. Использование физических осцилляторов, функционирующих в режиме стохастического переключения, позволяет существенно снизить энергопотребление по сравнению с традиционными вычислительными системами, где каждое логическое действие требует точного и гарантированного выполнения. Устойчивость данной архитектуры обеспечивается за счет внутренней способности системы к самокоррекции и адаптации к флуктуациям, что позволяет эффективно справляться с шумами и погрешностями. Такой подход не только минимизирует потребление энергии, но и повышает надежность вычислений, особенно в сложных и непредсказуемых условиях, создавая основу для нового поколения вычислительных устройств, способных эффективно решать задачи, требующие высокой степени вероятностного моделирования и обработки неопределенной информации.

Исследование демонстрирует, что даже в системах с двойной потенциальной ямой, инициализированных вблизи вершины барьера, наблюдается поведение, подобное распределению Больцмана. Этот универсальный механизм стохастической выборки открывает новые возможности для синхронных вычислений, где шум играет конструктивную роль. Как однажды заметил Пётр Капица: «В природе всё связано друг с другом, и нельзя рассматривать явления изолированно». Эта фраза отражает суть представленной работы, показывающей, как кажущийся хаос шума может привести к предсказуемому и полезному поведению в сложных системах, особенно когда речь идет о формировании энергетического ландшафта и его исследовании.

Куда Ведет Эта Тропа?

Представленные результаты, хотя и демонстрируют универсальность стохастического сэмплирования в бистабильных системах, не отменяют необходимости строгого математического анализа. Утверждение о “больцмановском” поведении требует не просто эмпирической проверки на тестовых потенциалах, но и доказательства сходимости к истинному распределению Больцмана в пределе. Очевидным ограничением является предположение об инициализации вблизи вершины барьера; какова чувствительность этого механизма к отклонениям от этого условия? Вопрос, требующий немедленного внимания.

Перспективы синхронных вычислений, основанных на этом принципе, кажутся заманчивыми, но требуют детальной проработки архитектуры. Понимание влияния шума, как источника вычислений, на надежность и точность результатов представляется ключевым. Очевидно, что не все задачи могут быть эффективно решены таким образом; необходимо определить класс проблем, для которых этот подход обеспечивает преимущество перед классическими алгоритмами. Иначе, мы рискуем построить элегантную, но бесполезную конструкцию.

В конечном счете, истинная ценность этой работы заключается в постановке вопроса о фундаментальной связи между стохастическими процессами и вычислительными возможностями. Следующим шагом должно стать развитие формальной теории, способной предсказывать и контролировать поведение таких систем, а не просто констатировать их “больцмановское” подобие. Иначе, это останется лишь красивой иллюстрацией, а не прочным фундаментом для новой парадигмы вычислений.

---

Оригинал статьи: https://arxiv.org/pdf/2602.04014.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

• Откровенные заметки, слитые стримером Lacari, привели к его бану на Twitch и Kick.

• Все рецепты культистского круга в Escape from Tarkov

• Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip

• Нечестивцам нет покоя: как получить старый ключ от коттеджа

• Решение головоломки с паролем Absolum в Yeldrim.

• Arknights: Endfield — Интерактивная карта (Долина IV)

• Акции UGLD. Южуралзолото ГК: прогноз акций.

• Прогнозы криптовалюты AXS: информация о ценах на AXS

• Лучшие шаблоны дивизий в Hearts Of Iron 4

• Кто такая Кселия Мендес-Джонс? 5 вещей, которые нужно знать об актере Fallout

2026-02-05 23:52