Автор: Денис Аветисян
Анализ данных, полученных космическим телескопом NICER, позволяет проверить альтернативные теории гравитации, выходящие за рамки общей теории относительности.
Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.
Бесплатный телеграм-канал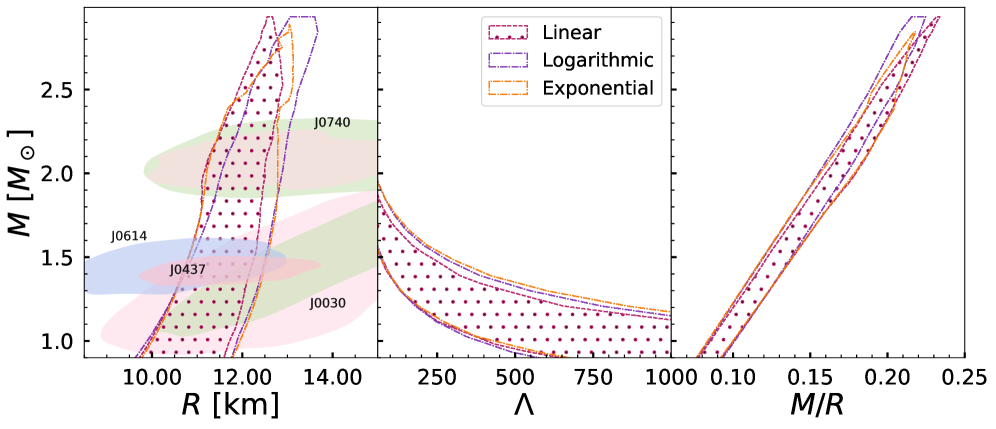
Байесовский анализ свойств нейтронных звезд в рамках f(Q)-гравитации показал, что экспоненциальная модель наиболее согласуется с наблюдательными данными.
Несмотря на успехи общей теории относительности, модификации гравитации остаются актуальным направлением исследований для объяснения космологических наблюдений. В работе ‘Bayesian Inference of Neutron Star Properties in $f(Q)$ Gravity Using NICER Observations’ проведено байесовское исследование свойств нейтронных звезд в рамках симметричной телепараллельной гравитации $f(Q)$, с использованием данных NICER. Полученные результаты указывают на статистическое предпочтение экспоненциальной модели $f(Q)$ по сравнению с линейной и логарифмической, при этом радиус и деформируемость при $1.4\,M_\odot$ составляют R_{1.4} = 11.27^{+0.53}_{-0.36}\,\mathrm{km} и \Lambda_{1.4} = 156.95^{+84.02}_{-{41}.73} соответственно. Может ли детальный анализ структуры нейтронных звезд стать ключевым инструментом для проверки альтернативных теорий гравитации в сильных гравитационных полях?
Исследование Пределов Гравитации: Вызов Нейтронных Звезд
Общая теория относительности, несмотря на свою выдающуюся успешность в описании гравитации, сталкивается с принципиальными трудностями при рассмотрении экстремальных гравитационных режимов. Вблизи сингулярностей, таких как черные дыры или в ядрах нейтронных звезд, предсказания теории становятся неопределенными, а математический аппарат — неспособным обеспечить корректные решения. Это связано с тем, что в этих условиях квантовые эффекты, игнорируемые в классической общей теории относительности, начинают играть существенную роль, требуя разработки новой, квантовой теории гравитации. Подобные ограничения указывают на необходимость поиска альтернативных теоретических подходов, способных адекватно описывать гравитацию в самых экстремальных условиях Вселенной, и объяснять наблюдаемые явления, которые не укладываются в рамки существующей модели. Исследование подобных границ применимости теории — ключевая задача современной физики.
Нейтронные звезды, представляющие собой самые плотные наблюдаемые объекты во Вселенной, служат уникальной лабораторией для проверки пределов применимости теории Эйнштейна. В их экстремальных условиях, где гравитация достигает невообразимых значений, проявляются эффекты, не наблюдаемые в обычных условиях. Изучение этих объектов позволяет ученым исследовать поведение материи при сверхвысоких плотностях и сильных гравитационных полях, что может выявить отклонения от предсказаний общей теории относительности. Именно вблизи поверхности нейтронных звезд, где гравитационное ускорение в миллиарды раз превышает земное, возникают условия для проверки фундаментальных принципов гравитации и поиска признаков новой физики, выходящей за рамки существующего понимания Вселенной. По сути, нейтронные звезды — это космические “гравитационные колодцы”, где можно наблюдать, как гравитация влияет на пространство и время в самых экстремальных проявлениях.
Точное определение зависимости массы от радиуса для нейтронных звезд является ключевой задачей современной астрофизики. Эта зависимость, связывающая массу звезды с её размером, позволяет проверить предсказания общей теории относительности в экстремальных условиях, существующих в недрах этих сверхплотных объектов. Однако, получение точных данных требует сочетания все более совершенных наблюдательных инструментов и сложных теоретических моделей, учитывающих поведение материи при невероятном давлении. Необходимость в повышении точности обусловлена тем, что текущие ограничения на зависимость масса-радиус допускают возможность существования альтернативных теорий гравитации, отличных от теории Эйнштейна, и дальнейшие исследования направлены на сужение этого диапазона неопределенности и проверку фундаментальных основ нашего понимания гравитации.
Несмотря на впечатляющие успехи общей теории относительности, современные наблюдательные данные о нейтронных звездах допускают возможность отклонений от предсказаний Эйнштейна. Существующие ограничения в точности измерений массы и радиуса этих сверхплотных объектов оставляют пространство для альтернативных теорий гравитации. Ученые активно исследуют модификации общей теории относительности, которые могли бы объяснить наблюдаемые характеристики нейтронных звезд, а также предсказать новые эффекты, которые могли бы быть обнаружены будущими наблюдениями. Это стимулирует развитие новых теоретических моделей и поиск более точных методов наблюдения, направленных на проверку фундаментальных основ гравитации в экстремальных условиях.
f(Q) Гравитация: Новый Геометрический Подход
Теория f(Q)-гравитации представляет собой модификацию общей теории относительности, вводя в рассмотрение понятие неметричности — геометрического свойства пространства-времени, описывающего изменение длины вектора при параллельном переносе. В общей теории относительности неметричность равна нулю, что соответствует метрической аффинности. В f(Q)-гравитации, неметричность рассматривается как динамическая величина, определяющая гравитационное взаимодействие, и описывается функцией f(Q) от скалярной неметричности Q. Введение неметричности позволяет изменить уравнения Эйнштейна и потенциально объяснить наблюдаемые космологические явления, такие как ускоренное расширение Вселенной, без необходимости введения дополнительных полей или измерений.
В отличие от многих других теорий модифицированной гравитации, f(Q)-гравитация потенциально способна решить космологические проблемы без введения дополнительных степеней свободы. Большинство альтернативных теорий, стремящихся объяснить темную энергию или темную материю, требуют добавления новых полей или измерений, что усложняет математический аппарат и может приводить к нефизическим предсказаниям. f(Q)-гравитация, модифицируя гравитационное действие через неметричность Q_\mu, позволяет изменять гравитационное взаимодействие, не вводя новых динамических переменных. Это означает, что количество степеней свободы остается равным двум, как и в общей теории относительности, что упрощает анализ стабильности и позволяет избежать некоторых проблем, связанных с дополнительными полями.
Различные модели гравитации f(Q) определяются конкретными функциональными формами, используемыми для выражения зависимости гравитационного поля от тензора неметричности Q_{\mu\nu}. Линейная модель f(Q) предполагает прямо пропорциональную связь между функцией f и Q, в то время как логарифмическая и экспоненциальная модели используют соответственно логарифмическую и экспоненциальную зависимости. Каждая из этих функциональных форм приводит к различным уравнениям поля и, следовательно, различным предсказаниям относительно космологической эволюции и гравитационных явлений, что делает выбор конкретной функциональной формы ключевым аспектом при построении и проверке моделей f(Q) гравитации.
В основе теории f(Q) гравитации лежит расширение общей теории относительности за счет введения понятия неметричности как геометрической характеристики пространства-времени. В то время как общая теория относительности описывает гравитацию посредством кривизны, а некоторые модифицированные теории гравитации — посредством кручения, f(Q) гравитация постулирует, что гравитационное взаимодействие может быть описано неметричностью Q_{\alpha\beta\gamma}, которая характеризует изменение длины векторных связей при параллельном переносе. Неметричность определяет, как меняется расстояние между точками при перемещении в пространстве-времени, и, таким образом, может влиять на геодезические линии и гравитационные эффекты. В f(Q) гравитации, гравитация определяется функционалом от неметричности f(Q), что позволяет строить различные модели в зависимости от выбора этого функционала.
Моделирование Нейтронных Звезд с Модифицированной Гравитацией
Уравнение Толмана-Оппенгеймера-Волкова (TOV) является фундаментальным инструментом для моделирования структуры нейтронных звезд, описывая гравитационный баланс внутри этих объектов. Решение этого уравнения требует использования уравнения состояния (EOS), которое связывает давление с плотностью вещества. Одним из примеров подходящего EOS является DDME2, представляющее собой нерелятивистское уравнение состояния, разработанное для описания ядерной материи при сверхвысоких плотностях. Комбинация уравнения TOV и EOS, такого как DDME2, позволяет рассчитывать профили массы и плотности внутри нейтронной звезды, определяя ее радиус и максимальную массу. \frac{dm}{dr} = 4\pi r^2 \rho(r) , где \rho(r) — плотность на радиусе r . Точность моделирования напрямую зависит от адекватности выбранного уравнения состояния для описания свойств плотной ядерной материи.
Применение уравнений Толмана-Оппенгеймера-Волкова совместно с уравнением состояния, например DDME2, в рамках f(Q)-гравитации позволяет численно рассчитывать массы и радиусы нейтронных звезд. Ф(Q)-гравитация модифицирует стандартную общую теорию относительности, вводя зависимость гравитационных полей от скалярного поля Q, что влияет на метрику пространства-времени внутри звезды. Решение уравнений гидростатического равновесия в этой модифицированной гравитации дает связь между массой звезды M и ее радиусом R. Полученные зависимости позволяют строить модели звезд различной массы и исследовать влияние модифицированной гравитации на их структуру и стабильность, что необходимо для сравнения с астрономическими наблюдениями.
Точные вычисления деформации приливными силами нейтронных звезд имеют критическое значение для сопоставления с данными, полученными при регистрации гравитационных волн. Деформация приливными силами, обозначаемая как Λ, характеризует степень искажения формы звезды под воздействием гравитационного поля другого объекта, например, второй нейтронной звезды или черной дыры в бинарной системе. Анализ формы гравитационных волн, возникающих при слиянии таких объектов, позволяет определить значения Λ для каждого из них. Сравнение этих теоретических предсказаний, полученных на основе различных моделей гравитации и уравнений состояния, с наблюдаемыми данными позволяет проверить эти модели и ограничить их параметры, что является ключевым для понимания природы гравитации и свойств плотной материи.
Байесовский вывод предоставляет статистическую основу для определения параметров моделей модифицированной гравитации f(Q) на основе наблюдательных данных. Этот метод позволяет оценить вероятностное распределение параметров модели, учитывая априорные знания и правдоподобие данных, полученных из наблюдений нейтронных звезд, таких как массы и радиусы, а также деформации приливных сил, измеряемые с помощью гравитационных волн. В рамках байесовского подхода формируется функция правдоподобия, отражающая соответствие теоретических предсказаний модели f(Q) наблюдаемым данным. Затем, используя теорему Байеса, рассчитывается апостериорное распределение параметров, которое отражает обновленные знания о параметрах модели после учета наблюдательных данных. Этот процесс позволяет количественно оценить неопределенности в параметрах модели и сравнить различные модели f(Q) на основе их способности объяснять наблюдаемые свойства нейтронных звезд.
Ограничение f(Q) Гравитации с Наблюдениями NICER
Наблюдения, проводимые при помощи прибора NICER, предоставляют бесценные данные о массах и радиусах нейтронных звезд, что открывает уникальную возможность для проверки различных теорий гравитации. Нейтронные звезды, являясь самыми плотными объектами во Вселенной, испытывают экстремальные гравитационные эффекты, которые позволяют выявить отклонения от предсказаний общей теории относительности Эйнштейна. Точное измерение их параметров, таких как масса и радиус, является критически важным для тестирования альтернативных моделей гравитации, включая теории, модифицирующие закон всемирного тяготения. Именно эти высокоточные данные, полученные NICER, позволяют ученым строить более строгие ограничения на параметры этих теорий и оценивать, насколько хорошо они согласуются с наблюдаемой реальностью, что, в конечном итоге, приближает нас к пониманию фундаментальной природы гравитации.
Сравнение предсказаний различных моделей теории f(Q) гравитации с данными, полученными при помощи прибора NICER, позволяет количественно оценить, насколько эти модели согласуются с наблюдаемой реальностью. В рамках этого подхода, наблюдаемые массы и радиусы нейтронных звезд служат ключевыми параметрами для проверки отклонений от общей теории относительности Эйнштейна. Анализ данных NICER предоставляет возможность установить ограничения на параметры моделей f(Q), тем самым сужая область допустимых модификаций гравитации. В частности, различия в предсказаниях различных функциональных форм для f(Q) — экспоненциальной, логарифмической и линейной — проявляются в предсказываемых максимальных массах нейтронных звезд и их деформируемости под воздействием приливных сил, что делает возможным статистическое оценивание вероятности каждой модели на основе наблюдаемых данных.
Байесовский анализ, проведенный на основе данных, полученных с помощью NICER, указывает на то, что модель экспоненциальной функции f(Q) обладает наибольшей статистической поддержкой среди исследуемых вариантов модифицированной гравитации. Значение фактора Байеса, равное ln(BF) = -0.35 по отношению к логарифмической модели и ln(BF) = -1.28 по отношению к линейной модели, свидетельствует о том, что экспоненциальная функция лучше всего согласуется с наблюдаемыми характеристиками нейтронных звезд. Такое превосходство в статистической поддержке позволяет предположить, что данная модель может быть более точным описанием гравитационных взаимодействий в экстремальных условиях, существующих внутри этих плотных объектов, и, следовательно, предоставляет важные данные для дальнейшего изучения модификаций общей теории относительности.
Результаты анализа показали, что различные модели модифицированной гравитации f(Q) предсказывают различные характеристики нейтронных звезд. В частности, логарифмическая модель предсказывает максимальную массу нейтронной звезды, равную 2.36 M_{\odot}, что является важным ограничением для ее физической состоятельности. Экспоненциальная модель, в свою очередь, дает значение деформабельности приливных сил \Lambda_{1.4} = 156.95. Данные значения позволяют сопоставить теоретические предсказания с наблюдаемыми данными, полученными, например, с помощью NICER, и оценить, насколько хорошо каждая модель соответствует реальным нейтронным звездам, что, в конечном итоге, способствует более глубокому пониманию фундаментальной природы гравитации.
Исследование, представленное в данной работе, демонстрирует изящество подхода к пониманию фундаментальных свойств нейтронных звёзд в рамках модифицированной гравитации f(Q). Авторы, используя байесовский вывод и данные наблюдений NICER, стремятся к гармонии между теорией и экспериментом. Этот поиск оптимальной функциональной формы f(Q) напоминает о стремлении к элегантности в научном познании. Как однажды заметил Исаак Ньютон: «Я не знаю, как я выгляжу в глазах других, но, когда я смотрю на звезды, я чувствую себя счастливым». Подобно тому, как астрономические наблюдения вдохновляли Ньютона, так и данные NICER позволяют исследователям пролить свет на загадки гравитации и структуры нейтронных звёзд, подтверждая, что экспоненциальная модель является наиболее статистически обоснованной.
Куда же дальше?
Представленная работа, подобно тщательно настроенному инструменту, позволила оценить параметры нейтронных звезд в рамках теории $f(Q)$ гравитации. Однако, гармония этой оценки не должна вводить в заблуждение. Наиболее вероятная экспоненциальная форма $f(Q)$, хотя и предпочтительна статистически, не является окончательным аккордом. Остается вопрос о физической природе этой функции, о её связи с более фундаментальными принципами, которые пока ускользают от понимания. Интерфейс модели «поёт», но слышен ли в этой мелодии голос истинной физики?
Следующим шагом представляется не только усложнение модели, но и поиск альтернативных функциональных форм $f(Q)$, возможно, вдохновленных другими модификациями гравитации или даже квантовой гравитацией. Необходимо учитывать систематические ошибки, связанные с упрощениями в моделировании нейтронных звезд и анализе данных NICER. Каждая деталь важна, даже та, которую не замечают сразу, — незначительное отклонение может раскрыть новые горизонты.
В конечном счете, задача состоит не в том, чтобы просто «подогнать» модель к данным, а в том, чтобы создать стройную и элегантную теорию, способную объяснить не только свойства нейтронных звезд, но и другие космологические явления. Элегантность — не опция; это признак глубокого понимания. И только тогда эта мелодия зазвучит во всей своей полноте.
Оригинал статьи: https://arxiv.org/pdf/2601.16227.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Все рецепты культистского круга в Escape from Tarkov
- Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip
- Решение головоломки с паролем Absolum в Yeldrim.
- Лучшие транспортные средства в Far Cry 6
- Лучшие шаблоны дивизий в Hearts Of Iron 4
- Необходимо: Как выращивать урожай
- Где найти и поймать бабочку Солнечного луча в Палии
- All Valley Pass Aurylene Locations In Endfield
- Dragon’s Dogma 2: Где найти Драконорожденных
- Как получить скины Alloyed Collective в Risk of Rain 2
2026-01-26 19:50