Неприступная точка: энтропийный барьер на конической пересекающей поверхности

Автор: Денис Аветисян

Новое исследование показывает, что классические молекулярные динамические расчеты сталкиваются с непреодолимым препятствием при попытке достичь конической пересекающей поверхности, ограничивая точность моделирования неадиабатических процессов.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал

В исследовании охарактеризована коническая пересекаемость между основным и первым возбужденным синглетными состояниями катиона метаниминия (<span class="katex-eq" data-katex-display="false">CH_2NH_2^{+}</span>), демонстрирующая характерную двойконическую топографию потенциальных энергетических поверхностей вблизи точки вырождения <span class="katex-eq" data-katex-display="false">S_1/S_0</span> вдоль координат, определяющих плоскость ветвления. — В исследовании охарактеризована коническая пересекаемость между основным и первым возбужденным синглетными состояниями катиона метаниминия ( $CH_2NH_2^{+}$ ), демонстрирующая характерную двойконическую топографию потенциальных энергетических поверхностей вблизи точки вырождения $S_1/S_0$ вдоль координат, определяющих плоскость ветвления.

Классические траектории не могут достичь конической пересекающей поверхности из-за возникающего энтропийного барьера, ограничивающего возможности смешанных квантово-классических методов.

Несмотря на широкое использование конических пересечений в объяснении неадиабатических процессов, моделирование точного достижения этих точек в молекулярной динамике остается сложной задачей. В работе, озаглавленной ‘The Entropic Barrier around the Conical Intersection Seam’, авторы исследуют причины этого явления, используя модель вибронного взаимодействия и молекулярные динамические симуляции. Показано, что по мере приближения к коническому пересечению возникает бесконечный барьер свободной энергии, препятствующий достижению точки вырождения. Может ли это объяснять успешность смешанных квантово-классических методов в описании неадиабатических процессов без необходимости точного моделирования вырожденных состояний?

За гранью приближения Борна-Оппенгеймера: Пророчество сбоя

Традиционные методы молекулярной динамики опираются на приближение Борна-Оппенгеймера, которое предполагает разделение движения электронов и ядер. Данное упрощение основывается на значительном различии в массах этих частиц, позволяя рассматривать электронную структуру как мгновенно адаптирующуюся к изменениям в ядерных координатах. Это позволяет значительно снизить вычислительную сложность моделирования молекулярных процессов, рассматривая потенциальную энергию как функцию только от ядерных координат. Однако, такое разделение является лишь приближением, и его точность ограничена, особенно в ситуациях, когда электронные состояния сближаются по энергии, что приводит к нарушению данного приближения и необходимости использования более сложных методов, учитывающих взаимосвязь между электронными и ядерными степенями свободы.

Приближение Борна-Оппенгеймера, являющееся основой большинства молекулярно-динамических симуляций, оказывается несостоятельным в точках, известных как конические пересечения. В этих точках энергетические поверхности различных электронных состояний сближаются, и разделение между ядерным и электронным движением теряет смысл. Это существенно затрудняет точное моделирование неадиабатических процессов — переходов между электронными состояниями, происходящих без поглощения или излучения света. Именно такие процессы лежат в основе многих фотохимических реакций, например, фотосинтеза или фоторазложения молекул, и их адекватное описание требует методов, учитывающих явное взаимодействие между электронными состояниями и ядерным движением, что представляет собой серьезную вычислительную задачу.

Для адекватного моделирования неадиабатических процессов, лежащих в основе фотохимии и других явлений, необходимы методы, явно учитывающие связь между электронными состояниями и движением ядер. Традиционные подходы, основанные на приближении Борна-Оппенгеймера, оказываются недостаточными вблизи конических пересечений, где данная связь становится критически важной. Современные вычислительные стратегии, такие как поверхностные ходы и методы смешанных квантово-классических расчетов, направлены на преодоление этого ограничения, позволяя отслеживать динамику системы при переходах между электронными состояниями. Эти методы, хотя и требуют значительных вычислительных ресурсов, открывают возможности для детального изучения процессов, определяющих химические реакции и энергетический ландшафт молекул, что крайне важно для разработки новых материалов и технологий.

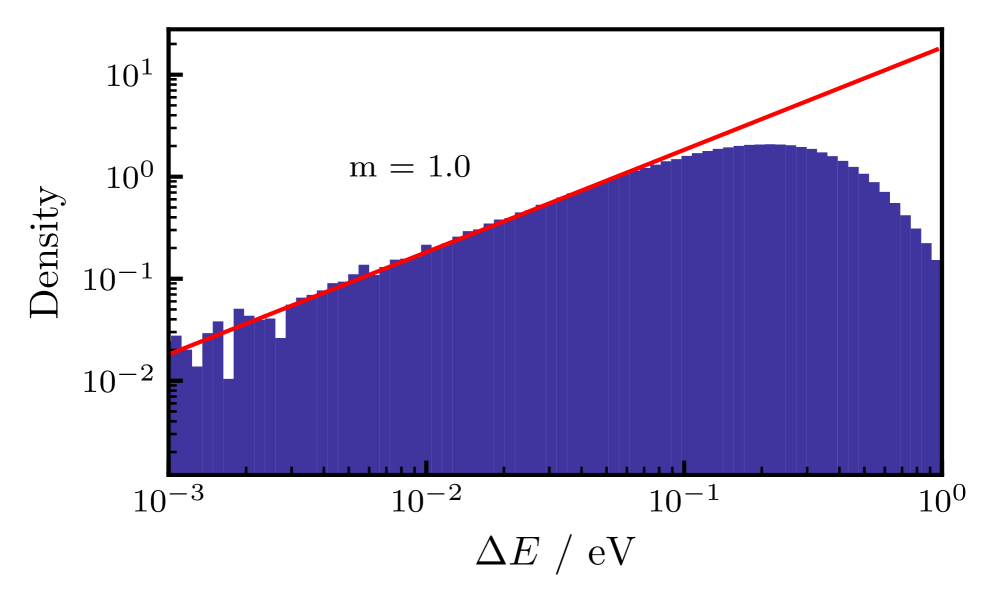
Гистограмма адиабатического энергетического зазора между основным и первым возбужденным синглетным состояниями для <span class="katex-eq" data-katex-display="false"> ext{CH}_2 ext{NH}_2^+</span> демонстрирует степенной закон в области малых значений зазора, показатель степени которого определяет зависимость плотности состояний от величины этого зазора. — Гистограмма адиабатического энергетического зазора между основным и первым возбужденным синглетным состояниями для $ext{CH}_2 ext{NH}_2^+$ демонстрирует степенной закон в области малых значений зазора, показатель степени которого определяет зависимость плотности состояний от величины этого зазора.

Смешанный подход к моделированию неадиабатической динамики

Смешанные квантово-классические (MQC) симуляции представляют собой подход к моделированию неадиабатической динамики, основанный на принципиальном разделении описания электронных и ядерных степеней свободы. В рамках MQC электроны рассматриваются квантовомеханически, что позволяет учесть их волновые свойства и туннелирование, в то время как ядра описываются классически, как частицы, движущиеся по классическим траекториям. Такой подход позволяет снизить вычислительную сложность по сравнению с полностью квантовомеханическими расчетами, сохраняя при этом адекватное описание процессов, происходящих при пересечении потенциальных энергетических поверхностей, что особенно важно для изучения фотохимии и других неадиабатических явлений.

Метод траекторного перескока между поверхностями потенциальной энергии (Trajectory Surface Hopping, TSH) представляет собой мощный подход в рамках смешанных квантово-классических (MQC) вычислений. Он позволяет моделировать динамику систем, где происходит переход между различными электронными состояниями, представленными разными поверхностями потенциальной энергии. В процессе симуляции, классические траектории ядер могут «перескакивать» с одной поверхности на другую с определенной вероятностью, определяемой неадиабатическими условиями. Вероятность перехода рассчитывается на основе скалярного произведения градиентов волновых функций на разных поверхностях, что обеспечивает учет электрон-ядерного взаимодействия и позволяет описывать процессы, происходящие вблизи конических пересечений, такие как фотохимические реакции и внутримолекулярные переходы энергии.

Методы смешанной квантово-классической динамики, реализованные в программных пакетах, таких как SHARC 4.0, позволяют проводить исследования процессов, протекающих на конических пересечениях. Эти пересечения представляют собой области на потенциальной энергии поверхности, где две или более электронные поверхности сближаются, что приводит к эффективному переносу электронной плотности и, как следствие, к неадиабатическим переходам. Использование SHARC 4.0 и подобных инструментов позволяет моделировать динамику молекул вблизи этих точек, определяя вероятности межсистемных переходов, времена релаксации и другие важные характеристики, необходимые для понимания фотохимии, фотофизики и других процессов, происходящих в сложных молекулярных системах.

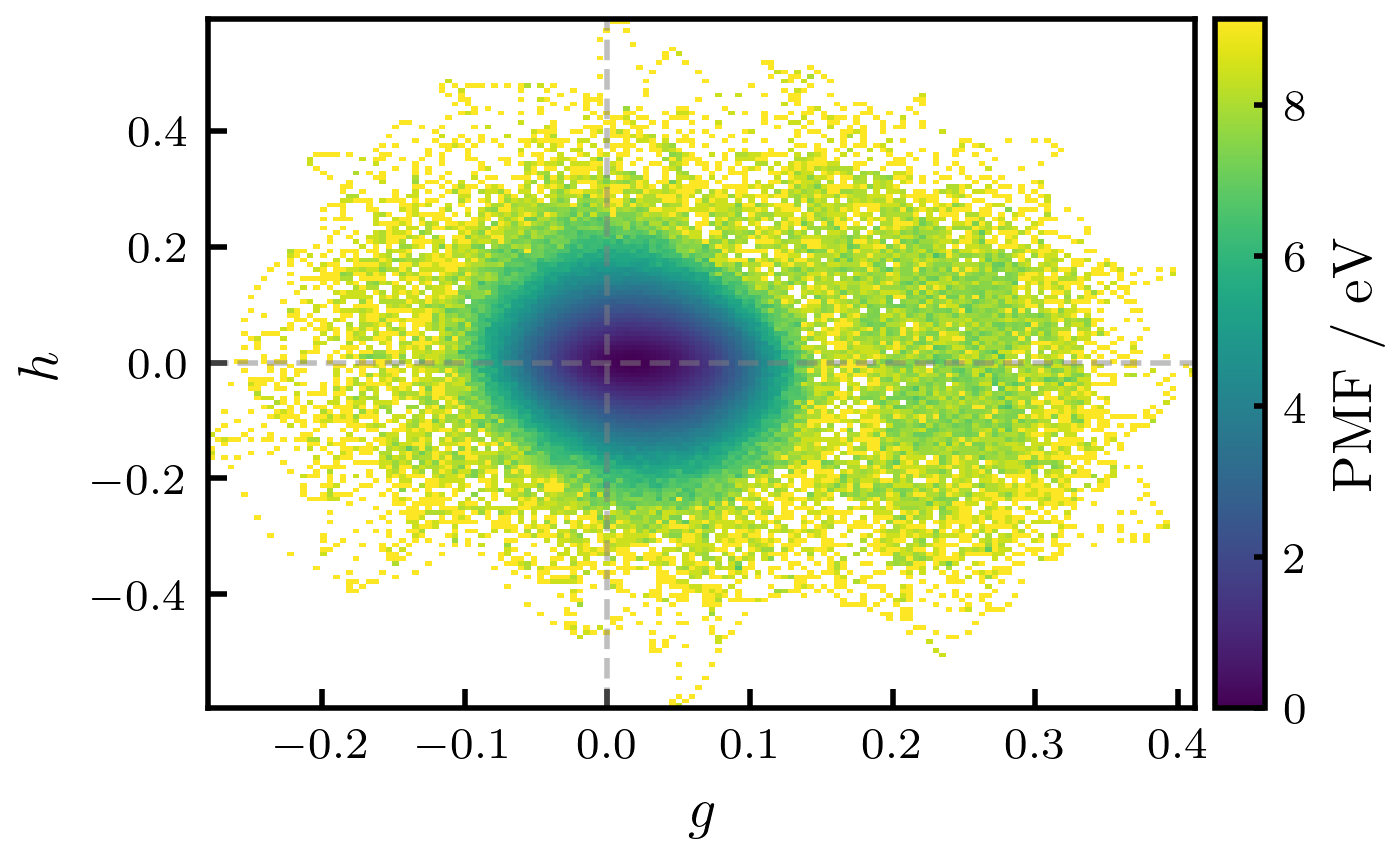
Двумерная поверхность свободной энергии как функция координат, характеризующих разницу градиентов и неадиабатическое взаимодействие, показывает точку минимальной энергии, соответствующую геометрии MECI при <span class="katex-eq" data-katex-display="false">g=0</span> и <span class="katex-eq" data-katex-display="false">h=0</span>. — Двумерная поверхность свободной энергии как функция координат, характеризующих разницу градиентов и неадиабатическое взаимодействие, показывает точку минимальной энергии, соответствующую геометрии MECI при $g=0$ и $h=0$ .

Понимание ландшафта потенциальной энергии: Признаки будущего сбоя

В молекуле метиминиевого катиона, пересечение потенциальных поверхностей состояний S1 и S0 представляет собой значительную проблему из-за наличия энтропийного барьера. Этот барьер обусловлен квантовомеханическими эффектами, в частности, колебаниями нулевой точки и эффектом туннелирования, которые препятствуют достижению точки минимальной энергии на коническом пересечении. В результате, неадиабатические переходы замедляются, поскольку классические траектории движения молекул статистически запрещены для достижения области конического пересечения. Высота энтропийного барьера определяется анализом свободной энергии с использованием коллективных переменных, таких как энергетический зазор.

Наличие энтропийного барьера, обусловленного колебаниями нулевой точки и квантовым туннелированием, существенно затрудняет достижение минимальной точки конического пересечения в катионе метиминия. Данный барьер приводит к снижению вероятности неадиабатических переходов, поскольку классические траектории молекулярной динамики статистически запрещены для достижения области конического пересечения. Эффект усиливается из-за того, что энергия, необходимая для преодоления барьера, связана не только с потенциальной энергией, но и с энтропийным вкладом, вызванным квантовыми колебаниями молекулы.

Анализ свободной энергии, использующий коллективные переменные, такие как энергетическая щель, имеет решающее значение для понимания высоты и влияния энтропийного барьера в метан иминиевом катионе. Исследование показало, что классические траектории молекулярной динамики статистически запрещены для достижения шва конического пересечения из-за наличия этого барьера, причём свободная энергия стремится к бесконечности при приближении энергетической щели к нулю. Данный результат указывает на то, что для преодоления барьера требуется значительная активационная энергия, недоступная в классической механике, и подчеркивает важность квантово-механических эффектов в описании динамики этого процесса.

Анализ свободной энергии показал, что высота энергетического барьера на коническом пересечении (CI) стремится к бесконечности непосредственно на CI-шве. Это означает, что классические траектории молекулярной динамики статистически не могут достичь данного шва. При этом, размерность CI-шва, определяемая как количество независимых координат, необходимых для описания движения вдоль шва, составляет 3N-8, где N — общее число степеней свободы молекулы. Данная размерность обусловлена сохранением углового момента и ограничениями, накладываемыми геометрией молекулы вблизи конического пересечения.

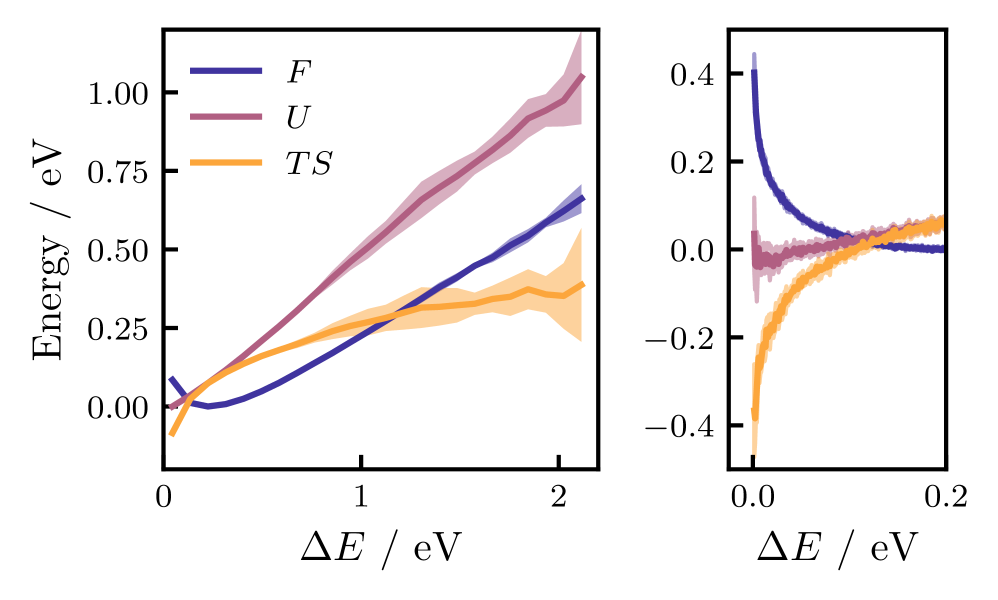
Анализ динамики <span class="katex-eq" data-katex-display="false">CH_2NH_2^{+}_{2}</span> показал, что свободная энергия, внутренняя энергия и энтропия изменяются в зависимости от энергетической щели <span class="katex-eq" data-katex-display="false">ΔE</span>, при этом заштрихованные области указывают на стандартное отклонение между траекториями, а минимальные значения свободной энергии и внутренней энергии смещены к нулю для наглядности, все энергии указаны в электрон-вольтах. — Анализ динамики $CH_2NH_2^{+}_{2}$ показал, что свободная энергия, внутренняя энергия и энтропия изменяются в зависимости от энергетической щели $ΔE$ , при этом заштрихованные области указывают на стандартное отклонение между траекториями, а минимальные значения свободной энергии и внутренней энергии смещены к нулю для наглядности, все энергии указаны в электрон-вольтах.

Последствия для управления фотохимическими реакциями: Семена будущего

Точное моделирование неадиабатической динамики в точках конического пересечения имеет решающее значение для понимания и управления фотохимическими реакциями. Эти точки, где энергетические поверхности различных электронных состояний пересекаются, являются ключевыми участками, определяющими исход реакции. Без адекватного описания динамики вблизи этих пересечений, предсказать, какой продукт будет образован и с какой скоростью, становится невозможно. Современные вычислительные методы, такие как поверхностные скачки и траекторные методы, позволяют исследовать эту динамику, но требуют высокой точности в описании потенциальных энергетических поверхностей и электронно-вибрационного взаимодействия. Развитие этих методов и их применение к различным фотохимическим процессам открывает возможности для целенаправленного управления реакциями, например, для повышения эффективности фотосинтеза или разработки новых фотокатализаторов.

Линейная модель вибронного взаимодействия представляет собой ключевой инструмент для описания связи между электронными и колебательными состояниями вблизи конических пересечений. Данная модель предполагает, что взаимодействие между электронными состояниями происходит линейно относительно нормальным координатам колебаний, что позволяет упростить анализ и расчеты динамики реакций. В рамках этой модели, коническая точка пересечения рассматривается как место, где энергетические поверхности различных электронных состояний приближаются, обеспечивая возможность нерадиационного перехода между ними. Математически, взаимодействие описывается через параметры вибронной связи, определяющие силу влияния колебаний на электронную структуру. Использование этой модели позволяет не только понять механизм протекания фотохимических реакций, но и предсказать их эффективность и селективность, что критически важно для разработки новых материалов и технологий.

Исследования показывают, что целенаправленное изменение потенциальной энергии реакционной системы, а также преодоление присущего ей энтропийного барьера, открывает перспективы для повышения эффективности управления фотохимическими реакциями. Вместо случайного распределения энергии между различными реакционными путями, возможно направленное стимулирование конкретных процессов, что позволяет увеличивать выход целевых продуктов и минимизировать образование нежелательных побочных соединений. Такой подход предполагает тонкую настройку энергетических уровней и использование внешних воздействий для создания благоприятных условий для протекания желаемой реакции, представляя собой перспективную стратегию в разработке новых фотохимических технологий и материалов.

Исследование демонстрирует, что классические методы молекулярной динамики сталкиваются с непреодолимым барьером при приближении к коническому пересечению. Траектории, стремясь к точке вырождения, будто бы упираются в невидимую стену энтропии. Это напоминает о неизбежности хаоса, о том, что порядок — лишь временный кэш между сбоями. Как точно подметил Альберт Эйнштейн: «Самое прекрасное, что мы можем испытать, — это тайна». Ведь и в этой работе тайна заключается не в невозможности достижения конического пересечения, а в понимании природы этого энтропийного барьера, который проявляется как фундаментальное ограничение классических траекторий.

Что дальше?

Представленная работа демонстрирует не просто техническую сложность достижения конического пересечения посредством классического моделирования, но и фундаментальное ограничение самого подхода. Траектории, стремящиеся к точке вырождения, наталкиваются на энтропийный барьер, подобно путникам, ищущим абсолютный ноль температуры. Разделение системы на классическую и квантовую части не снимает проблемы, а лишь откладывает неизбежное — столкновение с принципиальной невозможностью полного описания динамики. Всё, что разделено, рано или поздно сойдётся к одному состоянию.

Будущие исследования, вероятно, будут сосредоточены на разработке более изощрённых смешанных квантово-классических методов, но стоит задуматься, не является ли сама идея точного моделирования неадиабатических процессов утопией. Усилия, направленные на обход энтропийного барьера, могут лишь усугубить проблему, порождая новые артефакты и зависимости. Зачем стремиться к детальному описанию траекторий, если сама поверхность потенциальной энергии неизбежно искажается шумом и приближениями?

Представляется, что более плодотворным направлением является разработка концептуальных моделей, способных описывать общую картину неадиабатических процессов, не требуя точного знания траекторий. Попытки «вырастить» систему, а не «построить» её, могут привести к более устойчивым и полезным результатам. В конечном итоге, всё стремится к зависимости, и попытки избежать этого — лишь иллюзия.

Оригинал статьи: https://arxiv.org/pdf/2602.02115.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-03 17:57