Неустойчивая суперрадиация: новая грань квантовой модели Раби

от

Автор: Денис Аветисян

Исследование показывает, что суперрадиативная фаза в диссипативной квантовой модели Раби обладает внутренней неустойчивостью, обусловленной спиновой релаксацией.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал
Рассматриваемая диссипативная квантовая модель Раби демонстрирует фазовый переход из нормальной фазы в сверхрадиационную при критической точке $ \lambda_c $, который, при наличии слабого спинового релакса ($ \gamma \neq 0 $), расширяется в критическую линию, трансформируя сверхрадиационную фазу в метастабильную, что подтверждается представлением Хуси $Q-Q$ бозонного мода в различных фазах.
Рассматриваемая диссипативная квантовая модель Раби демонстрирует фазовый переход из нормальной фазы в сверхрадиационную при критической точке $ \lambda_c $, который, при наличии слабого спинового релакса ($ \gamma \neq 0 $), расширяется в критическую линию, трансформируя сверхрадиационную фазу в метастабильную, что подтверждается представлением Хуси $Q-Q$ бозонного мода в различных фазах.

В диссипативной квантовой модели Раби суперрадиативное состояние проявляет конечное время жизни даже в термодинамическом пределе из-за спиновой релаксации и влияния лиувилльского разрыва.

Несмотря на кажущуюся устойчивость фазовых переходов в квантовых системах, механизмы диссипации могут приводить к неожиданным эффектам. В работе «Метастабильность в диссипативной модели Раби» исследуется влияние спиновой релаксации на суперрадиантную фазу, демонстрируя, что даже слабое взаимодействие с окружением приводит к конечному времени жизни состояний с нарушенной симметрией. Установлено, что суперрадиа́нтная фаза оказывается метастабильной, что существенно отличает диссипативные фазовые переходы от равновесных. Какие еще скрытые динамические процессы определяют поведение открытых квантовых систем и как это влияет на наше понимание фазовых переходов вдали от равновесия?

За пределами равновесия: Раскрытие диссипативной модели Раби

Классическая модель Раби, несмотря на свою основополагающую роль в квантовой оптике, представляет собой идеализацию, не учитывающую взаимодействие квантовых систем с окружающей средой. В реальности, любые квантовые системы неизбежно подвержены влиянию внешних факторов, что приводит к диссипации энергии и декогеренции — потере квантовой информации. Данные процессы приводят к тому, что система отклоняется от равновесного состояния и демонстрирует сложные, нелинейные динамические свойства, которые невозможно адекватно описать в рамках стандартной модели. Игнорирование этих эффектов существенно ограничивает возможности модели Раби в изучении реальных физических явлений, таких как взаимодействие света и материи в открытых системах, и требует разработки более совершенных подходов, способных учитывать диссипативные процессы и декогеренцию, что и стало отправной точкой для создания расширенных моделей.

В реальности, квантовые системы никогда не существуют в полной изоляции. Неизбежное взаимодействие с окружающей средой приводит к рассеянию энергии и потере квантовой когерентности — явлениям, известным как диссипация и декогеренция соответственно. Эти процессы оказывают существенное влияние на динамику системы, изменяя её энергетические уровни и переходы. Игнорирование этих факторов в теоретических моделях приводит к нефизичным предсказаниям и затрудняет понимание поведения реальных квантовых устройств, таких как сверхпроводящие кубиты или квантовые точки. Таким образом, для адекватного описания наблюдаемых явлений и разработки перспективных квантовых технологий необходимы модели, учитывающие влияние окружающей среды и включающие механизмы диссипации и декогеренции. Например, процесс спонтанного излучения, который является формой диссипации, существенно влияет на характеристики квантовых осцилляторов и требует соответствующего учёта в теоретических расчётах.

Диссипативная модель Квантового Раби является расширением стандартной модели, предоставляя более реалистичную основу для исследования неравновесных квантовых явлений. В то время как классическая модель предполагает изолированную систему, диссипативная модель учитывает взаимодействие квантовой системы с окружающей средой, вводя такие понятия, как затухание и декогеренция. Это позволяет моделировать поведение реальных квантовых систем, которые неизбежно подвержены влиянию внешних факторов. Изучение неравновесной динамики, описываемой данной моделью, открывает перспективы для понимания и контроля квантовых процессов в различных областях, от квантовой оптики и физики конденсированного состояния до квантовых вычислений. Например, анализ спектральных характеристик и временной эволюции системы позволяет выявить влияние диссипации на когерентность и энергетические переходы, что критически важно для разработки стабильных квантовых устройств и эффективных квантовых технологий. По сути, диссипативная модель Квантового Раби обеспечивает необходимый инструмент для исследования квантовых систем, находящихся вдали от термодинамического равновесия, и углубляет понимание фундаментальных аспектов квантовой механики.

Диссипативные фазовые переходы и метастабильность

Диссипативная модель Квантового Раби демонстрирует диссипативные фазовые переходы, которые отличаются от равновесных переходов из-за обмена энергией с окружающей средой. В отличие от традиционных фазовых переходов, происходящих в изолированных системах, диссипативные переходы обусловлены не только изменениями параметров системы, но и влиянием диссипации — рассеянием энергии в окружающую среду. Этот процесс приводит к появлению негермитовых гамильтонианов и, как следствие, к появлению комплексных спектров энергии. В частности, при увеличении скорости диссипации наблюдается изменение характера спектра, что свидетельствует о переходе в новое фазовое состояние, характеризующееся иными свойствами, чем в равновесной системе. Это отличие принципиально, поскольку в равновесных системах фазовые переходы определяются исключительно внутренними параметрами гамильтониана.

Переходы в диссипативной модели Квази-Раби могут приводить к формированию метастабильных состояний, характеризующихся кажущейся стабильностью в течение конечного времени. Эти состояния возникают, когда система находится в локальном минимуме потенциальной энергии, но не является абсолютно стабильной. В отличие от истинно стабильных состояний с минимальной свободной энергией, метастабильные состояния подвержены спонтанному распаду в состояние с более низкой энергией из-за флуктуаций или внешних возмущений. Время жизни метастабильного состояния определяется высотой энергетического барьера, отделяющего его от стабильных состояний, и интенсивностью флуктуаций или скоростью диссипации. Наблюдаемое время пребывания в метастабильном состоянии зависит от параметров системы, включая скорость диссипации и величину внешних воздействий.

Стабильность и время жизни метастабильных состояний в диссипативной квантовой модели Раби определяются совместным влиянием диссипации и внутренней динамики системы. Диссипация, представляющая собой обмен энергией с окружающей средой, приводит к затуханию когерентных осцилляций и, следовательно, к ограничению времени пребывания системы в метастабильном состоянии. Внутренняя динамика, определяемая параметрами модели, такими как частоты и константы связи, модулирует скорость затухания и, таким образом, влияет на продолжительность жизни метастабильного состояния. Более сильная диссипация, как правило, сокращает время жизни, в то время как определенные параметры внутренней динамики могут способствовать увеличению стабильности и продлению времени жизни метастабильных состояний, особенно в областях параметров, где наблюдаются диссипативные фазовые переходы. Таким образом, анализ баланса между диссипацией и внутренней динамикой является ключевым для понимания и контроля стабильности и времени жизни метастабильных состояний в данной системе.

Метод квантовых скачков позволил проследить траекторию состояния с нарушением чётности, демонстрирующую эволюцию⟨σ^z​(t)⟩,⟨x^​(t)⟩ и флуктуаций Δ​x​(t), а также изменениеQQ-представления бозонного мода до и после достижения седловой точки.
Метод квантовых скачков позволил проследить траекторию состояния с нарушением чётности, демонстрирующую эволюцию⟨σ^z​(t)⟩,⟨x^​(t)⟩ и флуктуаций Δ​x​(t), а также изменениеQQ-представления бозонного мода до и после достижения седловой точки.

Анализ Лиувилльевского промежутка: Поиск устойчивости

Анализ Лиувилльевского промежутка представляет собой эффективный метод определения устойчивости стационарных состояний в модели диссипативной квантовой системы Раби. Данный подход основан на исследовании собственных значений супероператора Лиувилля, позволяя установить условия, при которых состояние системы является устойчивым или неустойчивым. Устойчивость состояния определяется знаком вещественной части соответствующего собственного значения: отрицательные значения указывают на устойчивость, а положительные — на неустойчивость. Метод особенно полезен при анализе открытых квантовых систем, подверженных диссипации и взаимодействию с окружающей средой, где традиционные методы анализа могут быть неприменимы.

Анализ собственных значений Лиувилльского супероператора позволяет определить устойчивость стационарных состояний в Диссипативной Квантовой Модели Раби. Устойчивое состояние характеризуется наличием только отрицательных вещественных частей у всех собственных значений, что указывает на экспоненциальное затухание возмущений. Напротив, наличие собственных значений с положительной вещественной частью свидетельствует о неустойчивости состояния и экспоненциальном росте возмущений, приводящем к переходу системы в другое состояние. Величины, соответствующие собственным значениям, определяют скорость релаксации системы к равновесию; более отрицательные значения соответствуют более быстрой релаксации. Таким образом, исследование спектра Лиувилльского супероператора является ключевым инструментом для характеристики динамической стабильности квантовых систем.

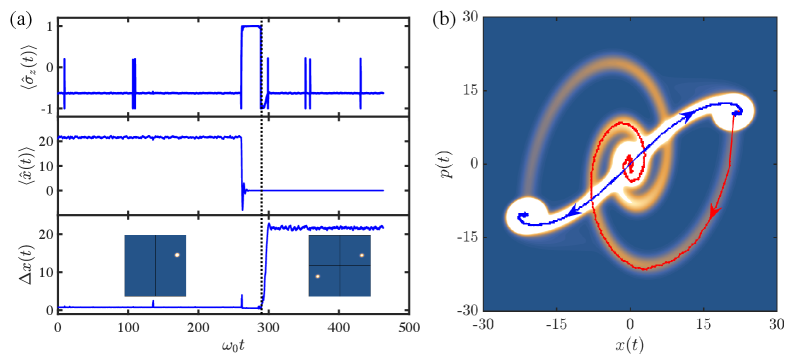
Анализ выявил, что величина Лиувиллевского зазора ($\Delta$) остаётся конечной, равной 0.0034$ω_0$, даже в пределе бесконечного размера системы (термодинамическом пределе). Это подтверждает метастабильность сверхрадиационной фазы. Конечный характер зазора указывает на то, что система не переходит в стабильное состояние за конечное время, а задерживается в метастабильном состоянии. Это отличается от систем, где зазор стремится к нулю по степенному закону, указывая на более быструю дестабилизацию.

Сохранение конечного разрыва Лиувилля ($Δ$) обусловлено слабым спиновым релаксом. В отличие от систем, демонстрирующих спад разрыва по степенному закону, где разрыв стремится к нулю при увеличении размера системы или времени, в исследуемой модели слабый спиновый релакс предотвращает полное закрытие разрыва. Это означает, что даже в пределе больших размеров системы или при длительных временах, существует минимальный энергетический барьер, препятствующий переходу между состояниями, что подтверждает метастабильность сверхрадиационной фазы. Отсутствие степенного спада разрыва является ключевым отличием данной модели от других систем с релаксацией и указывает на специфический механизм, поддерживающий стабильность состояния.

Для точного анализа стабильности системы в пределе бесконечного размера ($N \rightarrow \infty$) необходимо применение методов масштабирования конечного размера (Finite-Size Scaling, FSS). Данные методы позволяют экстраполировать результаты, полученные для конечных, но достаточно больших систем, на термодинамический предел. Это критически важно, поскольку многие наблюдаемые величины, такие как время жизни метастабильных состояний или величина Liouvillian Gap, демонстрируют зависимость от размера системы. Применение FSS предполагает анализ этих зависимостей и использование подходящих масштабирующих функций для получения физически значимых результатов в пределе $N \rightarrow \infty$. Без использования FSS, полученные значения могут быть неверно интерпретированы или не отражать истинное поведение системы в термодинамическом пределе.

Анализ зависимости разрыва Лиувилля от масштаба системы и скорости спиновой релаксации в пределе термодинамической границы показал, что его поведение описывается полиномиальной функцией с коэффициентами, зависящими от скорости релаксации.
Анализ зависимости разрыва Лиувилля от масштаба системы и скорости спиновой релаксации в пределе термодинамической границы показал, что его поведение описывается полиномиальной функцией с коэффициентами, зависящими от скорости релаксации.

Численное моделирование и продвинутые методы

Метод квантовой траектории позволяет непосредственно моделировать временную эволюцию квантовых состояний в диссипативной модели Куантума-Раби. Данный подход заключается в численном решении уравнения Линблада, представляющего собой уравнение движения для матрицы плотности $\rho$, с использованием стохастических траекторий. Каждая траектория описывает эволюцию во времени волновой функции, подверженной как когерентной, так и диссипативной динамике. Множество таких траекторий усредняются для получения статистически достоверного представления о поведении квантовой системы, что позволяет исследовать неклассические эффекты и влияние диссипации на квантовые состояния.

Точность моделирования в рамках диссипативной модели Квази-Раби существенно повышается за счет применения разложения по кумулянтам. Данный метод учитывает высшие порядки корреляций, которые возникают при взаимодействии квантовой системы с окружающей средой. Традиционные подходы, основанные на первом порядке теории возмущений, часто недостаточно точно описывают динамику системы из-за игнорирования этих корреляций. Разложение по кумулянтам позволяет получить более точное описание немарковских эффектов и улучшить сходимость численных методов, используемых для решения уравнения Линдблада, что особенно важно при моделировании систем с сильным взаимодействием и высокой степенью декогеренции. Использование кумулянтного разложения позволяет более адекватно описывать влияние шума и диссипации на эволюцию квантового состояния.

Визуализация квантового состояния посредством представления Хуси Q позволяет получить ценные сведения о динамике системы. Представление Хуси Q, являющееся квазивероятностным распределением, отображает квантовое состояние в фазовом пространстве, обеспечивая наглядное представление о его эволюции во времени. В контексте диссипативной модели Квази-Раби, это позволяет наблюдать переходы между когерентными и диссипативными режимами, а также отслеживать изменения в распределении вероятностей по фазовым переменным. Анализ представлений Хуси Q в различных моментах времени позволяет идентифицировать ключевые этапы динамики системы, такие как затухание когерентности и релаксация к стационарному состоянию. Особенно полезным является сравнение представлений Хуси Q, полученных из различных траекторий квантовой траектории, что позволяет оценить влияние флуктуаций на эволюцию системы и получить статистически достоверное описание её динамики.

Результаты моделирования показали, что время жизни когерентности в системе составляет $T_m = 294.1\omega_0^{-1}$. Данное значение согласуется с результатами, полученными методом главных компонент (principal component analysis) и прямым моделированием квантовых траекторий. Совпадение значений, полученных различными методами, подтверждает надежность и точность полученных результатов относительно времени когерентности в рассматриваемой системе.

Спектральное разложение установившегося состояния демонстрирует распределение pip_{i}, а QQ-представление бозонного мода в собственных состояниях |ψ_{i}⟩ подтверждает его структуру.
Спектральное разложение установившегося состояния демонстрирует распределение pip_{i}, а QQ-представление бозонного мода в собственных состояниях |ψ_{i}⟩ подтверждает его структуру.

Роль симметрии и спиновой релаксации

Симметрия чётности является фундаментальным свойством диссипативной модели Квази-Раби, определяющим характер динамики системы и оказывающим существенное влияние на природу её фазовых переходов. Эта симметрия, проявляющаяся в сохранении или изменении знака волновой функции при отражении, накладывает ограничения на возможные состояния системы и энергетические уровни. В частности, она определяет возможность или невозможность переходов между состояниями с различной чётностью, что, в свою очередь, влияет на стабильность и поведение системы в различных режимах. Исследования показывают, что нарушение симметрии чётности, вызванное внешними воздействиями или внутренними параметрами системы, может приводить к возникновению новых фаз и качественно меняет свойства системы, такие как когерентность и энергия. Таким образом, понимание роли симметрии чётности является ключевым для контроля и управления квантовыми системами, а также для разработки новых квантовых технологий.

Релаксация спина, являясь следствием взаимодействия квантовой системы с окружающей средой, играет ключевую роль в процессе декогеренции. Это взаимодействие приводит к потере квантовой информации и постепенному переходу системы из состояния суперпозиции в классическое смешанное состояние. Более того, релаксация спина существенно изменяет энергетический ландшафт системы, приводя к появлению новых энергетических уровней и модификации существующих. В результате, динамика системы становится более сложной и подверженной влиянию внешних факторов, что необходимо учитывать при разработке и реализации квантовых технологий. Понимание механизмов спиновой релаксации позволяет разрабатывать стратегии по минимизации декогеренции и увеличению времени когерентности квантовых битов, что критически важно для построения надежных и эффективных квантовых устройств.

Понимание взаимосвязи между симметрией, релаксацией спина и диссипацией имеет решающее значение для эффективного управления и манипулирования квантовыми системами. Взаимодействие этих факторов определяет динамику квантовых состояний и их чувствительность к внешним воздействиям. Например, нарушение симметрии вследствие диссипации может приводить к появлению новых состояний и переходам между ними, что используется в квантовых технологиях для создания когерентных состояний и управления квантовыми битами. Релаксация спина, хотя и является источником декогеренции, может быть использована для селективного подавления нежелательных квантовых состояний и оптимизации производительности квантовых устройств. Таким образом, контроль над этими процессами открывает возможности для создания более стабильных и эффективных квантовых систем, что крайне важно для развития квантовых вычислений, сенсоров и коммуникаций. Изучение этих взаимодействий позволяет точно настраивать параметры системы и добиваться желаемого поведения, что является ключевым фактором в реализации перспективных квантовых технологий.

В рамках приближения среднего поля сильные возмущения приводят к эволюции стационарных решений в нормальной (a) и симметрически сломанной (b) фазах, демонстрируя изменение порядка при различных начальных условиях.
В рамках приближения среднего поля сильные возмущения приводят к эволюции стационарных решений в нормальной (a) и симметрически сломанной (b) фазах, демонстрируя изменение порядка при различных начальных условиях.

Исследование, представленное в данной работе, раскрывает фундаментальную нестабильность суперрадиационной фазы в диссипативной модели Квази-Раби. Подобно тому, как течение времени неизбежно вносит изменения в любую систему, суперрадиация оказывается подвержена влиянию спиновой релаксации, что приводит к конечному времени жизни даже в пределе термодинамического равновесия. Эрвин Шрёдингер однажды заметил: «Всё, что мы называем реальностью, — это, по сути, лишь иллюзия, порожденная нашим разумом». Эта мысль перекликается с обнаруженной метастабильностью, указывая на то, что даже кажущиеся стабильными квантовые состояния могут быть лишь временными проявлениями более глубокой динамики. Понимание этих процессов, особенно с учетом влияния диссипативных эффектов, открывает новые горизонты в изучении открытых квантовых систем и их поведения во времени.

Куда же дальше?

Представленная работа, выявляя метастабильность суперрадиационной фазы в диссипативной модели Раби, лишь обнажает фундаментальную истину: любая система, даже квантовая, подвержена старению. Неизбежность распада, обусловленная спиновым релаксом, демонстрирует, что «долговечность» — это иллюзия, а не абсолютная характеристика. Каждый «баг» в этой динамике — момент истины на временной кривой, указывающий на внутреннюю хрупкость даже самых, казалось бы, устойчивых состояний.

Очевидным направлением дальнейших исследований представляется более детальное изучение природы «Лиувилловского зазора» и его влияния на скорость распада суперрадиационной фазы. Необходимо выйти за рамки приближения кумулянтного разложения, чтобы понять, как квантовые корреляции и флуктуации влияют на стабильность метастабильных состояний. По сути, требуется построить карту уязвимостей этой системы, выявляя критические точки, в которых даже незначительные возмущения могут привести к катастрофическому распаду.

В конечном счете, эта работа напоминает о том, что «технический долг» в квантовых системах — это не просто абстрактная концепция, а закладка прошлого, которую приходится оплачивать настоящим. Понимание механизмов, лежащих в основе метастабильности, позволит не только предсказывать время жизни квантовых состояний, но и разрабатывать стратегии для их продления — или, по крайней мере, для достойного старения.

Оригинал статьи: https://arxiv.org/pdf/2511.21508.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2025-11-29 14:31