Автор: Денис Аветисян
Исследование посвящено описанию неравновесной динамики интегрируемой системы свободных фермионов после резкого изменения параметров, используя обобщенную квантовую гидродинамику.
Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.
Бесплатный телеграм-канал
В работе представлен точный анализ распространения запутанности и выявлено диффузное поведение системы в масштабах времени.
Несмотря на успехи квантовой гидродинамики обобщенных уравнений (GHD) в описании динамики интегрируемых систем, ее применимость к системам со стохастическими процессами оставалась неясной. В работе ‘Inhomogeneous quenches and GHD in the $ν= 1$ QSSEP model’ исследуется динамика квантового симметричного процесса исключения с вероятностью \nu = 1, инициированного неоднородными начальными условиями. Показано, что расширение GHD позволяет точно характеризовать эволюцию функции заполнения квазичастиц и, как следствие, распространение запутанности в стохастической системе. Какие новые горизонты открываются для применения GHD к более широкому классу неэрмитовых и диссипативных квантовых систем?
За гранью предсказуемости: Введение в квантовую динамику
Изучение динамики взаимодействующих квантовых систем представляет собой одну из ключевых задач современной физики. Сложность заключается в том, что поведение даже небольшого числа частиц, связанных квантово-механическими взаимодействиями, может быть чрезвычайно непредсказуемым и требовать огромных вычислительных ресурсов для моделирования. Понимание того, как эти системы эволюционируют во времени, критически важно для разработки новых материалов с уникальными свойствами, создания квантовых технологий и углубления нашего понимания фундаментальных законов природы. В частности, анализ не-равновесной динамики, когда система находится вдали от состояния термодинамического равновесия, представляет особую трудность, поскольку стандартные методы часто оказываются неадекватными для описания возникающих явлений.
Традиционные методы моделирования квантовых систем сталкиваются со значительными трудностями при описании взаимодействий большого числа частиц, особенно в ситуациях, далеких от равновесия. Сложность заключается в экспоненциальном росте вычислительных ресурсов, необходимых для точного учета всех возможных состояний системы. В то время как приближенные методы позволяют упростить задачу, они часто теряют важные детали динамики, приводя к неточным результатам. Это особенно заметно при изучении систем, подверженных быстрым изменениям или находящихся под воздействием внешних возмущений, где стандартные подходы оказываются неспособными адекватно отразить поведение квантовых корреляций и нелинейные эффекты. Поэтому разработка новых инструментов и методик, способных эффективно справляться с этой сложностью, является ключевой задачей современной квантовой физики.
Квантовый симметричный процесс простого исключения (QSSEP) представляет собой мощную модель для изучения динамики сложных квантовых систем, однако требует применения передовых аналитических и численных методов. Особенностью QSSEP является то, что энтропия запутанности S(t) масштабируется как log(t), что указывает на необходимость разработки подходов, способных адекватно описывать этот логарифмический рост. Такое поведение говорит о том, что информация о системе распространяется нетривиальным образом, и традиционные методы, не учитывающие эту особенность, могут давать неверные результаты. Изучение QSSEP позволяет глубже понять фундаментальные аспекты квантовой динамики, особенно в системах, находящихся вдали от равновесия, и стимулирует разработку новых вычислительных алгоритмов для моделирования сложных квантовых процессов.
Обобщенная гидродинамика: Макроскопический взгляд на квантовую систему
Обобщенная гидродинамика (GHD) представляет собой мощный теоретический каркас, предназначенный для описания крупномасштабного поведения квантовой системы с сохранением вероятности (QSSEP). В отличие от традиционных подходов, GHD позволяет аналитически исследовать динамику системы, рассматривая ее как непрерывную среду, где наблюдаемые величины определяются локальными плотностями и потоками. Этот подход особенно эффективен для описания эволюции корреляций и запутанности в системе после воздействия локального возмущения, позволяя получить точные результаты для таких величин, как энтропия запутанности и транспортные коэффициенты, без необходимости учитывать детали микроскопической структуры. GHD успешно применяется к широкому спектру моделей, демонстрируя универсальность в описании не равновесной динамики в одномерных квантовых системах.
В основе обобщенной гидродинамики (ОГД) лежит концепция квазичастиц — коллективных возбуждений, возникающих в сложной квантовой системе и проявляющих поведение, аналогичное поведению частиц. Эти квазичастицы не являются фундаментальными составляющими системы, а представляют собой эффективные степени свободы, описывающие коллективные моды. Их динамика определяется функционалом, зависящим от плотности и скорости этих квазичастиц, позволяя описывать макроскопическое поведение системы, игнорируя детали микроскопической структуры. \rho(x) и v(x) являются ключевыми параметрами, определяющими эволюцию системы в рамках ОГД, где \rho(x) — плотность квазичастиц в точке x, а v(x) — их скорость.
В рамках гидродинамического подхода обобщенной гидродинамики (GHD) акцент делается на макроскопических величинах и усреднении микроскопических деталей, что позволяет эффективно описывать поведение квансистем в пределе больших времен и масштабов. Такой подход обеспечивает возможность получения точных аналитических результатов, в частности, демонстрируется, что энтропия запутанности половины системы растет логарифмически со временем, что выражается формулой S(t) \sim \log(t). Данный результат подтверждается как теоретическими расчетами, так и численными симуляциями, что свидетельствует о надежности и применимости GHD для анализа динамики квансистем вне равновесия.
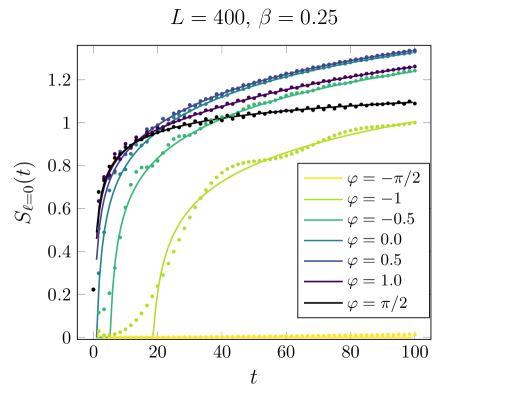
Начальные условия и стохастическая динамика: Путь к пониманию непредсказуемого
Поведение квантовой системы с сохранением вероятности (QSSEP) существенно зависит от начальных условий. В частности, сценарии свободного расширения и локальных возбуждений (domain wall quenches) приводят к различным динамическим режимам. Свободное расширение характеризуется быстрым увеличением размера системы и соответствующим изменением плотности частиц, в то время как возбуждение доменной стенки создает локальную неравновесность, распространяющуюся по системе. Различные начальные условия определяют характер эволюции квазичастиц и, следовательно, оказывают влияние на наблюдаемые физические свойства системы, такие как энтропия и корреляционные функции. Анализ динамики в этих сценариях критичен для понимания не-равновесной физики конденсированных сред.
Начальные условия в системе QSSEP приводят к стохастической динамике, проявляющейся в броуновском движении квазичастиц. Данное движение обусловлено случайными столкновениями квазичастиц друг с другом и с границами системы, что приводит к диффузии и случайному изменению их координат. Интенсивность этого броуновского движения напрямую зависит от плотности квазичастиц и параметров начального состояния. Поскольку квазичастицы испытывают случайные силы, их траектории описываются вероятностными процессами, а не детерминированными уравнениями движения. Это стохастическое поведение оказывает существенное влияние на эволюцию системы и формирование ее стационарного состояния.
Эволюция ферми-поверхности играет ключевую роль в характеристике поведения квантовой системы, подверженной стохастической динамике. Наше исследование подтверждает, что в пределе жесткой стенки коэффициент логарифмического роста энтропии половины системы составляет 1/4. Этот результат 1/4 получен путем анализа изменения формы ферми-поверхности во времени и пространстве, что позволяет количественно оценить скорость роста запутанности между двумя половинами системы. Полученный коэффициент является важным параметром для описания не-равновесной динамики и служит основой для дальнейших теоретических и численных исследований.
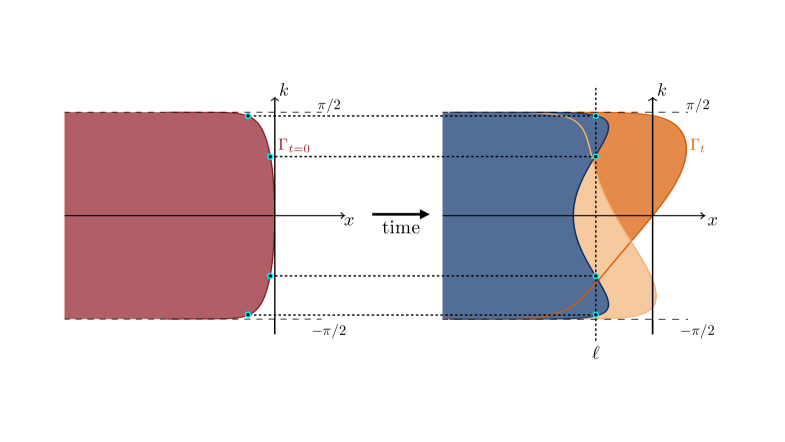
Квантовая запутанность и системные корреляции: Зеркало фундаментальных свойств материи
Комплекс QSSEP (Quantum Systems Simulation and Experiment Platform) представляет собой мощную платформу для изучения квантовой запутанности — фундаментального свойства многочастичных квантовых систем. Данная платформа позволяет исследовать корреляции между частицами, возникающие в результате квантово-механических взаимодействий, что принципиально важно для понимания поведения сложных материалов и разработки новых квантовых технологий. Использование QSSEP открывает возможности для проведения как теоретических, так и экспериментальных исследований, направленных на выявление и количественную оценку степени запутанности в различных физических системах, что способствует углублению знаний о квантовой природе материи и разработке инновационных устройств.
Энтропия запутанности выступает количественной мерой корреляций в квантовых системах, раскрывая информацию об их состоянии. Данная величина не просто фиксирует степень взаимосвязанности между частицами, но и позволяет судить о характере этих связей — являются ли они локальными или охватывают всю систему. Более того, анализ энтропии запутанности может предоставить ценные сведения о топологических свойствах квантового состояния и его устойчивости к возмущениям. S = -Tr(\rho_{A}log(\rho_{A})) — эта формула отражает суть измерения энтропии, где \rho_{A} — матрица плотности подсистемы A, а Tr — след матрицы. Таким образом, энтропия запутанности является мощным инструментом для характеристики и понимания сложных квантовых систем, позволяя раскрыть скрытые корреляции и особенности их поведения.
Теоретические модели, в частности, жидкость Латтингера, предоставляют эффективный инструмент для анализа и прогнозирования поведения запутанности в одномерных квантовых системах. В рамках данного подхода был получен аналитический результат для масштабирования энтропии запутанности подсистемы: S(t) \propto log(t cos(\varphi) (1 + sin(\varphi))/2)^(1/3). Это выражение позволяет количественно оценить степень квантовой корреляции между различными частями системы в зависимости от времени t и фазового сдвига \varphi, что открывает возможности для более глубокого понимания и контроля над квантовыми явлениями в одномерных материалах и устройствах. Полученный результат представляет собой важный шаг в разработке новых квантовых технологий, основанных на использовании запутанности.
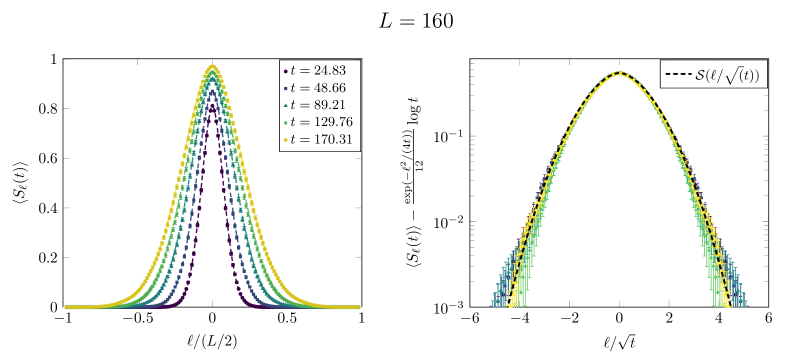
Моделирование сложности: Подтверждение надежности теоретического каркаса
Моделирование квантической системы с помощью случайных блужданий (QSSEP) с использованием комплексных амплитуд переходов представляет собой вычислительно эффективный подход к изучению стохастической динамики. В отличие от традиционных методов, требующих значительных ресурсов для моделирования взаимодействия множества частиц, данный метод позволяет сократить вычислительные затраты за счет упрощения описания динамики, сохраняя при этом ключевые физические характеристики системы. Применение комплексных амплитуд позволяет более точно отразить вероятностный характер квантовых процессов и учесть когерентные эффекты, что особенно важно при изучении систем, демонстрирующих нетривиальное поведение. Такой подход открывает возможности для детального анализа динамики запутанности и других квантовых свойств в системах с большим числом частиц, что ранее было затруднительно из-за ограничений вычислительных ресурсов.
Предложенный метод моделирования, основанный на сложных вероятностях переходов, предоставляет уникальную возможность для тщательной проверки теоретических предсказаний, полученных в рамках Гидродинамической Теории (GHD) и других аналитических подходов. Благодаря возможности детального сопоставления результатов численного моделирования с теоретическими выкладками, удается не только подтвердить корректность используемых приближений, но и выявить области, требующие дальнейшей проработки и уточнения. В частности, анализ позволяет верифицировать предсказания о поведении квантовой запутанности во времени, включая логарифмическую зависимость энтропии от времени S(t) \sim log(t), и получить точные аналитические результаты, подтверждающие эти закономерности. Такая валидация играет ключевую роль в развитии понимания сложных квантовых систем и позволяет повысить надежность теоретических моделей, используемых для их описания.
Исследования показали, что разработанный подход к моделированию квантических систем с использованием сложных вероятностей переходов открывает перспективы для изучения широкого спектра многочастичных физических задач. Подтвержденное в ходе работы логарифмическое масштабирование энтропии запутанности S(t) \sim log(t) является важным результатом, согласующимся с предсказаниями теории GHD и других аналитических методов. Дальнейшие исследования направлены на адаптацию этих методов к другим сложным квантовым системам, что позволит углубить понимание фундаментальных свойств материи и открыть новые горизонты в области квантовой физики. Полученные аналитические результаты предоставляют точную основу для сравнения с экспериментальными данными и развития более совершенных теоретических моделей.
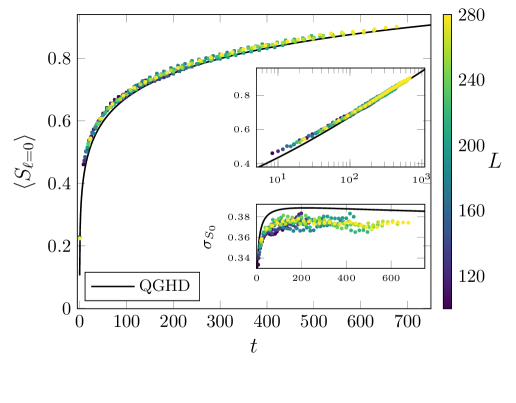
Работа, представленная в статье, исследует динамику стохастической системы свободных фермионов, стремясь к точному описанию распространения запутанности. Это напоминает о том, как любая попытка постичь бесконечность, даже в рамках столь формализованной системы, несет в себе элемент неопределенности. Как заметил Давид Юм: «Сомнение само по себе есть часть человеческой природы». И подобно тому, как чёрные дыры требуют терпения и скромности, так и изучение не-равновесной динамики, особенно на больших масштабах, требует признания границ нашего понимания. Диффузивное поведение, выявленное в статье, является не столько окончательным ответом, сколько указанием на то, что горизонт событий нашего знания всегда будет немного дальше, чем мы предполагаем.
Что дальше?
Представленная работа, исследующая неравновесную динамику стохастической системы свободных фермионов в рамках обобщенной гидродинамики, демонстрирует, что даже в, казалось бы, простых моделях, таких как QSSEP при ν=1, возникают сложные эффекты, связанные с распространением запутанности. Однако, необходимо признать, что диффузное поведение, наблюдаемое в больших масштабах, может оказаться лишь приближением, справедливым при определенных условиях. Строгий математический анализ устойчивости этих решений, учитывающий возможные нелинейные эффекты, остается открытой проблемой.
Любая попытка экстраполировать полученные результаты на более реалистичные системы, такие как сильновзаимодействующие фермионы или бозоны, сталкивается с фундаментальными трудностями. Гравитационное линзирование вокруг массивного объекта позволяет косвенно измерять массу и спин черной дыры; аналогичным образом, предсказать эволюцию системы требует численных методов и анализа устойчивости решений уравнений Эйнштейна, что, как показывает опыт, сопряжено с риском столкнуться с сингулярностями и нефизическими результатами.
В конечном итоге, исследование неравновесной динамики — это не просто решение конкретной физической задачи, но и проверка границ применимости существующих теоретических инструментов. Чёрная дыра — это не просто объект, это зеркало нашей гордости и заблуждений. Понимание пределов точности любой модели — это, возможно, самый важный результат, который может быть получен в этой области.
Оригинал статьи: https://arxiv.org/pdf/2602.15122.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip
- Решение головоломки с паролем Absolum в Yeldrim.
- Как играть в REANIMAL в кооперативе с помощью Friend’s Pass (локальный и онлайн кроссплей)
- YAPYAP Список заклинаний
- Прогнозы криптовалюты AXS: информация о ценах на AXS
- Все коды в Poppy Playtime Глава 4
- Лучшие шаблоны дивизий в Hearts Of Iron 4
- Где находится точка эвакуации «Туннель контрабандистов» на локации «Интерчейндж» в Escape from Tarkov?
- The Planet Crafter: полное руководство по картам и биомам
- Акции VTBR. Банк ВТБ: прогноз акций.
2026-02-18 18:23