Новые грани полудираковских фермионов: влияние кулоновского взаимодействия

Автор: Денис Аветисян

Исследование показывает, как долгодействующие кулоновские взаимодействия изменяют свойства полудираковских фермионов, открывая возможности для контроля плотности состояний и других ключевых физических параметров.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал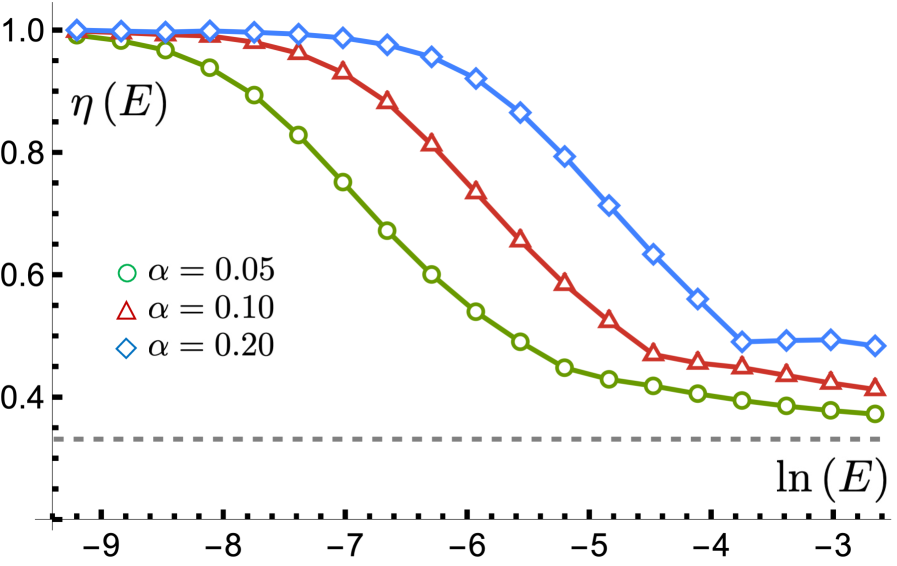

В рамках расчетов на уровне Хартри-Фока для системы с <span class="katex-eq" data-katex-display="false">g=1/2</span>, эволюция показателя степени <span class="katex-eq" data-katex-display="false">\eta(E)</span> в плотности состояний <span class="katex-eq" data-katex-display="false">\rho(E) \sim E^{\eta(E)}</span> демонстрирует плавный переход от линейного дираковского поведения (<span class="katex-eq" data-katex-display="false">\eta=1</span>) при низких энергиях к полудираковскому поведению типа II (<span class="katex-eq" data-katex-display="false">\eta=1/3</span>) при увеличении энергии, что отражает изменение взаимодействующего спектра, представленное на рисунке 3, и зависит от силы взаимодействия α (0.05, 0.10, 0.20). — В рамках расчетов на уровне Хартри-Фока для системы с $g=1/2$ , эволюция показателя степени $\eta(E)$ в плотности состояний $\rho(E) \sim E^{\eta(E)}$ демонстрирует плавный переход от линейного дираковского поведения ( $\eta=1$ ) при низких энергиях к полудираковскому поведению типа II ( $\eta=1/3$ ) при увеличении энергии, что отражает изменение взаимодействующего спектра, представленное на рисунке 3, и зависит от силы взаимодействия α (0.05, 0.10, 0.20).

В данной работе исследуется влияние кулоновского взаимодействия на свойства типа-II полудираковских фермионов с использованием ренормализационной группы и теории функционала плотности.

В рамках изучения топологических фаз материи, квазичастицы с необычными свойствами привлекают особое внимание. Настоящая работа, посвященная исследованию ‘Interacting type-II semi-Dirac quasiparticles’, анализирует влияние кулоновских взаимодействий на поведение полудираковских фермионов второго типа в двумерных гетероструктурах. Показано, что взаимодействие приводит к эволюции спектра от анизотропной дираковской дисперсии к характерной форме «бумеранга», изменяя плотность состояний от линейной до степенной ( $\sim |\varepsilon|^{1/3}$ ) зависимости и модифицируя энергетическую зависимость физических величин, таких как уровни Ландау. Каким образом подобные взаимодействия могут быть использованы для создания новых материалов с управляемыми топологическими свойствами и необычными транспортными характеристиками?

Погоня за Элегантностью: От Кремния к Полудиракам

Традиционные электронные материалы, такие как кремний, несмотря на свою повсеместность, часто оказываются недостаточно гибкими для реализации новых, сложных функций в современной электронике. Ограничения в масштабируемости, энергоэффективности и способности адаптироваться к различным условиям эксплуатации становятся все более заметными. Эти материалы демонстрируют фиксированные электронные свойства, что затрудняет создание устройств с программируемыми или динамически изменяемыми характеристиками. Потребность в материалах, способных преобразовывать и контролировать поток электронов более эффективно, стимулирует поиск альтернативных подходов и новых квазичастиц, способных преодолеть эти ограничения и открыть путь к более продвинутым электронным устройствам.

Полупроводниковые материалы нового поколения могут быть основаны на квазичастицах, известных как полудирак-фермионы. Эти уникальные объекты представляют собой нечто среднее между безмассовыми (как фотоны) и массивными (как электроны) частицами, демонстрируя необычные электронные свойства. В отличие от традиционных электронов, поведение полудирак-фермионов описывается модифицированным уравнением Дирака, что приводит к линейной дисперсии энергии лишь в одном направлении и квадратичной — в другом. $E(k) \propto \sqrt{k_x^2}k_y$ Эта асимметрия открывает возможности для создания устройств с улучшенными характеристиками, например, с повышенной подвижностью носителей заряда и уникальными оптическими свойствами. Изучение и контроль над полудирак-фермионами может привести к разработке более эффективных транзисторов, сенсоров и других электронных компонентов, преодолевающих ограничения существующих технологий.

Понимание механизмов возникновения и возможности управления полудираковскими фермионами является ключевым фактором для создания принципиально новых электронных устройств. Эти квазичастицы, находящиеся на грани между безмассовыми и массивными состояниями, обладают уникальными транспортными свойствами, позволяющими преодолеть ограничения традиционных полупроводников. Исследования направлены на разработку материалов и структур, в которых полудираковские фермионы проявляются наиболее ярко и могут быть контролируемыми внешними воздействиями, такими как электрическое поле или деформация. Возможность точной настройки характеристик этих фермионов открывает перспективы для создания сверхбыстрых и энергоэффективных транзисторов, а также новых типов сенсоров и квантовых устройств, работающих на основе $spintronics$ и топологической электроники.

Функция статической поляризации для полудираковских фермионов типа II демонстрирует разделение областей доминирования зависимости от <span class="katex-eq" data-katex-display="false">p_x^{\sqrt{p_x}}</span> и <span class="katex-eq" data-katex-display="false">p_y^{1/3}</span>, разделенных «ущельем» на <span class="katex-eq" data-katex-display="false">p_y = (c_1/c_2)^3 p_x^{3/2}</span>, что подтверждается структурой линий постоянных <span class="katex-eq" data-katex-display="false">p_x</span> и <span class="katex-eq" data-katex-display="false">p_y</span> при <span class="katex-eq" data-katex-display="false">c_1 = 0.196\pi</span>, <span class="katex-eq" data-katex-display="false">c_2 = 0.154\pi</span> и <span class="katex-eq" data-katex-display="false">w = 50</span>. — Функция статической поляризации для полудираковских фермионов типа II демонстрирует разделение областей доминирования зависимости от $p_x^{\sqrt{p_x}}$ и $p_y^{1/3}$ , разделенных «ущельем» на $p_y = (c_1/c_2)^3 p_x^{3/2}$ , что подтверждается структурой линий постоянных $p_x$ и $p_y$ при $c_1 = 0.196\pi$ , $c_2 = 0.154\pi$ и $w = 50$ .

Двухслойный Графен: Платформа для Экзотических Фермионов

Двухслойный графен является благоприятной средой для возникновения полудираковских фермионов благодаря своей уникальной зонной структуре. В отличие от однослойного графена, где линейное дисперсионное соотношение приводит к дираковским фермионам, взаимодействие между слоями в двуслойном графене приводит к модификации зонной структуры. Это проявляется в появлении двух различных зон проводимости и валентности, которые пересекаются в точках, отличных от точек $K$ и $K'$ в зоне Бриллюэна. В результате, электронные состояния вблизи этих точек демонстрируют линейное, но асимметричное дисперсионное соотношение, характерное для полудираковских фермионов, что отличает их от стандартных дираковских фермионов и обуславливает специфические электронные и транспортные свойства материала.

Механизм скольжения слоев в двуслойном графене представляет собой эффективный способ настройки электронных свойств материала и индуцирования поведения, характерного для полудираковских фермионов. Смещение слоев относительно друг друга изменяет перекрывание $p_z$ орбиталей атомов углерода, что приводит к модификации энергетической дисперсии и, как следствие, к изменению электронной структуры. Этот эффект позволяет контролировать ширину запрещенной зоны и эффективную массу носителей заряда, что делает механизм скольжения перспективным для создания устройств с настраиваемыми электронными характеристиками. Величина и направление смещения слоев напрямую влияют на параметры полудираковских фермионов, такие как линейность дисперсионной зависимости и скорость их распространения.

Для точного моделирования характеристик фермионов, возникающих при реализации механизма межслойного скольжения в двуслойном графене, необходимо детальное понимание гамильтониана системы. Гамильтониан, описывающий энергию и взаимодействие электронов в структуре, включает в себя кинетическую энергию, потенциальную энергию, обусловленную структурой графена, и члены, учитывающие взаимодействие между слоями. $H = H_0 + V_{int}$ , где $H_0$ — кинетическая энергия, а $V_{int}$ — потенциал взаимодействия. Учет специфики потенциала взаимодействия, включая межслойные переходы и влияние внешних полей, критически важен для корректного расчета энергии и волновых функций фермионов, а также для прогнозирования наблюдаемых электронных свойств.

Изменение параметра Δ в гамильтониане <span class="katex-eq" data-katex-display="false">\mathcal{H}=\left(g_{1}k_{x}^{2}-vk_{y}+\Delta\right)\hat{\sigma}_{x}+g_{2}k_{x}k_{y}\hat{\sigma}_{y}</span> приводит к различным типам дираковских конусов: при <span class="katex-eq" data-katex-display="false">\Delta<0</span> наблюдается три конуса в точках <span class="katex-eq" data-katex-display="false">(0,\Delta/v), (\pm\sqrt{-\Delta g_{1}},0)</span>, при <span class="katex-eq" data-katex-display="false">\Delta=0</span> они объединяются в полудирактовскую точку с ненулевой фазой Берри, а при <span class="katex-eq" data-katex-display="false">\Delta>0</span> происходит сдвиг точек пересечения и наблюдается полудирактовское поведение при высоких энергиях. — Изменение параметра Δ в гамильтониане $\mathcal{H}=\left(g_{1}k_{x}^{2}-vk_{y}+\Delta\right)\hat{\sigma}_{x}+g_{2}k_{x}k_{y}\hat{\sigma}_{y}$ приводит к различным типам дираковских конусов: при $\Delta<0$ наблюдается три конуса в точках $(0,\Delta/v), (\pm\sqrt{-\Delta g_{1}},0)$ , при $\Delta=0$ они объединяются в полудирактовскую точку с ненулевой фазой Берри, а при $\Delta>0$ происходит сдвиг точек пересечения и наблюдается полудирактовское поведение при высоких энергиях.

Теоретический Арсенал: Учет Взаимодействий и Перенормировка Спектра

В двуслойном графене кулоновское взаимодействие между электронами оказывает существенное влияние на энергетический спектр, приводя к его перенормировке. Данное взаимодействие, обусловленное электростатическим отталкиванием между зарядами, изменяет дисперсионное соотношение, отклоняя его от идеальной линейной зависимости. Перенормировка спектра проявляется в изменении эффективной массы носителей заряда и введении дополнительных энергетических масштабов. Изменения в спектре приводят к модификации плотности состояний и, как следствие, к изменению оптических и транспортных свойств материала. В частности, перенормировка спектра влияет на величину запрещенной зоны и на подвижность носителей заряда, определяя электронные характеристики двуслойного графена.

Для учета сложных кулоновских взаимодействий между электронами в бислойном графене используется комбинированный подход, включающий теорию возмущений, экранирование в рамках приближения случайных фаз (RPA) и функцию поляризации. Теория возмущений позволяет аппроксимировать влияние взаимодействий на электронный спектр, в то время как RPA-экранирование учитывает ослабление кулоновского взаимодействия за счет коллективных возбуждений электронов. Функция поляризации, описывающая отклик электронной системы на внешнее поле, необходима для корректного вычисления экранированного кулоновского взаимодействия и, следовательно, для точного определения спектральных характеристик материала. Такой метод обеспечивает надежный инструмент для анализа и прогнозирования изменений в плотности состояний и других ключевых электронных свойствах бислойного графена.

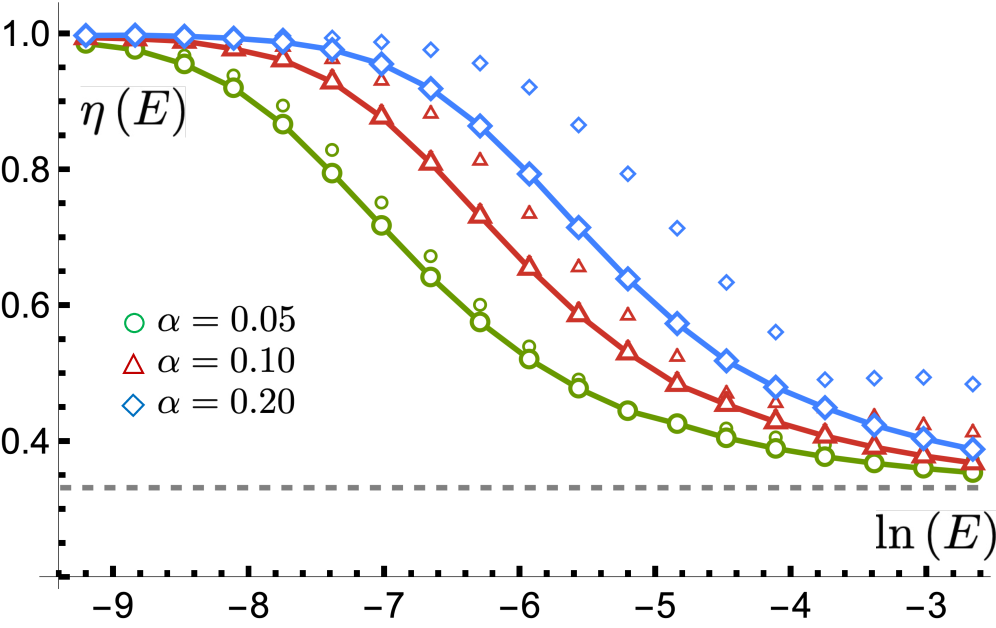
Расчеты плотности состояний (Density of States, DOS) для двуслойного графена, выполненные с использованием теории возмущений, демонстрируют изменение зависимости от энергии. При низких энергиях наблюдается линейная зависимость $η=1$ , что соответствует стандартному поведению. Однако, с увеличением энергии зависимость переходит к степенному закону $η=1/3$ . Данное изменение DOS оказывает существенное влияние на электронные свойства материала, подтверждая его полудираковское поведение и согласуясь с экспериментальными данными. Изменение характера зависимости DOS является прямым следствием экранирования кулоновского взаимодействия между электронами, учитываемого в рамках приближения случайных фаз (Random Phase Approximation, RPA).

Анализ плотности состояний <span class="katex-eq" data-katex-display="false">\eta(E)</span> в рамках взаимодействия Кулона, экранированного RPA, показывает ослабление ренормализации при увеличении параметров α (0.05, 0.10, 0.20), что подтверждается сравнением с результатами Hartree-Fock, демонстрирующими независимость от α. — Анализ плотности состояний $\eta(E)$ в рамках взаимодействия Кулона, экранированного RPA, показывает ослабление ренормализации при увеличении параметров α (0.05, 0.10, 0.20), что подтверждается сравнением с результатами Hartree-Fock, демонстрирующими независимость от α.

Тип II: Полудираки с Фазой Берри и Топологическими Подписями

Получение полудираковских фермионов типа II, возникающих в результате слияния дираковских конусов, связано с проявлением конечной фазы Берри — фундаментальной топологической характеристики. Данное явление указывает на нетривиальную геометрическую структуру электронных состояний, определяющую их устойчивость к внешним воздействиям и обеспечивающую уникальные транспортные свойства. Фаза Берри, приобретая ненулевое значение, обуславливает появление аномальных эффектов, таких как аномальный эффект Холла, и играет ключевую роль в формировании топологически защищенных состояний, что делает эти фермионы перспективными кандидатами для реализации инновационных электронных устройств и спинтроники. Изучение фазы Берри позволяет глубже понять топологические свойства материалов и использовать их для создания принципиально новых функциональных материалов.

Недавние экспериментальные исследования подтвердили существование полудираковских фермионов типа II в гетероструктурах оксида титана и ванадия. Данное открытие имеет принципиальное значение, поскольку демонстрирует возможность реализации этих экзотических состояний вещества в реальных материалах, открывая перспективы для создания инновационных устройств. В частности, уникальные электронные свойства этих фермионов, обусловленные их необычной дисперсией, позволяют надеяться на разработку новых поколений спинтронных приборов с повышенной эффективностью и функциональностью. Исследователи полагают, что контроль над свойствами гетероструктур позволит точно настраивать характеристики фермионов, оптимизируя их для конкретных применений в области электроники и материаловедения.

Число Черна, являясь топологическим инвариантом, характеризует состояние полудираковских фермионов типа II и подтверждает их устойчивость к возмущениям, что делает их перспективными для использования в спинтронных устройствах. В отличие от традиционных систем типа I, в этих материалах наблюдается отклонение в масштабировании уровней Ландау, которое подчиняется зависимости $\propto (nB)^{1/(\eta+1)}$ , где $n$ — концентрация носителей, $B$ — магнитное поле, а η — показатель степени плотности состояний. Данная зависимость указывает на то, что управление этими параметрами позволит тонко настраивать электронные свойства материалов на основе квартичных полудираковских фермионов, открывая возможности для создания инновационных устройств с улучшенными характеристиками и функциональностью.

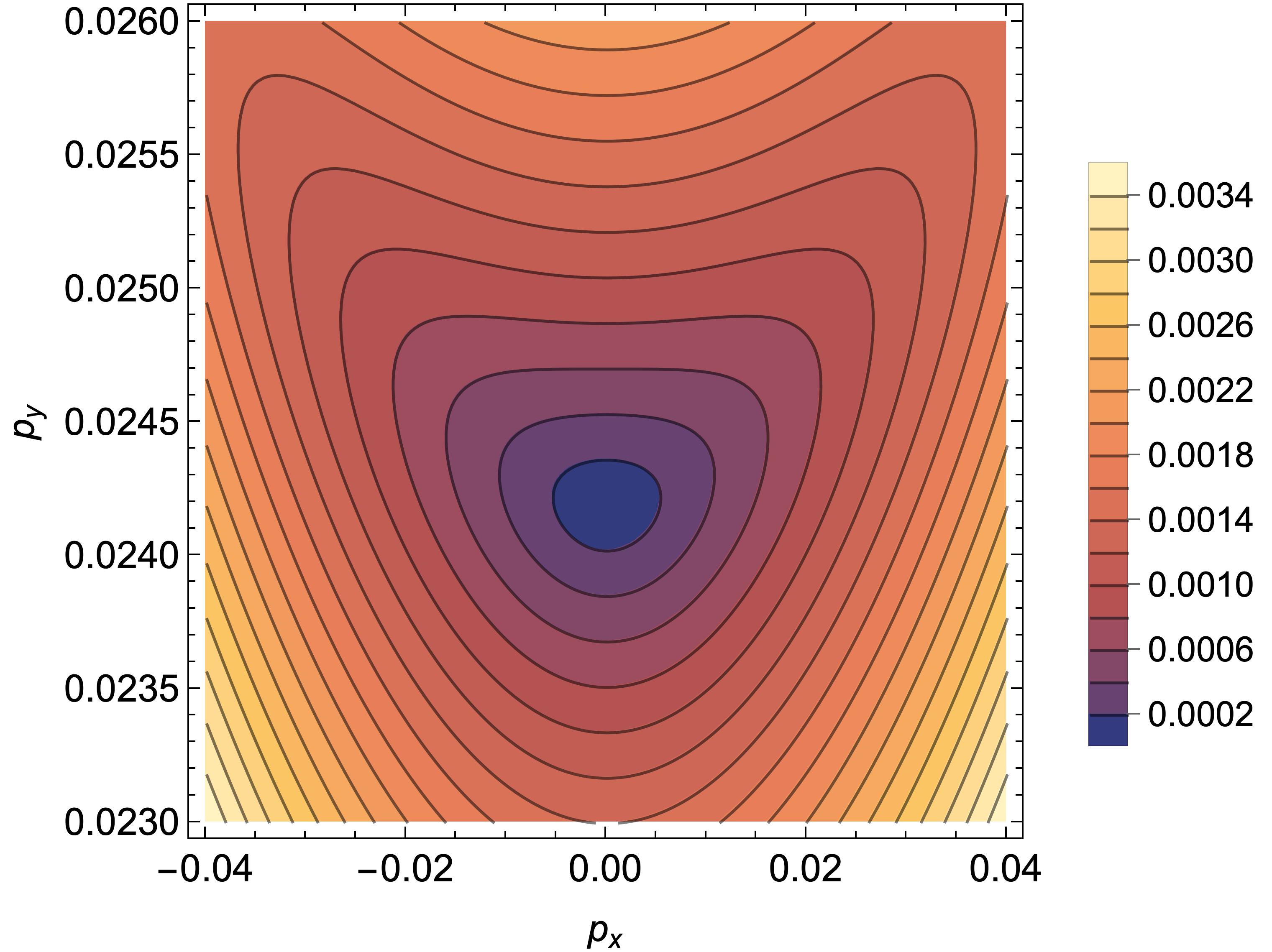
При расчете спектра типа II, нормированного на кулоновское взаимодействие в цикле Хартри-Фока при <span class="katex-eq" data-katex-display="false">\alpha = 0.2</span> и <span class="katex-eq" data-katex-display="false">g = 1/2</span>, наблюдается анизотропный дираковский конус, подтвержденный вогнутым полудираковским поведением при более высоких энергиях, что соответствует уравнению (10) и значениям <span class="katex-eq" data-katex-display="false">\Delta/\varepsilon_0 = 1.88/4\pi</span> и <span class="katex-eq" data-katex-display="false">c/v = 1.39/4\pi</span> при ультрафиолетовом обрезании импульса <span class="katex-eq" data-katex-display="false">|k_{\Lambda}^{x,y}| = 1.1</span>. — При расчете спектра типа II, нормированного на кулоновское взаимодействие в цикле Хартри-Фока при $\alpha = 0.2$ и $g = 1/2$ , наблюдается анизотропный дираковский конус, подтвержденный вогнутым полудираковским поведением при более высоких энергиях, что соответствует уравнению (10) и значениям $\Delta/\varepsilon_0 = 1.88/4\pi$ и $c/v = 1.39/4\pi$ при ультрафиолетовом обрезании импульса $|k_{\Lambda}^{x,y}| = 1.1$ .

Расширяя Горизонты: Квартичные Полудираки и Новые Возможности

Квартичные полудираковские фермионы представляют собой расширение стандартной полудираковской модели, в которой квадратичная дисперсия заменена полиномом более высокой степени. Данное обобщение позволяет значительно расширить возможности контроля над электронными свойствами материала. В то время как в классической полудираковской модели дисперсия описывается параболой, использование квартичного полинома вносит нелинейные поправки, изменяющие форму энергетических спектров. Это, в свою очередь, влияет на транспортные характеристики и топологические свойства системы, открывая путь к созданию устройств с улучшенными или принципиально новыми функциональными возможностями. Изменение степени полинома дисперсии позволяет тонко настраивать эффективную массу и скорость фермионов, что критически важно для разработки материалов с заданными электронными характеристиками.

Расширение стандартной модели полудираковских фермионов до квартичных форм предоставляет беспрецедентные возможности для управления электронными свойствами материалов. Замена квадратичной дисперсии на полином более высокой степени позволяет тонко настраивать поведение носителей заряда, что открывает путь к созданию устройств с принципиально новыми функциональными возможностями. Подобный контроль над электронной структурой позволяет оптимизировать характеристики полупроводников для конкретных применений, например, в высокочувствительных сенсорах или энергоэффективной электронике. Квартичные полудираковские фермионы, благодаря своей уникальной дисперсии, могут демонстрировать улучшенную подвижность носителей заряда и повышенную устойчивость к рассеянию, что критически важно для повышения производительности электронных устройств.

Понимание взаимосвязи между топологическими характеристиками, такими как число Черна, и динамической проводимостью является ключевым для раскрытия всего потенциала этих продвинутых квазичастиц. Исследования показывают, что удельная теплоёмкость масштабируется с температурой как $T^{(\eta+1)}$ , в то время как электронная сжимаемость зависит от плотности как $n^{-(\eta/(\eta+1))}$ . Данная зависимость указывает на то, что управление этими параметрами позволит тонко настраивать электронные свойства материалов на основе квартичных полудираковских фермионов, открывая возможности для создания инновационных устройств с улучшенными характеристиками и функциональностью. Изучение этой связи позволяет прогнозировать и контролировать поведение системы в различных условиях, что является необходимым шагом для практического применения этих уникальных квазичастиц.

Исследование взаимодействия типа-II полудираковских квазичастиц закономерно выявляет, что даже самые изящные теоретические конструкции сталкиваются с суровой реальностью кулоновских взаимодействий. Подобно тому, как в любой CI-системе, где молитвы о стабильности неизбежно терпят крах, и здесь долгорадиусные взаимодействия вносят свои коррективы в плотность состояний. Как отмечал Гегель: «Всё сущее рационально». Это, конечно, не означает, что всё понятно, а лишь то, что даже кажущийся хаос имеет свою логику, пусть и скрытую за сложными уравнениями и кулоновским экранированием. Попытки упростить жизнь, описывая системы в рамках идеальных моделей, лишь добавляют новый слой абстракции, который рано или поздно потребует исправления.

Что дальше?

Представленная работа, как и большинство теоретических построений, лишь аккуратно отодвинула завесу над очередным клубком вопросов. Рассматривая взаимодействие полудираковских квазичастиц второго типа, авторы столкнулись с неизбежной проблемой: долгодействующие кулоновские взаимодействия всегда найдут способ усложнить даже самую элегантную модель. Попытки «настроить» плотность состояний, конечно, интересны, но, как показывает опыт, любое вмешательство в базовые параметры системы порождает новые, часто непредсказуемые эффекты. Это не открытие — это закон сохранения сложности.

В дальнейшем, вероятно, потребуется более детальное исследование влияния анизотропии дираковской конусы на наблюдаемые физические величины. Но даже точное описание спектральных функций не решит фундаментальной проблемы: реальные материалы никогда не будут соответствовать идеализированным теоретическим моделям. Вместо того чтобы гоняться за «чистыми» полудираками, возможно, стоит обратить внимание на системы, где эти квазичастицы взаимодействуют с другими типами носителей заряда или магнитными моментами. Тогда, возможно, удастся создать нечто действительно новое, хотя бы на короткое время, прежде чем это превратится в очередной техдолг.

Очевидно, что попытки предсказать поведение таких систем при конечных температурах — это упражнение в оптимизме. Но даже в рамках нулевой температуры, «настройка» плотности состояний — это лишь первый шаг. В конечном итоге, важно понять, как эти полудираковские квазичастицы влияют на макроскопические свойства материалов — на их теплопроводность, электропроводность и магнитные свойства. И, конечно, на то, как быстро все это сломается.

Оригинал статьи: https://arxiv.org/pdf/2601.21098.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-01 15:30