От флорентийских экспериментов к фермионам: история статистики Ферми

Автор: Денис Аветисян

В статье реконструируется путь развития статистики Ферми-Дирака, начиная с ранних исследований моноатомных газов и вклада Энрико Ферми, и освещается ее значительное влияние на различные научные области.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал

Письмо, отправленное Ферми Дираку, запечатлено в истории науки, свидетельствуя о незримой нити, связывающей гениев в поисках истины и отражая личную переписку, ставшую частью фундаментальной физики.

Исторический анализ формирования квантовой статистики и ее роли в современной физике.

Несмотря на фундаментальную роль статистики Ферми-Дирака в современной физике, исторические корни ее формирования остаются недостаточно изученными. Данная работа, озаглавленная ‘From Florence to Fermions: a historical reconstruction of the origins of Fermi’s statistics one hundred years later’, реконструирует путь, приведший молодого Энрико Ферми к созданию его новаторской работы о статистике идеального моноатомного газа, опираясь на его ранний интерес к абсолютной энтропии и проблемах квантования в системах идентичных частиц. Ключевым шагом стало применение принципа Паули, первоначально сформулированного для электронов в атоме, к системе невзаимодействующих частиц, что позволило создать принципиально новую статистическую схему. Какие еще малоизвестные факторы и научные дискуссии способствовали появлению этой основополагающей теории, оказавшей влияние на широкий спектр областей, от физики полупроводников до астрофизики?

На заре квантовой статистики: от хаоса к порядку

В начале XX века физики столкнулись с серьезными трудностями в описании поведения частиц на микроскопическом уровне. Существующие классические модели оказывались неспособны объяснить наблюдаемые свойства материалов, такие как теплоемкость, проводимость и спектры излучения. Отсутствие адекватной теоретической базы препятствовало пониманию фундаментальных свойств вещества и создавало значительные препятствия для развития новых технологий. Например, классическая физика предсказывала, что теплоемкость твердых тел должна быть постоянной величиной, что явно противоречило экспериментальным данным. Это несоответствие, а также другие аномалии, указывали на необходимость разработки принципиально нового подхода к описанию поведения частиц, способного учитывать квантовые эффекты и статистические закономерности, управляющие их коллективным поведением.

В начале XX века классическая физика оказалась неспособна объяснить ряд наблюдаемых явлений, особенно поведение материи на микроскопическом уровне. Это несоответствие потребовало разработки новой теоретической базы — так называемой Старой Квантовой Теории. Хотя эта теория и представляла собой лишь временное, несовершенное решение, она стала необходимым шагом на пути к пониманию квантового мира. Несмотря на свои ограничения и противоречия, Старая Квантовая Теория позволила объяснить спектры излучения атомов и некоторые другие явления, открыв дорогу для последующего развития квантовой механики и формирования более полной и точной картины реальности. Она представляла собой смелую попытку примирить устоявшиеся представления о физике с новыми экспериментальными данными, заложив фундамент для будущих открытий.

В начале XX века, стремление понять поведение идентичных частиц стало ключевым в развитии квантовой статистики. Ученые столкнулись с необходимостью описать, как частицы, неразличимые друг от друга, распределяются по энергетическим уровням и влияют на свойства материи. Этот поиск привёл к осознанию, что классическая статистика здесь неприменима, и потребовал разработки нового подхода. Именно в этом контексте, работы Энрико Ферми, кульминировавшие в его публикации 1926 года, заложили основу для понимания поведения фермионов — частиц, подчиняющихся принципу Паули, запрещающему двум идентичным фермионам занимать одно и то же квантовое состояние. Эта работа не только объяснила свойства многих материалов, но и предопределила дальнейшее развитие квантовой механики и физики конденсированного состояния.

Здание Теваджино, первоначально принадлежавшее Институту геофизики, служило жильем для Расетти и Ферми, а также являлось базой для Лаборатории оптики и прецизионной механики, согласно материалам фонда имени Джорджо Ронки.

Революция Ферми: усмирение хаоса частиц

Энрико Ферми разработал новый статистический подход, предназначенный для описания фермионов — частиц, подчиняющихся принципу Паули. Существующие статистические методы, такие как классическая статистика Максвелла-Больцмана и статистика Бозе-Эйнштейна, не учитывали квантовую природу фермионов и их свойство не занимать одно и то же квантовое состояние. Принцип Паули, гласящий, что два фермиона не могут находиться в одном и том же квантовом состоянии одновременно, требовал разработки новой статистической модели, учитывающей это ограничение. Ферми-Дирак статистика, предложенная Ферми, корректно описывает распределение фермионов по энергетическим уровням, учитывая их неразличимость и принцип исключения, что позволило более точно рассчитать свойства систем, состоящих из фермионов, таких как электроны в металлах.

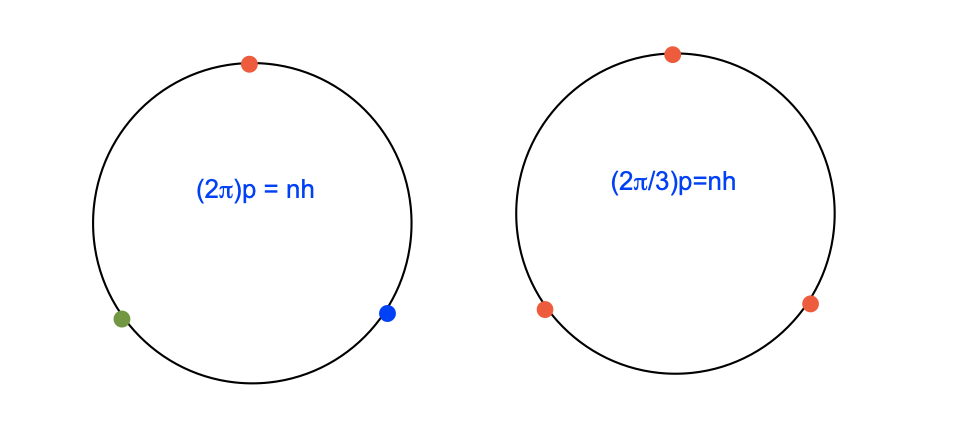
Метод Ферми для расчета распределения фермионов основывался на квантовании фазового пространства с использованием правил Зоммерфельда. В отличие от классической статистики, правила Зоммерфельда учитывают дискретность энергетических уровней, позволяя определить число состояний с энергией ниже определенного значения. Это квантование фазового пространства, где каждая точка представляет собой состояние с определенным импульсом и энергией, позволило Ферми вывести статистику, описывающую распределение фермионов в системе. По сути, $\in t_{0}^{\in fty} g(\epsilon) d\epsilon$ дает общее число состояний, а правила Зоммерфельда определяют, как энергия заполняет эти состояния, учитывая принцип Паули.

Метод Ферми стал развитием формулы Заккура-Тетрода, предоставляя более точное описание поведения частиц в системе. В то время как формула Заккура-Тетрода успешно описывала идеальные газы, она не учитывала квантовую природу частиц и принцип исключения Паули. Подход Ферми, использующий квантование Зоммерфельда в фазовом пространстве, позволил учесть эти факторы и получить более реалистичное распределение фермионов. Это привело к более точным предсказаниям свойств систем, состоящих из фермионов, таких как металлы и вырожденные звездные вещества, и позволило корректно описывать их теплоемкость и другие термодинамические свойства, которые ранее не могли быть объяснены классической статистикой.

Статистика Ферми, разработанная на основе квантования по Зоммерфельду, оказалась мощным инструментом для анализа свойств электронов и других фермионов. Неожиданно, первоначальная демонстрация эффективности метода произошла применительно к бозонным системам, в частности к гелию. Это позволило более точно рассчитать термодинамические свойства гелия при низких температурах, чем это было возможно с использованием классической статистики. Изначальное применение к бозонам подчеркнуло универсальность подхода Ферми и его способность описывать поведение частиц с различной статистикой, несмотря на то, что он был разработан для фермионов, подчиняющихся принципу Паули.

Правила квантования Зоммерфельда демонстрируют различие в допустимых состояниях для трёх различимых и трёх неразличимых частиц.

Применение к науке о материалах: от теории к практике

Статистика Ферми стала основополагающей для понимания поведения электронов в материалах, особенно в рамках модели электронного газа. В данной модели, электроны рассматриваются как фермионы, подчиняющиеся принципу Паули, что означает, что два электрона не могут находиться в одном и том же квантовом состоянии. Это приводит к заполнению энергетических уровней электронами, начиная с самых низких, и формированию μ — уровня Ферми, определяющего максимальную занятую энергию при абсолютном нуле температуры. При температурах выше абсолютного нуля, распределение электронов описывается функцией Ферми-Дирака, учитывающей вероятность занятия конкретного энергетического уровня электроном. Применение статистики Ферми позволяет корректно описывать такие свойства материалов, как теплоемкость, электропроводность и магнитные свойства, в отличие от классической статистики Максвелла-Больцмана, которая не учитывает квантовую природу электронов.

Уровень Ферми ( $E_F$ ) представляет собой энергетический уровень, при котором вероятность заполнения электроном равна 50% при заданной температуре. В рамках статистики Ферми-Дирака, этот уровень возникает как следствие принципа исключения Паули, запрещающего двум фермионам (в данном случае, электронам) находиться в одном и том же квантовом состоянии. В металлах и полупроводниках, уровень Ферми определяет распределение электронов по энергетическим уровням и, следовательно, влияет на электрические, тепловые и оптические свойства материала. Положение уровня Ферми относительно зон проводимости и валентности определяет тип проводимости материала (n-тип или p-тип) и его эффективность в качестве электронного компонента.

Статистика Ферми играет ключевую роль в понимании поведения полупроводников, материалов, являющихся основой современной электроники. В полупроводниках, в отличие от металлов и изоляторов, концентрация носителей заряда (электронов и дырок) определяется не только температурой, но и плотностью примесей и дефектов кристаллической решетки. Применение статистики Ферми позволяет точно рассчитать распределение электронов по энергетическим уровням в зоне проводимости и зоне валентности, что необходимо для определения таких характеристик полупроводников, как электропроводность, концентрация носителей заряда и ширина запрещенной зоны. $f(E) = \frac{1}{e^{(E-E_F)/kT} + 1}$ — функция Ферми-Дирака, описывающая вероятность заполнения энергетического уровня E при температуре T и уровне Ферми $E_F$ , является фундаментальным инструментом в анализе поведения электронов в полупроводниках и объясняет их уникальные электронные свойства.

Разработка статистической механики на основе принципов Ферми и Бозе позволила существенно расширить понимание фундаментальных свойств вещества, выйдя за рамки классической физики. Классическое описание, основанное на равновероятности всех состояний, оказалось неспособным объяснить поведение систем, состоящих из большого числа идентичных частиц с полуцелым или целым спином. Новая теория учитывает квантовую природу частиц и принцип Паули, согласно которому два фермиона не могут находиться в одном и том же квантовом состоянии. Это привело к объяснению таких явлений, как теплоёмкость металлов, которые в классической физике предсказывались неверными. Применение статистик Ферми и Бозе позволило точно рассчитать $E_F$ — энергию Ферми, определяющую распределение электронов в металлах и полупроводниках, а также поведение бозонов при низких температурах, что привело к предсказанию и экспериментальному подтверждению явления сверхпроводимости и конденсата Бозе-Эйнштейна.

За пределами обычного вещества: горизонты новых открытий

Статистика Ферми, фундаментальный принцип квантовой механики, объясняет поведение фермионов — частиц, обладающих полуцелым спином, таких как электроны. В рамках этой статистики, два электрона, несмотря на взаимное отталкивание, могут образовывать так называемые куперовские пары. Этот феномен обусловлен тем, что электроны, взаимодействуя через колебания кристаллической решетки, могут снизить свою общую энергию, формируя связанное состояние. $q = \hbar k$ Несмотря на электростатическое отталкивание, при определенных условиях — низких температурах и подходящем взаимодействии — энергия связи в куперовской паре превосходит силу отталкивания, приводя к образованию макроскопически когерентного состояния, необходимого для сверхпроводимости. Понимание этого механизма, основанного на статистике Ферми, открыло путь к изучению экзотических состояний материи и развитию передовых технологий.

Существование куперовских пар является ключевым фактором, объясняющим феномен сверхпроводимости, при котором определенные материалы демонстрируют полное отсутствие электрического сопротивления. В обычных проводниках электроны сталкиваются с атомами кристаллической решетки, рассеиваясь и создавая сопротивление. Однако, в сверхпроводниках при низких температурах электроны объединяются в куперовские пары, связанные слабым взаимодействием, опосредованным колебаниями решетки. Эти пары ведут себя как единая квантовая сущность и могут двигаться сквозь материал без рассеяния, обеспечивая беспрепятственный поток электрического тока. $R = 0$ — таким образом, сверхпроводимость представляет собой квантово-механическое явление, открывающее возможности для создания устройств с невероятной энергоэффективностью и уникальными магнитными свойствами.

Теоретические изыскания предсказывают существование цветовой сверхпроводимости — экзотического состояния материи, возникающего при экстремальных условиях, таких как сверхвысокие энергии или плотности. В отличие от обычной сверхпроводимости, где объединяются электроны, в цветовой сверхпроводимости аналогичные пары образуют кварки — фундаментальные составляющие адронов, таких как протоны и нейтроны. Вместо электростатического притяжения, как в случае электронов, кварки связываются посредством сильного взаимодействия, опосредованного глюонами, что приводит к формированию когерентного квантового состояния. Исследование цветовой сверхпроводимости позволяет глубже понять природу сильного взаимодействия и свойства материи в самых экстремальных условиях, существующих во Вселенной, например, в ядрах нейтронных звезд или в первые моменты после Большого Взрыва.

Статистика Ферми, изначально разработанная для описания поведения электронов, оказалась фундаментальным принципом, пронизывающим исследования самых передовых состояний материи. От объяснения сверхпроводимости, где электроны объединяются в так называемые куперовские пары, до теоретических предсказаний о цветной сверхпроводимости, возникающей при экстремальных условиях с участием кварков, этот статистический подход продолжает вдохновлять ученых. Неизменная актуальность статистики Ферми демонстрирует ее мощь как инструмента для понимания коллективного поведения частиц и открывает перспективы для создания материалов с совершенно новыми свойствами, расширяя границы современной физики конденсированного состояния и стимулируя инновации в различных областях науки и техники.

Изучение статистик Ферми-Дирака, как представлено в статье, напоминает о хрупкости любых моделей. Подобно алхимику, пытающемуся удержать ртуть, физики сталкиваются с необходимостью приближения к истине через завесу неопределенности. Эрнест Резерфорд однажды заметил: «Если бы я не был бы занят, я бы посвятил себя исследованию этой проблемы». Эта фраза, несмотря на кажущуюся легкомысленность, отражает суть научного поиска — признание сложности мира и готовность к постоянным попыткам его постижения. Статья показывает, как из попыток описать поведение моноатомных газов возникло нечто, определившее облик современной физики полупроводников и астрофизики. Каждая модель — это лишь временное усмирение хаоса, и понимание этого — первый шаг к созданию следующей, чуть более совершенной иллюзии.

Куда же дальше?

История статистики Ферми-Дирака, как и любая история, — это не прямая линия, а скорее запутанный узел. Попытки реконструировать прошлое всегда лишь приближение, ведь данные — это всего лишь наблюдения в костюме истины. Нельзя забывать, что элегантность любой модели — признак её скорой гибели. Идеальные графики должны настораживать больше, чем хаотичные колебания — шум, возможно, просто правда, которой не хватило уверенности, чтобы заявить о себе.

Следующим шагом видится отказ от упрощающих предположений об идеальных газах и равновесных системах. Реальный мир, как известно, предпочитает беспорядок. Необходимо разрабатывать методы, способные описывать системы, находящиеся далеко от равновесия, где квантовые эффекты становятся доминирующими. Иначе говоря, нужно научиться предсказывать не то, что должно быть, а то, что вероятно будет.

Более того, статистику Ферми-Дирака уже давно вышли за пределы физики твердого тела и астрофизики. Её принципы проникают в самые неожиданные области — от теории информации до моделирования финансовых рынков. Возможно, самое интересное ждёт нас не в углублении в существующие теории, а в поиске принципиально новых приложений. Ведь, в конечном счете, любое уравнение — это всего лишь заклинание, которое работает до первого столкновения с реальностью.

Оригинал статьи: https://arxiv.org/pdf/2602.04484.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-06 03:09