Поверхностные плазмон-поляритоны: Квантовый взгляд на сверхсильное взаимодействие света и материи

Автор: Денис Аветисян

В статье представлена строгая квантовомеханическая модель поверхностных плазмон-поляритонов, раскрывающая механизмы сверхсильного взаимодействия света и материи в нанофотонных системах.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал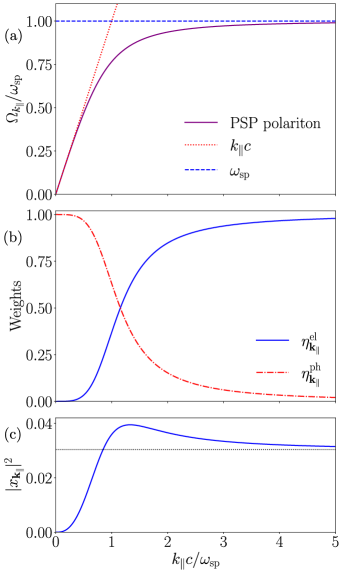

Наблюдается, что поляритонные дисперсионные соотношения <span class="katex-eq" data-katex-display="false">\Omega_{k_\parallel}</span> демонстрируют зависимость от волнового вектора <span class="katex-eq" data-katex-display="false">k_\parallel</span>, определяемую уравнением (71), при этом светлый конус <span class="katex-eq" data-katex-display="false">ck_\parallel</span> и частота поверхностных плазмонов <span class="katex-eq" data-katex-display="false">\omega_{sp}</span> формируют границы, а электронные и фотонные веса поляритонов <span class="katex-eq" data-katex-display="false">\eta_{k_\parallel}^{el}</span> и <span class="katex-eq" data-katex-display="false">\eta_{k_\parallel}^{ph}</span> модулируют их поведение, причем квадрат модуля аномального коэффициента Хопфилда <span class="katex-eq" data-katex-display="false">|x_{k_\parallel}|^2</span> в пределе <span class="katex-eq" data-katex-display="false">k_\parallel \gg \omega_p/c</span> асимптотически приближается к значению, соответствующему плазмонной популяции в основном состоянии. — Наблюдается, что поляритонные дисперсионные соотношения $\Omega_{k_\parallel}$ демонстрируют зависимость от волнового вектора $k_\parallel$ , определяемую уравнением (71), при этом светлый конус $ck_\parallel$ и частота поверхностных плазмонов $\omega_{sp}$ формируют границы, а электронные и фотонные веса поляритонов $\eta_{k_\parallel}^{el}$ и $\eta_{k_\parallel}^{ph}$ модулируют их поведение, причем квадрат модуля аномального коэффициента Хопфилда $|x_{k_\parallel}|^2$ в пределе $k_\parallel \gg \omega_p/c$ асимптотически приближается к значению, соответствующему плазмонной популяции в основном состоянии.

Исследование использует представление Пауэра-Зину-Вулли для описания поверхностных плазмон-поляритонов и демонстрирует режимы сверхсильного сцепления.

Несмотря на широкое применение, микроскопическое квантовое описание поверхностных плазмон-поляритонов до сих пор оставалось сложной задачей. В работе, озаглавленной ‘Microscopic quantum description of surface plasmon polaritons: revealing intrinsic ultrastrong light-matter coupling’, предложена новая теоретическая схема, основанная на представлении Пауэра-Зиенау-Вулли, позволяющая строго описать эти квазичастицы в произвольных металл-диэлектрических геометриях. Показано, что взаимодействие света и материи на таких границах принципиально находится в режиме сверхсильного взаимодействия, приводя к нетривиальным квантовым флуктуациям в пределе квазистатического приближения. Открывает ли это новые перспективы для управления квантовыми свойствами нанофотонных систем и создания принципиально новых устройств?

Преодолевая ограничения Друде: Необходимость квантового подхода

Классические модели, такие как модель Друде, оказываются недостаточно точными при описании взаимодействия света и материи в наномасштабе, особенно в отношении процессов диссипации энергии. Эта неспособность связана с тем, что модель Друде рассматривает электроны как классические частицы, игнорируя квантовые эффекты, которые становятся доминирующими при уменьшении размеров структур. В наноматериалах энергия света может быстро теряться из-за межэлектронных взаимодействий, локализованных поверхностных плазмонных резонансов и других квантовых явлений, которые модель Друде просто не способна адекватно учесть. Таким образом, для корректного описания и прогнозирования оптических свойств наноструктур необходим переход к более совершенным квантово-механическим подходам, учитывающим коллективное поведение электронов и сложные многочастичные взаимодействия.

Для адекватного описания коллективных электронных явлений, особенно в наноматериалах, требуется переход от полуклассических приближений к квантовой теории. В то время как классические модели, такие как модель Друде, могут дать общее представление о поведении электронов, они не способны корректно учесть квантовые эффекты, такие как туннелирование и корреляции между электронами. Многочастичные взаимодействия, возникающие из-за кулоновского отталкивания между электронами, существенно влияют на их коллективное поведение, формируя сложные квазичастицы и коллективные возбуждения, такие как плазмоны. Точное моделирование этих явлений требует решения сложных квантовомеханических задач, учитывающих влияние многих тел и корреляции, что открывает возможности для разработки новых материалов с заданными оптическими и электронными свойствами, а также для углубленного понимания фундаментальных процессов в конденсированных средах.

Точное моделирование плазмонных резонансов является ключевым фактором для прогресса в широком спектре современных технологий. Эти резонансы, возникающие при взаимодействии света с электронами в наноструктурах, лежат в основе работы высокочувствительных сенсоров, способных обнаруживать отдельные молекулы, а также перспективных метаматериалов с необычными оптическими свойствами. Понимание механизмов, определяющих форму, частоту и затухание плазмонных резонансов, позволяет целенаправленно конструировать наноструктуры с заданными характеристиками, оптимизируя их для конкретных применений — от биомедицинской диагностики и мониторинга окружающей среды до создания новых поколений оптоэлектронных устройств и солнечных батарей. Без точного моделирования, учитывающего квантовые эффекты и сложное взаимодействие множества электронов, эффективная разработка и масштабирование этих технологий становится затруднительным.

Плазмонная частота <span class="katex-eq" data-katex-display="false">\omega_\mu</span> металлодиэлектрического интерфейса связана с частотой <span class="katex-eq" data-katex-display="false">\tilde{\omega}_\mu</span> его комплементарной структуры, полученной путем обмена металлическими и диэлектрическими областями. — Плазмонная частота $\omega_\mu$ металлодиэлектрического интерфейса связана с частотой $\tilde{\omega}_\mu$ его комплементарной структуры, полученной путем обмена металлическими и диэлектрическими областями.

Представление Пауэр-Зиенау-Вулли: Квантово-механический формализм

Представление Пауэр-Зиенау-Вулли (ПЗВ) представляет собой надежный квантовомеханический формализм для анализа взаимодействия света и вещества на границах раздела сред. В основе метода лежит использование тензора Грина и разложения Гельмгольца для точного описания электромагнитных полей и их связи с электронами. ПЗВ-формализм позволяет описывать как когерентные, так и некогерентные взаимодействия, включая эффекты, обусловленные локальной плотностью состояний, и обеспечивает возможность расчета оптических свойств материалов, находящихся вблизи поверхностей и наноструктур. В отличие от некоторых других подходов, ПЗВ-формализм не ограничивается слабыми возмущениями и может применяться для исследования сильно связанных режимов, что особенно важно при изучении плазмонных явлений и метаматериалов.

Метод PZW для описания электромагнитных полей и их взаимодействия с электронами опирается на ряд математических инструментов. Ключевым является использование тензора Грина $G(\mathbf{r}, \mathbf{r}')$ , позволяющего найти решение уравнения Гельмгольца для заданного источника. Разложение Гельмгольца позволяет разделить векторное поле на составляющие с нулевым и ненулевым ротором, упрощая анализ. Решения уравнения Лапласа $\nabla^2 \phi = 0$ применяются для определения скалярного потенциала, необходимого для расчета электростатического поля, а также для описания поведения электромагнитных волн в различных средах. Комбинация этих элементов позволяет получить точное и полное описание электромагнитных полей на границах раздела сред и их взаимодействие с электронами в материале.

Использование представления Пауэр-Зиенау-Вулли (ПЗВ) позволяет выйти за рамки возмущающих методов расчета и исследовать сильносвязанные режимы взаимодействия света и вещества. В отличие от подходов, основанных на малой интенсивности возбуждения, ПЗВ-формализм не вводит ограничений на амплитуду электромагнитного поля, что делает его применимым для описания нелинейных оптических явлений и процессов, протекающих вблизи металлических наноструктур. Это открывает возможности для детального изучения и контроля плазмонных резонансов, а также для разработки новых устройств, основанных на управлении световыми полями на наноуровне, например, сенсоров и оптических переключателей. $\vec{E}(\vec{r}, \omega)$ и $\vec{J}(\vec{r}, \omega)$ могут быть рассчитаны самосогласованно, учитывая взаимное влияние электрического поля и индуцированного тока.

Сферическая металлическая наночастица радиуса <i>a</i> с диэлектрической функцией <span class="katex-eq" data-katex-display="false">\varepsilon_1(\omega)=\varepsilon_\in fty-\omega^2_p/\omega^2</span> в диэлектрической среде характеризуется продольной (синие линии) и поперечной (пунктир красного цвета) поляризацией для основного локализованного плазмонного режима (l=1), при этом поляризационные линии перпендикулярного поля замыкаются в кольца, а параллельного - простираются от отрицательных к положительным зарядам. — Сферическая металлическая наночастица радиуса a с диэлектрической функцией $\varepsilon_1(\omega)=\varepsilon_\in fty-\omega^2_p/\omega^2$ в диэлектрической среде характеризуется продольной (синие линии) и поперечной (пунктир красного цвета) поляризацией для основного локализованного плазмонного режима (l=1), при этом поляризационные линии перпендикулярного поля замыкаются в кольца, а параллельного — простираются от отрицательных к положительным зарядам.

Поверхностные плазмон-поляритоны: коллективные возбуждения

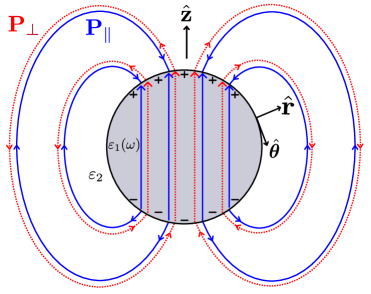
Поверхностные плазмон-поляритоны (ППП) представляют собой гибридные возбуждения, возникающие вследствие сильного взаимодействия света с коллективными колебаниями электронов на границе раздела металл-диэлектрик. Этот процесс обусловлен когерентным возбуждением свободных электронов в металле электромагнитным полем света, что приводит к образованию квазичастиц — поляритонов. Взаимодействие характеризуется передачей энергии и импульса между фотоном и плазмоном, что изменяет как частоту, так и длину волны распространения возбуждения. $\omega_{SPP} = \sqrt{\frac{\omega_p^2}{\epsilon_d + \epsilon_m}}$ , где $\omega_{SPP}$ — частота ППП, $\omega_p$ — плазменная частота металла, а $\epsilon_d$ и $\epsilon_m$ — диэлектрические проницаемости диэлектрика и металла соответственно. Интенсивность и характеристики ППП существенно зависят от свойств материалов, геометрии интерфейса и длины волны света.

Представление ПЗВ обеспечивает удобный способ описания как локализованных, так и распространяющихся поверхностных плазмон-поляритонов (ППП). В рамках этого подхода, ППП рассматриваются как суперпозиция электромагнитных волн и колебаний электронной плотности на границе раздела металл-диэлектрик. Математически, дисперсионное соотношение для ППП, выраженное через волновой вектор $k$ и частоту ω, определяет их поведение и свойства, позволяя рассчитывать такие параметры, как длина затухания и эффективная масса. Использование представления ПЗВ позволяет последовательно описывать различные типы ППП, включая волны, распространяющиеся вдоль плоской поверхности, и локализованные плазмонные резонансы в наноструктурах, предоставляя полную картину их физических характеристик и возможностей применения.

Понимание дисперсионного соотношения и длины затухания поверхностных плазмон-поляритонов (ППП) является ключевым для проектирования и оптимизации плазмонных устройств. Дисперсионное соотношение $\omega(k)$ , связывающее частоту ω и волновой вектор $k$ , определяет характеристики распространения ППП и возможность достижения эффектов замедления и усиления света. Длина затухания, обусловленная потерями в металле и диэлектрике, ограничивает расстояние, на котором ППП могут эффективно распространяться и взаимодействовать со светом. Контроль над этими параметрами позволяет создавать нанооптические устройства, такие как сенсоры, метаматериалы и устройства для обработки информации, работающие в масштабах, меньших длины волны света, что невозможно с использованием традиционной оптики.

Зависимость популяции плазмонов в объеме от порядка моды для металлической сферы (красные точки) и ее комплементарной сферической полости (синие квадраты) при <span class="katex-eq" data-katex-display="false">\epsilon_2 = 1</span> и <span class="katex-eq" data-katex-display="false">\epsilon_\in fty = 1</span> демонстрирует сходимость к асимптотическому пределу плоской поверхности (пунктирная линия). — Зависимость популяции плазмонов в объеме от порядка моды для металлической сферы (красные точки) и ее комплементарной сферической полости (синие квадраты) при $\epsilon_2 = 1$ и $\epsilon_\in fty = 1$ демонстрирует сходимость к асимптотическому пределу плоской поверхности (пунктирная линия).

Ультрасильное взаимодействие и поляритоны: новые горизонты

Когда сила взаимодействия света и материи превышает собственные энергетические уровни системы, возникает режим ультрасильного взаимодействия. В этом режиме традиционное разделение между светом и материей стирается, и они начинают функционировать как единое гибридное образование. Это не просто усиление взаимодействия, а фундаментальное изменение характера энергии в системе, где энергия взаимодействия становится сопоставимой или даже превышает внутренние энергии рассматриваемого материала. В результате, энергетические уровни системы претерпевают значительные модификации, проявляющиеся в новых спектральных характеристиках и формировании качественно новых квазичастиц, отличных от как чисто световых, так и чисто материальных возбуждений. Такой режим открывает возможности для управления светом и материей на беспрецедентном уровне и лежит в основе перспективных технологий в области квантовой оптики и материаловедения.

В условиях сильного взаимодействия света и материи возникают квазичастицы — поляритоны, представляющие собой гибридные состояния, сочетающие в себе свойства фотона и возбуждения материала. Эти новые образования демонстрируют существенные изменения в своих спектральных характеристиках по сравнению с исходными компонентами, что проявляется в смещении частот, появлении новых резонансов и перераспределении осцилляторной силы. Поляритоны не являются просто суперпозицией света и материи, а представляют собой качественно новые объекты с уникальными свойствами, открывающими возможности для создания принципиально новых оптических и электронных устройств.

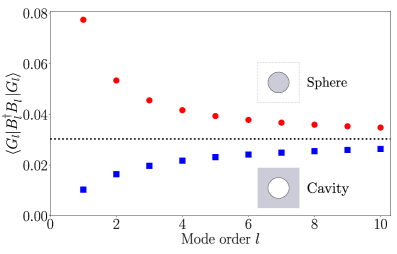
Разделение Раби, являющееся характерным признаком сильного взаимодействия света и материи, служит прямым индикатором интенсивности этого взаимодействия и подтверждает формирование поляритонных состояний. Моделирование показывает, что плазмонно-фотонные системы функционируют в режиме ультрасильного взаимодействия, что проявляется в наличии конечной популяции плазмонов в основном состоянии, составляющей примерно 0.03. Этот результат указывает на принципиальную возможность создания устройств, основанных на когерентном контроле плазмонными возбуждениями, и открывает перспективы для разработки новых оптических и квантовых технологий, использующих уникальные свойства поляритонов, сформированных в таких системах.

Металл-диэлектрический интерфейс состоит из металлической области с пренебрежимо малыми нерадиационными потерями, описываемой диэлектрической проницаемостью типа Друде <span class="katex-eq" data-katex-display="false">\varepsilon_1(\omega)=\varepsilon_\in fty - \omega_p^2/\omega^2</span>, и прилегающей диэлектрической области с положительной диэлектрической проницаемостью <span class="katex-eq" data-katex-display="false">\varepsilon_2 > 0</span>, при этом единичный вектор <span class="katex-eq" data-katex-display="false">\mathbf{N}</span> ориентирован перпендикулярно границе раздела и направлен в диэлектрическую среду. — Металл-диэлектрический интерфейс состоит из металлической области с пренебрежимо малыми нерадиационными потерями, описываемой диэлектрической проницаемостью типа Друде $\varepsilon_1(\omega)=\varepsilon_\in fty - \omega_p^2/\omega^2$ , и прилегающей диэлектрической области с положительной диэлектрической проницаемостью $\varepsilon_2 > 0$ , при этом единичный вектор $\mathbf{N}$ ориентирован перпендикулярно границе раздела и направлен в диэлектрическую среду.

Потери энергии и их влияние на плазмонные системы: вызовы и перспективы

Энергопотери, возникающие вследствие омического сопротивления и излучательной затухания, оказывают решающее влияние на эффективность плазмонных устройств. Омические потери, обусловленные рассеянием электронов на дефектах кристаллической решетки и фононах, приводят к нагреву материала и снижению интенсивности плазмонного сигнала. Радиационное затухание, напротив, связано с излучением энергии в окружающую среду, что также уменьшает продолжительность жизни плазмонных колебаний. Величина этих потерь напрямую коррелирует с размером и формой наноструктур, материалом и длиной волны возбуждения. В результате, понимание и минимизация этих процессов является критически важной задачей для создания высокопроизводительных плазмонных сенсоров, солнечных элементов и других перспективных устройств. Моделирование показывает, что плотность объемных плазмонов составляет 3.0×10^-2, что приводит к сдвигу частоты $ω<sub>p</sub>$ .

Понимание природы и величины потерь энергии в плазмонных системах является ключевым фактором для оптимизации конструкции устройств и повышения их эффективности. Эти потери, возникающие из-за омического сопротивления и излучения, существенно ограничивают время жизни плазмонных возбуждений и, как следствие, производительность устройств. Тщательный анализ этих механизмов потерь позволяет целенаправленно модифицировать материалы и геометрию устройств, минимизируя диссипацию энергии и максимизируя полезный сигнал. Например, исследование показывает, что величина потерь напрямую связана с частотой плазмонного резонанса $ω_p$ и концентрацией электронов, что позволяет точно прогнозировать и контролировать характеристики устройств. Оптимизация на основе понимания этих потерь открывает возможности для создания более чувствительных сенсоров, эффективных систем сбора энергии и перспективных квантовых технологий.

Перспективные исследования в области плазмоники направлены на разработку эффективных стратегий минимизации потерь энергии и увеличения времени жизни плазмонных возбуждений. Моделирование показывает, что при определенной конфигурации удается достичь плотности плазмонной популяции в 3.0×10^-2, сопровождающейся сдвигом частоты $ω<sub>p</sub>$ . Такие достижения открывают возможности для создания высокочувствительных сенсоров, эффективных систем сбора энергии и перспективных квантовых технологий, где ключевым фактором является длительное сохранение когерентности плазмонных состояний и минимизация диссипации энергии. Повышение стабильности и продолжительности жизни плазмонов позволит значительно улучшить характеристики устройств и расширить область их применения.

Без точного определения задачи любое решение — шум. Данное исследование демонстрирует необходимость строгой математической формулировки для описания поверхностных плазмон-поляритонов. Авторы, используя представление Пауэра-Зиенау-Вулли, вышли за рамки классических моделей, предложив rigorозное квантовомеханическое описание. Это позволило выявить режимы ультрасильного взаимодействия света и вещества, что принципиально важно для понимания нанофотонных систем. Как однажды заметил Макс Планк: «Всё, что мы знаем, — это капля в море всего того, что мы не знаем.» В данном случае, работа представляет собой попытку расширить границы этой «капли» в области взаимодействия света и материи, предоставляя математически доказуемый фундамент для дальнейших исследований в области нанофотоники.

Что дальше?

Представленный анализ, хоть и опирается на строгое математическое описание поверхностных плазмон-поляритонов посредством представления Пауэра-Зиенау-Вулли, не снимает всех вопросов. Доказательство существования ультрасильного взаимодействия — это лишь первый шаг. Следующим, неизбежно, станет необходимость разработки методов контроля над этим взаимодействием, а не просто его констатации. Нынешние подходы, опирающиеся на численные методы, хоть и дают полезные результаты, не обладают той элегантностью, которая присуща строгому математическому аппарату.

Особое внимание следует уделить влиянию дисперсии на наблюдаемые эффекты. Приближение квазистатического режима, хоть и упрощает задачу, не может считаться универсальным. В реальности, конечно, дисперсионные эффекты вносят существенную коррекцию, и пренебрежение ими — это, скорее, удобство для исследователя, чем физическая истина. Необходимо развитие аналитических методов, позволяющих учитывать дисперсию без потери математической строгости.

В конечном счете, истинный прогресс заключается не в увеличении числа публикаций, а в создании предсказательной теории. Теории, которая не просто описывает наблюдаемые явления, но и предсказывает новые, позволяя создавать материалы и устройства с заранее заданными свойствами. И лишь тогда можно будет говорить о реальном контроле над светом и материей.

Оригинал статьи: https://arxiv.org/pdf/2601.11297.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-19 19:28