Автор: Денис Аветисян
В статье представлен метод функциональной ренормализационной группы для изучения коррелированных фаз, возникающих на поверхности и границах слоистых квантовых материалов.
Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.
Бесплатный телеграм-канал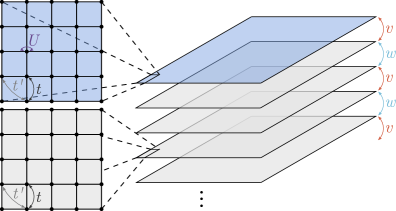
Разработано поверхностное приближение функциональной ренормализационной группы для трехмерной модели Хаббарда-СШ, позволяющее исследовать влияние поверхности на формирование спин-волновых и сверхпроводящих состояний.
Поверхностные состояния в слоистых квантовых материалах часто остаются за пределами возможностей стандартных методов теоретического анализа. В работе ‘Surface Functional Renormalization Group for Layered Quantum Materials’ предложен новый подход, расширяющий функциональную ренормализационную группу для эффективного изучения взаимодействий на поверхности и границах трехмерных систем. Показано, что применение метода к модели Хаббарда-SSH позволяет отследить эволюцию коррелированных состояний и выявить возможность возникновения хирального спинового связного порядка. Какие новые фазы и топологические свойства могут быть обнаружены в слоистых материалах с помощью этого метода?
Поверхностные Взаимодействия и Модель Хаббарда-Шульца-Саттера
Понимание систем с сильными электронными взаимодействиями имеет первостепенное значение для материаловедения, однако традиционные теоретические модели зачастую оказываются недостаточными при описании поверхностных эффектов. Это связано с тем, что на поверхности нарушается симметрия кристаллической решетки, и электронные состояния становятся более локализованными, что усиливает роль электронных корреляций. В то время как объемные материалы можно адекватно описать с использованием упрощенных подходов, учет влияния пониженной размерности и специфических поверхностных состояний требует более сложных моделей, способных точно воспроизводить наблюдаемые физические свойства. Игнорирование этих факторов приводит к неверному предсказанию критических температур, магнитных свойств и других ключевых характеристик материалов, что существенно затрудняет разработку новых материалов с заданными свойствами.
Модель Хаббарда-Шульца-Саттера (Hubbard-SSH) представляет собой мощный теоретический инструмент, позволяющий исследовать взаимодействие между коррелированными электронами и пониженной размерностью поверхностных систем. В отличие от традиционных моделей, которые часто упрощают описание электронных взаимодействий, эта модель учитывает как кулоновское отталкивание между электронами (U), так и особенности их перемещения по цепи, включая переходы между ближайшими и следующими ближайшими атомами. Это особенно важно для анализа свойств поверхностей и наноструктур, где эффекты размерности и корреляций становятся доминирующими. Способность модели адекватно описывать эти явления открывает возможности для предсказания и понимания экзотических электронных фаз и свойств материалов, которые могут быть использованы в новых технологиях.
В рамках модели Хаббарда-SSH ключевую роль играет учет параметров, определяющих поведение системы на поверхности. В частности, включение параметра перескока на ближайшие соседи и химического потенциала позволяет точно описывать влияние поверхностной размерности и электронных взаимодействий. Перескок на ближайшие соседи влияет на подвижность электронов и формирование полосовой структуры, тогда как химический потенциал определяет заполнение электронных уровней и, следовательно, электронные свойства материала. Комбинируя эти параметры с взаимодействием Хаббарда U, можно тонко настраивать электронный ландшафт и исследовать возможность возникновения экзотических фаз, таких как сверхпроводящие или магнитные состояния, отличающиеся от объемных аналогов. Влияние этих параметров проявляется в изменении плотности состояний и спектральных функций, что критически важно для понимания наблюдаемых экспериментальных данных.
Электронная структура и фазовые переходы в системах с сильными корреляциями существенно зависят от взаимодействия между электронами, описываемого параметром Хаббарда U, а также от особенностей топологии и размерности материала. Проведенные вычисления в рамках модели Хаббарда-SSH исследуют влияние различных значений U, конкретно 3 и 5, на формирование электронной структуры и возможность возникновения экзотических фаз. Изменение параметра U влияет на баланс между кинетической энергией электронов и энергией кулоновского отталкивания, что приводит к перестройке электронной плотности и возникновению новых состояний. Результаты демонстрируют, что при определенных значениях U и при наличии поверхностных эффектов, система может проявлять нетривиальные фазы, характеризующиеся, например, топологической защищенностью или спиновыми неупорядоченностями.
Функциональная Ренормализационная Группа для Поверхностных Систем
Функциональная ренормализационная группа (ФРГ) представляет собой мощный непертурбативный метод исследования многочастичных систем, однако применение ФРГ к поверхностям сопряжено с рядом специфических трудностей. В отличие от объемных систем, поверхности характеризуются пониженной размерностью и наличием граничных условий, которые необходимо явно учитывать в ренормализационном потоке. Это требует модификации стандартных процедур ФРГ, в частности, корректного учета граничных условий при интегрировании по высокоэнергетическим степеням свободы. Кроме того, поверхностные взаимодействия и эффекты корреляции могут существенно отличаться от объемных, что требует разработки специальных схем регуляризации и соответствующих функциональных интегралов для корректного описания физики поверхности. Игнорирование этих факторов может привести к неверным результатам и искаженному пониманию свойств поверхностных систем.
Поверхностный FRG (функциональная ренормализационная группа) является расширением стандартного FRG, адаптированным для описания систем с поверхностями. В отличие от объемных систем, поверхности характеризуются пониженной размерностью и специфическими граничными условиями, которые существенно влияют на поведение многих тел. В поверхностном FRG эти факторы учитываются явно при выводе ренормализационного потока. Это достигается путем модификации функционала действия и использования граничных условий, соответствующих конкретной поверхности. Такой подход позволяет корректно описывать электронные состояния, взаимодействия и фазовые переходы, возникающие на поверхности, что невозможно в рамках стандартного FRG, предназначенного для объемных материалов.
Метод функциональной ренормализационной группы (FRG) позволяет проводить систематический анализ взаимодействий и корреляционных эффектов в поверхностных системах, выявляя слабые тенденции к упорядочению, которые могут быть упущены при использовании более простых методов. В отличие от приближений, основанных на усреднении, FRG не требует априорного знания о структуре основного состояния и позволяет отслеживать эволюцию взаимодействий с изменением энергетической шкалы. Это особенно важно для систем с сильными корреляциями, где стандартные методы теории возмущений неприменимы. FRG обеспечивает возможность учета флуктуаций и динамических эффектов, что приводит к более точному описанию фазовых переходов и критического поведения на поверхности.
В рамках метода функциональной ренормализационной группы (FRG) для поверхностных систем, ренормализация взаимодействий осуществляется итеративным исключением высокоэнергетических степеней свободы. Этот процесс предполагает последовательное «интегрирование» по колебаниям с высокой энергией, что приводит к эффективному изменению взаимодействий между оставшимися степенями свободы с низкой энергией. В результате формируется уравнение потока \frac{\partial}{\partial \Lambda} \Gamma_k, описывающее эволюцию эффективного действия \Gamma_k в зависимости от масштаба энергии Λ. Данное уравнение позволяет проследить изменение взаимодействий с изменением энергетического масштаба и, следовательно, определить стабильные фазы и критические явления в системе.
Раскрытие Спин-Плотнистной Волновой Упорядоченности
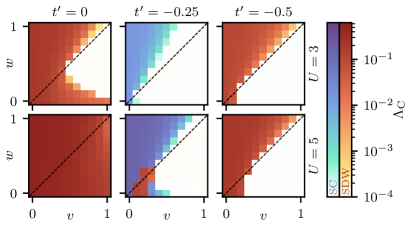
Расчеты в рамках поверхностной функциональной ренормализационной группы (Surface FRG) предсказывают возникновение спин-плотностной волны (SDW) в модели Хаббарда-Шульца-Саттера при определенных условиях. Данное явление наблюдается в зависимости от параметров модели, включая силу взаимодействия и параметры перескоков. В частности, установлено, что SDW порядок формируется как результат конкуренции между кинетической энергией электронов и кулоновским отталкиванием, что приводит к пространственной модуляции спиновых степеней свободы. Важно отметить, что условия возникновения SDW зависят от конкретных значений параметров модели, и их точное определение требует детального анализа результатов численных расчетов.
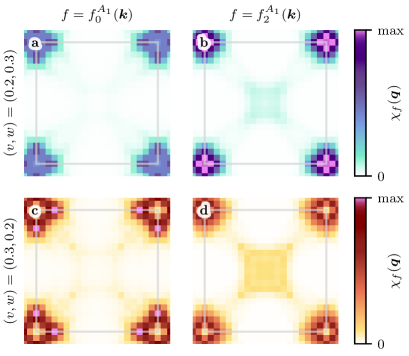
Наши расчеты демонстрируют возникновение инкомменсуратного спин-плотностного волнового порядка (SDW), характеризующегося длиной волны, не соответствующей периоду кристаллической решетки. Инкомменсуратность означает, что период SDW-модуляции не является рациональным кратным периоду решетки, что приводит к более сложной структуре спиновых упорядочений. В отличие от комменсуратных SDW, где спиновая структура повторяется через фиксированное количество элементарных ячеек, инкомменсуратные SDW характеризуются непериодичностью и требуют более детального анализа для определения их пространственной конфигурации и энергетических свойств. В наших моделях, величина длины волны инкомменсуратного SDW определяется параметрами взаимодействия и кинетическими свойствами системы.
Форм-фактор и хиральная суперпозиция играют ключевую роль в стабилизации инкомменсуратной фазы спин-плотностных волн (SDW). Анализ показывает, что эти параметры определяют пространственную модуляцию спиновой структуры, влияя на длину волны и ориентацию спинов. В частности, вклад хиральной суперпозиции приводит к возникновению спиральной спиновой текстуры, в то время как специфический вид форм-фактора определяет предпочтительные волновые векторы для инкомменсуратного SDW-порядка. Изменение этих параметров приводит к модификации спиновой текстуры и, как следствие, к изменению физических свойств системы.
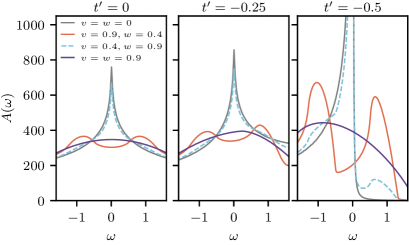
Анализ спектральной функции подтверждает наличие спин-волнового порядка (SDW). В спектре наблюдаются характерные особенности, соответствующие образованию SDW. Критический масштаб \Lambda_C, определяющий стабильность SDW-фазы, демонстрирует зависимость от параметров перескока v и w, а также от силы взаимодействия. Изменение этих параметров приводит к смещению критического масштаба, что влияет на температуру и другие условия возникновения SDW-упорядоченного состояния. Данная зависимость позволяет контролировать и настраивать свойства SDW-фазы путем варьирования параметров системы.
Влияние и Перспективы Дальнейших Исследований
Предсказанный неколлективный спин-плотностной волновой порядок (SDW) имеет существенное значение для понимания магнитных свойств поверхностей и тонких пленок. Неколлективный характер SDW, в отличие от коллективных магнитных состояний, обуславливает уникальные магнитные характеристики, проявляющиеся в тонких структурах. Теоретические расчеты показывают, что в подобных системах магнитные моменты располагаются не параллельно друг другу, а образуют сложную, непериодическую структуру, что влияет на магнитооптические свойства и взаимодействие с внешними магнитными полями. Данное явление особенно актуально для разработки новых материалов с управляемыми магнитными характеристиками, востребованных в современной спинтронике и технологиях хранения данных, где контроль над спиновыми степенями свободы играет ключевую роль.
Представленная работа закладывает теоретическую основу для конструирования материалов с заданными магнитными свойствами, что открывает перспективы для развития спинтроники. Исследование демонстрирует возможность целенаправленного управления магнитным упорядочением на поверхности материалов посредством изменения параметров системы, таких как параметры перескока v и w. Эта возможность позволяет создавать материалы с улучшенными характеристиками для спинтронных устройств, например, для магнитной памяти и логических схем. Разработанный теоретический подход позволяет предсказывать и оптимизировать магнитные свойства новых материалов, предоставляя ценный инструмент для материаловедения и нанотехнологий, и, в конечном итоге, способствуя созданию более эффективных и компактных электронных устройств.
Перспективные исследования направлены на изучение взаимосвязи между спин-плотностной волной (SDW) и сверхпроводимостью в аналогичных системах. Установление природы этого взаимодействия может привести к открытию новых механизмов сверхпроводимости, отличных от традиционных, основанных на электрон-фононном взаимодействии. Предполагается, что SDW-упорядочение может играть роль в опосредовании спаривания куперовских пар, что особенно актуально для нетрадиционных сверхпроводников. Изучение этих взаимосвязей требует комплексного подхода, сочетающего теоретическое моделирование и экспериментальные исследования, направленные на выявление условий, при которых SDW и сверхпроводимость могут сосуществовать или даже усиливать друг друга, открывая путь к созданию материалов с улучшенными сверхпроводящими свойствами и потенциальными приложениями в различных областях науки и техники.
Дальнейшее развитие метода функционального ренормализационной группы на поверхности (Surface FRG) с включением дополнительных взаимодействующих степеней свободы представляется перспективным направлением исследований. Систематическое варьирование параметров перескока — v и w — в диапазоне от 0 до 1 позволило детально изучить влияние этих параметров на фазовую диаграмму системы. Ожидается, что учет дополнительных взаимодействий не только расширит понимание существующих фаз, но и предскажет возникновение новых, более сложных и интересных магнитных структур. Такой подход открывает возможности для создания материалов с заданными магнитными свойствами и потенциальным применением в спинтронике, а также для исследования взаимосвязи между различными типами магнитных упорядочений и другими физическими явлениями, такими как сверхпроводимость.
Исследование, представленное в данной работе, демонстрирует важность понимания взаимодействия на поверхности и в объеме материала для возникновения коррелированных фаз. Авторы, применяя метод функциональной ренормализационной группы к трехмерной модели Хаббарда-ШШ, акцентируют внимание на эволюции структуры и ее влиянии на свойства системы. Это напоминает о мудрости Марка Аврелия: «Всё, что происходит с тобой, — это внешнее; в твоей власти только то, как ты это воспринимаешь». Подобно тому, как внешние воздействия формируют наше восприятие, так и поверхностные состояния определяют поведение всей системы, влияя на возникновение таких явлений, как спин-волновые состояния или сверхпроводимость. Структура, тщательно изученная авторами, действительно определяет поведение материала, что соответствует принципам элегантного дизайна и системного мышления.
Куда дальше?
Представленная работа, исследуя коррелированные фазы на поверхностях и границах раздела с помощью поверхностной функциональной ренормализационной группы, неизбежно ставит вопрос: что именно оптимизируется в столь сложных системах? Упор на модель Хаббарда-SSH, хотя и позволяет пролить свет на ключевые аспекты, всё же является упрощением. Истинные материалы обладают куда более богатой структурой, и влияние различных типов поверхностей, дефектов и внешних воздействий остаётся областью для дальнейших исследований. Простота модели, хоть и необходима для аналитической ясности, не должна заслонять необходимость учёта дополнительных степеней свободы.
Очевидным шагом представляется расширение метода на более сложные модели, включающие, например, кулоновское взаимодействие дальнего радиуса действия. Кроме того, важным представляется разработка эффективных численных методов, позволяющих исследовать поведение системы в широком диапазоне параметров. Поиск универсальных закономерностей, связывающих поверхностные состояния с объёмными фазами, остаётся сложной, но плодотворной задачей. Следует помнить, что хорошая система — живой организм, и вмешательство в одну её часть требует понимания функционирования целого.
В конечном итоге, настоящая работа лишь подчёркивает глубокую взаимосвязь между структурой и поведением. Оптимизация не должна сводиться к максимизации определённой величины, но к достижению элегантного баланса между различными взаимодействиями. Истинное понимание коррелированных электронных систем требует не только математической строгости, но и философского осмысления лежащих в их основе принципов.
Оригинал статьи: https://arxiv.org/pdf/2601.11055.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Все рецепты культистского круга в Escape from Tarkov
- Решение головоломки с паролем Absolum в Yeldrim.
- Лучшие транспортные средства в Far Cry 6
- Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip
- Репозиторий: Как исправить таймаут клиента
- Кто такая Кселия Мендес-Джонс? 5 вещей, которые нужно знать об актере Fallout
- Как получить скины Alloyed Collective в Risk of Rain 2
- В стороне: QB и я В ролях: каждый актер, который появляется (фотографии)
- Jujutsu Kaisen Modulo Глава 18: Предварительный просмотр: Полная мощь Рики и Цуруги.
- Лучшие шаблоны дивизий в Hearts Of Iron 4
2026-01-20 03:38