Предел чёрной дыры: нарушен ли третий закон?

Автор: Денис Аветисян

Новое исследование показывает, что в вакуумной гравитации возможно формирование экстремальных чёрных дыр, что ставит под сомнение один из фундаментальных принципов чёрной дыры.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал

При решении типа (i) с <span class="katex-eq" data-katex-display="false">A_k = 2k = 2g</span> наблюдается, что при <span class="katex-eq" data-katex-display="false">V = 0</span> величина <span class="katex-eq" data-katex-display="false">J</span> стремится к нулю, однако <span class="katex-eq" data-katex-display="false">m_H</span> остается положительной, что указывает на специфическое поведение параметров Φ и <span class="katex-eq" data-katex-display="false">\mathcal{B}</span> при приближении к пределу EMP. — При решении типа (i) с $A_k = 2k = 2g$ наблюдается, что при $V = 0$ величина $J$ стремится к нулю, однако $m_H$ остается положительной, что указывает на специфическое поведение параметров Φ и $\mathcal{B}$ при приближении к пределу EMP.

Работа демонстрирует нарушение третьего закона чёрной дыры при рассмотрении коллапса в пятимерном пространстве-времени, используя численные методы и анализ решений Myers-Perry.

Традиционное представление о третьем законе термодинамики черных дыр, утверждающее невозможность достижения экстремального состояния за конечное время, долгое время считалось непреложным. В работе «Нарушение третьего закона механики черных дыр в вакуумной гравитации» представлены численные решения, демонстрирующие формирование экстремальных вращающихся черных дыр из схватившейся гравитацией материи в пятимерном пространстве-времени. Полученные результаты впервые свидетельствуют о нарушении третьего закона в чистой вакуумной гравитации, независимо от наличия материи, и ставят под вопрос фундаментальные принципы черной дыры. Какие новые горизонты открывает это открытие для понимания динамики черных дыр и эволюции Вселенной?

Чёрные дыры: Основы Вселенной и Законы Физики

Общая теория относительности, разработанная Альбертом Эйнштейном, представляет собой краеугольный камень современного понимания гравитации и структуры пространства-времени. Эта теория описывает гравитацию не как силу, а как искривление пространства-времени, вызванное массой и энергией. Именно в рамках этой теории возникла возможность предсказать существование чёрных дыр — областей пространства-времени, где гравитация настолько сильна, что ничто, даже свет, не может их покинуть. Математический аппарат общей теории относительности позволяет точно описывать поведение материи вблизи чёрных дыр, предсказывать их свойства, такие как масса, заряд и угловой момент, и исследовать влияние этих объектов на окружающее пространство-время. $R_{\mu\nu} - \frac{1}{2}g_{\mu\nu}R + \Lambda g_{\mu\nu} = \frac{8\pi G}{c^4}T_{\mu\nu}$ — это ключевое уравнение, описывающее взаимосвязь между геометрией пространства-времени и распределением материи и энергии, которое является основой для всех расчетов, связанных с чёрными дырами.

Механика чёрных дыр представляет собой удивительную параллель с классической термодинамикой, устанавливая набор законов, управляющих поведением этих экзотических объектов. Вместо температуры и энтропии, чёрные дыры характеризуются поверхностной гравитацией и площадью горизонта событий. Первый закон связывает изменение массы чёрной дыры с изменениями её углового момента и электрического заряда, аналогично первому закону термодинамики, связывающему изменение внутренней энергии с теплом и работой. Второй закон гласит, что площадь горизонта событий чёрной дыры никогда не уменьшается, что напоминает второй закон термодинамики о возрастании энтропии. Эти аналогии не просто математические совпадения; они указывают на глубокую связь между гравитацией, термодинамикой и, возможно, квантовой гравитацией, предлагая интригующие перспективы для понимания фундаментальной природы Вселенной. $A = 4\pi r^2$

Третий закон чёрных дыр представляет собой фундаментальное ограничение, определяющее эволюцию этих экзотических объектов. В отличие от классической термодинамики, где абсолютный ноль недостижим, чёрные дыры не могут полностью «охладиться» и достичь состояния нулевой температуры за конечное время. Этот закон гласит, что невозможно полностью остановить уменьшение площади горизонта событий чёрной дыры за конечное время, что накладывает ограничения на процессы, происходящие вблизи и внутри чёрной дыры. $dA/dt \ge 0$ , где $A$ — площадь горизонта событий, а $t$ — время, демонстрирует, что площадь может только увеличиваться или оставаться постоянной, но не уменьшаться. Данное ограничение тесно связано с энтропией чёрной дыры и указывает на глубокую связь между гравитацией, термодинамикой и информацией, что делает Третий закон ключевым элементом в понимании фундаментальной природы Вселенной.

Изучение законов, управляющих чёрными дырами, представляет собой не просто астрофизическую задачу, но и фундаментальный способ проверки пределов современной физики. Эти законы, особенно третий закон чёрных дыр, накладывают ограничения на эволюцию этих объектов и позволяют исследователям углубляться в природу пространства-времени. Анализ этих ограничений может выявить несоответствия между общей теорией относительности и квантовой механикой, открывая путь к созданию более полной теории гравитации. Понимание этих закономерностей позволяет выдвигать гипотезы о сингулярностях, горизонте событий и, возможно, даже о структуре Вселенной за пределами наблюдаемого космоса. Исследование чёрных дыр, таким образом, является уникальным инструментом для изучения самых фундаментальных аспектов реальности и поиска ответов на вопросы о природе пространства, времени и гравитации.

Нарушение Третьего Закона: Влияние Материи

Третий закон термодинамики, утверждающий невозможность достижения абсолютного нуля в конечном числе шагов, не является универсальным. Определенные модели материи, в частности, так называемая “тонкослойная материя” (Thin Shell Matter), демонстрируют возможность нарушения этого закона. В таких моделях, характеризующихся специфической структурой и распределением массы, черные дыры могут приближаться к экстремальному состоянию (с нулевым электрическим зарядом и угловым моментом) без необходимости бесконечного снижения энтропии, что противоречит классической формулировке Третьего закона. Это связано с тем, что тонкослойная материя изменяет геометрию пространства-времени вблизи горизонта событий, облегчая процесс достижения экстремального состояния.

Первоначальные рассуждения о возможности нарушения третьего закона термодинамики основывались на модели ‘гладкого вещества’ (smooth matter), предполагающей высокую дифференцируемость метрики. Однако, аргумент Келе-Унгера (Kehle-Unger argument) показал, что даже вещество с неограниченной дифференцируемостью может быть сконфигурировано таким образом, чтобы обойти ограничения, накладываемые третьим законом. В частности, было продемонстрировано, что при определенных условиях, конфигурация материи может позволить чёрной дыре приближаться к экстремальному состоянию, не нарушая при этом локальные законы физики, но тем самым ставя под сомнение универсальность третьего закона.

Вопрос о том, что препятствует достижению чёрной дырой экстремального состояния, является фундаментальным в контексте нарушения Третьего закона термодинамики. Экстремальная чёрная дыра характеризуется нулевой температурой и, следовательно, потенциальной способностью накапливать бесконечное количество энергии без увеличения энтропии. Теоретически, это противоречит Третьему закону, который утверждает, что энтропия системы должна стремиться к конечному значению при приближении температуры к абсолютному нулю. Существующие модели материи, такие как тонкослойная материя, демонстрируют возможность обхода этого закона, указывая на то, что конфигурация материи вокруг чёрной дыры играет ключевую роль в определении её способности достичь экстремального состояния. Понимание механизмов, предотвращающих достижение этого состояния, требует более глубокого исследования взаимодействия между гравитацией, термодинамикой и свойствами материи в экстремальных условиях.

Изучение взаимодействия между конфигурацией материи и третьим законом термодинамики требует углубленного исследования, поскольку существующие модели, такие как «тонкослойная материя» и даже высокодифференцируемая материя, демонстрируют возможность нарушения закона. Это указывает на то, что стандартные предположения о гладкости материи недостаточны для однозначного подтверждения третьего закона в экстремальных гравитационных условиях. Дальнейшие исследования направлены на установление точных критериев, определяющих, при каких конфигурациях материи возможно приближение к экстремальному состоянию черной дыры, и выявление фундаментальных ограничений, препятствующих полному нарушению третьего закона. Такой подход расширяет границы теоретического понимания и требует разработки новых математических инструментов и физических моделей.

Численное Моделирование: Конструирование Решений в Пространстве-Времени

Численные методы представляют собой необходимый инструмент для построения и анализа сложных пространств-времен вокруг черных дыр, когда аналитические решения становятся невозможными или слишком сложными для вычислений. В отличие от подходов, основанных на точных математических формулах, численные методы аппроксимируют решения дифференциальных уравнений, описывающих гравитационное поле, используя дискретизацию пространства-времени и итеративные алгоритмы. Это позволяет моделировать динамику черных дыр, включая столкновения и излучение гравитационных волн, с высокой степенью детализации и точности, что критически важно для проверки предсказаний общей теории относительности и интерпретации астрономических наблюдений. В частности, численные решения необходимы для изучения сильных гравитационных полей вблизи черных дыр, где нелинейные эффекты становятся доминирующими и аналитические подходы терпят неудачу.

Метод характеристического склеивания (Characteristic Gluing) является эффективным подходом к построению пространственно-временных решений, особенно при моделировании динамических процессов, связанных с черными дырами. В основе метода лежит использование двойных нулевых координат (Double Null Coordinates), которые позволяют эффективно моделировать распространение гравитационных волн. Этот выбор координат упрощает решение уравнений Эйнштейна, поскольку позволяет свести задачу к гиперболической системе уравнений в частных производных, что способствует устойчивости и точности численного моделирования. Преимущество заключается в том, что поверхности постоянных координат распространяются со скоростью света, что позволяет напрямую отслеживать распространение волн без необходимости решения эллиптических задач, требующих значительных вычислительных ресурсов.

Для обеспечения высокой точности и устойчивости при численном моделировании пространств-времен вокруг черных дыр, применяются высокопорядочные численные методы, такие как Метод Спектральных Элементов с Непрерывными Галереями (Spectral Element Discontinuous Galerkin Method). Практическая реализация этого метода демонстрирует сходимость порядка 6.20527 для метрики $g_{Ne,n}$ при использовании h-уточнения сетки. Данный порядок сходимости подтверждает эффективность метода в достижении точных решений сложных уравнений общей теории относительности, что критически важно для анализа и моделирования гравитационных волн и других астрофизических явлений.

В процессе «склейки» (gluing) при построении численных решений в общей теории относительности, специальные функции, такие как неполная бета-функция $I_x(a, b)$ , играют ключевую роль. Они необходимы для точного вычисления интегралов, возникающих при сопоставлении данных на границах различных областей пространства-времени. Применение этих функций позволяет обеспечить корректное соединение решений, полученных в разных координатных системах или с использованием различных численных методов. Использование неполной бета-функции обеспечивает точное представление граничных условий и способствует построению реалистичных и физически корректных моделей черных дыр и гравитационных волн, обеспечивая сходимость численных схем и минимизируя ошибки на границах областей вычислений.

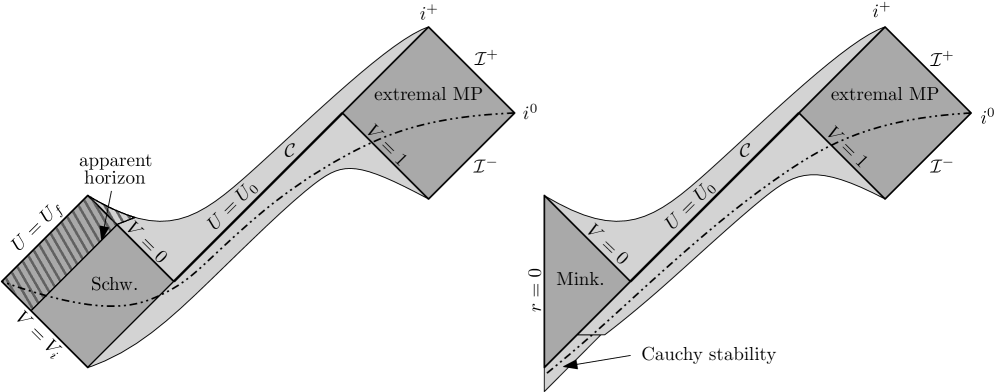
Диаграммы Пенроуза иллюстрируют построение склеек типов (i) и (ii), где темные области соответствуют подмножествам пространств Шварцшильда, ЭМП и Минковского, а светло-затененные области - локальным решениям, полученным из характеристических начально-конечных задач, при этом полосатый узор обозначает захваченную область с горизонтом событий, а устойчивость Коши гарантирует возможность расширения решения до центра симметрии <span class="katex-eq" data-katex-display="false">r=0</span>. — Диаграммы Пенроуза иллюстрируют построение склеек типов (i) и (ii), где темные области соответствуют подмножествам пространств Шварцшильда, ЭМП и Минковского, а светло-затененные области — локальным решениям, полученным из характеристических начально-конечных задач, при этом полосатый узор обозначает захваченную область с горизонтом событий, а устойчивость Коши гарантирует возможность расширения решения до центра симметрии $r=0$ .

Исследование Симметрии и Высших Измерений: Влияние на Понимание Гравитации

Исследование чёрных дыр, обладающих симметриями, таких как чёрная дыра Майерса-Перри, описываемая группами SU(2) и SU(2)xU(1), открывает новые горизонты в понимании их поведения. Симметрии существенно упрощают математическое описание этих объектов, позволяя выявить ключевые характеристики и предсказать их эволюцию. В частности, анализ решений, инваринтных относительно определенных групп симметрий, предоставляет возможность изучать взаимодействие чёрных дыр с материей и гравитационными волнами в более контролируемых условиях. Эти исследования демонстрируют, что симметрии не просто упрощают расчеты, но и отражают фундаментальные свойства пространства-времени вблизи чёрных дыр, указывая на потенциальные связи между симметрией и стабильностью этих экзотических объектов. $R_{\mu\nu} - \frac{1}{2}g_{\mu\nu}R = 0$ — уравнения Эйнштейна, которые эффективно решаются для симметричных решений.

Пространства когомологии-1 представляют собой упрощенную основу для изучения решений уравнений гравитации в высших измерениях. Этот подход позволяет значительно сократить сложность вычислений, сохраняя при этом ключевые физические характеристики исследуемых систем, таких как вращающиеся черные дыры Майерса-Перри. Использование когомологии-1 связано с требованием симметрии, которое ограничивает число независимых переменных, необходимых для описания геометрии пространства-времени. Это позволяет исследователям сосредоточиться на наиболее важных аспектах, таких как поведение горизонта событий и влияние вращения на гравитационное поле. В частности, данный метод оказался полезным при анализе решений, включающих материю Власова и черные дыры Райсснера-Нордстрёма, и позволил получить важные результаты о скорости сходимости численных методов при исследовании нестационарных решений в пятимерном пространстве-времени, подтверждающие возможность формирования черных дыр Майерса-Перри за конечное время.

Исследование решений, включающих власовскую материю и чёрные дыры Райсснера-Нордстрёма, а также их зависимость от безмассовых заряженных скалярных полей, значительно углубляет понимание взаимодействия материи и чёрных дыр. В рамках данной работы рассматривается поведение материи вблизи чёрных дыр, подверженной влиянию скалярных полей, что позволяет изучить динамику аккреции и излучения. Особое внимание уделяется тому, как взаимодействие заряженных скалярных полей с горизонтом событий чёрной дыры модифицирует её структуру и влияет на стабильность решения. Полученные результаты демонстрируют, что подобные взаимодействия могут приводить к формированию новых типов чёрных дыр и существенно изменять их физические характеристики, предлагая новые пути для изучения фундаментальной природы гравитации и материи во Вселенной.

Исследование демонстрирует существование решений вакуумной гравитации в пятимерном пространстве-времени, нарушающих третий закон термодинамики. Анализ метрики fNe,n показал скорость сходимости, равную 6.54804 при h-уточнении, что свидетельствует о быстром приближении к стабильному решению. Дополнительно, экспоненциальная сходимость, подтвержденная значениями p-уточнения 0.58376 и 0.545154, подтверждает надежность численных методов. Эти результаты позволяют предположить возможность формирования чёрных дыр Майерса-Перри за конечное время, что существенно расширяет представления о динамике гравитационных коллапсов в высших измерениях и открывает новые перспективы для изучения фундаментальной природы пространства-времени.

Исследования, проведенные в рамках данной работы, имеют далеко идущие последствия для понимания гравитации в пространствах более высоких размерностей и фундаментальной природы самого пространства-времени. Обнаружение решений, нарушающих третий закон термодинамики, в пятимерном пространстве-времени, подтвержденное высокой скоростью сходимости численных методов $6.54804$ для метрики $fNe,n$ с h-уточнением и экспоненциальной сходимостью, продемонстрированной значениями p-уточнения $0.58376$ и $0.545154$ соответственно, указывает на возможность формирования чёрных дыр Майерса-Перри за конечное время. Эти результаты не только углубляют наше знание о поведении чёрных дыр в более сложных геометриях, но и предоставляют новые инструменты для изучения гравитационных взаимодействий в условиях, не доступных для непосредственного экспериментального наблюдения. Подобные исследования открывают перспективы для построения более полной и адекватной теории гравитации, способной объяснить наблюдаемые космологические явления и предсказать новые физические эффекты.

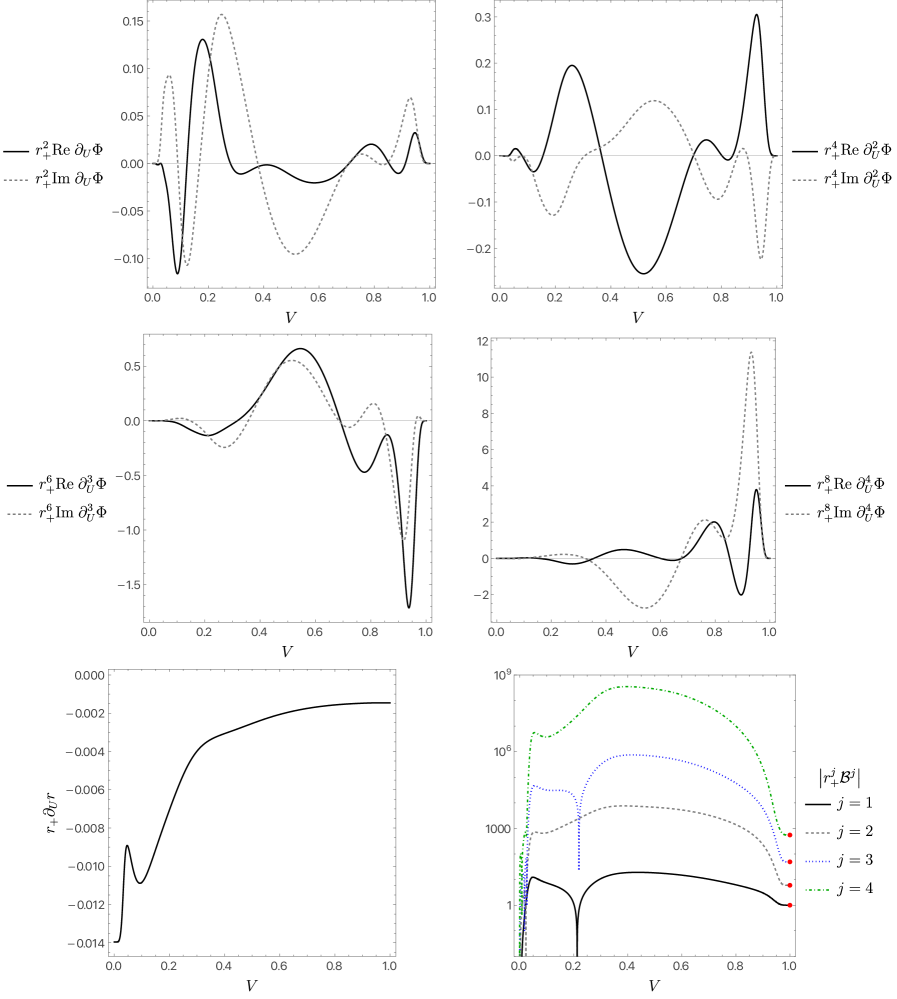
Решение типа (ii) демонстрирует значительные величины производных <span class="katex-eq" data-katex-display="false">\mathcal{B}^{j}</span> (отображенные на логарифмической шкале), достигающие экстремальных значений, при этом красные кружки указывают на значения, соответствующие условиям ЭМП. — Решение типа (ii) демонстрирует значительные величины производных $\mathcal{B}^{j}$ (отображенные на логарифмической шкале), достигающие экстремальных значений, при этом красные кружки указывают на значения, соответствующие условиям ЭМП.

Исследование, представленное в данной работе, демонстрирует, что третье начало чёрной дыры может быть нарушено при определенных условиях, особенно при формировании экстремальных чёрных дыр Майерса-Перри в пяти измерениях. Этот результат подчеркивает сложность и нетривиальность законов, управляющих гравитационным коллапсом. Как однажды заметила Мария Кюри: «Нельзя всегда ждать, чтобы верифицировать истину; нужно искать». Эта фраза отражает подход, используемый в исследовании — активный поиск решений, даже если они противоречат устоявшимся представлениям о третьем начале чёрной дыры. Понимание условий, при которых это нарушение происходит, открывает новые возможности для изучения экстремальных гравитационных систем и углубляет наше понимание фундаментальной физики.

Куда Ведут Эти Пути?

Представленные результаты, демонстрирующие нарушение третьего закона чёрных дыр в вакуумной гравитации, скорее обнажают внутренние противоречия в самой формулировке, нежели опровергают его окончательно. Если система держится на костылях, значит, мы переусложнили её. Попытки спасти закон, добавляя всё новые и новые постулаты о «недостижимости» экстремальных чёрных дыр, напоминают попытки залатать дырявое судно — временное облегчение, но не решение проблемы. Важно понимать, что нарушение закона — это не ошибка в вычислениях, а сигнал о том, что наше фундаментальное понимание экстремальных гравитационных систем нуждается в пересмотре.

Модульность, столь привлекательная в теоретических построениях, без понимания контекста — иллюзия контроля. Конструирование решений для чёрных дыр Майерса-Перри в пяти измерениях — важный шаг, но он лишь указывает на необходимость более глубокого исследования динамических процессов, приводящих к формированию этих объектов. Необходимо отойти от статических решений и исследовать эволюцию чёрных дыр в более реалистичных сценариях гравитационного коллапса, учитывая влияние возмущений и обратной связи.

В конечном счёте, задача состоит не в том, чтобы «спасти» третий закон, а в том, чтобы понять, что он пытается нам сказать о природе экстремальных гравитационных систем. Возможно, нарушение этого закона — это не аномалия, а ключ к пониманию более глубокой, более элегантной теории гравитации, где понятие «недостижимости» уступает место более естественному описанию динамики чёрных дыр.

Оригинал статьи: https://arxiv.org/pdf/2601.20955.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-01 08:42