Предвестники конденсации в мире калибровочных фермионных теорий

Автор: Денис Аветисян

Новое исследование с использованием функциональной ренормализационной группы раскрывает механизм формирования предконденсата — структуры, зарождающейся лишь на конечном масштабе длин — в системах, где важны взаимодействия калибровочных и фермионных полей.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал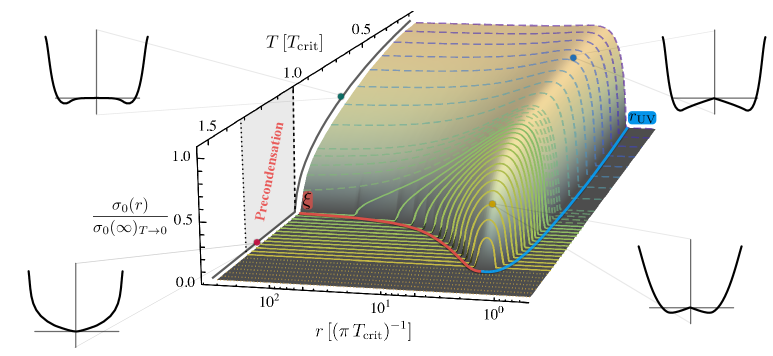

В рамках теории калибровочных фермионов, подобной КХД с <span class="katex-eq" data-katex-display="false">N_c = 3</span> и <span class="katex-eq" data-katex-display="false">N_f = 3</span> хиральными вкусами, порядок хирального параметра <span class="katex-eq" data-katex-display="false">\sigma_0(r)</span> демонстрирует зависимость от пространственного разделения <i>r</i> и температуры, при этом наблюдается исчезновение конденсата при высоких температурах и формирование макроскопического конденсата на больших расстояниях в фазе спонтанного нарушения симметрии, а в предконденсатном режиме - конденсата, существующего лишь в ограниченном диапазоне масштабов длин, определяемом длиной корреляции ξ и ультрафиолетовой длиной <span class="katex-eq" data-katex-display="false">r_{UV}</span>. — В рамках теории калибровочных фермионов, подобной КХД с $N_c = 3$ и $N_f = 3$ хиральными вкусами, порядок хирального параметра $\sigma_0(r)$ демонстрирует зависимость от пространственного разделения r и температуры, при этом наблюдается исчезновение конденсата при высоких температурах и формирование макроскопического конденсата на больших расстояниях в фазе спонтанного нарушения симметрии, а в предконденсатном режиме — конденсата, существующего лишь в ограниченном диапазоне масштабов длин, определяемом длиной корреляции ξ и ультрафиолетовой длиной $r_{UV}$ .

Работа посвящена исследованию предконденсации в калибровочных фермионных теориях при конечных температурах с использованием методов функциональной ренормализационной группы, показывая ее усиление с увеличением числа вкусов и связь с конкурирующими процессами нарушения и восстановления симметрии.

Несмотря на значительный прогресс в понимании фазовых переходов, механизм формирования конденсатов на ограниченных масштабах длины остается малоизученным. В работе ‘Thermal precondensation in gauge-fermion theories’ исследуется явление преконденсации в калибровочно-фермионных теориях вблизи теплового перехода, связанного с нарушением хиральной симметрии. Показано, что преконденсация усиливается с увеличением числа ароматов фермионов и обусловлена соревнованием между процессами нарушения и восстановления симметрии. Может ли данный феномен пролить свет на физику за пределами Стандартной модели и открыть новые пути для исследования непертурбативных эффектов в квантовой теории поля?

За гранью Традиционных Фазовых Переходов: Новая Перспектива

Традиционное представление о спонтанном нарушении хиральной симметрии предполагает резкий переход между симметричной и фазой с нарушенной симметрией, однако всё больше данных свидетельствуют о том, что это не всегда так. В ряде случаев наблюдается постепенное нарушение симметрии, когда переход не является мгновенным и чётким. Вместо этого, система может демонстрировать промежуточное состояние, где симметрия нарушается лишь частично и неравномерно в пространстве. Это отклонение от классической картины требует пересмотра существующих теоретических моделей и разработки новых подходов к описанию фазовых переходов, учитывающих более сложные сценарии нарушения симметрии, отличные от простого «включено-выключено». Исследование подобных явлений открывает новые возможности для понимания фундаментальных свойств материи в экстремальных условиях.

Всё больше данных свидетельствует о существовании промежуточной фазы, где хиральная симметрия нарушается не полностью, а частично, проявляясь в виде пространственных неоднородностей. Вместо резкого перехода от симметричного к нарушенному состоянию, наблюдается область, где симметрия спонтанно нарушается лишь в отдельных областях пространства, формируя домены различной фазы. Эти домены, часто называемые областями предконденсации, характеризуются локальным нарушением симметрии, окружённым областями, где симметрия сохраняется. Изучение этой сложной пространственной структуры требует новых подходов к анализу, учитывающих взаимосвязь между локальными флуктуациями и глобальными свойствами системы, а также влияние различных степеней свободы на формирование этих неоднородностей. Понимание этой фазы предконденсации открывает новые возможности для изучения критических явлений и фазовых переходов в физике высоких энергий и конденсированных сред.

Для адекватного описания режима “предконденсации”, когда симметрия нарушается лишь частично и пространственно неоднородно, требуется разработка новых теоретических подходов, выходящих за рамки стандартной теории фазовых переходов. Традиционные методы, основанные на анализе однородных систем, оказываются недостаточными для описания возникающих сложных структур и флуктуаций. Исследователи фокусируются на изучении коллективных степеней свободы, таких как топологические дефекты и доменные границы, которые играют ключевую роль в формировании этого промежуточного режима. Особое внимание уделяется развитию функциональных методов, способных учитывать сильные корреляции и нелокальные взаимодействия между частицами, что позволяет получить более точное представление о свойствах системы вблизи точки фазового перехода и в области “предконденсации”. Понимание этих механизмов открывает перспективы для создания новых материалов с необычными свойствами и управления фазовыми переходами на наноуровне.

В зависимости от температуры, система проходит через стадии флуктуаций, преконденсации с локальным образованием конденсата на масштабах ξ и формирования однородного макроскопического конденсата при температурах ниже <span class="katex-eq" data-katex-display="false">T_{crit}</span>. — В зависимости от температуры, система проходит через стадии флуктуаций, преконденсации с локальным образованием конденсата на масштабах ξ и формирования однородного макроскопического конденсата при температурах ниже $T_{crit}$ .

Неоднородные Конденсаты: Проявление Предконденсации

Предконденсация характеризуется формированием неоднородных конденсатов, в которых плотность конденсированных частиц не является постоянной в пространстве. Вместо этого наблюдается пространственная вариация плотности, приводящая к образованию доменов с различной концентрацией конденсированных частиц. Данный процесс отличается от классической конденсации, где формируется однородный конденсат с равномерной плотностью по всему объему. Неоднородность возникает из-за флуктуаций плотности и взаимодействия между частицами, что приводит к локальному накоплению и формированию доменов различного размера и формы. $\rho(r) \neq const$ , где $\rho(r)$ — плотность конденсированных частиц в точке $r$ .

Размер неоднородностей — доменная структура — играет определяющую роль в характеристике промежуточной фазы предконденсации. Влияние размера доменов проявляется в масштабировании различных физических величин, включая энергию поверхности и критические явления. При малых размерах доменов преобладают флуктуации, а свойства системы приближаются к однородным. С увеличением размера доменов возрастает вклад долгозатных корреляций, что приводит к изменению критических показателей и формированию специфической структуры конденсированной фазы. В частности, зависимость энергии от размера домена описывается соотношением $E \propto L^{-d}$ , где $L$ — характерный размер домена, а $d$ — размерность системы. Таким образом, контроль над размером доменов позволяет управлять свойствами и стабильностью предконденсатных структур.

В процессе прекондесации, когда формируются неоднородные конденсаты, наблюдается появление конденсатов, зависимых от импульса. Данное явление обусловлено изменением дисперсионных соотношений $E(k)$ в фазе прекондесации, где $E$ — энергия, а $k$ — волновой вектор. Изменение дисперсии приводит к тому, что частицы с разными импульсами конденсируются в различных областях пространства, формируя пространственно-зависимую плотность конденсата. В отличие от однородного конденсата, где все частицы находятся в состоянии с нулевым импульсом, в данном случае конденсация происходит не в одном, а в нескольких импульсных состояниях, определяемых локальной формой дисперсионной кривой.

Зависимость размера домена от температуры, нормированной на критическую, демонстрирует, что при <span class="katex-eq" data-katex-display="false">N_f = 2, 3, 4</span> наблюдаются соответствующие закономерности (обозначены фиолетовым, синим и зеленым цветами, см. также рисунки 1 и 5), а вставка показывает, как уменьшенная температура предконденсации зависит от обратной величины <span class="katex-eq" data-katex-display="false">N_f^{-1}</span>. — Зависимость размера домена от температуры, нормированной на критическую, демонстрирует, что при $N_f = 2, 3, 4$ наблюдаются соответствующие закономерности (обозначены фиолетовым, синим и зеленым цветами, см. также рисунки 1 и 5), а вставка показывает, как уменьшенная температура предконденсации зависит от обратной величины $N_f^{-1}$ .

Функциональная Ренормализационная Группа: Непертурбативный Подход к Пониманию

Для исследования предконденсации используется функциональная ренормализационная группа (ФРГ), непертурбативный метод, особенно эффективный при анализе систем с сильными корреляциями. В отличие от традиционных методов, основанных на разложении в ряд, ФРГ позволяет изучать системы, где взаимодействие между частицами не является слабым, и приближения могут быть неприменимы. Данный подход основан на последовательном “интегрировании” степеней свободы, начиная с высоких энергий и опуская их по мере уменьшения масштаба, что позволяет получить информацию о фазовых переходах и критическом поведении системы без необходимости введения априорных упрощений.

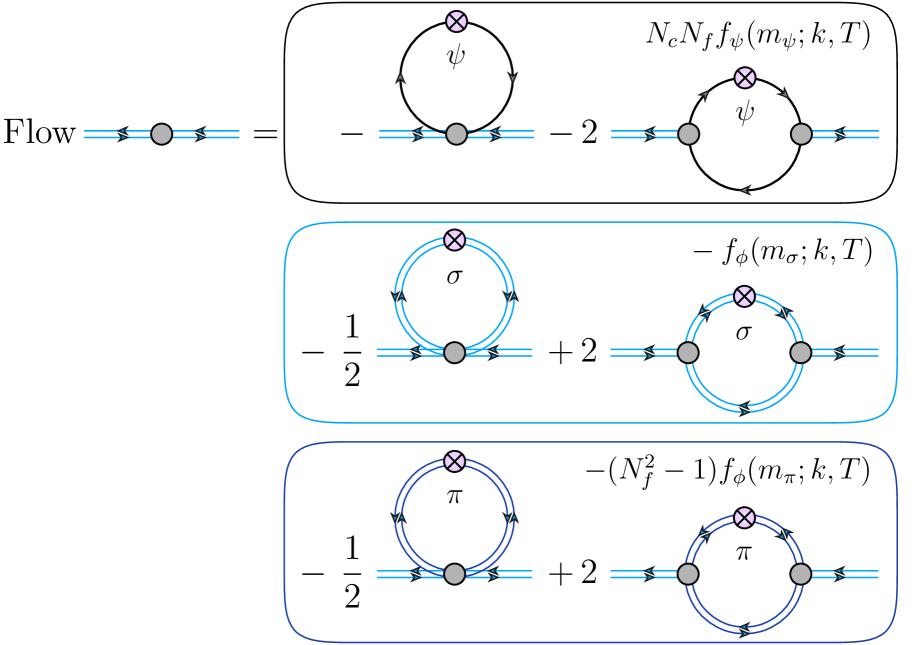
Функциональная ренормализационная группа (ФРГ) позволяет исследовать системы калибровочных фермионов — теоретическую основу для понимания фазовых переходов — без использования приближений, типичных для стандартных методов. В отличие от perturbative подходов, ФРГ оперирует с полным эффективным действием, позволяя учитывать все возможные взаимодействия между частицами. Это особенно важно при исследовании сильнокоррелированных систем, где perturbative разложения не сходятся. ФРГ строит поток эффективного действия в зависимости от масштаба энергии, позволяя проследить эволюцию системы от ультрафиолетовой до инфракрасной области и выявить критические точки, определяющие фазовые переходы, без априорных ограничений, связанных с выбором конкретного приближения.

Применение функциональной ренормализационной группы (ФРГ) позволяет построить фазовую диаграмму системы и определить условия, при которых возникает преконденсация. Метод ФРГ, в отличие от пертурбативных подходов, не требует введения упрощающих приближений и позволяет исследовать фазовые переходы в сильнокоррелированных системах. Анализ функционала эффективного действия $\Gamma_k$ при изменении масштаба $k$ позволяет выявить критические параметры и области стабильности различных фаз, включая фазу преконденсации, характеризующуюся специфическими корреляционными свойствами и предшествующую основному фазовому переходу.

Диаграмма радиальной двухточечной функции σ-моды демонстрирует кривизну эффективного потенциала при малых полях, что указывает на формирование конденсата, где двойные стрелки обозначают полные пропагаторы σ- и <span class="katex-eq" data-katex-display="false">\bm{\pi}</span>-мод, одинарные - пропагаторы фермионов, серые точки - полные вершины, а перекрещенные круги - вставки производной регуляторной функции по масштабу, что стандартно для функционального ренормализационной группы. — Диаграмма радиальной двухточечной функции σ-моды демонстрирует кривизну эффективного потенциала при малых полях, что указывает на формирование конденсата, где двойные стрелки обозначают полные пропагаторы σ- и $\bm{\pi}$ -мод, одинарные — пропагаторы фермионов, серые точки — полные вершины, а перекрещенные круги — вставки производной регуляторной функции по масштабу, что стандартно для функционального ренормализационной группы.

Роль Nf и Nc: Влияние Параметров на Фазовый Переход

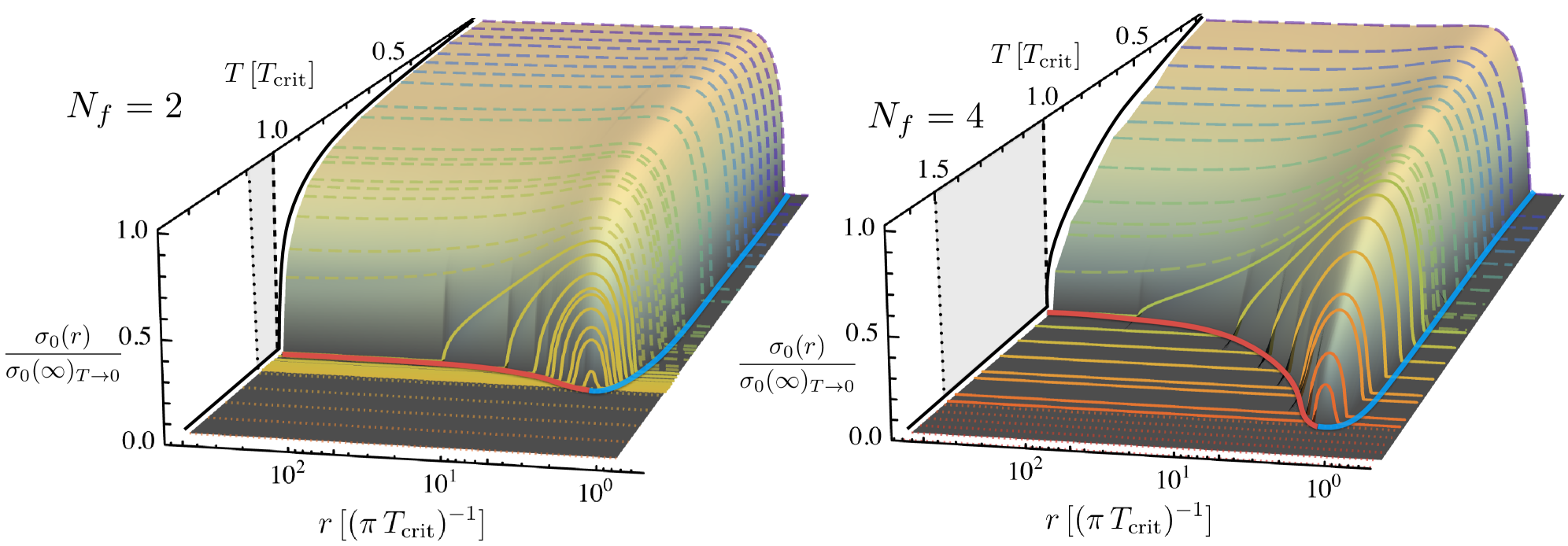
Количество фермионных ароматов (Nf) и цветов (Nc) оказывает существенное влияние на поведение системы, определяя условия формирования предконденсата. Исследования показывают, что изменение этих параметров приводит к заметным изменениям в фазовом переходе. В частности, увеличение числа ароматов способствует расширению температурного интервала, в котором наблюдается предконденсация — предварительное формирование упорядоченной фазы перед полным фазовым переходом. Этот эффект обусловлен усилением флуктуаций фермионов, которые играют ключевую роль в спонтанном нарушении хиральной симметрии и формировании коллективного поведения частиц. Понимание взаимосвязи между Nf, Nc и предконденсацией критически важно для изучения свойств адронной материи в экстремальных условиях, например, в недрах нейтронных звезд или в первые моменты после Большого Взрыва.

В данной системе наблюдается сложное взаимодействие между фермионными и бозонными флуктуациями, определяющее фазовый переход. Фермионные флуктуации, связанные с самопроизвольным нарушением хиральной симметрии, стремятся к образованию конденсированной фазы. В то же время, бозонные флуктуации, напротив, способствуют восстановлению симметрии, ослабляя тенденцию к конденсации. Именно баланс между этими конкурирующими процессами и задает характер фазового перехода, определяя температуру и свойства возникающей фазы. $\langle \bar{\psi} \psi \rangle$ — величина, характеризующая нарушение хиральной симметрии, напрямую зависит от соотношения между фермионными и бозонными возбуждениями.

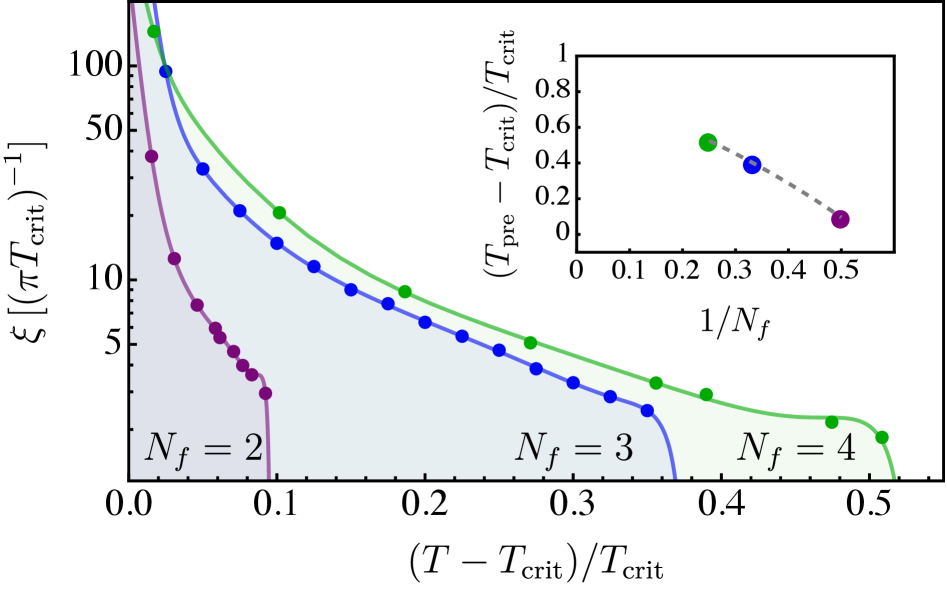
Проведенный анализ, охватывающий значения числа фермионных ароматов (Nf) равные 2, 3 и 4, выявил отчетливую закономерность: температурный интервал, в котором наблюдается предконденсация, увеличивается с ростом Nf. Данное наблюдение указывает на то, что увеличение числа фермионных степеней свободы способствует более широкому диапазону температур, в котором система проявляет признаки спонтанного нарушения хиральной симметрии перед полным фазовым переходом. Иными словами, чем больше ароматов фермионов участвует в процессе, тем более «размытым» становится переход, и тем шире температурная область, в которой можно наблюдать зародыши нового фазового состояния, предшествующего полной конденсации.

Анализ параметра хирального порядка <span class="katex-eq" data-katex-display="false">\sigma_0(r)</span> для двух теорий типа КХД с <span class="katex-eq" data-katex-display="false">N_c = 3</span> и различным числом хиральных ароматов (<span class="katex-eq" data-katex-display="false">N_f = 2</span> слева и <span class="katex-eq" data-katex-display="false">N_f = 4</span> справа) показывает его зависимость от пространственного разделения <span class="katex-eq" data-katex-display="false">r</span> и температуры, нормированной к значению при нулевой температуре в макроскопическом пределе. — Анализ параметра хирального порядка $\sigma_0(r)$ для двух теорий типа КХД с $N_c = 3$ и различным числом хиральных ароматов ( $N_f = 2$ слева и $N_f = 4$ справа) показывает его зависимость от пространственного разделения $r$ и температуры, нормированной к значению при нулевой температуре в макроскопическом пределе.

Перспективы для Понимания Сильных Взаимодействий: От Теории к Реальности

Результаты функционального ренормализационной группы (ФРГ) позволяют получить ценные сведения о природе спонтанного нарушения хиральной симметрии и преконденсации в сильно коррелированных системах. Исследование показывает, что нарушение симметрии происходит не мгновенно, а постепенно, с формированием предварительной конденсации, характеризующейся появлением порядка до достижения критической температуры. $\langle \bar{q}q \rangle$ является ключевым индикатором этого процесса, демонстрируя изменение знака и увеличение модуля по мере приближения к фазовому переходу. Данный механизм играет важную роль в понимании формирования динамической массы кварков и адронов в квантовой хромодинамике (КХД), а также может быть применен к другим физическим системам, где наблюдаются подобные явления, таким как сверхпроводимость и магнетизм.

Эффективный потенциал представляет собой мощный аналитический инструмент для изучения фазовых переходов, особенно в контексте сильных взаимодействий. Данный подход позволяет исследовать изменение состояния системы при изменении температуры и других параметров, выявляя критические точки и характер спонтанного нарушения хиральной симметрии. Изучение формы эффективного потенциала, $V_{eff}(\phi)$ , где φ — хиральный порядок, позволяет определить стабильность различных фаз и предсказать поведение системы вблизи критических точек. По сути, эффективный потенциал отображает энергетическую стоимость формирования хирального конденсата и определяет, при каких условиях эта конденсация станет энергетически выгодной, приводя к изменению свойств системы и появлению новых фаз материи.

Полученные результаты имеют далеко идущие последствия для понимания свойств квантовой хромодинамики (КХД) и других систем, демонстрирующих схожие явления. Исследование позволяет глубже взглянуть на механизмы спонтанного нарушения хиральной симметрии — фундаментальный аспект КХД, определяющий массу адронов и поведение кварк-глюонной плазмы. Аналогичные принципы применимы к изучению сверхпроводимости и других конденсированных сред, где коллективное поведение частиц приводит к возникновению новых фаз материи. Таким образом, разработанный подход открывает перспективы для унифицированного описания широкого спектра физических систем, от элементарных частиц до макроскопических объектов, способствуя прогрессу в теоретической физике и материаловедении.

Исследование, представленное в данной работе, демонстрирует, что предконденсация, формирующаяся на конечных масштабах длины, усиливается с увеличением числа ароматов. Этот процесс тесно связан с конкурирующими динамиками нарушения и восстановления симметрии. Нельзя утверждать, что полученные результаты — абсолютная истина, скорее, это приближение к реальности, полученное посредством анализа данных. Как справедливо заметил Джон Локк: «Ум — это пустая шкатулка» (лат. Tabula rasa). Данное утверждение особенно актуально в контексте функционального ренормализационного подхода, где исходные условия и выбор модели неизбежно влияют на конечные результаты. Представленный анализ — не открытие истины, а лишь один из способов её аппроксимации, требующий дальнейшей проверки и уточнения.

Куда двигаться дальше?

Представленная работа, исследуя феномен преконденсации в калибровочно-фермионных теориях, лишь осторожно очерчивает границы понимания. Необходимо признать, что зависимость от используемого приближения функциональной ренормализационной группы вносит определенную неопределенность в полученные результаты. Насколько устойчивы наблюдаемые эффекты к изменениям в схеме регуляризации? Этот вопрос, безусловно, требует дальнейшей проработки. Более того, связь между преконденсацией и динамикой восстановления симметрии, хотя и намечена, нуждается в более детальном количественном анализе, особенно в условиях, далеких от предельного случая бесконечного числа вкусов.

Особое внимание следует уделить проверке полученных результатов на конкретных моделях физики элементарных частиц. Насколько универсальна концепция преконденсации, и проявляется ли она в тех же формах в различных калибровочных теориях? Может ли она играть роль в понимании механизмов, лежащих в основе хирального симметроломления в адронной физике? Эти вопросы, вероятно, потребуют не только теоретических, но и феноменологических исследований, сопоставления с данными экспериментов по столкновениям тяжелых ионов.

Наконец, необходимо помнить о фундаментальном ограничении — любая модель является лишь упрощением реальности. Преконденсация, возможно, лишь одна из многих форм коллективного поведения, возникающих в сложных системах. Истина, вероятно, кроется не в поиске единственного объяснения, а в построении иерархии моделей, каждая из которых описывает определенный аспект явления. Именно в этой последовательной проверке и сомнении, а не в поспешных выводах, и заключается подлинный прогресс.

Оригинал статьи: https://arxiv.org/pdf/2602.11265.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-14 18:21