Пространственные узоры в мире сильных взаимодействий

Автор: Денис Аветисян

Новое исследование демонстрирует, как локальные неоднородности определяют эволюцию квантовых систем после резкого изменения параметров.

Динамика двойной заполненности после резкого изменения параметров взаимодействия показывает, что в зависимости от силы этого изменения (<span class="katex-eq" data-katex-display="false">U_f</span>) наблюдается различная эволюция во времени и пространстве, при этом период колебаний (<span class="katex-eq" data-katex-display="false">\mathcal{T}</span>) и усредненная двойная заполненность (<span class="katex-eq" data-katex-display="false">D^{\*}</span>) демонстрируют четкую зависимость от соотношения <span class="katex-eq" data-katex-display="false">U_f/W</span>, что позволяет исследовать закономерности, определяющие поведение системы после возмущения. — Динамика двойной заполненности после резкого изменения параметров взаимодействия показывает, что в зависимости от силы этого изменения ( $U_f$ ) наблюдается различная эволюция во времени и пространстве, при этом период колебаний ( $\mathcal{T}$ ) и усредненная двойная заполненность ( $D^{\*}$ ) демонстрируют четкую зависимость от соотношения $U_f/W$ , что позволяет исследовать закономерности, определяющие поведение системы после возмущения.

Исследование динамики неравновесных систем в рамках Хаббардовской модели с использованием приближения зависимого от времени Гатцвиллера (Time-dependent Gutzwiller approximation) и метода DMFT.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал

Несмотря на успехи в изучении неравновесной динамики сильно коррелированных электронных систем, пространственная неоднородность часто упускается из виду. В работе ‘Emergent Spatial Textures from Interaction Quenches in the Hubbard Model’ исследуется влияние мгновенного изменения взаимодействия в полузаполненной модели Хаббарда с использованием приближения зависящего от времени Гютцвиллера в реальном пространстве. Показано, что даже слабые пространственные флуктуации растут со временем, приводя к самоорганизации системы в неоднородные моттовские домены. Может ли формирование пространственных текстур представлять собой фундаментальное ограничение для теоретических подходов, предполагающих пространственную однородность, и как это влияет на понимание динамики сильно коррелированных материалов вдали от равновесия?

За пределами равновесия: Исследование динамики «нуллибриума»

Традиционная физика конденсированного состояния, как правило, оперирует понятием равновесия, что существенно ограничивает возможности описания систем, подверженных внешнему воздействию или находящихся в неравновесных условиях. Этот подход, хотя и эффективен для многих материалов, не позволяет адекватно исследовать динамические процессы, возникающие под действием света, тепла или электрических полей. Ограниченность равновесного подхода особенно заметна при изучении взаимодействующих квантовых систем, где внешнее воздействие может привести к возникновению новых фаз материи и сложных коллективных явлений, не предсказываемых в рамках статической теории. Понимание поведения систем вдали от равновесия требует разработки новых теоретических моделей и экспериментальных методов, способных уловить быстропротекающие процессы и нелинейные эффекты, определяющие их свойства.

Исследование систем, находящихся вдали от равновесия, описываемых как “нуллибриумная динамика”, имеет первостепенное значение для понимания фундаментальных процессов и открытия новых состояний материи. Традиционные подходы, основанные на предположении о равновесии, часто оказываются недостаточными для адекватного описания систем, подверженных внешнему воздействию или взаимодействию. Именно вдали от равновесия проявляются сложные коллективные эффекты и возникают неожиданные фазы материи, которые не могут быть предсказаны на основе статических свойств. Изучение этих динамических процессов позволяет получить более полное представление о природе материи и открыть возможности для создания новых материалов с уникальными свойствами, например, сверхпроводников нового типа или квантовых устройств с улучшенными характеристиками. Понимание принципов нуллибриумной динамики становится ключевым для развития современной физики конденсированного состояния и квантовой науки.

Особое значение динамика, далекая от равновесия, приобретает при изучении взаимодействующих квантовых систем, в частности, тех, что описываются моделью Хаббарда. Данная модель, являясь фундаментальной для понимания поведения электронов в твердых телах, позволяет исследовать сложные явления, возникающие из-за кулоновского взаимодействия между ними. В условиях, когда система подвергается внешнему воздействию или находится в неравновесном состоянии, традиционные методы, основанные на предположении о равновесии, оказываются неприменимыми. Исследование динамики модели Хаббарда вдали от равновесия позволяет выявить новые фазы материи и понять механизмы, определяющие ее свойства, например, высокотемпературную сверхпроводимость и магнетизм. Понимание этих процессов требует разработки новых теоретических подходов и экспериментальных методов, способных зафиксировать быстропротекающие изменения в квантовых системах.

Для исследования динамики систем, далеких от равновесия, необходимы передовые экспериментальные методы, такие как ультрабыстрая спектроскопия. Данная техника позволяет «заморозить» мгновенные изменения в материалах, происходящие на фемтосекундных временных масштабах — триллионных долях секунды. Используя сверхкороткие световые импульсы, ученые могут возбуждать исследуемый материал и отслеживать эволюцию его состояния, фиксируя промежуточные этапы, которые невозможно наблюдать в стационарных условиях. Это особенно важно для понимания поведения сложных квантовых систем, таких как модели Хаббарда, где взаимодействие между частицами определяет их коллективные свойства и динамику. $\Delta t \ll \tau_{relax}$ , где $\Delta t$ — длительность импульса, а $\tau_{relax}$ — время релаксации системы, является ключевым условием успешного применения данного метода.

Динамика спектрального веса, усредненного по сайтам, <span class="katex-eq" data-katex-display="false">\mathcal{Z}(t)</span>, после взаимодействия, приводящего к конечному значению силы <span class="katex-eq" data-katex-display="false">U_f</span>, демонстрирует зависимость от силы взаимодействия: слабые, умеренные и сильные взаимодействия приводят к различным траекториям изменения спектрального веса, а усредненный спектральный вес <span class="katex-eq" data-katex-display="false">\langle\mathcal{Z}\rangle</span> зависит от отношения <span class="katex-eq" data-katex-display="false">U_f/W</span>. — Динамика спектрального веса, усредненного по сайтам, $\mathcal{Z}(t)$ , после взаимодействия, приводящего к конечному значению силы $U_f$ , демонстрирует зависимость от силы взаимодействия: слабые, умеренные и сильные взаимодействия приводят к различным траекториям изменения спектрального веса, а усредненный спектральный вес $\langle\mathcal{Z}\rangle$ зависит от отношения $U_f/W$ .

Квантовые скачки: Вывод системы из равновесия

Квантовый скачок (quantum quench) представляет собой резкое изменение одного из параметров квантовой системы, приводящее к отходу от начального состояния равновесия. Это изменение должно быть достаточно быстрым, чтобы система не успела адаптироваться к новому значению параметра посредством адиабатического процесса. В результате происходит возбуждение системы и возникновение не-равновесных динамических процессов, характеризующихся временной эволюцией корреляций и распределения энергии. Данный подход позволяет изучать поведение систем вне равновесия и исследовать фундаментальные вопросы о динамике квантовых систем, особенно в контексте сильно взаимодействующих систем и тех, которые характеризуются пространственной неоднородностью.

Резкое изменение параметров квантовой системы, известное как квантовый сдвиг, приводит к возникновению сложной динамики, характеризующейся временной эволюцией корреляций между различными степенями свободы системы. В отличие от равновесных систем, где корреляции обычно описываются статическими величинами, в случае квантового сдвига эти корреляции становятся функциями времени, отражая не-равновесный характер процесса. Исследование этой временной эволюции позволяет выявить механизмы релаксации и установления новых корреляций, а также определить скорость, с которой система приближается к новому, возможно, не-равновесному состоянию. Анализ динамики корреляций требует использования методов, способных учесть как взаимодействия между частицами, так и пространственную неоднородность системы, что делает данный подход ценным инструментом для изучения не-равновесной физики конденсированного состояния.

Однополосная модель Хаббарда (Single-Band Hubbard Model) представляет собой упрощенную, но эффективную теоретическую основу для изучения динамики квантовых скачков. Она позволяет анализировать взаимодействие между электронами в кристаллической решетке, учитывая как кинетическую энергию, так и кулоновское отталкивание. Метод Фашбаха (Feshbach Tuning) предоставляет возможность контролировать силу взаимодействия между частицами, изменяя внешнее магнитное поле и, таким образом, настраивая систему в различных режимах. Это позволяет исследовать переход от слабовзаимодействующих к сильновзаимодействующим системам, что особенно важно для понимания динамики после квантового скачка и изучения формирования корреляций между частицами. $H = -t \sum_{\langle i,j \rangle} (c^{\dagger}_i c_j + c^{\dagger}_j c_i) + U \sum_i n_i^2$ — основное выражение модели, где $t$ — интеграл перескока, $U$ — энергия кулоновского взаимодействия, а $n_i$ — оператор числа частиц на узле решетки.

Изучение динамики, возникающей при квантовых сдвигах, требует применения теоретических подходов, способных адекватно учитывать сильные взаимодействия между частицами и пространственную неоднородность системы. Традиционные методы теории возмущений часто оказываются неприменимы в условиях сильных взаимодействий, что обуславливает необходимость использования непертурбативных техник, таких как метод динамической теории среднего поля (DMFT) или квантово-монтаж-карлссона (QMC). Пространственная неоднородность, возникающая, например, в виде локализованных дефектов или градиентов параметров, требует учета корреляций на больших расстояниях и может приводить к формированию новых фаз или экзотических состояний вещества. Для адекватного описания таких систем необходимо разрабатывать и применять численные методы, способные эффективно моделировать многочастичные квантовые системы с сильными взаимодействиями и пространственной неоднородностью.

После быстрого изменения параметров системы наблюдается формирование доменов с последующим укрупнением, что проявляется во временной эволюции средней двойной заполненности <span class="katex-eq" data-katex-display="false">\mathcal{D}(t)</span>, ее пространственного стандартного отклонения <span class="katex-eq" data-katex-display="false">\sigma_{\mathcal{D}}(t)</span> и флуктуаций плотности <span class="katex-eq" data-katex-display="false">\sigma_{n}(t)</span>, а также в изменениях локальной двойной заполненности <span class="katex-eq" data-katex-display="false">\mathcal{D}_{i}</span> (иллюстрируется на моментах времени, представленных на рисунке и в соответствующих вставках). — После быстрого изменения параметров системы наблюдается формирование доменов с последующим укрупнением, что проявляется во временной эволюции средней двойной заполненности $\mathcal{D}(t)$ , ее пространственного стандартного отклонения $\sigma_{\mathcal{D}}(t)$ и флуктуаций плотности $\sigma_{n}(t)$ , а также в изменениях локальной двойной заполненности $\mathcal{D}_{i}$ (иллюстрируется на моментах времени, представленных на рисунке и в соответствующих вставках).

Пространственная динамика: Раскрытие пространственной неоднородности

Реализация приближения во времени и в пространстве Гуцвиллера (TDGA) представляет собой эффективный инструмент для моделирования динамики сильно коррелированных систем с пространственным разрешением. В отличие от методов, оперирующих в импульсном пространстве или предполагающих однородность системы, TDGA позволяет отслеживать эволюцию локальных величин, таких как плотность и фаза волновой функции, непосредственно в реальном пространстве. Это достигается путем решения $i\hbar \frac{\partial}{\partial t} |\psi(r,t)\rangle = H(t) |\psi(r,t)\rangle$ для локализованной волновой функции $|\psi(r,t)\rangle$ , где $H(t)$ — гамильтониан системы, зависящий от времени. Такой подход особенно полезен для исследования систем с пространственными неоднородностями, такими как те, что возникают в результате быстрого изменения параметров системы (quench), или в неоднородных потенциалах. Вычислительная сложность TDGA масштабируется с количеством пространственных точек, что делает его применимым к системам умеренного размера, но позволяет получать детальную информацию о локальной динамике, недоступную для других методов.

Метод, основанный на приближении Гутцвиллерa, позволяет отслеживать формирование пространственных неоднородностей и изучать их влияние на поведение системы. В рамках этого подхода, локальные функции волновой функции и параметры, характеризующие корреляции, вычисляются на каждой точке решетки, что дает возможность наблюдать за развитием неоднородностей во времени и пространстве. Анализ этих неоднородностей, таких как области, демонстрирующие моттовское поведение, позволяет понять, как локальные корреляции влияют на макроскопические свойства системы и как эти свойства изменяются под воздействием внешних факторов, например, быстрого изменения параметров системы (quench).

Динамика Гатцвиллера-фон Неймана (Gutzwiller von Neumann Dynamics) представляет собой надежный и точный вычислительный фреймворк, реализующий уравнение фон Неймана в рамках временной зависимой аппроксимации Гатцвиллера (TDGA). Этот подход позволяет моделировать эволюцию во времени сильнокоррелированных систем с учетом пространственного разрешения. В основе метода лежит решение $i\hbar \frac{d}{dt} \rho = [\hat{H}, \rho]$ , где ρ — матрица плотности, а $\hat{H}$ — гамильтониан системы, при этом аппроксимация Гатцвиллера используется для упрощения расчета матричных элементов и описания локальных корреляций. В результате, динамика Гатцвиллера-фон Неймана обеспечивает эффективный инструмент для исследования не равновесной динамики квантовых систем, в частности, для моделирования процессов, приводящих к образованию пространственных неоднородностей.

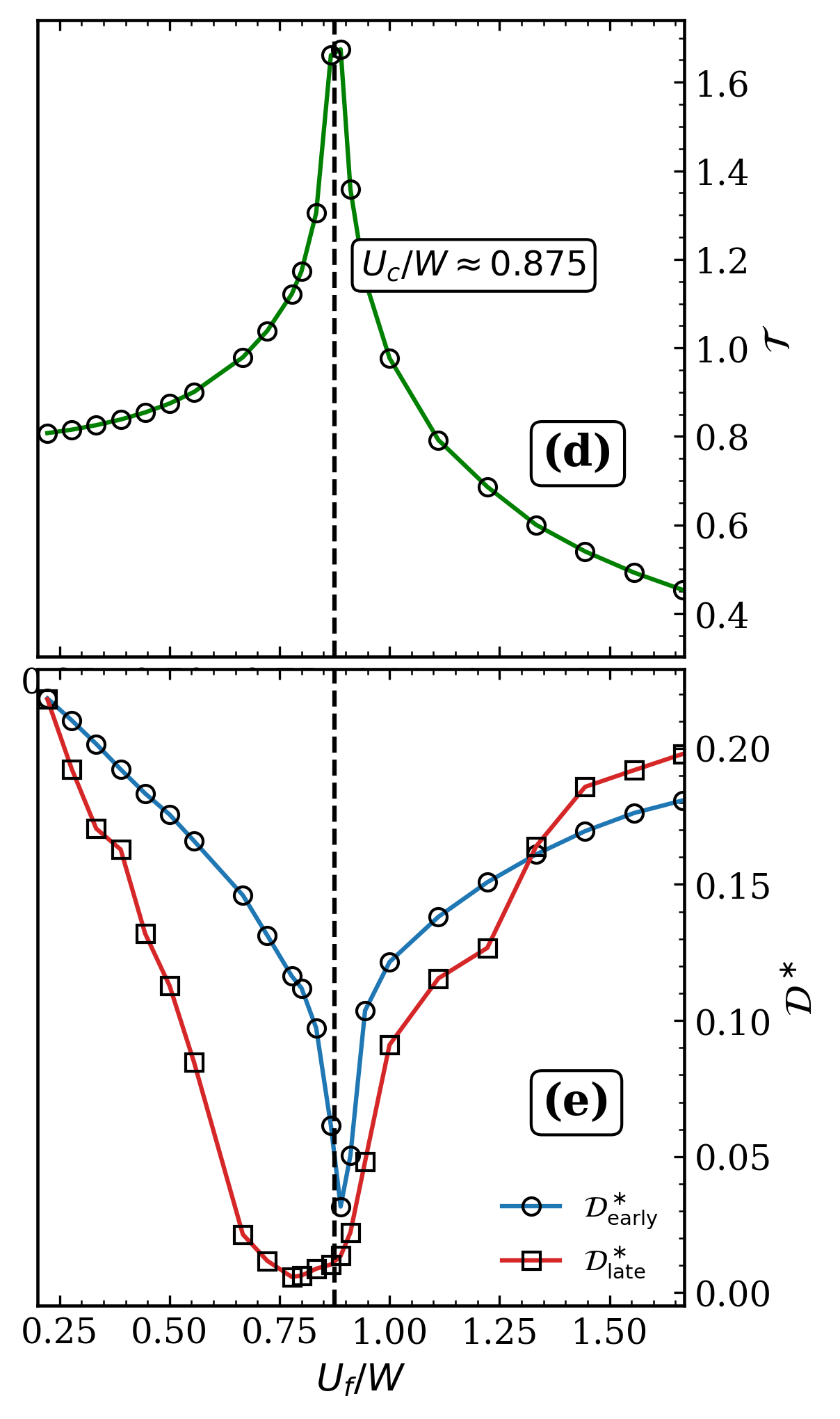
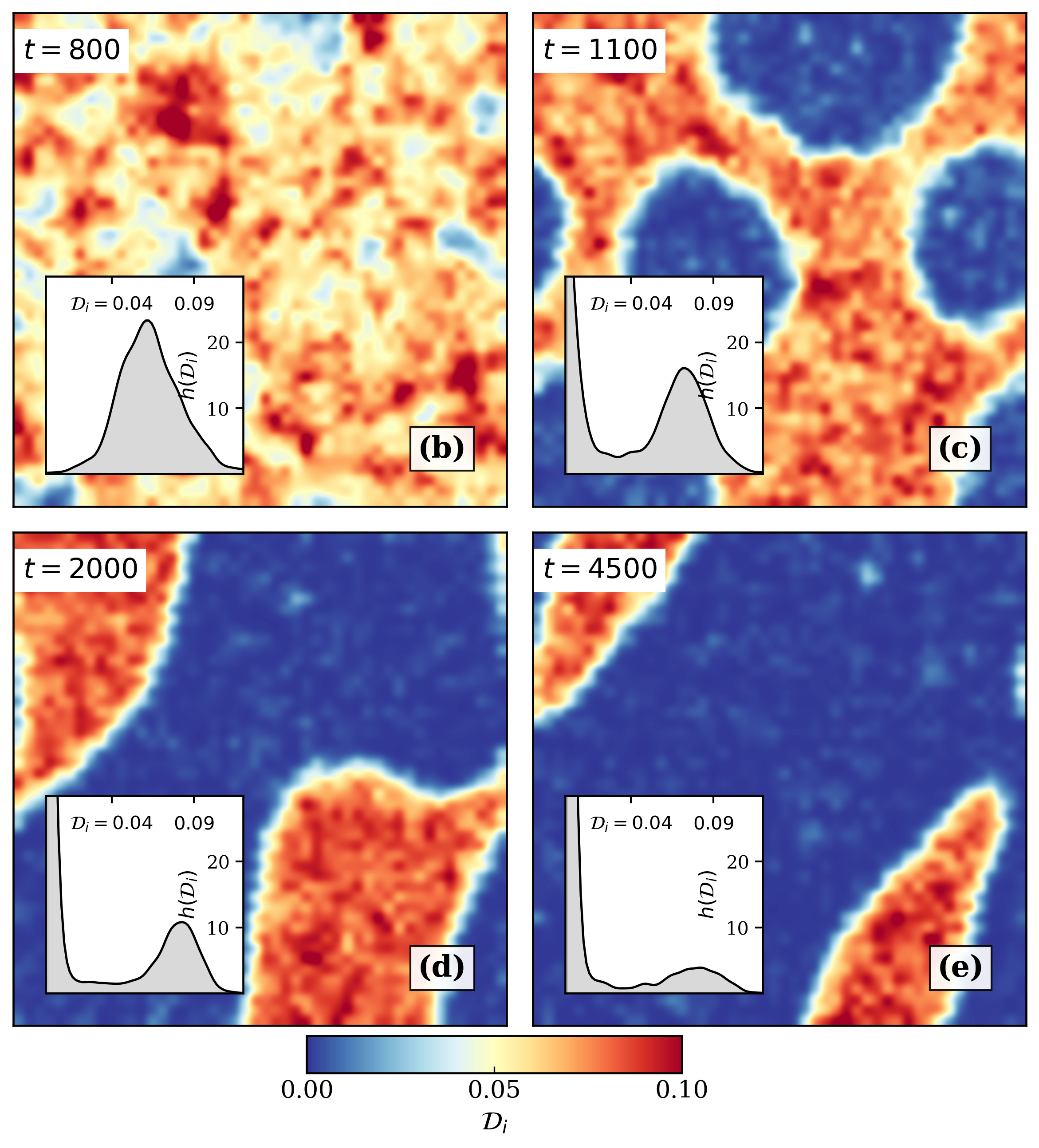
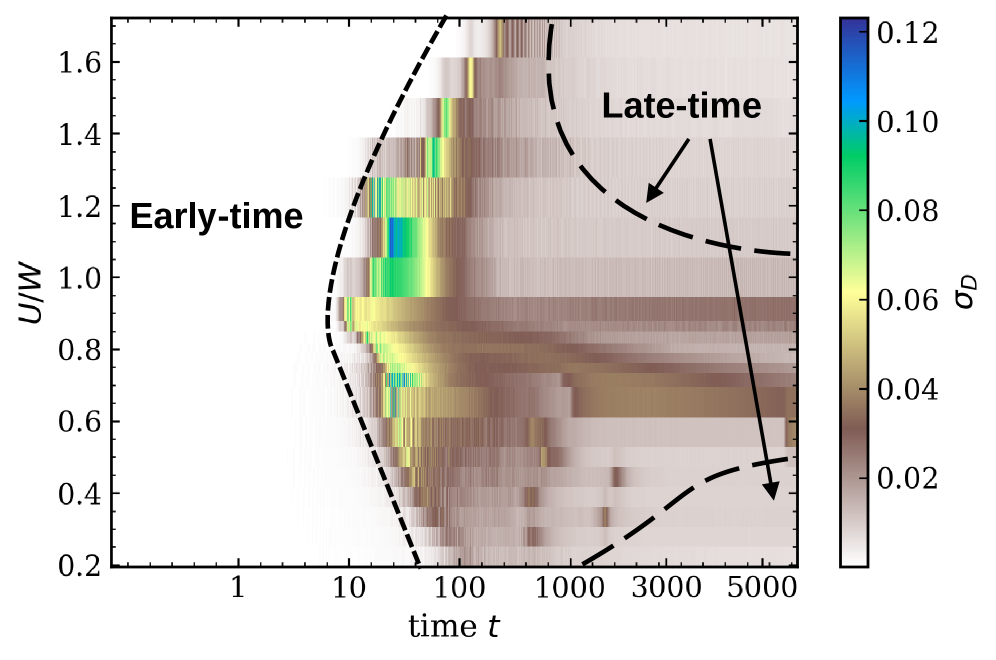
Результаты моделирования демонстрируют формирование областей, подобных моттовским изоляторам ( $Mott-like Regions$ ), и связанное с этим пространственное декогерентное поведение ( $Spatial Dephasing$ ) вследствие резкого изменения параметров системы (quench). Основным достижением является наблюдение за процессами нуклеации и медленного крупнокристаллического роста этих областей, что позволяет исследовать динамику перехода от металлического к изолирующему состоянию в пространственном разрешении. Наблюдаемая скорость коалесценции моттовских областей зависит от параметров quench и играет ключевую роль в определении конечного состояния системы.

Пространственные флуктуации двойной занятости <span class="katex-eq" data-katex-display="false"> \sigma\_{\mathcal{D}}(t) </span> зависят от времени <span class="katex-eq" data-katex-display="false"> t </span> и силы взаимодействия <span class="katex-eq" data-katex-display="false"> U_f/W </span>, при этом пунктирные линии обозначают границы между однородными режимами на ранних стадиях и неоднородным режимом на промежуточных стадиях. — Пространственные флуктуации двойной занятости $\sigma\_{\mathcal{D}}(t)$ зависят от времени $t$ и силы взаимодействия $U_f/W$ , при этом пунктирные линии обозначают границы между однородными режимами на ранних стадиях и неоднородным режимом на промежуточных стадиях.

Влияние решетки и беспорядка: Уточнение модели

Геометрия кристаллической решетки, в частности, треугольная решетка, оказывает фундаментальное влияние на динамику системы после резкого изменения параметров. Исследования показывают, что расположение атомов и их взаимосвязи в пространстве определяют характер эволюции квантовых состояний. Влияние решетки проявляется в формировании коллективных возбуждений и специфических корреляций между частицами, что напрямую сказывается на скорости и характере релаксации системы к равновесию. Различные типы решеток приводят к качественно различным динамическим режимам, демонстрируя, что топология кристаллической структуры является ключевым фактором, определяющим поведение квантовой системы после воздействия внешнего импульса. Таким образом, учет геометрии решетки необходим для адекватного описания и прогнозирования динамических свойств конденсированных сред.

Введение слабого, локализованного $Anderson$ беспорядка значительно усложняет динамику системы, вызывая появление пространственных флуктуаций. Данный тип беспорядка, проявляющийся в виде случайных отклонений потенциала в каждой точке решетки, нарушает однородность среды и приводит к локализации волновых функций. В результате, частицы испытывают различные потенциальные барьеры и ямы, что препятствует их свободному движению и приводит к возникновению неравновесных состояний. Эти флуктуации оказывают существенное влияние на когерентность и спектральные характеристики системы, внося дополнительные сложности в анализ её динамического поведения и требуя более детального исследования механизмов релаксации и переноса энергии.

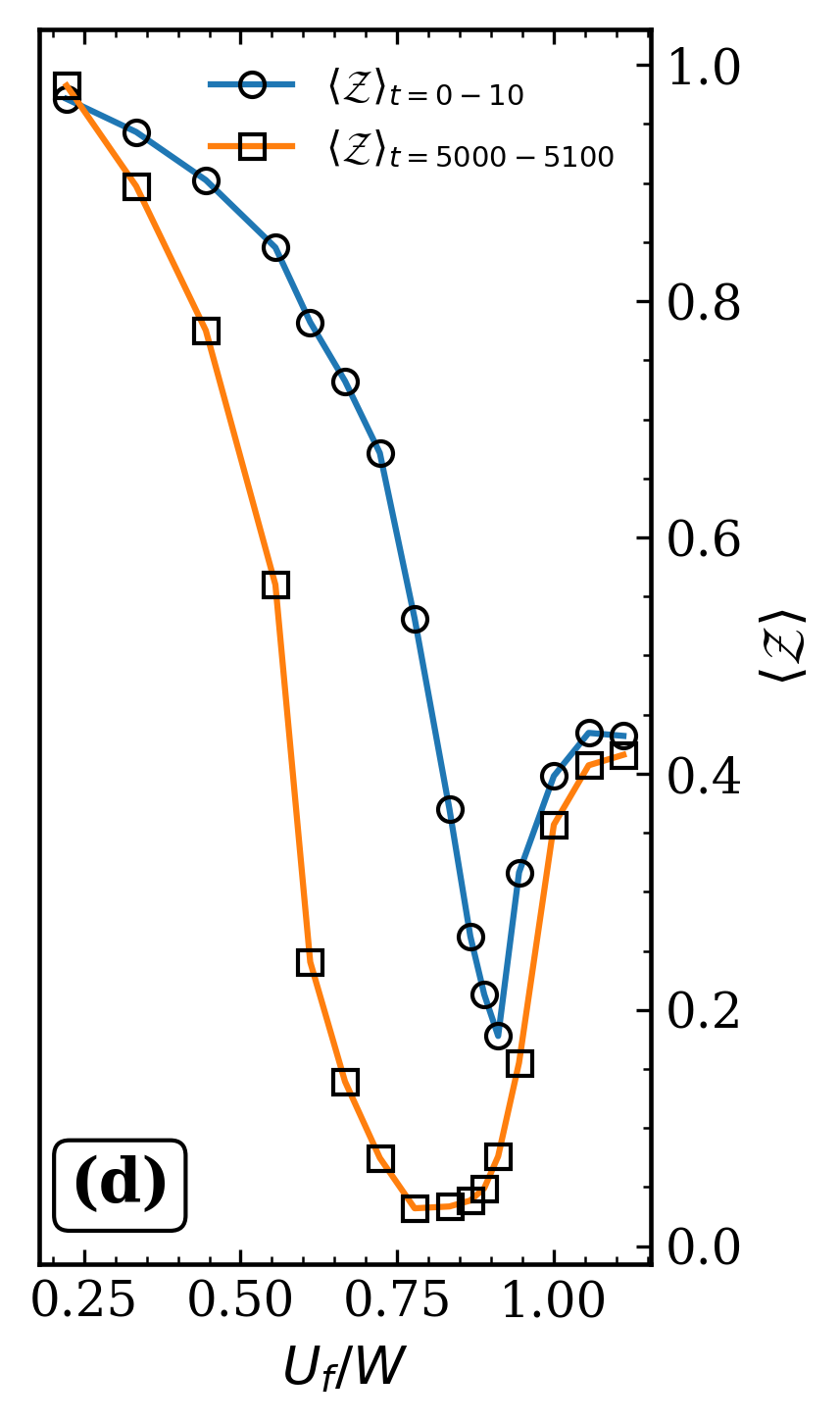
Влияние кристаллической решетки и вносимого беспорядка существенно сказывается на спектральном весе и общей когерентности системы. Наблюдаемые отклонения динамического спектрального веса $𝒵(t)$ от предсказаний однородной динамической теории среднего поля (TDGA) свидетельствуют о том, что геометрия решетки и локальные флуктуации, вызванные беспорядком, оказывают заметное влияние на эволюцию системы во времени. Эти отклонения подчеркивают важность учета микроскопических деталей структуры и неоднородностей при моделировании динамических свойств, поскольку они определяют распределение энергии и сохранение когерентности в системе, что, в свою очередь, влияет на ее общие характеристики и поведение.

Исследования показали, что скорость релаксации системы существенно зависит от ее размера. При размерах, не превышающих 30 единиц (L < 30), наблюдается ускоренное затухание, что указывает на более быструю стабилизацию системы. Однако, при увеличении размера до 30 единиц и более (L ≥ 30), зависимость двойной занятости $𝒟(t)$ от времени становится незначительной. Это свидетельствует о снижении влияния конечных размеров системы на ее динамику и указывает на то, что для достаточно больших систем результаты моделирования приближаются к пределам, соответствующим бесконечно большим системам. Таким образом, для получения достоверных результатов моделирования необходимо учитывать размер системы и использовать достаточно большие размеры, чтобы минимизировать погрешности, связанные с конечными размерами.

Figure 5:Probability distributions of the local double occupancy𝒟i(t)\mathcal{D}\_{i}(t)constructed from all sites of a48×4848\times 48lattice and averaged over the time windowt∈[1000,1100]t\in[1000,1100]. Panels (a)-(c) correspond to quenches in the weak-, intermediate-, and strong-coupling regimes, respectively.

Исследование демонстрирует, что неравновесная динамика сильно коррелированных электронных систем, особенно после квантового тушения, существенно зависит от пространственных неоднородностей. Этот аспект выходит за рамки традиционных, пространственно-однородных теоретических подходов. Подобно тому, как в биологических системах локальные взаимодействия определяют глобальное поведение, здесь пространственные флуктуации формируют эволюцию системы. Как однажды заметил Альберт Эйнштейн: «Воображение важнее знания«. Данная работа подтверждает эту мысль, показывая, что понимание сложных закономерностей требует не только знания фундаментальных принципов, но и способности представлять сложные взаимодействия, особенно в контексте неравновесной динамики, где пространственные неоднородности играют ключевую роль.

Что дальше?

Представленная работа, демонстрируя важность пространственной неоднородности в динамике сильно коррелированных электронных систем после квантового тушения, лишь приоткрывает завесу над сложной картиной неравновесных явлений. Несмотря на успехи, достигнутые с помощью приближения зависимого от времени Гуцвиллера (Time-Dependent Gutzwiller Approximation), необходимо признать, что адекватное описание взаимодействующих систем требует разработки методов, способных учитывать более сложные корреляции и топологические особенности. Очевидным направлением является развитие численных подходов, позволяющих решать уравнения динамической теории среднего поля (DMFT) в более широком классе пространственных конфигураций.

Крайне важно переосмыслить само понятие «равновесия» в контексте неравновесных систем. Поиск стационарных состояний, к которым стремится система после тушения, может оказаться бесплодным. Более продуктивным представляется исследование динамических траекторий, характеризующих эволюцию системы во времени, и выявление универсальных закономерностей, определяющих её поведение. В частности, интерес представляет вопрос о роли флуктуаций и диссипации в формировании пространственных текстур, наблюдаемых в модели Хаббарда.

Наконец, представляется важным расширить круг исследуемых моделей и систем. Переход от простой модели Хаббарда к более реалистичным описаниям материалов с сильными электронными корреляциями, учитывающим спин-орбитальное взаимодействие, кристаллическую структуру и внешние поля, может привести к обнаружению новых, неожиданных явлений. Истина, как всегда, скрыта в деталях, и её постижение требует неустанного поиска и критического анализа.

Оригинал статьи: https://arxiv.org/pdf/2601.22053.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-31 15:48