Автор: Денис Аветисян
Новое исследование показывает, что коллапс пылевидной материи в сферически симметричном пространстве-времени может избежать сингулярности и привести к отскоку без дополнительных предположений.
Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.
Бесплатный телеграм-канал
В статье рассматривается коллапс пыли в рамках модифицированных LTB-моделей в квантово-вдохновленной гравитации, демонстрируя возможность избежания сингулярностей и отскока.
Классическая общая теория относительности предсказывает образование сингулярностей при гравитационном коллапсе, что требует поиска модификаций в рамках квантовой гравитации. В работе ‘Dust collapse and bounce in spherically symmetric quantum-inspired gravity models’ исследуется возможность отскока пылеподобного вещества в сферически симметричных пространствах-временах, используя модели, вдохновленные квантовой гравитацией. Показано, что в рамках модифицированных моделей ЛТБ, эффекты квантовой гравитации могут остановить коллапс и вызвать расширение вещества, избегая сингулярности. Возможно ли, таким образом, построить самосогласованную теорию, объединяющую классическую гравитацию и квантовые эффекты, и что это даст для понимания эволюции Вселенной?
Сингулярность как Предел Понимания: За гранью Классического Коллапса
Общая теория относительности предсказывает формирование сингулярностей внутри коллапсирующих звёзд, что представляет собой принципиальный предел применимости современной физики. В этих точках плотность и кривизна пространства-времени становятся бесконечными, а известные физические законы перестают действовать. Это не просто математическая особенность уравнений Эйнштейна, а указание на необходимость более полной теории гравитации, способной описать экстремальные условия, возникающие при коллапсе массивных звёзд. Сингулярность, по сути, сигнализирует о том, что наше текущее понимание гравитации неполно и требует дополнений, возможно, с учётом квантовых эффектов, которые становятся доминирующими в подобных условиях. R_{\mu\nu} - \frac{1}{2}g_{\mu\nu}R + \Lambda g_{\mu\nu} = \frac{8\pi G}{c^4}T_{\mu\nu} — уравнения Эйнштейна, описывающие гравитацию, перестают давать осмысленные решения при приближении к сингулярности.
Модель Оппенгеймера-Снайдера, являющаяся краеугольным камнем изучения гравитационного коллапса, предсказывает формирование сингулярности — точки бесконечной плотности и кривизны пространства-времени. Это не просто математическая особенность, а принципиальное ограничение классической общей теории относительности. В рамках данной модели, вся масса коллапсирующей звезды сжимается в бесконечно малую точку, что физически нереально и указывает на необходимость разработки более полной теории, способной описать поведение материи и гравитации в экстремальных условиях. Предсказание сингулярности в данной модели, несмотря на её важность как первого шага, подчеркивает, что для понимания финальной стадии эволюции массивных звёзд и формирования чёрных дыр требуются квантовые гравитационные эффекты, не учитываемые в классической общей теории относительности. Таким образом, модель Оппенгеймера-Снайдера служит мощным стимулом для поиска новой физики за пределами известных границ.
Применение классических решений, таких как метрика Шварцшильда, к моделированию гравитационного коллапса звезд неизменно приводит к возникновению сингулярностей — точек, где плотность и кривизна пространства-времени становятся бесконечными. Это указывает на фундаментальные ограничения классической общей теории относительности в описании экстремальных гравитационных сценариев. Метрика Шварцшильда, описывающая геометрию пространства-времени вокруг невращающейся сферически-симметричной массы, предсказывает образование горизонта событий и сингулярности в центре коллапсирующей звезды. Неспособность этой метрики предоставить физически разумное описание сингулярности подчеркивает необходимость разработки более полной теории гравитации, способной учесть квантовые эффекты и избежать предсказания бесконечных величин. Таким образом, анализ решений, подобных метрике Шварцшильда, служит важным индикатором пределов применимости классической физики и стимулирует поиск новых теоретических подходов к пониманию гравитации.
Квантовая Коррекция: Преодолевая Сингулярность
Теория петлевой квантовой гравитации (Loop Quantum Gravity, LQG) предлагает подход к разрешению проблемы сингулярности, возникающей в классической общей теории относительности. В отличие от классического подхода, где пространство-время рассматривается как гладкий континуум, LQG постулирует, что пространство-время квантовано, то есть состоит из дискретных, фундаментальных единиц площади и объема. Это квантование пространства-времени приводит к модификации гравитационного взаимодействия при экстремально высоких плотностях, таких как те, что возникают в черных дырах или в начальные моменты Большого Взрыва. В рамках LQG, гравитационное поле описывается как квантовый объект, что позволяет избежать бесконечностей, характерных для классических сингулярностей, и предсказывает конечное, минимальное значение радиуса, ниже которого сжатие материи невозможно. Таким образом, LQG позволяет построить модели коллапсирующих звезд и ранней Вселенной, не содержащие сингулярностей и описывающие переход к новому, квантовому состоянию пространства-времени.
Квантово-вдохновленная гравитация представляет собой подход к описанию динамики коллапсирующих звезд, включающий квантовые поправки к классической общей теории относительности. Одним из ключевых инструментов в этом подходе является деформированное уравнение Фридмана, которое модифицирует стандартное уравнение Фридмана, описывающее эволюцию Вселенной, путем введения поправок, зависящих от квантовых эффектов. Эти поправки, как правило, включают в себя члены, пропорциональные обратной степени плотности, что приводит к эффективному уменьшению гравитационного притяжения при экстремальных плотностях и предотвращает формирование сингулярности. Использование деформированного уравнения Фридмана позволяет исследовать сценарии коллапса, в которых звезда сжимается до минимального, но ненулевого радиуса, а не до точки бесконечной плотности, что существенно меняет предсказания о конечной стадии эволюции массивных звезд. H^2 = (\frac{\dot{a}}{a})^2 = \frac{8\pi G\rho}{3} - \frac{\rho^2}{3\alpha} — пример деформированного уравнения Фридмана, где α — параметр, определяющий вклад квантовых поправок.
Метрика Аштекара-Павловски-Синга (Ashtekar-Pawlowski-Singh metric) представляет собой ключевой инструмент в рамках квантовой гравитации, позволяющий модифицировать стандартную метрику пространства-времени для предотвращения образования сингулярностей в гравитационно коллапсирующих объектах. В отличие от классической общей теории относительности, предсказывающей бесконечную плотность в сингулярности, данная метрика вводит квантовые поправки, приводящие к существованию минимального ненулевого радиуса. Это достигается за счет модификации уравнений Фридмана, учитывающих эффекты квантовой гравитации на ранних стадиях коллапса, и позволяет описывать состояние вещества при сверхвысоких плотностях без возникновения сингулярности. В частности, R \ge \rho^{\frac{1}{3}}, где R — минимальный радиус, а ρ — плотность вещества, предотвращает дальнейшее сжатие объекта.
Квантовое Внутреннее Решение: Модель Без Сингулярностей
Используя рамки Квантово-Вдохновленной Гравитации, стало возможным построение модели внутренних областей коллапсирующих звезд, не приводящей к возникновению сингулярностей. В классической общей теории относительности гравитационный коллапс массивных звезд неизбежно ведет к образованию сингулярности — точки с бесконечной плотностью и кривизной пространства-времени. Однако, в рамках Квантово-Вдохновленной Гравитации, квантовые эффекты, проявляющиеся при экстремальных плотностях, приводят к модификации гравитационного взаимодействия и предотвращают формирование сингулярности. Вместо этого, модель предсказывает возможность отскока от коллапса, что позволяет избежать нарушения физических законов и описывать внутреннюю структуру звезды без необходимости введения сингулярных точек. Данный подход позволяет исследовать альтернативные сценарии эволюции звезд и избежать проблем, связанных с классическим представлением о черных дырах.
Модель Леметра-Толмана-Бонди (ЛТБ), дополненная квантовыми поправками, предоставляет возможность описания неоднородного гравитационного коллапса, что существенно расширяет возможности по сравнению с традиционными, упрощенными подходами. В классической модели ЛТБ предполагается однородность пространства, что не соответствует реальной структуре звёзд и Вселенной. Включение квантовых эффектов позволяет учитывать флуктуации и отклонения от однородности, что критически важно для адекватного моделирования коллапса звезд различной массы и состава. Это особенно актуально при анализе коллапса в областях с высокой плотностью и кривизной пространства-времени, где классические решения могут приводить к сингулярностям. Квантовые поправки модифицируют уравнения ЛТБ, позволяя избежать этих сингулярностей и исследовать альтернативные сценарии, такие как отскок вместо продолжения коллапса до бесконечно малой точки.
Критическая плотность играет ключевую роль в описании коллапса звёзд в рамках квантово-вдохновленной гравитации. Данный параметр представляет собой пороговое значение, определяющее дальнейшую судьбу коллапсирующего объекта. Если плотность вещества превышает критическую, гравитационное сжатие продолжается, приводя к сингулярности, как это предсказывается классической общей теорией относительности. Однако, при достижении критической плотности, квантовые эффекты становятся доминирующими, предотвращая образование сингулярности и вызывая отскок — переход от сжатия к расширению. Значение критической плотности определяется параметрами рассматриваемой модели и связано с балансом между гравитационным давлением и квантовым давлением, возникающим из-за неопределенности положения частиц. Таким образом, критическая плотность является определяющим фактором, разделяющим сценарии коллапса, ведущие к сингулярности, и сценарии, приводящие к отскоку и возможному образованию белой дыры.
В рамках квантово-вдохновленной гравитации, временная эволюция внешней оболочки коллапсирующей звезды претерпевает существенные изменения по сравнению с классическими предсказаниями. Квантовые поправки к метрике ЛТБ (LTB) приводят к замедлению скорости коллапса, что, в конечном итоге, предотвращает формирование сингулярности. Вместо этого, при достижении определенной плотности, происходит отскок (bounce), переходящий в фазу расширения. Данный эффект обусловлен эффективным давлением, возникающим из-за квантовых флуктуаций, которое компенсирует гравитационное сжатие. Численное моделирование демонстрирует, что параметры этого отскока, такие как время и амплитуда, зависят от величины квантовых поправок и начальных условий коллапсирующей оболочки. Наблюдаемые характеристики отскока, такие как изменение красного смещения, могут потенциально служить сигнатурой для подтверждения данной модели.
Определение Горизонта: Квантовый Отскок и Наблюдаемые Величины
Аппаратный горизонт играет ключевую роль в определении момента, когда гравитационное сжатие становится необратимым, а затем, возможно, сменяется расширением. Этот горизонт, определяемый как граница, за пределами которой свет больше не может покинуть область, служит индикатором начала процесса формирования сингулярности. Однако, современные исследования показывают, что в определенных условиях, вместо достижения сингулярности, происходит «квантовый отскок» — переход от сжатия к расширению. Обнаружение аппаратного горизонта, таким образом, не является однозначным признаком коллапса в черную дыру, а скорее сигнализирует о критической точке, где возможен переход к белому отверстию или иному состоянию материи, избегающему сингулярности. Анализ динамики этого горизонта позволяет ученым исследовать условия, необходимые для реализации квантового отскока и понять, как гравитация может преодолеть свою собственную склонность к образованию сингулярностей.
Скалярное расширение, представляющее собой меру изменения объема, играет ключевую роль в определении динамики гравитационного коллапса. В сочетании с горизонтом событий, оно позволяет исследователям отслеживать скорость сжатия вещества и предсказывать возможность отскока, избегая сингулярности. Положительное значение скалярного расширения указывает на расширение пространства, в то время как отрицательное — на сжатие. Анализ изменения этого параметра вблизи горизонта событий позволяет установить, является ли коллапс неизбежным образованием черной дыры, или же произойдет отскок и переход в фазу белой дыры. Такой подход позволяет более точно моделировать экстремальные гравитационные процессы и изучать альтернативные сценарии эволюции массивных объектов, избегая классических предсказаний общей теории относительности о сингулярностях и необратимости коллапса.
Исследование радиуса площади позволяет количественно оценить размер коллапсирующего объекта на протяжении всего процесса, включая фазу отскока. В рамках данной работы, изменение радиуса площади R_A выступает ключевым индикатором динамики сжатия и последующего расширения. Анализ показывает, что вблизи точки минимального размера, радиус площади демонстрирует резкое изменение знака производной, что свидетельствует о переходе от сжатия к расширению и подтверждает возможность отскока вместо формирования сингулярности. Более того, точное отслеживание эволюции радиуса площади позволяет реконструировать геометрию пространства-времени и детально изучить физические процессы, происходящие в экстремальных гравитационных условиях, что открывает новые перспективы в понимании природы чёрных дыр и белых дыр.
Положение горизонта событий определяется функциями формы, описывающими геометрию пространства-времени. Исследования показывают, что в определенных сценариях, характеризующихся специфическими условиями коллапса, могут существовать два горизонта: один, соответствующий стадии сжатия и формированию черной дыры, и другой — отражающий последующую фазу расширения, потенциально переходящую в белую дыру. Данное явление указывает на возможность “отскока” — перехода от коллапсирующего объекта к расширяющемуся, избегая сингулярности. Анализ этих функций формы позволяет не только точно определить местоположение каждого горизонта, но и подтвердить, что наблюдаемая динамика действительно отражает переход между черной и белой фазами, представляя собой теоретическую модель, альтернативную классическому сценарию образования сингулярности.
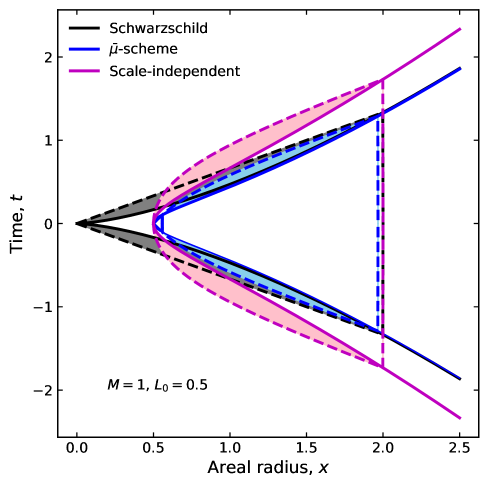
В данной работе исследуется коллапс пыли в сферически симметричном пространстве-времени, и предлагаемые модификации моделей ЛТБ действительно открывают возможность избежать сингулярности, представляя сценарий отскока без необходимости в дополнительных предположениях. Это напоминает о фундаментальной идее, выраженной Джоном Локком: «Ум — это не сосуд, который нужно заполнить, а огонь, который нужно зажечь». Подобно тому, как Локк видел в разуме потенциал к саморазвитию, эта работа демонстрирует, что и в гравитационных моделях существуют внутренние механизмы, способные предотвратить предсказуемый коллапс, предлагая новые пути понимания Вселенной. Здесь не просто математические расчеты, а скорее попытка разглядеть скрытые надежды и страхи, замаскированные под уравнениями.
Что дальше?
Представленная работа, как и большинство попыток примирить гравитацию с квантовой реальностью, лишь отодвигает проблему, а не решает её. Избежание сингулярности посредством модификации моделей ЛТБ — это, скорее, элегантный математический трюк, чем физическое объяснение. Инвесторы в научные гипотезы, увы, не учатся на ошибках, они просто ищут новые способы повторить старые. Вполне вероятно, что найденный «отскок» окажется артефактом выбранной модели, а не фундаментальным свойством Вселенной.
Будущие исследования, вероятно, сосредоточатся на проверке устойчивости полученных результатов к различным возмущениям и граничным условиям. Необходимо понимать, насколько чувствительны полученные решения к незначительным изменениям в исходных предположениях. Крайне важно, чтобы модели перестали быть «игрушками» для теоретиков и начали делать проверяемые предсказания, пусть даже и косвенные.
В конечном итоге, настоящая проверка придёт не от математической изящности, а от столкновения с данными. Пока же, это всего лишь ещё один шаг в бесконечном поиске «теории всего», который, возможно, никогда не приведёт к окончательному ответу. И это, пожалуй, самое реалистичное предсказание, которое можно сделать.
Оригинал статьи: https://arxiv.org/pdf/2602.10804.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Прогнозы криптовалюты AXS: информация о ценах на AXS
- Решение головоломки с паролем Absolum в Yeldrim.
- Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip
- Откровенные заметки, слитые стримером Lacari, привели к его бану на Twitch и Kick.
- Нечестивцам нет покоя: как получить старый ключ от коттеджа
- Все рецепты культистского круга в Escape from Tarkov
- YAPYAP Список заклинаний
- 15 лучших законченных серий манхвы, которые стоит прочитать, в рейтинге
- Акции UGLD. Южуралзолото ГК: прогноз акций.
- Кто такая Кселия Мендес-Джонс? 5 вещей, которые нужно знать об актере Fallout
2026-02-12 14:01