Распространение квантовой магии: как рождается вычислительная мощность

Автор: Денис Аветисян

Новое исследование показывает, как квантовые ресурсы, необходимые для сложных вычислений, распространяются в квантовых системах под воздействием определенных динамических процессов.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал

В рамках исследования динамики роста запутанности и распространения операторов в случайных квантовых схемах, установлено, что скорость роста «магии» — меры отклонения от классического поведения — ограничена верхней границей, предсказанной уравнением $S10$, причём для систем с открытыми и периодическими граничными условиями наблюдается согласованный рост $W(t)$, соответствующий скорости бабочки $v_B$, удвоенной скорости запутанности $2v_E$ и максимальной скорости $v^{\max}_W = v_B + 2v_E$, что подтверждается усреднением по $10^{2}$ реализациям схем с использованием случайных стабилизационных состояний и архитектуры, представленной в рисунке S2 для $L=50$.

Работа посвящена изучению распространения ‘магических’ состояний в контексте квантовой коррекции ошибок и единичной Клиффорд-динамики, устанавливая границы скорости распространения квантовых ресурсов.

Несмотря на важность квантовой немагичности как ресурса для коррекции ошибок и вычислений, ее локальное распределение и динамика остаются плохо изученными из-за отсутствия напрямую измеримых наблюдаемых. В работе «Magic spreading under unitary Clifford dynamics» исследуется распространение квантовой немагичности в цепях Клиффорда, демонстрируя, что ее динамика определяется ростом запутанности и скоростью распространения операторов. Разработанный подход, основанный на кодах коррекции ошибок, позволяет выводить пространственное распределение немагичности и определить характерные масштабы ее локализации. Какие новые перспективы открываются для понимания транспорта квантовых ресурсов и их связи с квантовой коррекцией ошибок в более сложных системах?

Пределы Стабилизированных Вычислений

Универсальные квантовые вычисления, в отличие от классических, требуют не только запутанности — фундаментального ресурса, лежащего в основе многих квантовых протоколов, но и так называемых “магических состояний”. Эти состояния, не стабилизируемые никакими кодами коррекции ошибок, представляют собой необходимый компонент для реализации произвольных квантовых операций. Без них квантовый компьютер, даже обладающий большим количеством кубитов и эффективной коррекцией ошибок, оказывается неспособен выйти за рамки ограниченного набора вычислений, эквивалентных классическим алгоритмам. В сущности, “магические состояния” позволяют преодолеть ограничения, накладываемые стабилизированными кодами, и открывают путь к полной универсальности квантовых вычислений, требуя, однако, новых подходов к их генерации, хранению и манипулированию. Их роль аналогична добавлению нелинейности в линейную систему — без них невозможно реализовать все желаемые преобразования.

Традиционные методы квантовой коррекции ошибок, основанные на кодах стабилизаторов, сталкиваются с существенными трудностями при эффективной реализации операций над так называемыми «магическими состояниями». Эти состояния, необходимые для универсальных квантовых вычислений, не могут быть защищены стандартными кодами стабилизаторов, поскольку операции, необходимые для их создания и манипулирования, разрушают свойства, обеспечивающие коррекцию ошибок. Попытки реализации таких операций требуют значительно больших ресурсов, чем операции, защищенные кодами стабилизаторов, что создает узкое место в масштабировании отказоустойчивых квантовых компьютеров. Проблема заключается в том, что $T$-вентили, необходимые для создания универсального набора квантовых операций, не могут быть надежно реализованы в рамках исключительно стабилизаторных схем, что ограничивает возможности практического применения существующих методов коррекции ошибок и стимулирует поиск альтернативных подходов.

Ограничения, накладываемые традиционными методами коррекции ошибок, препятствуют масштабированию отказоустойчивых квантовых компьютеров. Суть проблемы заключается в неэффективности работы со «магическими состояниями» — ресурсами, необходимыми для универсальных квантовых вычислений, выходящими за рамки простой запутанности. Невозможность эффективно манипулировать и распространять эти состояния становится критическим узким местом, ограничивающим возможности создания действительно мощных квантовых вычислительных систем. В связи с этим, активно ведутся исследования, направленные на разработку новых подходов к управлению «магией», что является ключевым шагом на пути к реализации практичных и масштабируемых квантовых технологий. Успех в этой области позволит преодолеть существующие ограничения и открыть новые горизонты в квантовых вычислениях.

Процедура позволяет извлечь единицу магии из чистого состояния |ψ⟩ путем концентрирования магии в подсистеме AA и применения клиффордского преобразования, что позволяет дистиллировать магическое состояние |T⟩ в системе CC, изначально находящейся в стабилизированном состоянии.

Характеризуя Магию: За Пределами Запутанности

Явление, обозначаемое как “магия” в контексте квантовых ресурсов, неразрывно связано с не-гауссовостью — фундаментальным квантовым свойством, характеризующим отклонение от классических корреляций. Гауссовы состояния описывают системы, поведение которых предсказуемо на основе классической статистики, в то время как не-гауссовые состояния демонстрируют квантовые эффекты, недоступные в классической физике. Таким образом, наличие “магии” подразумевает присутствие не-гауссовости, что делает последний показатель необходимым критерием для идентификации и оценки квантовых ресурсов, превосходящих возможности классических систем. Измерение степени не-гауссовости позволяет количественно оценить “магию”, определяя потенциал квантовой системы для выполнения задач, невозможных для классических аналогов.

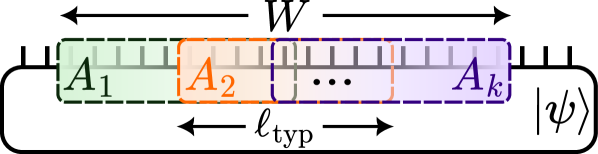
Пространственное распространение “магии” в квантовых системах может быть количественно оценено с помощью понятия “линейной магической длины”. Данная величина представляет собой меру влияния неклассических корреляций на состояние системы, определяя область пространства, в которой проявляются эффекты, невозможные в классической физике. Линейная магическая длина рассчитывается на основе анализа корреляционных функций и позволяет установить связь между локальными свойствами квантового состояния и его глобальным влиянием. В отличие от простого определения наличия или отсутствия “магии”, эта метрика предоставляет возможность сравнить различные квантовые состояния по степени их неклассичности и оценить эффективность использования “магических” ресурсов в квантовых технологиях. Значение $L$ линейной магической длины, как правило, зависит от геометрии системы и конкретного типа неклассических корреляций.

Энтропия Реньи является важным инструментом для характеризации запутанности, сопутствующей «магии» — неклассическому квантовому ресурсу. В отличие от стандартной энтропии фон Неймана, энтропия Реньи позволяет более детально исследовать корреляции различного порядка в квантовой системе. Она определяется как $S_\alpha = \frac{1}{1-\alpha} \log \text{Tr}(\rho^\alpha)$, где $\rho$ — матрица плотности, а $\alpha$ — параметр, определяющий порядок корреляций. Анализ энтропии Реньи при различных значениях $\alpha$ позволяет выявить и количественно оценить вклад различных видов запутанности в общий ресурс «магии», раскрывая взаимосвязь между этими двумя квантовыми ресурсами и предоставляя более полное понимание их природы и возможностей.

Характерная длина магии определяется размером минимальных, непересекающихся подсистем, из которых можно извлечь квантовую запутанность из состояния |ψ⟩.

Моделирование Распространения Магии и Квантового Хаоса

Самодуальная схема возбужденного изосингового спина (SDKIFCircuit) представляет собой вычислительно эффективную модель для симуляции распространения «магии» — меры квантовой запутанности и нелокальности. Данная схема, основанная на дискретном временном развитии, позволяет отслеживать эволюцию магических свойств системы во времени, избегая вычислительных сложностей, возникающих при моделировании более реалистичных, непрерывно развивающихся квантовых систем. Использование SDKIFCircuit обусловлено её способностью сохранять ключевые физические характеристики, определяющие распространение магии, при этом позволяя проводить симуляции на сравнительно небольших вычислительных ресурсах. Это делает её ценным инструментом для изучения динамики квантовой информации и хаоса в контролируемой среде.

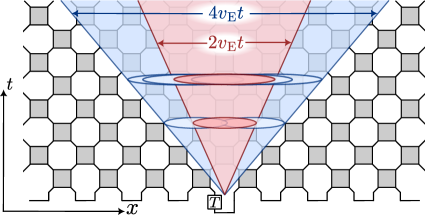
Результаты моделирования показывают, что ‘магия’ распространяется в системе, что подтверждается динамикой линейной длины магии $W(t)$. Скорость этого распространения ограничена суммой скорости ‘бабочки’ ($v_B$) и скорости запутанности ($v_E$). В частности, установлено, что линейная длина магии не может расти быстрее, чем $W(t) ≤ 2(v_Bt + 2v_Et)$. Данное неравенство определяет верхнюю границу скорости распространения магии, обусловленную физическими параметрами моделируемой системы.

Распространение «магии» в моделируемой системе тесно связано с квантическим хаосом. Скорость «бабочки» ($v_B$) характеризует скорость рассеяния информации и, как следствие, «магии» в системе. Максимальная скорость распространения «магии» ($v_{W_{max}}$) определяется как сумма скорости «бабочки» и удвоенной скорости запутанности ($v_{W_{max}} = v_B + 2v_E$). Данная зависимость указывает на фундаментальную связь между скоростью распространения информации, квантовым хаосом и динамикой «магии» в рассматриваемой модели.

В схеме с добавлением ошибок и случайными Клиффордскими гейтами, локально вводимая магия распространяется со скоростью, определяемой скоростью запутанности, ограничиваясь областью, за пределами которой невозможно уменьшить магию.

Манипулирование Магией посредством Проектирования Схем

Унитарные схемы Клиффорда представляют собой базовую платформу для моделирования квантовой динамики, однако их возможности по созданию и поддержанию “магии” — способности, превосходящей возможности классических вычислений — ограничены. Данные схемы, хотя и эффективны для определенных задач, склонны к быстрому распаду квантовых состояний, что препятствует выполнению сложных вычислений, требующих сохранения когерентности. Ограничения возникают из-за структуры самих схем, которые не позволяют эффективно генерировать и распространять запутанность, являющуюся ключевым ресурсом для квантовых алгоритмов. В результате, для достижения значительной вычислительной мощности, необходимо искать способы модификации или расширения возможностей унитарных схем Клиффорда, преодолевая их присущие ограничения в поддержании квантовой “магии”.

Исследования показали, что введение так называемых «идентичных допант» — дополнительных операций, не меняющих состояние кубитов, — в унитарные клиффорд-схемы оказывает значительное влияние на их способность генерировать и поддерживать квантовую «магию». Этот подход, заключающийся в добавлении идентичных гейтов, фактически модифицирует структуру схемы, создавая более благоприятные условия для распространения и сохранения квантовой запутанности. В результате, схемы с «идентичным допингом» демонстрируют повышенную устойчивость к декогеренции и способны выполнять более сложные квантовые вычисления, что открывает новые возможности для разработки мощных квантовых алгоритмов и расширения вычислительных возможностей.

Исследования показали, что временная шкала сжатия логических операторов, определяемая как $t^* = L/(2v_{W_{max}}) = L/(6v_E)$, представляет собой критический порог, влияющий на динамику квантовых вычислений. Данный параметр, связывающий длину логического оператора ($L$) со скоростью распространения изменений ($v_E$ или $v_{W_{max}}$), определяет момент, когда эффективность использования квантовой “магии” — способности выполнять вычисления, невозможные для классических компьютеров — существенно возрастает. Превышение этого порога позволяет более эффективно генерировать и распространять квантовые ресурсы, что, в свою очередь, приводит к улучшению вычислительной мощности и открывает возможности для решения сложных задач, недоступных современным алгоритмам. Понимание и контроль над этой временной шкалой является ключевым фактором в разработке более мощных и эффективных квантовых вычислительных систем.

Пропускная способность канала, характеризующая сохранение квантовой запутанности, остается порядка единицы при частоте кодирования до 0.5, но быстро снижается до нуля при дальнейшем увеличении частоты, что свидетельствует о потере квантовой информации.

Исследование, представленное в статье, демонстрирует, что распространение квантовой «магии» — ресурса, необходимого для вычислений, превосходящих возможности классических компьютеров — тесно связано с ростом запутанности и распространением операторов. Этот процесс, как показывает работа, имеет четкие границы, определяющие скорость распространения «магии». В связи с этим вспоминается высказывание Луи де Бройля: «Всякое явление может быть рассмотрено с двух противоположных точек зрения, в зависимости от того, что мы наблюдаем: волну или частицу». Подобно двойственности волны и частицы, и здесь распространение «магии» проявляется через различные, взаимосвязанные аспекты — запутанность и операторное распространение — и понимание этих взаимосвязей критически важно для контроля и использования этого ценного ресурса в квантовых вычислениях. Работа подчеркивает, что истинное понимание требует учета не только наблюдаемых эффектов, но и границ их проявления.

Что дальше?

Представленные результаты, хотя и проливают свет на динамику распространения «магии» в квантовых системах, лишь подчеркивают сложность адекватного описания квантовых ресурсов. Ограничения, накладываемые рассмотрением лишь унитарной динамики в рамках кодов стабилизаторов, неизбежно сужают картину. Необходимо расширить исследования за пределы этих упрощений, включив в рассмотрение более общие типы динамики и кодов, а также учитывать влияние шума и декогеренции — факторов, которые в реальных квантовых устройствах играют далеко не последнюю роль. Данные — не цель, а зеркало человеческих ошибок, и игнорировать эту очевидную истину было бы неразумно.

Особый интерес представляет вопрос о связи между распространением «магии» и более общими понятиями квантового хаоса. Установленные границы скорости распространения, безусловно, важны, но они лишь описывают один аспект проблемы. Необходимо разработать более глубокое теоретическое понимание механизмов, лежащих в основе этой динамики, и исследовать, как эти механизмы влияют на производительность квантовых вычислений. Всё, что нельзя измерить, всё равно влияет — просто это труднее моделировать.

В конечном счете, истинный прогресс потребует не только развития теоретических моделей, но и проведения экспериментов, способных проверить эти модели в реальных квантовых системах. Это потребует разработки новых методов измерения и контроля квантовых ресурсов, а также значительных усилий по преодолению технических трудностей, связанных с построением и поддержанием когерентных квантовых состояний. По сути, задача состоит не в том, чтобы «приручить» квантовую механику, а в том, чтобы научиться понимать её прихотливую логику.

Оригинал статьи: https://arxiv.org/pdf/2511.21487.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2025-11-29 19:44