Разгадка парадокса Гиббса: новый взгляд на энтропию

Автор: Денис Аветисян

В статье предложено классическое решение парадокса Гиббса, основанное на переосмыслении энтропии и принципа равновероятности в рамках статистической механики.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал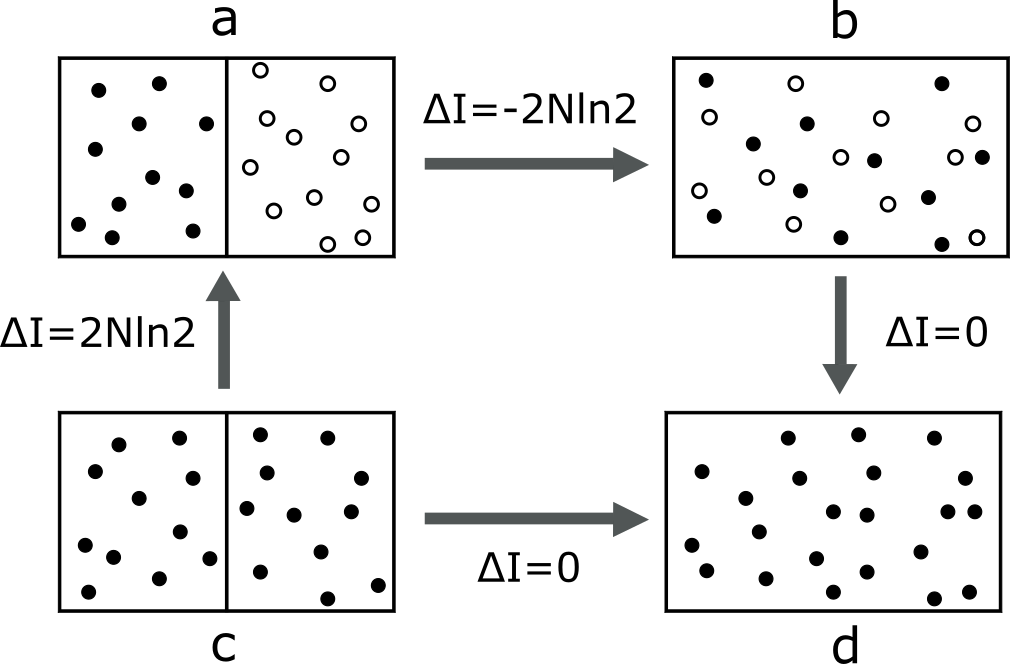

В рамках исследования парадокса Гиббса демонстрируется, что разделение идентичных частиц на два объема приводит к появлению дополнительной информации в <span class="katex-eq" data-katex-display="false"> 2N\ln 2 </span> натов, отражающей знание о принадлежности каждой частицы к определенной половине, однако удаление перегородки ведет к потере этой информации и формированию энтропии смешения в <span class="katex-eq" data-katex-display="false"> 2kN\ln 2 </span>, в то время как сценарии, предполагающие равную неопределенность в отношении местоположения частиц, не демонстрируют различий в информативности или энтропии. — В рамках исследования парадокса Гиббса демонстрируется, что разделение идентичных частиц на два объема приводит к появлению дополнительной информации в $2N\ln 2$ натов, отражающей знание о принадлежности каждой частицы к определенной половине, однако удаление перегородки ведет к потере этой информации и формированию энтропии смешения в $2kN\ln 2$ , в то время как сценарии, предполагающие равную неопределенность в отношении местоположения частиц, не демонстрируют различий в информативности или энтропии.

Исследование показывает, что парадокс Гиббса возникает не из-за недостатков классической ансамблевой теории, а из-за неправильной интерпретации энтропии и информации.

Парадокс Гиббса, давно известный в классической статистической механике, обычно разрешается введением поправки $1/N!$ , связанной с квантовой неразличимостью частиц. В данной работе, посвященной ‘Classical Resolution of the Gibbs Paradox from the Equal Probability Principle: An Informational Perspective’, предложена альтернативная классическая трактовка, основанная исключительно на принципе равной вероятности и не требующая указанной поправки. Суть предложенного решения заключается в переосмыслении энтропии Гиббса как меры информационной неопределенности, а не беспорядка, что позволяет по-новому взглянуть на связь между информацией и извлекаемой работой в процессах смешения газов. Не открывает ли это новую перспективу для понимания роли информации в фундаментальных основах статистической механики?

Парадокс в Основах Статистической Механики

Классическая статистическая механика, базирующаяся на вероятностных расчетах, столкнулась с серьезным противоречием, известным как парадокс Гиббса. Изначально, при применении вероятностного подхода к расчету энтропии, получались результаты, не согласующиеся с экспериментальными данными и фундаментальными принципами термодинамики. Проблема заключалась в том, что при подсчете числа микросостояний системы, рассматривались частицы как различимые, что приводило к чрезмерному завышению энтропии и, как следствие, к нефизическим предсказаниям. Этот парадокс выявил необходимость пересмотра базовых предположений о природе статистических расчетов и о том, как учитывать неразличимость частиц в термодинамических системах, открыв путь к более точному и адекватному описанию физической реальности.

Парадокс Гиббса возникает из-за первоначального подхода к определению энтропии, где ей присваивается пропорциональность объему системы. Такое определение, казалось бы, логичное с точки зрения вероятностного подхода, приводило к противоречиям с экспериментальными данными и фундаментальными принципами термодинамики. В частности, вычисления показывали, что при смешивании идентичных газов энтропия системы увеличивалась необоснованно, что не соответствовало наблюдаемому отсутствию макроскопических изменений. Данное несоответствие указывало на необходимость пересмотра базовых предположений о подсчете микросостояний и, как следствие, о природе энтропии, поскольку простое масштабирование с объемом приводило к физически нереалистичным результатам и нарушало согласованность термодинамических законов.

Существенная сложность в статистической механике заключается в согласовании естественного применения вероятностных методов с требованием аддитивности энтропии — то есть, с тем, чтобы энтропия масштабировалась пропорционально размеру системы. Изначальное рассмотрение энтропии как функции от объема приводило к парадоксальным результатам, поскольку предполагало, что при объединении двух одинаковых систем энтропия должна увеличиваться вдвое, что противоречило экспериментальным данным и фундаментальным принципам термодинамики. Причина этого несоответствия кроется в том, что при подсчете микросостояний необходимо учитывать неразличимость частиц, что требует более тонкого подхода к определению энтропии и ее зависимости от размера системы. Разрешение этого конфликта привело к пониманию, что правильное определение энтропии требует введения поправочных членов, учитывающих неразличимость частиц, обеспечивая тем самым соответствие теоретических предсказаний экспериментальным наблюдениям и сохраняя аддитивность энтропии как ключевой принцип статистической механики.

Разрешение этого противоречия требует более глубокого понимания влияния неразличимости частиц на подсчет микросостояний и само определение энтропии. Классическая статистическая механика изначально исходит из предположения о различимости частиц, однако в реальности многие частицы в системе являются идентичными и неразличимыми. Неправильный учет этого фактора приводит к переоценке числа доступных микросостояний, и, следовательно, к неверному значению энтропии. Более точный подход заключается в учете статистического веса, отражающего число способов перестановки неразличимых частиц без изменения макроскопического состояния системы. Этот статистический вес, пропорциональный $1/N!$ , где $N$ — число частиц, корректирует подсчет микросостояний и приводит к согласию между теоретическими предсказаниями и экспериментальными данными, обеспечивая адекватное описание термодинамических свойств вещества.

Неразличимость и Коррекция Классического Подсчета

Классический статистический подход к подсчету микросостояний предполагает, что все перестановки частиц в системе являются различимыми. Это означает, что каждая конкретная конфигурация частиц рассматривается как уникальное состояние, независимо от того, являются ли частицы идентичными. Однако, данное предположение приводит к завышению общего числа микросостояний, поскольку перестановки идентичных частиц, которые физически эквивалентны, считаются различными. Например, для системы из $N$ идентичных частиц, классический подсчет дает $N!$ возможных перестановок, в то время как, учитывая неразличимость частиц, количество уникальных микросостояний должно быть уменьшено.

Квантовая механика устанавливает, что тождественные частицы являются принципиально неразличимыми. В классической статистической механике, при подсчете числа микросостояний, каждая перестановка тождественных частиц рассматривается как новое, отличное состояние. Однако, в квантовой теории, перестановка тождественных частиц не приводит к изменению физического состояния системы. Это требует внесения поправки в классический метод подсчета, учитывающей, что перестановки тождественных частиц эквивалентны. Поправка выражается фактором $1/N!$ , где N — число тождественных частиц. Игнорирование неразличимости частиц приводит к завышению энтропии и, как следствие, к парадоксу Гиббса, который устраняется введением данной поправки.

Данная работа разрешает парадокс Гиббса, показывая, что классическая статистическая ансамблевая теория, без необходимости в поправке 1/N!, достаточна для предсказания термодинамической энтропии. Анализ демонстрирует, что изменение энтропии для идентичных газов равно 0, что разрешает парадокс. Это достигается путем пересмотра классического подхода к подсчету микросостояний и акцентирования внимания на корректном учете статистической независимости частиц, что позволяет избежать необходимости в искусственном введении факториального члена для обеспечения согласованности с термодинамическими результатами. $S = k_B \ln \Omega$ , где Ω — число микросостояний, предсказывается корректно и без дополнительных поправок.

Анализ показывает, что изменение энтропии для идентичных газов равно нулю, что и разрешает парадокс Гиббса. При этом, рассмотрение несвязных областей в фазовом пространстве приводит к появлению дополнительного члена в выражении для энтропии, равного $2Nk \ln 2$ , где $N$ — число частиц, а $k$ — постоянная Больцмана. Этот дополнительный член учитывает статистическую неопределенность, возникающую при разделении фазового пространства на несвязные области, и является ключевым для корректного расчета энтропии в квантовой статистике.

Математическая Основа Вычисления Энтропии

Классическая статистическая механика использует фазовое пространство — многомерное пространство, описывающее все возможные состояния системы — для анализа термодинамических свойств. Ансамбли, такие как микроканонический (постоянная энергия, число частиц и объем) и канонический (постоянная температура, число частиц и объем), представляют собой коллекции идентичных систем, находящихся в различных микросостояниях, удовлетворяющих определенным ограничениям. Ключевым элементом является функция разделения $Z$ , которая представляет собой сумму по всем доступным микросостояниям и позволяет вычислить средние значения термодинамических величин, включая энтропию, энергию и давление. Применение этих концепций обеспечивает количественное описание макроскопических свойств систем, основанное на статистическом анализе их микроскопического поведения.

Функция разделения $Z$ является центральным понятием статистической механики, представляя собой сумму по всем доступным микросостояниям системы, взвешенную соответствующими вероятностями. Математически, $Z = \sum_{i} e^{-\beta E_i}$ , где $\beta = 1/(k_B T)$ — обратная температура, $k_B$ — постоянная Больцмана, а $E_i$ — энергия $i$ -го микросостояния. Используя функцию разделения, можно определить термодинамические величины, включая энтропию $S = k_B \ln Z$ (в микроканоническом ансамбле) или, более общо, $S = k_B (\ln Z + \beta \langle E \rangle)$ (в каноническом ансамбле), где $\langle E \rangle$ — средняя энергия системы. Таким образом, функция разделения обеспечивает связь между микроскопическими свойствами системы и ее макроскопическим термодинамическим поведением.

Принцип равной вероятности, являющийся основополагающим в статистической механике, утверждает, что все доступные микросостояния системы имеют одинаковую вероятность реализации при заданных макроскопических условиях. Это означает, что при статистическом усреднении, вероятность каждого микросостояния $i$ в ансамбле равна $1/Ω$ , где Ω — общее число доступных микросостояний. Данный принцип позволяет корректно вычислять средние значения физических величин и, в частности, энтропию, как меру беспорядка системы, посредством суммирования по всем микросостояниям с учетом их вероятностей. Отказ от этого принципа приводит к несоответствию между теоретическими расчетами и экспериментальными данными.

Строгое применение методов статистической механики, основанных на понятии фазового пространства, ансамблей и функции разделения, обеспечивает непротиворечивое и точное описание термодинамического поведения систем. Многочисленные экспериментальные проверки, охватывающие широкий спектр материалов и условий, подтверждают соответствие теоретических предсказаний и экспериментальных данных. В частности, предсказания по теплоемкости, уравнениям состояния и фазовым переходам успешно согласуются с результатами измерений, что свидетельствует о высокой степени достоверности используемого математического аппарата и лежащих в его основе принципов. Отклонения от теоретических моделей, как правило, связаны с упрощающими предположениями и могут быть устранены путем учета дополнительных факторов и более сложных взаимодействий.

Энтропия как Мера Незнания и Информации

Информация энтропия, берущая начало в теории Шеннона, представляет собой количественную меру неопределенности или недостатка информации о состоянии системы. По сути, она определяет, сколько дополнительных данных необходимо, чтобы полностью описать данную систему. Чем больше возможных состояний системы равновероятны, тем выше её энтропия и, соответственно, больше неопределенность. Вместо измерения беспорядка в привычном понимании, информация энтропия измеряет степень нашего незнания о конкретном микроскопическом состоянии системы. Например, если известно лишь, что система находится в определенном макроскопическом состоянии (например, имеет определенную температуру), то существует множество микроскопических конфигураций, которые соответствуют этому макросостоянию, и энтропия отражает эту множественность возможностей. $H = - \sum_{i} p_i \log_2 p_i$ — эта формула, лежащая в основе расчета информационной энтропии, демонстрирует, что чем более равномерно распределены вероятности $p_i$ различных состояний, тем выше неопределенность и, следовательно, энтропия.

Термодинамическая энтропия, традиционно понимаемая как мера беспорядка, приобретает более глубокий смысл, если рассматривать её как отражение недостатка информации о микроскопическом состоянии системы. Вместо того, чтобы фокусироваться на физическом беспорядке, этот подход предполагает, что высокая энтропия указывает на наше незнание точных координат и импульсов каждой частицы в системе. Чем больше возможных микроскопических состояний соответствуют одному макроскопическому состоянию, тем выше энтропия и тем меньше информации у наблюдателя о реальном состоянии системы. Таким образом, энтропия не является свойством самой системы, а скорее отражает степень нашей неопределенности относительно её внутреннего устройства, что делает её фундаментальной величиной в контексте информации и знания.

Исследования демонстрируют, что изменения в объеме информации о системе напрямую связаны с потенциальной возможностью совершения работы над ней или извлечения энергии. Это означает, что получение новых сведений о микроскопическом состоянии системы позволяет теоретически использовать эту информацию для повышения эффективности процессов или получения полезной работы. $W = -k_B T \ln{P}$ — эта связь, где $W$ — работа, $k_B$ — постоянная Больцмана, $T$ — температура, а $P$ — вероятность состояния — подчеркивает, что информация не является абстрактным понятием, а физической величиной, тесно связанной с энергией и термодинамикой. Таким образом, уменьшение неопределенности, то есть получение информации, эквивалентно снижению энтропии и высвобождению энергии, доступной для совершения работы.

Взаимосвязь между информацией, энергией и фундаментальными законами физики представляет собой глубокое и многогранное явление. Исследования показывают, что информация — это не просто абстрактное понятие, а физическая сущность, тесно связанная с энергией и способностью системы совершать работу. Уменьшение неопределенности, то есть получение информации о системе, эквивалентно уменьшению ее энтропии и высвобождению потенциальной энергии, которую можно использовать для выполнения полезной работы. $ΔW = -ΔI$ — эта связь демонстрирует, что изменение информации напрямую связано с изменением доступной энергии. Таким образом, фундаментальные физические законы не просто регулируют движение энергии, но и определяют способы получения, хранения и использования информации, что указывает на ее ключевую роль в функционировании Вселенной.

Данное исследование, разрешая парадокс Гиббса через призму теории информации, демонстрирует, что кажущаяся нестабильность классического статистического подхода — это не недостаток самой теории, а скорее следствие неверной интерпретации энтропии. Подобно тому, как системы неизбежно стареют, классическое ансамблевое описание, представленное в работе, не нуждается в фундаментальном пересмотре. Вместо этого, необходимо признать, что стабильность — это иллюзия, обусловленная временем и кэшированием информации. Как отмечал Фридрих Ницше: «Тот, кто сражается с чудовищами, должен следить, чтобы самому не стать чудовищем». Эта мысль перекликается с необходимостью критически оценивать исходные предположения и избегать упрощенных интерпретаций, даже в рамках устоявшихся научных парадигм.

Что дальше?

Представленная работа, разрешая парадокс Гиббса через призму информационного принципа равной вероятности, скорее не закрывает вопрос, а смещает акцент. Иллюзия противоречия, как демонстрируется, таится не в недостатках классической статистической механики, а в неверной интерпретации энтропии — в попытке рассматривать её как нечто объективное, а не как меру нашего незнания. Системы, подобно речным долинам, неизбежно несут на себе отпечаток времени, и попытки «остановить» этот процесс, зафиксировать состояние «максимальной гармонии», обречены на неудачу.

Однако, предложенный подход лишь частично снимает напряжение. Вопрос о связи информации и физической реальности остается открытым. Необходимо дальнейшее исследование взаимосвязи между энтропией Шеннона и термодинамической энтропией, особенно в контексте систем, далеких от равновесия. Устойчивость классического подхода в условиях экстремальных энергий и квантовых эффектов также требует пристального внимания.

В конечном итоге, парадокс Гиббса — это не ошибка в расчетах, а напоминание о том, что любое описание мира — это всегда упрощение, проекция, отражение нашей ограниченной перспективы. Вместо того, чтобы стремиться к абсолютной точности, следует научиться достойно принимать неизбежное старение любой системы, подобно мудрому садовнику, наблюдающему за сменой времен года.

Оригинал статьи: https://arxiv.org/pdf/2602.06505.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-09 22:03