Размывая границы: Как декогеренция влияет на расчеты возбуждения носителей

от

Автор: Денис Аветисян

Новое исследование показывает, что стандартное правило Ферми оказывается неточным при сильной декогеренции, что необходимо учитывать при моделировании динамики электронов и носителей заряда.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал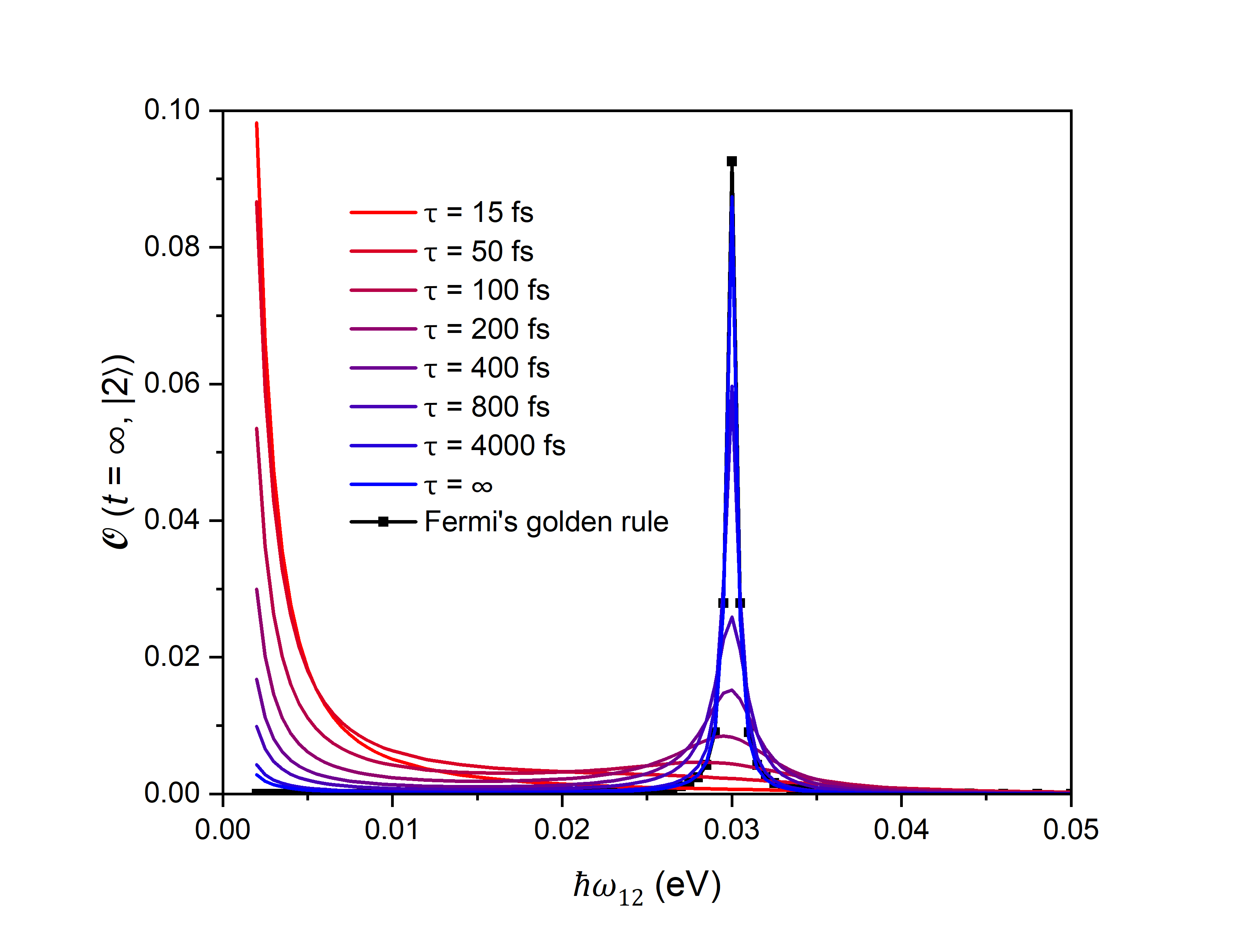
При бесконечном времени, заполненное начальное состояние $ \left|1\right\rangle$ переходит в состояние $ \left|2\right\rangle$, при фиксированной частоте внешнего возмущения $ \hbar\omega = 0.03$ эВ, демонстрируя зависимость этого перехода от величины энергетической щели $ \hbar\omega_{12}$.
При бесконечном времени, заполненное начальное состояние $ \left|1\right\rangle$ переходит в состояние $ \left|2\right\rangle$, при фиксированной частоте внешнего возмущения $ \hbar\omega = 0.03$ эВ, демонстрируя зависимость этого перехода от величины энергетической щели $ \hbar\omega_{12}$.

В статье демонстрируется расхождение между правилом Ферми и расчетами неадиабатической молекулярной динамики при существенных эффектах декогеренции, подчеркивая важность учета этих эффектов для точного моделирования.

В стандартном приближении, правило Ферми описывает скорости переходов между энергетическими уровнями, однако игнорирует влияние декогеренции. В работе, озаглавленной ‘The effects of decoherence on Fermi’s golden rule’, исследуется модификация правила Ферми с учетом эффектов декогеренции, возникающих в результате неадиабатической молекулярной динамики. Показано, что при коротких временах декогеренции наблюдается значительное отклонение от предсказаний стандартного правила Ферми для различных базисов. Может ли учет декогеренции стать ключевым фактором для точного моделирования динамики носителей заряда и электронных переходов в квантовых системах?

Пределы Теории Возмущений: Квантовые Переходы и Их Описание

Описание электронных переходов с помощью правила Ферми основано на приближениях, в частности, на теории слабых возмущений. Данный подход предполагает, что внешнее воздействие на систему незначительно и не вызывает резких изменений в ее состоянии. В рамках этой теории, вероятность перехода между двумя энергетическими уровнями рассчитывается как функция от матричного элемента оператора возмущения и плотности состояний на конечном уровне. Однако, эта модель имеет ограничения: она предполагает линейную зависимость вероятности перехода от интенсивности внешнего воздействия и пренебрегает влиянием окружающей среды на систему. Таким образом, точность расчета, основанного на теории слабых возмущений, существенно снижается при сильных внешних воздействиях или в сложных системах, где взаимодействие с окружающей средой играет значительную роль, что требует применения более сложных методов для адекватного описания динамики возбужденных состояний.

Применение теории возмущений для описания электронных переходов, несмотря на свою эффективность в ряде случаев, сталкивается с ограничениями при сильном внешнем воздействии или существенном влиянии окружающей среды. В этих условиях, когда возмущение перестает быть «малым», стандартные приближения теряют свою точность, приводя к неверным результатам. Окружающая среда, взаимодействуя с системой, вносит дополнительные факторы, которые нельзя игнорировать при расчете вероятности перехода, особенно в случаях, когда энергия взаимодействия с окружением сопоставима с энергией самого перехода. Это особенно критично для систем с узкими энергетическими зазорами, где даже небольшие возмущения могут кардинально изменить динамику возбужденных состояний и, как следствие, оптические и электронные свойства материала.

Традиционные методы моделирования динамики возбужденных состояний сталкиваются с существенными трудностями в непертурбативных режимах, когда внешнее воздействие становится сильным или влияние окружающей среды не может быть пренебрегнуто. Особенно заметны неточности в предсказаниях для систем с энергетическими зазорами в диапазоне от 0.056 до 0.12 эВ, где стандартные приближения теряют свою эффективность. Это приводит к искажению картины перехода между энергетическими уровнями и, как следствие, к неверной интерпретации спектроскопических данных и прогнозированию поведения материала. Развитие более точных методов, учитывающих сильные взаимодействия и влияние окружения, является ключевой задачей современной физики конденсированного состояния и квантовой оптики, позволяющей адекватно описывать поведение сложных квантовых систем.

Результаты моделирования показывают, что при различных частотах внешнего воздействия и фиксированной энергии состояния, метод FGR согласуется с численными расчётами как в фиксированном, так и в адиабатическом базисах, начиная с полностью заполненного состояния.
Результаты моделирования показывают, что при различных частотах внешнего воздействия и фиксированной энергии состояния, метод FGR согласуется с численными расчётами как в фиксированном, так и в адиабатическом базисах, начиная с полностью заполненного состояния.

Декогеренция: Разрушение Квантовой Когерентности

Квантовая декогеренция, представляющая собой потерю квантовой когерентности, принципиально изменяет динамику электронных состояний. В отсутствие декогеренции, электронные состояния могут существовать в суперпозиции, эволюционируя согласно уравнению Шрёдингера. Однако, взаимодействие системы с окружающей средой приводит к потере фазовой информации, разрушая суперпозицию и приводя к переходу к классическому поведению. Это проявляется в угасании интерференционных эффектов и переходе от когерентной эволюции волновой функции к статистическому описанию, управляемому матрицей плотности $ \rho $. Скорость декогеренции зависит от силы взаимодействия системы с окружающей средой и плотности состояний среды, определяя временную шкалу, за которую квантовые эффекты становятся незначительными.

Взаимодействие квантовой системы с окружающей средой, в частности, с фононами в твердых телах, приводит к декогеренции — потере квантовой когерентности. Фононы, являясь квантами колебаний решетки, вызывают рассеяние и фазовую деструкцию квантовых состояний, что проявляется в уменьшении интерференционных эффектов и переходе системы к классическому поведению. Интенсивность взаимодействия с фононами, а следовательно, и скорость декогеренции, зависят от температуры материала и плотности фононов. В результате декогеренции суперпозиции квантовых состояний разрушаются, и система эволюционирует в смешанное состояние, описываемое матрицей плотности $\rho$, что приводит к потере квантовых преимуществ, таких как квантовые вычисления или сверхчувствительные измерения.

Точное моделирование декогеренции требует отказа от теории возмущений в пользу описания полной квантовой эволюции матрицы плотности системы. Это обусловлено тем, что при конечных временах декогеренции отклонения от правила Ферми становятся существенными. Правило Ферми, используемое в теории возмущений для расчета скоростей переходов, предполагает бесконечно малые взаимодействия и не учитывает когерентные эффекты, возникающие при более сильных взаимодействиях с окружающей средой. Для адекватного описания эволюции матрицы плотности, необходимо решать уравнение Линдблада или использовать другие непертурбативные методы, которые позволяют точно учитывать взаимодействие системы с резервуаром и описывать как когерентные, так и некогерентные процессы, влияющие на квантовые состояния.

Неадиабатическая Молекулярная Динамика: Первый Принцип

Неадиабатическая молекулярная динамика (НАМД) представляет собой эффективный метод моделирования квантовой динамики, позволяющий исследовать эволюцию во времени квантовых систем, включая явления декогеренции. В отличие от подходов, основанных на приближениях, НАМД позволяет отслеживать изменения волновой функции системы без ограничений, накладываемых, например, теорией возмущений. Это особенно важно при исследовании процессов, где взаимодействие с окружающей средой играет ключевую роль, приводя к потере квантовой когерентности и переходу к классическому поведению. Метод НАМД позволяет непосредственно рассчитывать эволюцию матрицы плотности $ \rho(t) $, описывающей состояние системы, и, следовательно, моделировать процессы декогеренции и релаксации.

Молекулярная динамика, не являющаяся адиабатической (NAMD), в сочетании с расчетами из первых принципов, позволяет моделировать временную эволюцию волновой функции системы без использования приближений теории возмущений. В отличие от традиционных подходов, требующих упрощения потенциальных поверхностей или использования приближений, NAMD напрямую решает временное уравнение Шредингера для электронных степеней свободы, используя результаты квантово-механических расчетов, таких как теория функционала плотности (DFT) или теория многих тел. Это обеспечивает более точное описание динамики, особенно в областях, где адиабатическое приближение неприменимо, например, при пересечении потенциальных поверхностей или в сильных внешних полях. Такой подход позволяет исследовать процессы, включающие неадиабатические переходы и электронную релаксацию, с высокой степенью реалистичности и точности, без априорных ограничений на форму потенциальной энергии или характер динамики.

Метод P-матрицы обеспечивает эффективное вычисление эволюции матрицы плотности в рамках неадиабатической молекулярной динамики (НАМД), позволяя моделировать эффекты декогеренции. В рамках данного подхода, эволюция матрицы плотности рассчитывается напрямую, избегая приближений, связанных с теорией возмущений. Важно отметить, что результаты, полученные с использованием метода P-матрицы, согласуются с правилом Ферми золотого правила ($2\pi|\langle f | H | i \rangle|^2 \rho(E_f)$) только в предельном случае бесконечного времени декогеренции, что подтверждает корректность реализации данного метода и его способность адекватно описывать квантовую динамику систем.

Численное моделирование двухфононной ТЛС-модели с параметрами ω₁ = 0.047 эВ, ω₂ = 0.020 эВ, V₁ = 0.00001 эВ, V₂ = 0.0001 эВ и Δ = 0.056 эВ подтверждает аналитические результаты, полученные на основе уравнения 28 из приложения, для каждого из фононов (синий и золотой цвета), интерференционных членов (зеленый цвет) и их комбинации (черный цвет).
Численное моделирование двухфононной ТЛС-модели с параметрами ω₁ = 0.047 эВ, ω₂ = 0.020 эВ, V₁ = 0.00001 эВ, V₂ = 0.0001 эВ и Δ = 0.056 эВ подтверждает аналитические результаты, полученные на основе уравнения 28 из приложения, для каждого из фононов (синий и золотой цвета), интерференционных членов (зеленый цвет) и их комбинации (черный цвет).

Моделирование Динамики в Монослое WS2

Монослой дисульфида вольфрама ($WS_2$) представляет собой исключительную платформу для проверки достоверности подхода NAMD. Этот материал демонстрирует выраженное взаимодействие со светом, что делает его чувствительным к воздействию электромагнитного излучения. Наряду с этим, в $WS_2$ наблюдаются значительные эффекты декогеренции — потеря квантовой информации из-за взаимодействия с окружающей средой. Именно сочетание сильного свето-материального взаимодействия и выраженной декогеренции позволяет эффективно тестировать и валидировать методы моделирования динамики возбужденных состояний, такие как NAMD, обеспечивая уверенность в точности предсказаний относительно оптико-электронных свойств этого перспективного материала.

В рамках исследования динамики в монослое $WS_2$ была продемонстрирована высокая точность предсказания поведения возбужденных состояний с использованием подхода NAMD. Применяя как фиксированный, так и адиабатический базис в рамках двухуровневой системы, удалось достоверно смоделировать влияние энергии фононов (0.047 эВ, 0.020 эВ) и силы электрон-фононного взаимодействия (0.00001 эВ, 0.0001 эВ) на эволюцию возбужденных состояний. Полученные результаты указывают на возможность детального изучения механизмов релаксации и декогеренции в этом материале, что критически важно для понимания и оптимизации его оптоэлектронных свойств.

Моделирование показывает, что декогеренция существенно изменяет процесс возбуждения носителей заряда в монослое $WS_2$, оказывая значительное влияние на его оптоэлектронные свойства. В частности, установлено, что степень влияния декогеренции зависит от величины запрещенной зоны материала, которая варьируется от 0.056 эВ при растяжении до 0.12 эВ при сжатии. Изменение запрещенной зоны, вызванное механическим напряжением, влияет на скорость и эффективность возбуждения носителей, что, в свою очередь, определяет оптические и электрические характеристики материала. Таким образом, учет декогеренции является критически важным для точного предсказания поведения и оптимизации свойств монослоя $WS_2$ в различных оптоэлектронных приложениях.

Моделирование NAMD показало, что изменение энергии запрещенной зоны (0.056 эВ при растяжении, 0.067 эВ в нейтральном состоянии и 0.12 эВ при сжатии) связано с возбуждением переносчика заряда и взаимодействием с двумя фононами с энергиями 0.046 и 0.020 эВ, исходя из начального состояния на VBM-2.
Моделирование NAMD показало, что изменение энергии запрещенной зоны (0.056 эВ при растяжении, 0.067 эВ в нейтральном состоянии и 0.12 эВ при сжатии) связано с возбуждением переносчика заряда и взаимодействием с двумя фононами с энергиями 0.046 и 0.020 эВ, исходя из начального состояния на VBM-2.

Исследование влияния декогеренции на правило Ферми демонстрирует, как стандартные упрощения могут искажать картину квантовых процессов. Подобно тому, как сложность рассеивает внимание, а ясность открывает истину, так и учет декогеренции в неадиабатической молекулярной динамике позволяет достичь более точного моделирования возбуждения носителей и динамики электронов. Как заметил Эрвин Шрёдингер: «Нельзя сказать, что реальность существует независимо от наблюдателя». Это высказывание находит отражение в данной работе, где взаимодействие системы с окружающей средой, приводящее к декогеренции, оказывает существенное влияние на наблюдаемые результаты и требует пересмотра устоявшихся подходов к моделированию.

Что дальше?

Попытки упростить реальность посредством золотого правила Ферми, не учитывая декогеренцию, оказались не столь безупречными, как представлялось. Расхождение с расчетами неадиабатической молекулярной динамики — не ошибка метода, а указание на необходимость более честного подхода к описанию динамики носителей. Иллюзия когерентности, столь удобная для теоретических построений, тает при столкновении с расчетами из первых принципов.

Предстоящая работа требует переосмысления самой концепции скорости перехода. Достаточно ли формальных поправок к золотому правилу, или необходим принципиально иной подход, учитывающий не только взаимодействие с окружением, но и структуру самой декогеренции? Вопрос не в увеличении точности, а в адекватности модели. В конечном итоге, красота формулы — лишь побочный эффект структурной честности.

Перспективы применения в квантовых вычислениях и моделировании электронных процессов очевидны. Однако, истинная ценность этого направления заключается не в предсказании конкретных результатов, а в признании границ применимости существующих моделей. Умение признать незнание — начало мудрости, и, возможно, ключ к пониманию более глубоких процессов.

Оригинал статьи: https://arxiv.org/pdf/2511.21238.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2025-11-28 19:57