Рождение частиц из вакуума в искривленном пространстве: новый подход

Автор: Денис Аветисян

Исследование предлагает вычислительный метод для изучения процесса рождения пар фермионов в нетривиальных гравитационных полях.

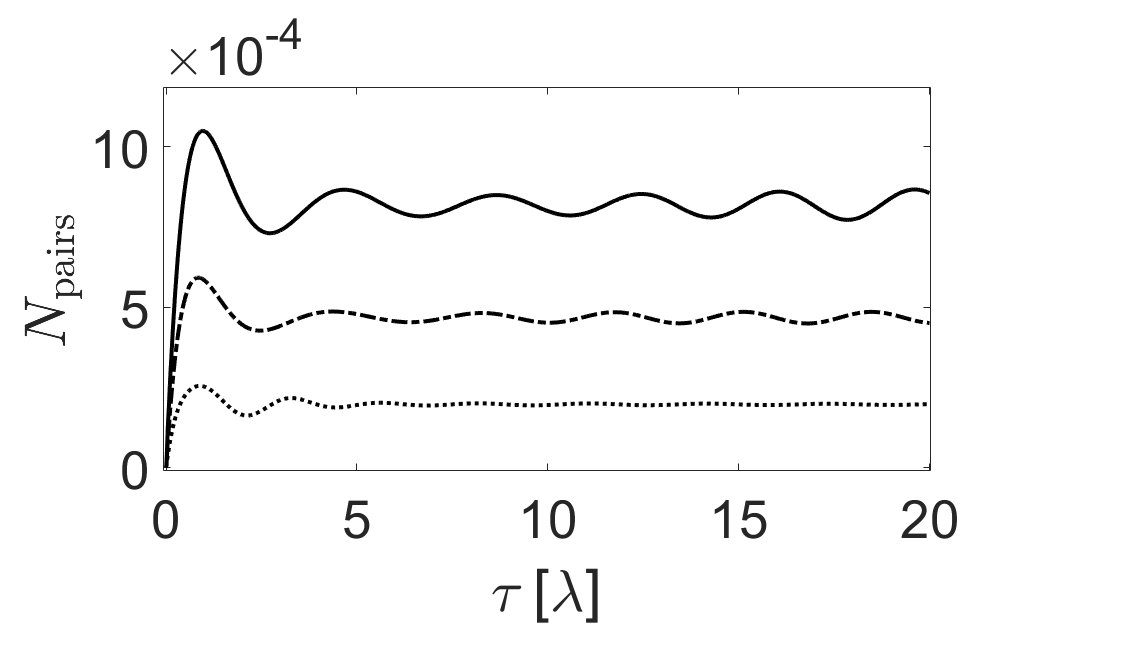
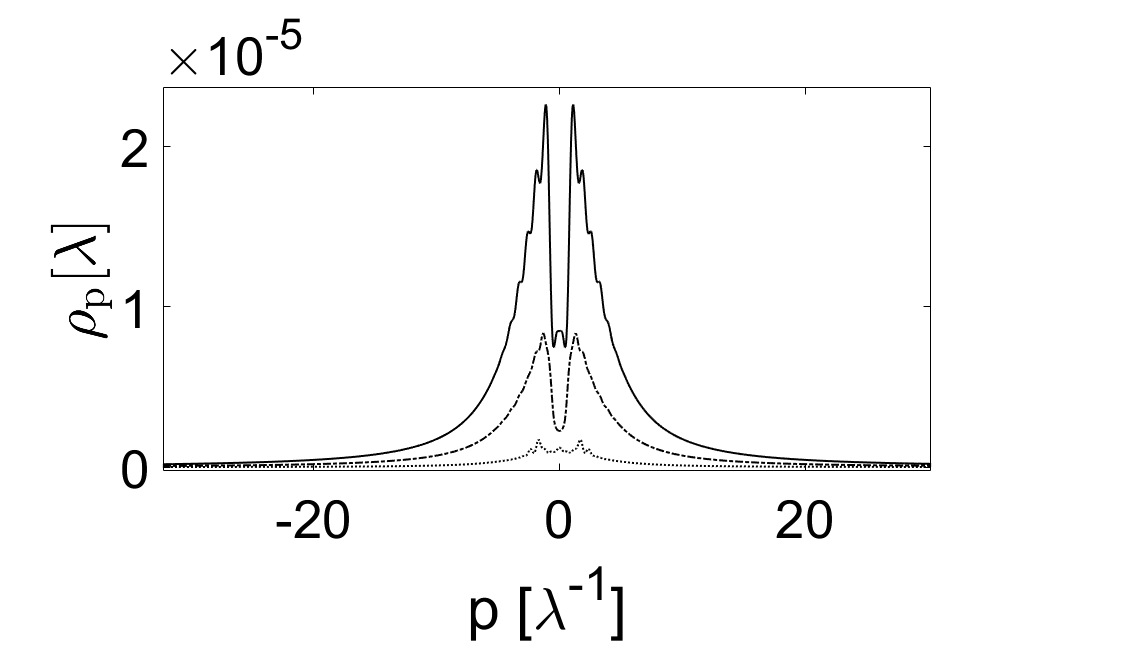
Наблюдения показывают, как плотность создаваемых пар фермион-антифермион и их импульсной спектр изменяются во времени τ при значениях <span class="katex-eq" data-katex-display="false">0.1\,\lambda</span>, <span class="katex-eq" data-katex-display="false">1.3\,\lambda</span> и <span class="katex-eq" data-katex-display="false">10\,\lambda</span>, где λ - комптоновская длина волны электрона, при этом кривая Риччи скаляра <span class="katex-eq" data-katex-display="false">R(\xi)[latex], вычисленная из уравнений (24) и (25) при [latex]\beta = \tfrac{1}{2}</span>, отражает искривление пространства-времени, полученное на сетке из <span class="katex-eq" data-katex-display="false">N = 2^{11}</span> точек с временным шагом <span class="katex-eq" data-katex-display="false">\delta\tau = 0.01\,\lambda</span>. — Наблюдения показывают, как плотность создаваемых пар фермион-антифермион и их импульсной спектр изменяются во времени τ при значениях $0.1\,\lambda$ , $1.3\,\lambda$ и $10\,\lambda$ , где λ — комптоновская длина волны электрона, при этом кривая Риччи скаляра $R(\xi)[latex], вычисленная из уравнений (24) и (25) при [latex]\beta = \tfrac{1}{2}$ , отражает искривление пространства-времени, полученное на сетке из $N = 2^{11}$ точек с временным шагом $\delta\tau = 0.01\,\lambda$ .

В работе представлен численный фреймворк, основанный на методе расщепленного оператора, для изучения квантовой теории поля в искривленных двумерных пространствах.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал

Несмотря на известное предсказание о создании частиц в сильных электромагнитных полях, аналогичный эффект в искривленных пространствах-временах остается малоизученным. В работе «Computational quantum field theory for fermion pair creation in 2-dimensional curved spacetimes» представлен численный подход, основанный на расширении метода вычислительной квантовой теории поля (CQFT), для исследования рождения пар фермионов в искривленных двухмерных пространствах. Разработанная методика позволяет моделировать возбуждение вакуума поля Дирака под воздействием локализованного искажения кривизны пространства-времени. Каковы перспективы применения этого подхода для изучения динамических процессов рождения частиц в более сложных, эволюционирующих гравитационных полях и в присутствии электромагнитного излучения?

Рождение частиц из вакуума: от теории к реальности

Описание рождения частиц требует перехода от упрощенных моделей плоского пространства-времени к более реалистичному представлению искривленного пространства-времени. В контексте квантовой теории поля, вакуум не является абсолютно пустым, а представляет собой состояние с постоянным возникновением и аннигиляцией виртуальных частиц. Однако, в искривленном пространстве-времени, например, вблизи черной дыры или во время космологической инфляции, эти виртуальные частицы могут приобретать реальную энергию и становиться наблюдаемыми. Это связано с тем, что гравитация, как проявление искривления пространства-времени, может служить источником энергии для этих частиц, нарушая обычные условия сохранения энергии в плоском пространстве. Изучение этого процесса требует использования математических инструментов, способных адекватно описывать геометрию искривленного пространства-времени и ее влияние на квантовые поля, что позволяет исследовать фундаментальные вопросы о природе вакуума и происхождении частиц во Вселенной.

Тетрадный формализм играет ключевую роль в описании искривленного пространства-времени, обеспечивая мост между локальными системами отсчета, в которых действуют законы специальной теории относительности, и глобальными координатами искривленного пространства. Этот подход позволяет рассматривать искривленное пространство-время как совокупность локальных, плоских пространств Минковского, связанных преобразованиями тетрад. По сути, тетрады - это наборы из четырех векторных полей, которые определяют базис в каждой точке пространства-времени и устанавливают соответствие между координатами в локальной и глобальной системах. Благодаря этому, сложные вычисления в искривленном пространстве-времени сводятся к более простым операциям в локальных, плоских системах отсчета, что значительно упрощает анализ физических процессов, происходящих в сильных гравитационных полях. Такой подход особенно важен при изучении астрофизических объектов, таких как черные дыры и нейтронные звезды, где искривление пространства-времени становится крайне значительным и требует точного математического описания.

Для корректного описания поведения спинорных полей в искривленном пространстве-времени необходимо тщательно учитывать влияние спинорного соединения и ковариантной производной. В отличие от плоского пространства, где спиноры преобразуются простым образом, в искривленном пространстве-времени требуется введение спинорного соединения, которое описывает изменение спиноров при параллельном переносе. Ковариантная производная, включающая как обычную производную, так и спинорное соединение, обеспечивает правильное преобразование спинорных полей при изменении координат. Игнорирование этих факторов приводит к некорректным результатам и нарушению ковариантности, что особенно критично при изучении физических процессов в сильных гравитационных полях, например, вблизи черных дыр или в ранней Вселенной. Формулировка уравнения Дирака с учетом этих особенностей позволяет адекватно описывать поведение фермионов в искривленном пространстве-времени и предсказывать различные эффекты, такие как излучение Хокинга или генерация пар частиц.

Количество созданных пар фермион-антифермион увеличивается с увеличением ширины гауссовой кривизны <span class="katex-eq" data-katex-display="false">r_0</span>, при этом насыщение достигается позднее и для большего числа пар. — Количество созданных пар фермион-антифермион увеличивается с увеличением ширины гауссовой кривизны $r_0$ , при этом насыщение достигается позднее и для большего числа пар.

Упрощение сложности: конформная плоскостность и вычислительные методы

Использование гауссова искажения плоского пространства-времени представляет собой упрощенную, но эффективную модель для исследования искривленного пространства-времени. Вместо решения сложных уравнений общей теории относительности для произвольных метрик, гауссово искажение позволяет ввести контролируемую кривизну, описываемую параметром, связанным со стандартным отклонением гауссовой функции. Это позволяет проводить систематические исследования влияния кривизны на различные физические процессы, такие как распространение частиц и квантовые флуктуации, при сохранении аналитической и вычислительной трактабельности. В частности, этот подход позволяет изучать эффекты, возникающие при малых отклонениях от плоского пространства-времени, что особенно важно для анализа космологических возмущений и излучения Хокинга.

Использование конформной плостности, достигаемой посредством использования нуль-координат, значительно упрощает как аналитические вычисления, так и вычислительную сложность при решении задач в искривлённом пространстве-времени. Преобразование к конформной системе координат позволяет свести метрику пространства-времени к виду, эквивалентному плоскому пространству, что упрощает дифференциальные уравнения и алгоритмы численного моделирования. Это позволяет существенно снизить требования к вычислительным ресурсам и времени, необходимым для получения результатов, по сравнению с прямым решением уравнений в искривлённом пространстве-времени. При этом сохраняется физическая корректность модели, поскольку конформные преобразования не меняют причинных связей и физических наблюдаемых.

Вычислительная квантовая теория поля (ВККТП) расширяет инструментарий квантовой теории поля для применения к искривленным пространствам-временам, позволяя проводить симуляции в реальном времени. В рамках проведенных исследований была достигнута сходимость при пространственном разрешении сетки $\Delta\xi = 0.0488\lambda$ и временном шаге $\Delta\tau = 0.01\lambda$ . Данные параметры указывают на возможность проведения численных расчетов с заданной точностью в условиях искривленного пространства-времени, что открывает перспективы для изучения динамических процессов в гравитационных полях.

Спектр создаваемых пар фермион-антифермион демонстрирует увеличение количества создаваемых мод при увеличении силы гауссовой кривизны, причём насыщение достигается при больших значениях, как видно на графиках для <span class="katex-eq" data-katex-display="false">eta = 0.8</span> (сплошная линия) и <span class="katex-eq" data-katex-display="false">eta = 0.5</span> (пунктирная линия). — Спектр создаваемых пар фермион-антифермион демонстрирует увеличение количества создаваемых мод при увеличении силы гауссовой кривизны, причём насыщение достигается при больших значениях, как видно на графиках для $eta = 0.8$ (сплошная линия) и $eta = 0.5$ (пунктирная линия).

Динамика вакуума и создание пар: свидетельство рождения частиц

Исследование показало, что эффекты кривизны пространства-времени являются движущей силой для возбуждения квантового вакуума, приводя к спонтанному образованию пар частица-античастица. В состоянии с нулевой энергией, вакуум не является абсолютно пустым, а характеризуется постоянными квантовыми флуктуациями. При наличии сильного гравитационного поля, обусловленного кривизной, эти флуктуации усиливаются, приводя к возникновению виртуальных частиц. При достаточно высокой энергии, эти виртуальные частицы могут стать реальными, формируя пары частица-античастица, что представляет собой наблюдаемый эффект генерации частиц из вакуума. Данный процесс демонстрирует прямую связь между геометрией пространства-времени и динамикой квантовых полей.

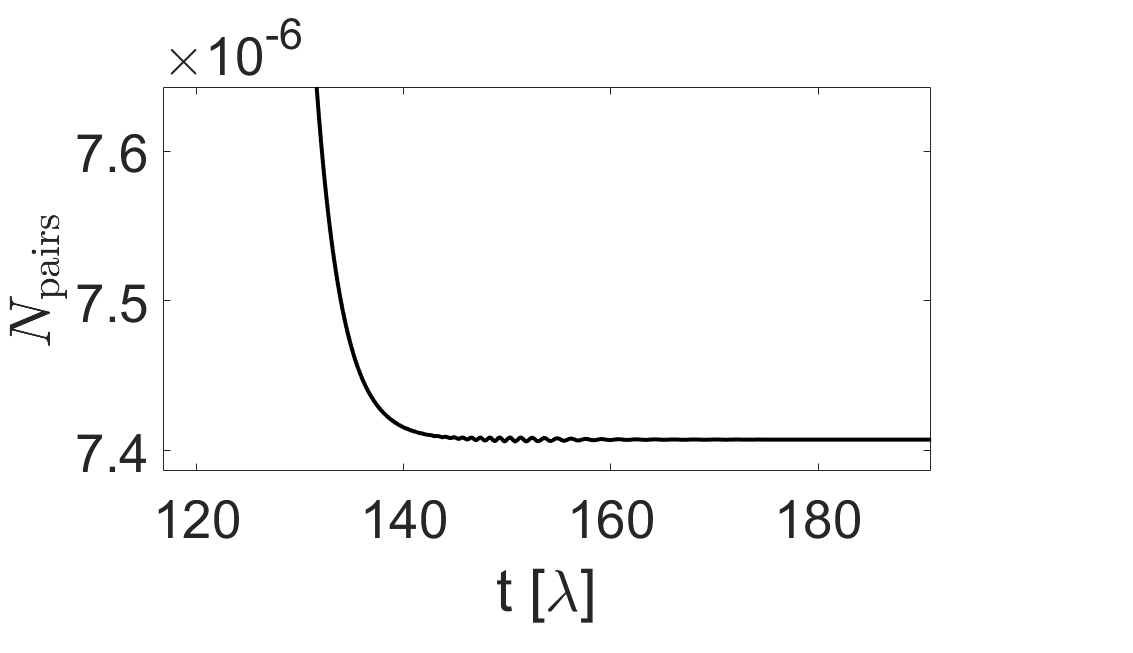
Для эффективного приближения оператора временной эволюции в симуляциях динамики вакуума использован метод разделения операторов (split-operator method). Этот метод позволяет разложить сложный оператор временной эволюции на последовательность более простых операторов, каждый из которых описывает отдельную физическую составляющую системы. Применение метода разделения операторов значительно снижает вычислительные затраты и обеспечивает возможность моделирования динамики вакуума в реальном времени, сохраняя при этом высокую точность приближения. В данной работе точность реализованной схемы подтверждена сохранением нормы на уровне 3.4 x 10^-13 в течение времени симуляции, равного 20λ.

В ходе моделирования продемонстрировано, что оператор временной эволюции точно воспроизводит процесс рождения пар частиц. Достигнутая высокая точность, подтвержденная сохранением нормы $3.4 \times 10^{-{13}}$ на протяжении времени моделирования $20\lambda$ , позволяет достоверно исследовать влияние искривления пространства-времени на наблюдаемое производство частиц. Полученные результаты подтверждают, что искривление пространства-времени действительно может служить причиной возникновения пар частиц из вакуума, что имеет важное значение для понимания физики высоких энергий и космологии.

Численное моделирование процесса образования пар фермион-антифермион в шаге Сотера при <span class="katex-eq" data-katex-display="false">E_0 = 1/4</span> и <span class="katex-eq" data-katex-display="false">\omega = 0.1</span> показывает, что асимптотическое число образованных пар составляет приблизительно <span class="katex-eq" data-katex-display="false">7.4 \times 10^{-6}</span>, что согласуется с теоретическими предсказаниями для адиабатического режима, и не зависит от разрешения сетки. — Численное моделирование процесса образования пар фермион-антифермион в шаге Сотера при $E_0 = 1/4$ и $\omega = 0.1$ показывает, что асимптотическое число образованных пар составляет приблизительно $7.4 \times 10^{-6}$ , что согласуется с теоретическими предсказаниями для адиабатического режима, и не зависит от разрешения сетки.

Значение результатов и перспективы исследований: за пределами модели

Представленная работа закладывает важнейший фундамент для понимания процессов рождения частиц в астрофизических средах, характеризующихся сильными гравитационными полями. Исследование демонстрирует, что вблизи компактных объектов, таких как черные дыры или нейтронные звезды, квантовые флуктуации вакуума могут приводить к наблюдаемому появлению частиц, что существенно влияет на энергетический баланс этих объектов и их окружения. Полученные результаты позволяют более точно моделировать физические процессы, происходящие в экстремальных условиях, и открывают перспективы для изучения взаимодействия гравитации и квантовой механики в реальных астрофизических сценариях. Особое значение имеет возможность применения этих знаний для анализа таких явлений, как аккреционные диски вокруг черных дыр и процессы, происходившие в ранней Вселенной, где гравитационные эффекты играли доминирующую роль.

Разработанные методы открывают возможности для исследования более реалистичных искривленных пространств-времен, выходящих за рамки упрощенных моделей. Это позволяет перейти к изучению сложного взаимодействия между гравитацией и квантовыми полями в экстремальных условиях. Использование этих подходов потенциально способно раскрыть новые аспекты физики черных дыр и других астрофизических объектов, где гравитационные эффекты проявляются наиболее сильно. Дальнейшие исследования в этом направлении могут привести к более глубокому пониманию фундаментальных законов природы, объединяющих гравитацию и квантовую механику, и предоставить инструменты для анализа сложных физических процессов, происходящих во Вселенной. Особенно перспективным представляется применение этих методов для моделирования динамики частиц вблизи сингулярностей и для изучения влияния квантовых флуктуаций на геометрию пространства-времени.

Дальнейшие исследования, использующие разработанные методы, могут быть направлены на анализ таких фундаментальных явлений, как излучение Хокинга и процессы, происходившие в ранней Вселенной. Изучение излучения Хокинга позволит проверить предсказания квантовой теории гравитации в экстремальных условиях, а моделирование условий ранней Вселенной, в частности, эпохи инфляции, может пролить свет на происхождение крупномасштабной структуры космоса и природу тёмной материи. Применение этих техник к изучению космологических моделей, учитывающих кривизну пространства-времени, позволит более точно определить параметры Вселенной и расширить наше понимание её эволюции. Такой подход открывает перспективы для углубленного анализа взаимосвязи между гравитацией и квантовыми полями, приближая нас к созданию единой теории, описывающей все фундаментальные взаимодействия во Вселенной.

Представленное исследование, расширяющее возможности вычислительной квантовой теории поля для искривленных пространств-времен, демонстрирует границы применимости даже самых изящных математических моделей. Подобно тому, как горизонт событий черной дыры скрывает сингулярность, так и вычислительные методы сталкиваются с ограничениями при моделировании экстремальных физических условий. Юрген Хабермас однажды заметил: «Коммуникативное действие направлено на достижение взаимопонимания». В контексте данной работы, это можно интерпретировать как стремление к более глубокому пониманию квантового вакуума и процессов рождения пар фермионов, несмотря на вычислительные сложности и теоретические неопределенности, возникающие в искривленных пространствах. Чёрные дыры, как и сложные математические модели, требуют постоянной проверки и переосмысления.

Что дальше?

Представленная работа, расширяющая возможности вычислительной квантовой теории поля для искривлённых пространств-времён, лишь приоткрывает завесу над бездной. Возможность численно исследовать создание пар фермионов в нетривиальных геометриях - это, безусловно, шаг вперёд, но иллюзия полного понимания столь же опасна, как приближение к горизонту событий. Любая модель, даже самая изящная, остаётся лишь эхом наблюдаемого, а за горизонтом - темнота, где привычные понятия теряют смысл.

Очевидно, что дальнейшее развитие требует преодоления ограничений численных методов. Увеличение точности и масштабируемости расчётов, а также учёт более сложных геометрий и взаимодействий - задачи, которые кажутся тривиальными, пока не столкнёшься с ними напрямую. Если же кто-то полагает, что постиг сингулярность, следует помнить: гордыня - предшественник заблуждений.

Более глубокое осмысление полученных результатов потребует не только математической строгости, но и философской рефлексии. Изучение квантового вакуума в искривлённом пространстве - это не просто физическая проблема, это попытка заглянуть в первозданную тьму, где рождаются и исчезают вселенные. И, возможно, осознание собственной незначительности перед лицом этой бездны - самое важное открытие, которое можно сделать.

Оригинал статьи: https://arxiv.org/pdf/2602.07330.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-10 11:36