Сквозь хаос: Моделирование распространения света в турбулентной среде

Автор: Денис Аветисян

Новая математическая модель описывает, как свет ведет себя в сложных, меняющихся во времени средах, таких как атмосферная турбулентность и случайные оптические среды.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал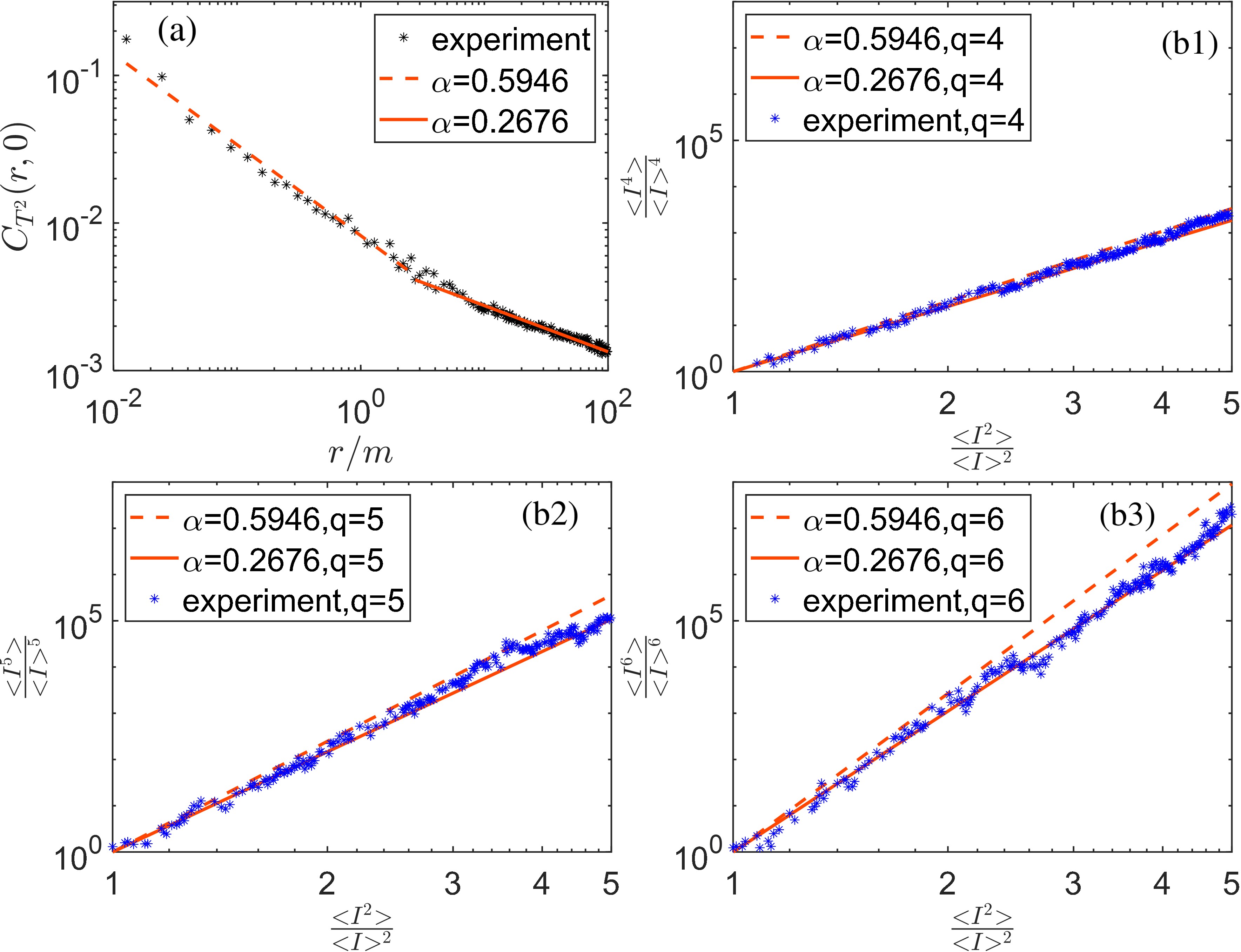

На основе анализа данных, полученных с помощью датчиков TempVue 20 Pt100, установлено, что зависимость квадрата показателя преломления от расстояния между точками измерений описывается кусочно-линейной аппроксимацией, а отношение <span class="katex-eq" data-katex-display="false">\frac{\langle I^{q}\rangle}{\langle I\rangle^{q}}\big|\_{\boldsymbol{x}\_{0}}</span> к <span class="katex-eq" data-katex-display="false">\frac{\langle I^{2}\rangle}{\langle I\rangle^{2}}\big|\_{\boldsymbol{x}\_{0}}</span> при <span class="katex-eq" data-katex-display="false">q=4,5,6</span> и апертуре приемника 2 мм демонстрирует логарифмическую зависимость, подтверждающую корректность уравнения (13). — На основе анализа данных, полученных с помощью датчиков TempVue 20 Pt100, установлено, что зависимость квадрата показателя преломления от расстояния между точками измерений описывается кусочно-линейной аппроксимацией, а отношение $\frac{\langle I^{q}\rangle}{\langle I\rangle^{q}}\big|\_{\boldsymbol{x}\_{0}}$ к $\frac{\langle I^{2}\rangle}{\langle I\rangle^{2}}\big|\_{\boldsymbol{x}\_{0}}$ при $q=4,5,6$ и апертуре приемника 2 мм демонстрирует логарифмическую зависимость, подтверждающую корректность уравнения (13).

Исследование основано на стохастических частных дифференциальных уравнениях и учитывает немарковские характеристики и пространственные корреляции для точного моделирования распространения света.

Несмотря на значительные успехи в оптической связи и визуализации, описание распространения света в быстро меняющихся, неоднородных средах остается сложной задачей. В работе, посвященной ‘Study on Light Propagation through Space-Time Random Media via Stochastic Partial Differential Equations’, предложена новая стохастическая модель, использующая уравнения в частных производных для описания влияния временных и пространственных корреляций на характеристики светового поля. Показано, что гиперболический вариант модели Андерсона адекватно описывает распространение света в таких средах, а полученные количественные характеристики стохастических свойств позволяют более точно прогнозировать поведение световых полей. Какие перспективы открывает разработанный подход для повышения эффективности систем оптической связи и изображений в условиях турбулентной атмосферы и других случайных средах?

Понимание Случайных Средах: Необходимость Новых Инструментов

Многие природные и искусственные системы, от распределения света в биологических тканях до распространения сейсмических волн в земной коре и работы современных материалов, демонстрируют характеристики случайных сред. Это создает значительные трудности для традиционных методов моделирования, которые часто опираются на упрощающие предположения о регулярности и однородности среды. В таких системах свойства среды варьируются непредсказуемо в пространстве, что приводит к сложным процессам рассеяния, поглощения и отражения, которые не могут быть адекватно описаны стандартными подходами. Поэтому, для эффективного анализа и прогнозирования поведения этих систем требуется разработка новых, более совершенных инструментов и моделей, способных учитывать стохастическую природу случайных сред и сложные корреляции между их компонентами.

Для адекватного описания случайных сред необходимо отказаться от упрощающих предположений об их однородности и изотропности. Традиционные модели часто исходят из того, что свойства среды одинаковы во всех точках и направлениях, что в реальности встречается редко. Однако, в большинстве природных и искусственных систем, характеристики среды флуктуируют, демонстрируя сложные корреляции между различными точками пространства. Это означает, что значение свойства в одной точке тесно связано со значениями в соседних точках, причем эта связь может зависеть от направления и расстояния. Игнорирование этих корреляций приводит к неточным прогнозам и неадекватным моделям, поэтому для точного описания случайных сред требуется разработка новых методов и инструментов, способных учитывать их сложную и анизотропную структуру. Исследование этих корреляций позволяет лучше понимать распространение волн, перенос энергии и вещества в таких средах, открывая возможности для создания новых материалов и технологий.

Дробное Броуновское Движение: Улавливая Долгосрочные Зависимости

Дробное броуновское движение (fBm) представляет собой математический аппарат, позволяющий моделировать временные корреляции в случайных средах. В отличие от традиционного броуновского движения, fBm характеризуется параметром Херста $H$ , определяющим степень самоподобия и, следовательно, долгосрочных зависимостей в процессе. Это позволяет описывать системы, где текущее значение зависит не только от непосредственного прошлого, но и от более удаленных событий во времени. Математически, fBm определяется как гауссовский процесс с нулевым средним и функцией автокорреляции, пропорциональной $|t-s|^{2H-1}$ , где $t$ и $s$ — моменты времени. При $0 < H < 0.5$ процесс демонстрирует антиперсистентность (тенденцию к развороту тренда), при $H > 0.5$ — персистентность (продолжение тренда), а при $H = 0.5$ соответствует стандартному броуновскому движению.

Индекс Херста является ключевым параметром для количественной оценки долгосрочных зависимостей во фрактальном броуновском движении. Его значение, находящееся в диапазоне от 0 до 1, определяет характер корреляций во временном ряду: значения больше 0.5 указывают на устойчивое (persistent) поведение, когда положительные и отрицательные отклонения имеют тенденцию к продолжению в том же направлении; значения меньше 0.5 свидетельствуют о антиустойчивом (anti-persistent) поведении, характеризующемся чередованием отклонений; значение равное 0.5 соответствует случайному броуновскому движению без долгосрочных зависимостей. $H$ напрямую влияет на функцию автокорреляции процесса, определяя скорость её затухания и, следовательно, степень влияния прошлых значений на текущее.

В отличие от более простых моделей, фрактальное броуновское движение (fBm) способно моделировать как устойчивое (persistent), так и антиустойчивое (anti-persistent) поведение временных рядов, что обеспечивает более реалистичное описание сложных систем. Экспериментальные данные демонстрируют снижение корреляции с увеличением апертуры: коэффициент корреляции Пирсона составил 0.905 при апертуре 2 мм, в то время как при апертуре 300 мм этот показатель снизился до 0.341. Данный результат указывает на зависимость корреляционных свойств от масштаба наблюдения и подтверждает применимость fBm для анализа систем с долгосрочными зависимостями.

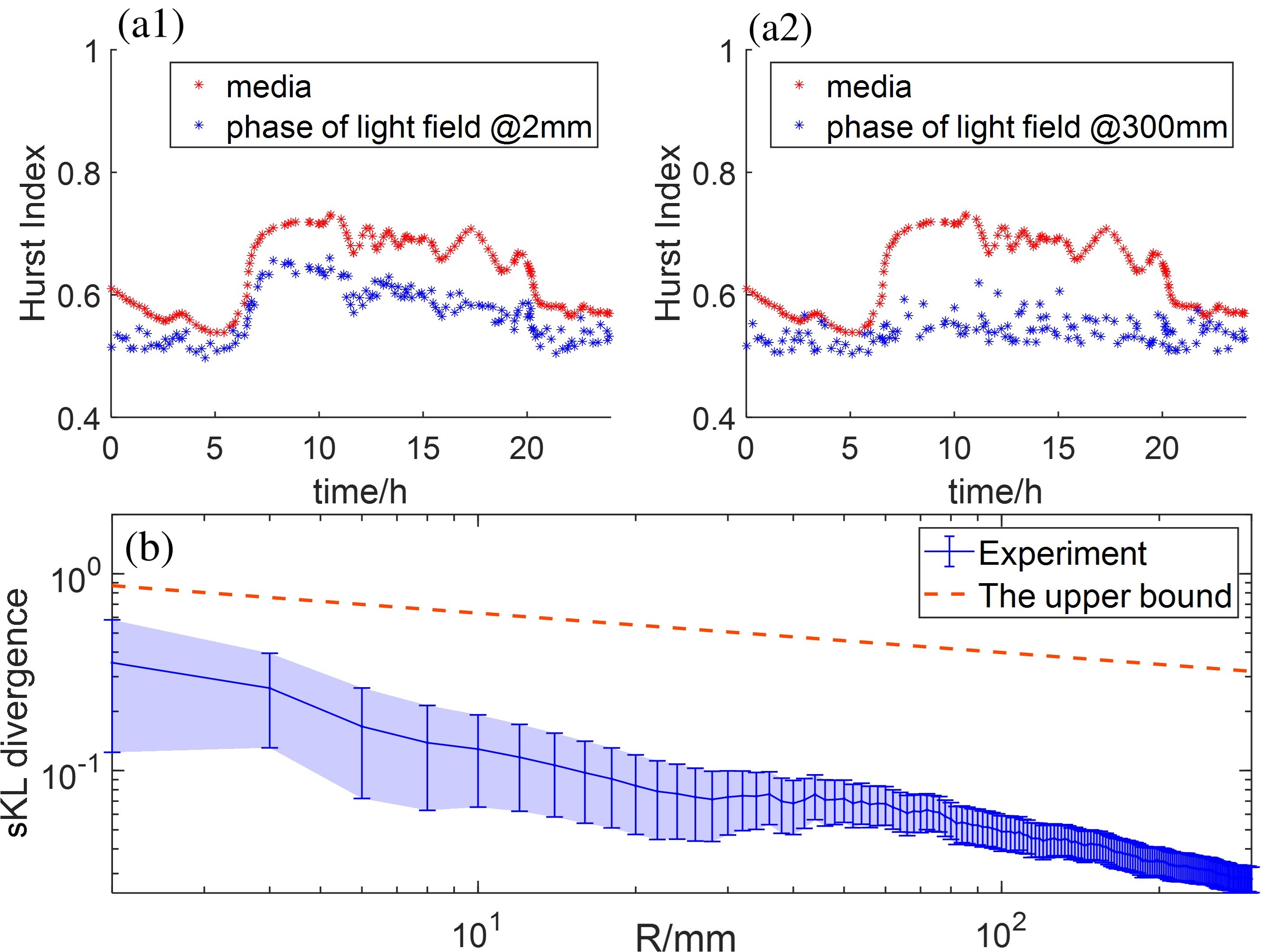
Изменение корреляции между <span class="katex-eq" data-katex-display="false">\mu(t_{i}, \boldsymbol{x}_{0})</span> и <span class="katex-eq" data-katex-display="false">\varphi(t_{i})</span> указывает на зависимость от апертуры: при 2 мм наблюдается высокая корреляция (коэффициент Пирсона 0.905), которая снижается до незначительной при 300 мм, что подтверждается анализом расхождения Кульбака-Лейблера <span class="katex-eq" data-katex-display="false">Z_{R}(t)</span> и <span class="katex-eq" data-katex-display="false">\mathcal{N}_{t}(0,1)</span> и соответствует уравнениям (14) и (16). — Изменение корреляции между $\mu(t_{i}, \boldsymbol{x}_{0})$ и $\varphi(t_{i})$ указывает на зависимость от апертуры: при 2 мм наблюдается высокая корреляция (коэффициент Пирсона 0.905), которая снижается до незначительной при 300 мм, что подтверждается анализом расхождения Кульбака-Лейблера $Z_{R}(t)$ и $\mathcal{N}_{t}(0,1)$ и соответствует уравнениям (14) и (16).

Оценка Херста: Анализ Рескалированного Диапазона на Практике

Метод рескалированного диапазона (RRA) является широко используемым подходом к оценке индекса Херста по данным временных рядов. В основе метода лежит анализ диапазона кумулятивных отклонений от среднего значения, который нормализуется относительно стандартного отклонения и интервала времени. Индекс Херста, полученный с помощью RRA, характеризует долгосрочную память временного ряда и позволяет оценить его стационарность и фрактальную размерность. Метод применяется в различных областях, включая гидрологию, финансы и анализ климатических данных, для оценки устойчивости и предсказуемости временных процессов.

Метод рескалированного диапазона (RRA) предполагает анализ диапазона кумулятивных отклонений временного ряда от среднего значения. Этот диапазон нормируется путем деления на стандартное отклонение ряда и длину временного интервала. $R/S$ — это отношение рескалированного диапазона $R$ к стандартному отклонению $S$ . Вычисление $R/S$ производится для различных длин временных интервалов $n$ . Затем, оценивается зависимость $R/S$ от $n$ . По наклону этой зависимости в логарифмическом масштабе определяется показатель Херста $H$ , который характеризует долговременную память временного ряда.

Анализ изменённого диапазона (RRA) предполагает, что временной ряд обладает свойствами самоподобия и долгой памяти, что необходимо для корректной оценки индекса Херста. Однако, RRA чувствителен к нарушениям этих предположений. В частности, наличие в данных трендов, автокорреляции, или нестационарности может приводить к систематическим ошибкам в оценке. Кроме того, RRA восприимчив к шуму, поскольку шум увеличивает диапазон колебаний, что может привести к завышенной оценке индекса Херста, особенно при анализе коротких временных рядов. Для повышения надежности оценки рекомендуется предварительная обработка данных, включающая удаление тренда и фильтрацию шума, а также использование альтернативных методов оценки индекса Херста.

Пространственные Корреляции и Спектры Степенных Законов

Пространственная корреляция скалярных полей в случайных средах зачастую описывается спектром степенных законов. Данный спектр представляет собой математическое выражение, демонстрирующее, как сила корреляции между точками в среде уменьшается с увеличением расстояния между ними. По сути, он раскрывает скрытую структуру среды, указывая на преобладающие масштабы неоднородностей и характер турбулентности. Спектр степенных законов позволяет исследователям понять, насколько сильно связаны различные части среды, и как эти связи влияют на распространение волн или других физических явлений внутри нее. Например, анализ этого спектра может выявить наличие фрактальных структур или степенных зависимостей, что является ключевым для понимания поведения света в тумане, звука в океане или тепла в турбулентном потоке.

Спектр степенных законов, описывающий корреляцию скалярных полей в случайных средах, предоставляет ценную информацию о структуре этой среды на различных масштабах. Уменьшение силы корреляции с увеличением расстояния не является случайным процессом, а отражает определенные закономерности, присущие внутренней организации среды. Изучение скорости этого затухания позволяет выявить преобладающие масштабы неоднородностей, а также характер турбулентности или других процессов, формирующих структуру среды. Таким образом, анализ степенного спектра выступает мощным инструментом для неразрушающего исследования внутренней организации материалов и сред, позволяя делать выводы об их физических свойствах и процессах, происходящих внутри.

Расширенная самоподобие (ESS) предоставляет количественную характеристику различных турбулентных паттернов посредством индикатора степенного закона. Экспериментальная установка, включающая лазер с шириной линии 0.85 кГц и промежуточную частоту (IF) 80 МГц, обеспечила точные измерения амплитуды и фазы. Ширина бина STFT, равная 10 кГц, превышает частоту Найквиста для масштаба флуктуаций среды (примерно 1 кГц), что гарантирует корректную обработку данных. Полученные экспериментальные результаты подтверждают теоретическую верхнюю границу для дивергенции sKL, которая масштабируется как $C^2R^{-\alpha^2}$ , что позволяет оценить степень различия между наблюдаемыми и теоретическими распределениями флуктуаций в среде.

Исследование распространения света сквозь случайные пространственно-временные среды, представленное в данной работе, демонстрирует элегантную сложность взаимодействия света и турбулентности. Модель, основанная на стохастических частных дифференциальных уравнениях, раскрывает немарковские характеристики и пространственные корреляции, оказывающие влияние на поведение светового поля. Как однажды заметил Эрвин Шрёдингер: «Всё, что мы можем знать, — это то, что мы знаем». Эта фраза удивительно перекликается с подходом, представленным в исследовании, поскольку авторы стремятся точно определить и смоделировать процессы, происходящие в среде, несмотря на присущую им случайность и сложность. Особенно важен вывод о влиянии корреляций на интенсивность света, что подчеркивает необходимость учитывать эти факторы при создании точных моделей распространения света.

Куда же дальше?

Представленная работа, будучи шагом к более тонкому пониманию распространения света в турбулентных средах, лишь подчеркивает глубину нерешенных вопросов. Элегантность математической модели, конечно, радует глаз, однако реальный мир редко бывает столь послушным. Особый интерес вызывает влияние пространственных корреляций — насколько глубоко “запомнила” среда свое прошлое, и как это влияет на текущее поведение света? Похоже, что предложенная модель лишь слегка приоткрыла дверь в этот сложный лабиринт.

Очевидным направлением дальнейших исследований представляется расширение модели с учетом нелинейных эффектов. Свет, взаимодействуя со средой, сам может её изменять, создавая петли обратной связи. Учитывая, что природа редко терпит одностороннее влияние, пренебрежение этими эффектами кажется, мягко говоря, неоптимальным. Более того, необходимо разработать более эффективные методы валидации модели в условиях, максимально приближенных к реальным — полевые эксперименты, безусловно, важны, но их сложность и стоимость ограничивают возможности для детального анализа.

В конечном итоге, задача заключается не в создании все более сложных математических конструкций, а в достижении глубокого, интуитивного понимания процессов, определяющих поведение света в сложных средах. Подобно искусству, хорошая наука должна быть лаконичной и выразительной — каждая переменная, каждый параметр должен иметь ясный смысл и отражать фундаментальные свойства системы. Беспорядок в коде, как и в физических моделях, рано или поздно дает о себе знать.

Оригинал статьи: https://arxiv.org/pdf/2601.11213.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-21 08:13