Сплетение и распространение: новая картина запутанности в цепях фермионов

Автор: Денис Аветисян

Исследование аналитически раскрывает структуру запутанности и динамику операторов в слабо взаимодействующих цепях Майораны, выявляя ключевую роль ‘мембраны запутанности’.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал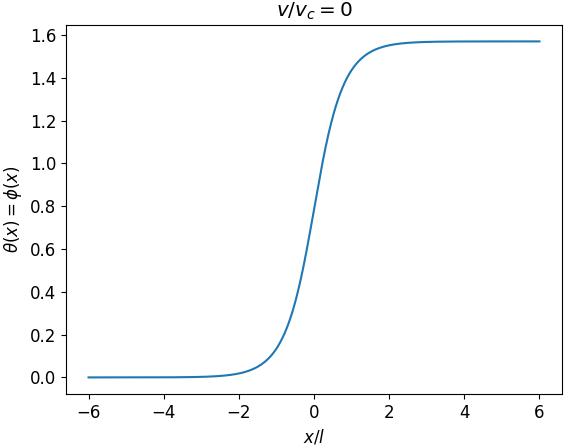

Решение уравнений движения при <span class="katex-eq" data-katex-display="false">\theta(x) = \phi(x)</span> определяет скорость роста запутанности состояний после скачка из слабозапутанного состояния, а также напряжение мембраны запутанности <span class="katex-eq" data-katex-display="false">\mathcal{E}(v)</span> при <span class="katex-eq" data-katex-display="false">v=0</span>; точное непрерывное представление границы описывается как <span class="katex-eq" data-katex-display="false">\theta(x) = \arctan\exp\left(2x/l\right)</span> (уравнение 35), причём данное решение демонстрирует вырожденность относительно пространственных сдвигов, где <span class="katex-eq" data-katex-display="false">l \equiv \Delta\_0 / \Delta\_I</span>. — Решение уравнений движения при $\theta(x) = \phi(x)$ определяет скорость роста запутанности состояний после скачка из слабозапутанного состояния, а также напряжение мембраны запутанности $\mathcal{E}(v)$ при $v=0$ ; точное непрерывное представление границы описывается как $\theta(x) = \arctan\exp\left(2x/l\right)$ (уравнение 35), причём данное решение демонстрирует вырожденность относительно пространственных сдвигов, где $l \equiv \Delta\_0 / \Delta\_I$ .

Работа посвящена аналитическому исследованию структуры запутанности и динамики операторов в слабо взаимодействующих цепях фермионов, демонстрируя возникновение ‘мембраны запутанности’ с характерным напряжением и определяя скорость ‘бабочки’ как критическую скорость для баллистического распространения.

Несмотря на прогресс в понимании запутанности в кванетных системах, описание динамики информации в реалистичных, зашумленных системах остается сложной задачей. В работе ‘Continuum mechanics of entanglement in noisy interacting fermion chains’ разработан континуальный подход к изучению распространения информации в цепи взаимодействующих майорановских фермионов. Показано, что в пределе слабых взаимодействий возникает «мембрана запутанности» — связанное состояние двух волн, характеризующееся определенным натяжением, а скорость этой мембраны стремится к так называемой «скорости бабочки». Каким образом этот формализм может быть расширен для описания более сильных взаимодействий и не-фермионных систем, и какие новые физические явления он может предсказать?

Квантовая Спутанность: Границы Нелокальности

Понимание распространения квантовой запутанности имеет первостепенное значение для характеристики квантовых систем, состоящих из множества частиц, однако непосредственное наблюдение этого процесса представляет собой серьезную научную задачу. Запутанность — это нелокальная корреляция между частицами, которая позволяет им сохранять связь даже на больших расстояниях, и ее динамика определяет многие свойства системы. Трудность заключается в том, что измерение запутанности требует точного контроля над всеми частицами системы и исключения влияния внешних факторов. Кроме того, в сложных системах, состоящих из большого числа частиц, запутанность может быстро разрушаться из-за взаимодействий с окружающей средой или внутренних процессов. Разработка новых методов для отслеживания и измерения распространения запутанности позволит глубже понять природу квантовых явлений и открыть новые возможности для квантовых технологий, включая квантовые вычисления и квантовую связь.

Традиционные методы исследования квантовой запутанности сталкиваются с серьезными трудностями в системах с беспорядком, где взаимодействия между частицами слабы, а дальнодействующие корреляции играют определяющую роль. В таких системах, где локальные возмущения могут значительно влиять на глобальное квантовое состояние, стандартные подходы, основанные на упрощенных моделях или анализе близких взаимодействий, оказываются неэффективными. Неспособность адекватно описать сложные корреляции, возникающие из-за слабости связей и случайного распределения параметров системы, приводит к неточным результатам и затрудняет понимание фундаментальных процессов, происходящих в материалах с беспорядком. Поэтому, для эффективного изучения квантовых явлений в подобных системах требуется разработка принципиально новых теоретических инструментов и экспериментальных методов, способных учитывать сложность и нелокальность взаимодействий.

Исследование слабо взаимодействующей цепочки Майораны представляет собой перспективный подход к изучению динамики запутанности и, одновременно, предоставляет платформу для разработки топологических квантовых вычислений. Данные цепочки, состоящие из частиц, являющихся собственными античастицами, демонстрируют уникальные свойства, защищающие квантовую информацию от декогеренции — основного препятствия на пути создания стабильных кубитов. В рамках данной работы ученые стремятся отследить, как запутанность распространяется вдоль цепочки Майораны, учитывая слабое взаимодействие между частицами и влияние случайных возмущений. Понимание этих процессов критически важно не только для характеристики квантовых многотельных систем, но и для создания надежных квантовых устройств, способных выполнять сложные вычисления.

Для адекватного описания динамики запутанности в сложных квантовых системах, таких как цепочки Майораны, необходима разработка теоретической базы, способной учитывать их внутреннюю сложность и тонкое взаимодействие между взаимодействиями между частицами и случайными отклонениями в системе. Такая база должна выходить за рамки стандартных приближений, которые часто оказываются неэффективными в условиях слабого взаимодействия и дальнодействующих корреляций. Она требует учета нелинейных эффектов и влияния беспорядка на распространение запутанности, что предполагает использование продвинутых математических методов и вычислительных алгоритмов для моделирования и анализа поведения системы. Разработка подобного подхода открывает новые возможности для понимания и контроля квантовых систем, перспективных для топологических квантовых вычислений и других передовых технологий.

Репликальный Трюк и Интегралы по Траекториям: Инструменты Квантового Анализа

В основе нашего анализа лежит метод реплик, позволяющий преобразовать задачу вычисления запутанности в более решаемую классическую задачу. Этот подход предполагает рассмотрение $n$ -кратных реплик рассматриваемой системы, где $n$ — целое число. Затем вычисляется функция разделения для реплицированной системы, а результат экстраполируется в пределе $n \rightarrow 1$ . Данная процедура позволяет связать энтропию запутанности с корреляционными функциями реплицированной системы, что упрощает вычисления и позволяет избежать прямого обращения к сложным квантовым вычислениям, характерным для непосредственного вычисления энтропии запутанности.

Формулировка интеграла по траекториям в представлении когерентных состояний является мощным инструментом для описания квантовой динамики системы. В этом формализме, переменными интегрирования выступают когерентные состояния, что позволяет представить квантовую эволюцию как функциональный интеграл по этим состояниям. Такой подход особенно полезен при анализе систем с большим числом частиц, где традиционные методы могут оказаться неэффективными. Использование когерентных состояний позволяет упростить вычисления, представляя квантовые операторы в виде классических функций от этих состояний и позволяя применять методы классической статистики для оценки соответствующих функциональных интегралов. $\in t \mathcal{D}\alpha e^{iS[\alpha]}$ , где $S[\alpha]$ — действие, выраженное через когерентные состояния α.

Методы, включающие трюк с репликами и интегралы по траекториям, критически важны для исследования многочастичной запутанности. Анализ запутанности в системах с большим количеством частиц представляет собой вычислительно сложную задачу, поскольку количество возможных состояний экспоненциально растет. Эти методы позволяют обойти ограничения традиционных возмущающих подходов и эффективно рассчитывать энтропию запутанности и другие ключевые характеристики, предоставляя возможность извлекать значимые физические выводы о корреляциях между частицами и фазовых переходах в конденсированных средах и квантовых системах. Полученные данные используются для характеризации квантовых состояний вещества и понимания фундаментальных свойств сложных квантовых систем.

Традиционные возмущающие методы в квантовой теории сталкиваются со значительными трудностями при анализе сильнокоррелированных систем, где взаимодействие между частицами превосходит кинетическую энергию. Использование репликального трюка и интегралов по траекториям позволяет обойти эти ограничения, поскольку эти методы не полагаются на малое возмущение. Вместо этого, они позволяют выразить энтропию запутанности через классические вычисления, избегая расходимостей и неточностей, характерных для пертурбативных подходов, особенно в системах с большим количеством частиц и сложными корреляциями. Это особенно важно для исследования квантовых фазовых переходов и свойств конденсированных сред, где корреляции играют определяющую роль.

При увеличении скорости от <span class="katex-eq" data-katex-display="false">v/v_c = 0.2</span> до <span class="katex-eq" data-katex-display="false">v/v_c = 0.9</span> происходит переход от значительного перекрытия доменных стенок в θ и φ к их практически независимому распространению, что демонстрирует изменение взаимодействия между ними при различных скоростях, рассчитанное численно при <span class="katex-eq" data-katex-display="false">K = \Delta_I/\Delta_0 = 0.01</span>. — При увеличении скорости от $v/v_c = 0.2$ до $v/v_c = 0.9$ происходит переход от значительного перекрытия доменных стенок в θ и φ к их практически независимому распространению, что демонстрирует изменение взаимодействия между ними при различных скоростях, рассчитанное численно при $K = \Delta_I/\Delta_0 = 0.01$ .

Седловое Приближение и Мембрана Запутанности: Волновой Фронт Корреляций

Применение метода седловых точек к интегралу по траекториям выявило связь с уравнением Фишера-КПП, известным уравнением для распространения бегущей волны. Данное уравнение описывает эволюцию фронта волны и широко используется в различных областях физики и биологии, включая теорию горения, распространение популяций и, в данном контексте, распространение запутанности. Уравнение Фишера-КПП имеет вид $\frac{\partial u}{\partial t} = D\frac{\partial^2 u}{\partial x^2} + u(1-u)$ , где $u(x,t)$ представляет собой плотность фронта волны, а $D$ — коэффициент диффузии. Установление этой связи позволяет интерпретировать динамику запутанности в терминах волнового процесса, где фронт волны соответствует границе области запутанности.

Применение седлового приближения к интегралу по траекториям выявило связь с уравнением Фишера-КПП, известным уравнением для распространения волн. Это указывает на то, что запутанность распространяется подобно волне, формируя структуру, которую мы определяем как ‘мембрана запутанности’. Данная мембрана не является физической границей, а представляет собой фронт распространения корреляций между квантовыми степенями свободы системы. Скорость распространения запутанности вдоль этой мембраны определяется критической скоростью $vc = 16\sqrt{2}\Delta_0\Delta_I$ , где $\Delta_0$ и $\Delta_I$ являются параметрами, характеризующими начальное состояние и взаимодействие в системе, соответственно.

Напряжение, возникающее в формирующейся ‘мембране запутанности’, напрямую связано со скоростью распространения запутанности в системе. Данная связь позволяет характеризовать скорость распространения запутанности через физическое свойство мембраны — ее натяжение. В наших расчетах критическая скорость, определяющая данное распространение, выражается как $vc = 16\sqrt{2}\Delta_0\Delta_I$ , где $\Delta_0$ и $\Delta_I$ являются параметрами, характеризующими начальную запутанность и взаимодействие соответственно. Таким образом, натяжение мембраны служит мерой сопротивления ее деформации, вызванной распространением запутанности, и, следовательно, определяет скорость этого процесса.

Наши расчеты, подтвержденные анализом коррелятора, не упорядоченного по времени (OTOC), демонстрируют механизм распространения и установления равновесия запутанности. Установлено, что критическая скорость, определяемая как $v_c = 16\sqrt{2}\Delta_0\Delta_I$ , является определяющим фактором для данной динамики. Здесь, $\Delta_0$ и $\Delta_I$ представляют собой соответствующие параметры, характеризующие начальную и конечную точки распространения запутанности, и скорость $v_c$ определяет максимальную скорость, с которой запутанность может эффективно распространяться в системе.

При численном решении для <span class="katex-eq" data-katex-display="false">K \equiv \Delta_{I}/\Delta_{0} = 0.01</span>, наблюдается пример решения в виде движущейся волны вправо, где точка <span class="katex-eq" data-katex-display="false">x_{mid}</span> выбрана произвольно при условии <span class="katex-eq" data-katex-display="false">\theta = 2\arctan z = \pi/4</span>. — При численном решении для $K \equiv \Delta_{I}/\Delta_{0} = 0.01$ , наблюдается пример решения в виде движущейся волны вправо, где точка $x_{mid}$ выбрана произвольно при условии $\theta = 2\arctan z = \pi/4$ .

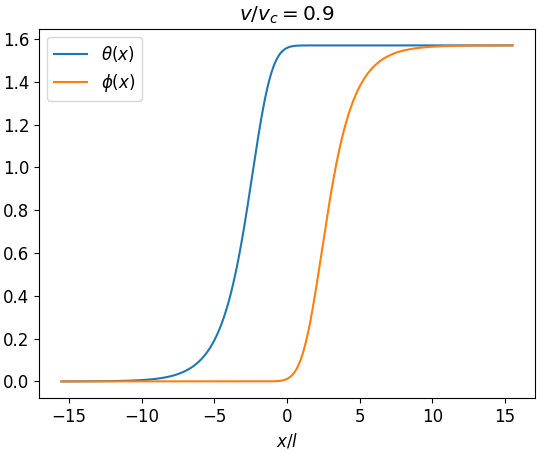
Скорость Бабочки и Критические Явления: Понимание Границы Хаоса

Исследование выявило ключевую роль так называемой “скорости бабочки” — скорости распространения малых возмущений — в определении поведения “спутанной мембраны”. Данный параметр, характеризующий скорость, с которой незначительные изменения в системе могут привести к значительным последствиям, оказался фундаментальным для понимания динамики квантовой запутанности. Установлено, что именно скорость бабочки определяет стабильность и структуру этой мембраны, оказывая влияние на ее способность поддерживать квантовые связи. Изучение этого параметра позволяет получить новые представления о механизмах распространения информации в сложных квантовых системах и о том, как локальные возмущения могут влиять на глобальное поведение всей системы. $v_B$ является определяющим фактором в исследовании критических явлений и динамики запутанности.

Исследование выявило тесную связь между так называемой «скоростью бабочки» — параметром, определяющим скорость распространения малых возмущений — и «критической скоростью», обозначающей переход между различными динамическими режимами системы. Установлено, что критическая скорость, определяющая этот переход, выражается формулой $v_c = 16\sqrt{2}\Delta_0\Delta_I$ , где $\Delta_0$ и $\Delta_I$ представляют собой ключевые параметры, характеризующие свойства системы. Это открытие позволяет понять, как небольшие изменения в начальных условиях могут приводить к кардинальным перестройкам в динамике системы, а также предоставляет инструмент для предсказания моментов возникновения критических переходов и связанных с ними явлений.

Исследования, основанные на описании OTOC посредством марковского процесса, выявили прямую пропорциональность между натяжением так называемой «мембраны запутанности» и скоростью распространения малых возмущений. Установлено, что натяжение этой мембраны, определяющее её устойчивость и динамические свойства, неразрывно связано с $vc = 16\sqrt{2}\Delta_0\Delta_I$ , скоростью, характеризующей критический переход между различными режимами поведения системы. Данная зависимость указывает на фундаментальную связь между распространением информации, степенью запутанности квантовых состояний и критическими явлениями, позволяя лучше понять внутреннюю структуру и динамику сложных квантовых систем, где мембрана запутанности играет роль ключевого элемента, определяющего их поведение.

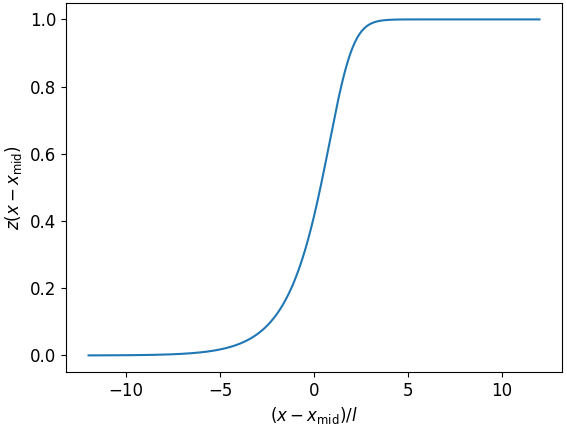
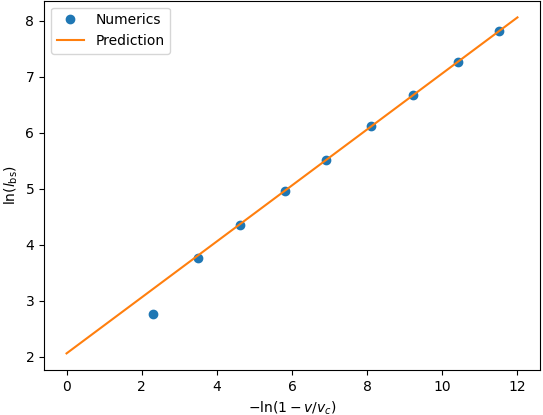
Исследование выявило универсальную функцию масштабирования, $g(v/vc)$ , определяющую поведение «связанной мембраны» — структуры, возникающей из квантовой запутанности. Было показано, что размер этой связанной области неограниченно возрастает, приближаясь к критической скорости $vc$ , что математически выражается как $lbs ~ 1/\sqrt(1 - |v|/vc)$ . Данный результат предоставляет принципиально новый подход к пониманию взаимосвязи между квантовой запутанностью, скоростью распространения информации и критическими явлениями в квантовых системах, позволяя описывать их в рамках единой, масштабно-инвариантной модели.

Численное исследование с использованием итеративного метода подтверждает предсказание формулы (46) о зависимости размера связанного состояния <span class="katex-eq" data-katex-display="false">l_{bs}</span> от величины <span class="katex-eq" data-katex-display="false">1-v/v_c</span> при приближении <span class="katex-eq" data-katex-display="false">v</span> к <span class="katex-eq" data-katex-display="false">v_c</span>, при этом для достижения наилучшего соответствия с асимптотическим поведением введено одно подгоночное постоянное смещение при <span class="katex-eq" data-katex-display="false">\Delta I / \Delta_0 = 0.1</span>. — Численное исследование с использованием итеративного метода подтверждает предсказание формулы (46) о зависимости размера связанного состояния $l_{bs}$ от величины $1-v/v_c$ при приближении $v$ к $v_c$ , при этом для достижения наилучшего соответствия с асимптотическим поведением введено одно подгоночное постоянное смещение при $\Delta I / \Delta_0 = 0.1$ .

Исследование показывает, что даже в кажущейся простоте взаимодействующих цепочек майорановских фермионов формируется сложная структура — своего рода ‘мембрана запутанности’. Это напоминает о хрупкости любой системы, о ее склонности к компромиссам. Как пишет Ханна Арендт: «Политика рождается из действия, а не из идеи». Точно так же и данная работа демонстрирует, что фундаментальные свойства системы проявляются не в абстрактных моделях, а в динамике распространения операторов и в конечном итоге — в скорости ‘бабочки’. Стремление к точности, к идеальному описанию, часто игнорирует неизбежный шум и взаимодействие, которые и определяют реальное поведение системы. Архитектура здесь — это не структура, а компромисс, застывший во времени.

Куда Ведет Этот Хаос?

Представленная работа, исследуя механику запутанности в слабо взаимодействующих фермионных цепях, лишь приоткрывает завесу над сложной динамикой нелокальных корреляций. Понятие “мембраны запутанности” — не столько архитектурный элемент, сколько эмерджентное свойство системы, возникающее из тонкого баланса между когерентностью и декогеренцией. Очевидно, что стремление к точным решениям — это всего лишь попытка договориться с вероятностью, ведь гарантии стабильности — иллюзия, умело закэшированная в приближениях.

Следующим шагом представляется не поиск “идеальной” модели, а исследование поведения этой мембраны в условиях сильных возмущений и неоднородностей. “Скорость бабочки” — лишь один из параметров, определяющих скорость распространения информации, но игнорировать нелинейные эффекты и возможность возникновения самоорганизующихся структур было бы наивно. Хаос — не сбой, а язык природы, и задача исследователя — научиться его понимать, а не подавлять.

В конечном итоге, истинная сложность заключается не в аналитическом описании конкретных систем, а в понимании общих принципов, управляющих эмерджентными свойствами материи. Попытки построить “идеальную” систему обречены на провал; гораздо перспективнее — научиться выращивать экосистемы, способные адаптироваться к меняющимся условиям и порождать новые формы порядка из хаоса.

Оригинал статьи: https://arxiv.org/pdf/2601.21134.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-31 20:52