Автор: Денис Аветисян
Исследование предлагает переосмысление взаимодействия ультракоротких оптических импульсов с прозрачными проводящими оксидами, выявляя ключевую роль поглощения в формировании отклика.
Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.
Бесплатный телеграм-канал
Разработана квантово-оптическая теория, использующая энергетическое представление уравнений Максвелла-Блоха для моделирования динамики электронов в металлах с непараболической зоной проводимости.
Несмотря на значительный прогресс в нелинейной оптике, адекватное описание взаимодействия сверхкоротких оптических импульсов с проводящими оксидами остается сложной задачей. В данной работе, посвященной ‘Quantum-optical theory of the few femtosecond nonlinear optical response of Drude metals with a non-parabolic conduction band’, разработана энерго-пространственная формулировка уравнений Максвелла-Блоха для моделирования этого взаимодействия. Показано, что в режиме интенсивного возбуждения поглощение превалирует над излучением, а существенный вклад в нелинейный отклик вносит поглощение в возбужденные состояния. Каким образом предложенный подход может быть расширен для описания более сложных материалов и режимов возбуждения, включая когерентные эффекты?
За пределами линейности: Ограничения традиционного моделирования
Исследование взаимодействия света с веществом в материалах, таких как оксид индия-олова (ITO), неизбежно сталкивается с выраженными нелинейностями, которые существенно усложняют процесс моделирования. В отличие от линейных систем, где отклик пропорционален воздействию, в нелинейных материалах возникают сложные гармонические искажения и другие эффекты, требующие учета высокопорядковых членов в уравнениях. Это, в свою очередь, ведет к экспоненциальному росту вычислительных затрат, поскольку для адекватного описания нелинейного отклика необходимо учитывать взаимодействие множества фотонов с электронами материала и решать сложные системы дифференциальных уравнений. В результате, моделирование даже относительно небольших систем может потребовать значительных вычислительных ресурсов и времени, представляя собой серьезную проблему для разработки и оптимизации оптических устройств на основе подобных материалов. E = E_0 + \chi^{(2)}E^2 + \chi^{(3)}E^3 — пример нелинейного отклика, где \chi^{(2)} и \chi^{(3)} — нелинейные восприимчивости.
Традиционные методы, такие как Теория функционала плотности во временной зависимости (TDDFT), сталкиваются с серьезными вычислительными ограничениями при моделировании сложных явлений в материалах, например, при исследовании взаимодействия света с веществом в оксиде олова и индия (ITO). Сложность заключается в экспоненциальном росте вычислительных затрат с увеличением числа частиц и необходимостью точного учета нелинейных эффектов. Для адекватного описания этих явлений требуется учет множества электронных взаимодействий, что приводит к увеличению требуемой памяти и времени вычислений. В результате, применение TDDFT для больших систем или длительных временных интервалов становится практически невозможным, что затрудняет разработку и оптимизацию передовых оптических устройств на основе подобных материалов.
Точная модель поведения материалов, таких как оксид индия-олова (ITO), имеет первостепенное значение для разработки и оптимизации передовых оптических устройств. Нелинейные оптические свойства этих материалов определяют их эффективность в таких приложениях, как высокоскоростные модуляторы света, оптические переключатели и сенсоры. Улучшенное понимание и точное моделирование этих свойств позволяют инженерам настраивать состав и структуру материалов для достижения желаемых оптических характеристик, таких как повышенная нелинейность или сниженные потери. В конечном итоге, возможность предсказывать и контролировать оптическое поведение ITO и подобных материалов открывает путь к созданию более компактных, эффективных и функциональных оптических устройств нового поколения, необходимых для развития телекоммуникаций, обработки информации и других технологических областей.
Энергетический ландшафт: Вычислительная стратегия
Формулировка в энергетическом пространстве (Energy-Space Formulation) представляет собой существенное упрощение вычислительных задач за счет преобразования расчетов из импульсного пространства в энергетическое. Традиционно, моделирование динамики электронов требует учета импульса каждой частицы, что приводит к экспоненциальному росту вычислительной сложности с увеличением числа частиц. Переход к энергетическому пространству позволяет описывать состояния электронов через их энергию E и другие соответствующие квантовые числа, что снижает размерность решаемых задач и, следовательно, вычислительные затраты. Вместо решения уравнений, зависящих от импульса \vec{k}, рассматриваются уравнения, зависящие от энергии E, что особенно эффективно при моделировании систем с большим числом частиц или в задачах, где важны энергетические уровни и переходы.
Интеграция энергетического подхода с формализмом Максвелла-Блоха обеспечивает отслеживание динамики электронных состояний со значительно сниженными вычислительными затратами. В отличие от традиционных расчетов в импульсном пространстве, данный метод позволяет уменьшить вычислительную сложность за счет фокусировки на энергетически-разрешенных взаимодействиях. Это достигается путем описания эволюции поляризации среды и динамики электронов в энергетическом пространстве, что снижает требования к ресурсам и времени вычислений, особенно при моделировании сложных систем и процессов взаимодействия света с веществом. \frac{\partial}{\partial t} \rho = -i[\hat{H}, \rho] описывает эволюцию матрицы плотности ρ под действием гамильтониана \hat{H} .
Переход к рассмотрению взаимодействий, разрешенных по энергии, позволяет получить более четкое представление о фундаментальных физических процессах, лежащих в основе взаимодействия света с веществом. Традиционно анализ часто проводился в импульсном пространстве, однако учет энергии взаимодействия \hbar \omega непосредственно связывает процессы с конкретными энергетическими уровнями системы. Это позволяет более точно моделировать явления, такие как поглощение, излучение и рассеяние фотонов, а также отслеживать переходы между энергетическими состояниями электронов. Идентифицируя и анализируя эти энергетически-зависимые взаимодействия, можно получить детальную информацию о динамике и механизмах, определяющих отклик материала на внешнее электромагнитное излучение.
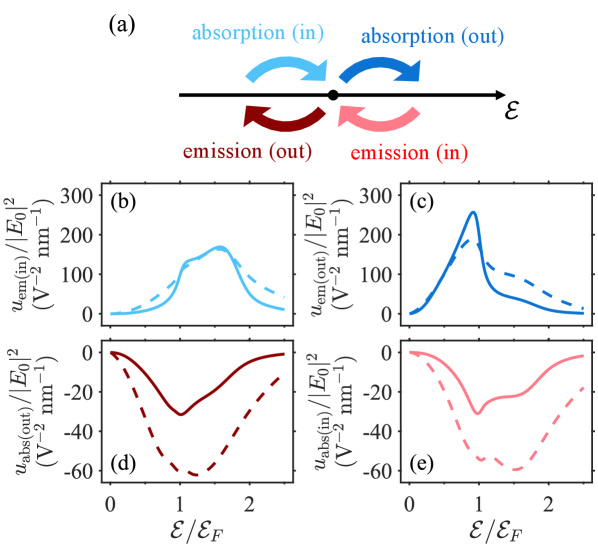
Расшифровка отклика: Электронные взаимодействия и оптические эффекты
Взаимодействие фотонов с электронами в оксиде индия-олова (ITO) происходит посредством нескольких процессов рассеяния. К ним относятся столкновения электронов с фононами (колебаниями кристаллической решетки), приводящие к потере энергии и изменению направления движения электронов; столкновения с примесями, которые являются дефектами в кристаллической структуре и также изменяют траекторию электронов; и столкновения между самими электронами, обусловленные кулоновским взаимодействием. Интенсивность каждого из этих процессов зависит от температуры, концентрации примесей и плотности носителей заряда в материале, определяя общую динамику релаксации возбужденных электронов и, как следствие, оптические свойства ITO.
Столкновения электронов с фононами, примесями и другими электронами в оксиде индия-олова (ITO) оказывают существенное влияние на динамику релаксации возбужденных электронов. Процесс релаксации, включающий потерю энергии возбужденными электронами посредством этих столкновений, определяет время жизни возбужденного состояния. Более короткое время жизни, вызванное более частыми столкновениями, приводит к уширению спектральных линий и снижению эффективности стимулированного излучения. В частности, увеличение частоты столкновений уменьшает вероятность когерентного излучения и способствует нерадиационным процессам рекомбинации, что напрямую влияет на характеристики поглощения и стимулированного излучения материала, определяя его оптические свойства.
Модель Друде предоставляет адекватное описание поведения электронов в оксиде индия-олова (ITO), рассматривая их как свободные электроны, сталкивающиеся с ионизированными примесями. В рамках данной модели, электроны подвержены столкновениям, определяющим среднюю длину свободного пробега и время релаксации, что напрямую влияет на электропроводность и оптические свойства материала. В частности, модель позволяет рассчитать частотную зависимость диэлектрической проницаемости \epsilon(\omega) и объяснить наблюдаемые явления, такие как поглощение света в инфракрасном диапазоне и отражающую способность ITO. Хотя модель Друде является упрощением реальной картины, она служит фундаментальной основой для понимания и прогнозирования макроскопического оптического отклика ITO, особенно в контексте разработки прозрачных проводящих электродов.
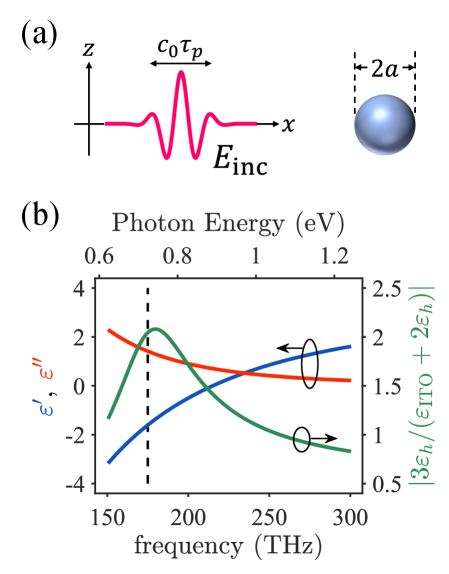
Наноконтроль: Локальные поля и усиленная нелинейность
Геометрия наносферы оксида индия-олова (ITO) играет ключевую роль в усилении локальных электромагнитных полей. Благодаря специфической форме и размерам наночастицы, падающее электромагнитное излучение концентрируется вблизи поверхности, что приводит к значительному увеличению амплитуды электрического поля. Этот эффект, известный как усиление локального поля, существенно повышает взаимодействие света с электронами в материале. Фактически, взаимодействие света и электронов становится более интенсивным из-за концентрации энергии, что открывает возможности для управления оптическими свойствами материала на наноуровне и позволяет создавать устройства с повышенной чувствительностью и эффективностью. Усиление локального поля особенно важно в контексте нелинейной оптики, поскольку оно пропорционально четвертой степени напряженности электрического поля, что делает даже слабые нелинейные эффекты заметными и применимыми.
Уникальное сочетание усиления локальных полей и характеристик ITO, близких к так называемой «эпсилон-близкой к нулю» (ENZ), приводит к резкому увеличению нелинейной оптической восприимчивости материала. Вблизи ENZ-частоты диэлектрическая проницаемость ITO стремится к нулю, что существенно изменяет взаимодействие света с электронами в материале. Это приводит к концентрации электромагнитного поля вокруг наночастиц, усиливая нелинейные оптические эффекты, такие как генерация гармоник и нелинейное поглощение. Именно данное сочетание позволяет добиться значительно более сильных нелинейных откликов по сравнению с другими материалами, открывая возможности для создания компактных и эффективных оптических устройств.
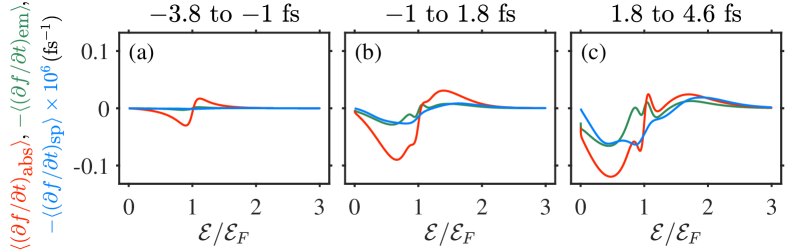
Исследование выявило, что поглощение света в наноструктурах оксида индия-олова демонстрирует сверхлинейную зависимость от интенсивности возбуждения, что обусловлено эффектами в возбужденных состояниях материала. Этот феномен указывает на нелинейное взаимодействие света с электронами, значительно превосходящее линейное поглощение. При этом, скорость спонтанного излучения оказалась приблизительно в 106 раз ниже, чем скорости вынужденного излучения и поглощения. Такое существенное различие свидетельствует о доминировании когерентных процессов над спонтанными, что открывает перспективы для создания эффективных оптических устройств с контролируемыми характеристиками излучения и поглощения.
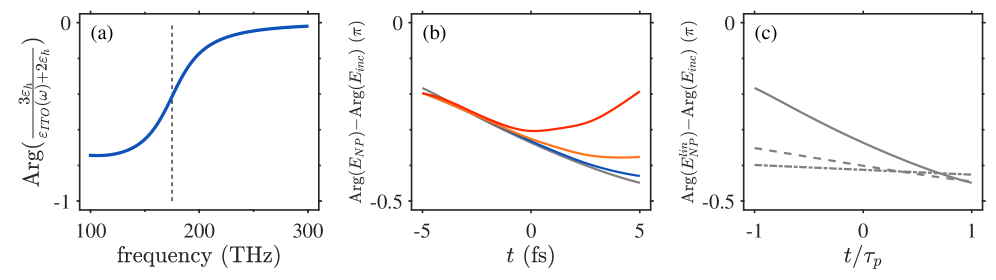
Исследование взаимодействия ультракоротких импульсов с прозрачными проводящими оксидами демонстрирует сложность описания динамики электронов в металлах. Представленная в работе формулировка уравнений Максвелла-Блоха в энергетическом пространстве позволяет увидеть преобладание процессов поглощения над излучением, что подчеркивает важность рассмотрения поглощения в возбужденных состояниях. Как однажды заметил Игорь Тамм: «В науке нет ничего окончательного, все всегда можно пересмотреть». Эта фраза особенно актуальна в контексте данной работы, ведь любое упрощение в моделировании сложных систем, таких как прозрачные проводящие оксиды, несет в себе риск упустить важные детали, способные раствориться в горизонте событий нашего понимания.
Что дальше?
Представленная работа, как и многие другие, исследует взаимодействие света и материи в рамках, казалось бы, установленных закономерностей. Однако, каждый новый подход к моделированию отклика прозрачных проводящих оксидов, каждый изысканный учёт непараболической зоны проводимости, лишь подчеркивает фундаментальную сложность описываемых процессов. Преобладание поглощения над излучением, выявленное в данной работе, не является чем-то принципиально новым, но служит очередным напоминанием о том, что «простота» — это иллюзия, а «элегантно» — часто лишь удобство расчётов.
Будущие исследования, вероятно, будут направлены на усложнение модели, включение новых эффектов, учёт взаимодействия электронов друг с другом и с решёткой кристалла. Но не стоит ли задаться вопросом, не ведёт ли нас это к бесконечному циклу усложнения, где каждая добавленная деталь лишь порождает новые вопросы? Каждая новая попытка «приблизить» модель к реальности рискует лишь глубже погрузить в пучину неизвестного, где горизонт событий, как и в случае чёрной дыры, становится всё более далёким.
В конечном итоге, истинным прогрессом станет не создание всё более сложных моделей, а развитие методов, позволяющих отделить существенное от несущественного, выявить универсальные закономерности, которые не зависят от конкретных деталей системы. Иначе, каждое новое предположение о сингулярности, каким бы изящным оно ни было, останется лишь ещё одним эхом в безмолвном космосе.
Оригинал статьи: https://arxiv.org/pdf/2601.10985.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Все рецепты культистского круга в Escape from Tarkov
- Решение головоломки с паролем Absolum в Yeldrim.
- Лучшие транспортные средства в Far Cry 6
- Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip
- Репозиторий: Как исправить таймаут клиента
- Кто такая Кселия Мендес-Джонс? 5 вещей, которые нужно знать об актере Fallout
- Jujutsu Kaisen Modulo Глава 18: Предварительный просмотр: Полная мощь Рики и Цуруги.
- В стороне: QB и я В ролях: каждый актер, который появляется (фотографии)
- Лучшие шаблоны дивизий в Hearts Of Iron 4
- Акции UGLD. Южуралзолото ГК: прогноз акций.
2026-01-19 21:12