Автор: Денис Аветисян
Новое исследование раскрывает, что возникновение магнетизма под воздействием света обусловлено фундаментальными свойствами квантовой геометрии электронных систем.
Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.
Бесплатный телеграм-канал
Работа демонстрирует, что инверсные эффекты Фарадея и Коттона-Маутона объединяются через квадрупольный момент квантовой метрики и взвешенную квантовую метрику, описываемые с помощью уравнения Больцмана.
Несмотря на значительный прогресс в понимании магнето-оптических явлений, механизмы, лежащие в основе обратных эффектов Фарадея и Коттона-Мутона, оставались недостаточно изученными. В статье ‘Light-induced Magnetization by Quantum Geometry’ предложен новый подход к объяснению этих эффектов, основанный на квантовой геометрии электронных систем. Показано, что индуцированная светом намагниченность обусловлена квантометрическим квадруполем и взвешенной квантометрикой, обеспечивая единую теорию для обоих обратных эффектов. Может ли предложенный механизм открыть новые пути к управлению магнитными свойствами материалов посредством воздействия света?
Квантовая геометрия: За пределами традиционного понимания
Традиционные модели транспортных явлений, опирающиеся на понятие кривизны Берри \mathcal{B} , долгое время служили основой для понимания движения электронов в кристаллах. Однако, современные исследования демонстрируют, что эти модели не всегда способны адекватно описать сложные взаимодействия между светом и веществом. Кривизна Берри, хотя и важна для объяснения аномального эффекта Холла и других явлений, является лишь частью более широкой картины. Не учитывая тонкости, связанные с геометрическими свойствами волновых функций, в частности, квантовой метрикой g_{\mu\nu} , существующие теории оказываются неполными, не позволяя в полной мере раскрыть потенциал управления электронными свойствами материалов и разработки новых оптоэлектронных устройств. Понимание этих ограничений стимулирует поиск новых теоретических подходов, выходящих за рамки стандартных представлений о транспортных явлениях.
Более глубокое изучение внутренних геометрических свойств квантовых состояний — Квантовой Геометрии — открывает ранее скрытые механизмы, определяющие поведение электронов в материалах. В отличие от традиционных подходов, фокусирующихся исключительно на явлении Берри-кривизны, Квантовая Геометрия учитывает и метрику квантового состояния — тензор, описывающий, как бесконечно малые изменения квантового состояния влияют на его геометрию. Этот подход позволяет понять, что даже при отсутствии Берри-кривизны, электрон может испытывать эффективные силы, обусловленные изменениями метрики. g_{ij} — компоненты этой метрики напрямую связаны с вероятностью перехода между различными квантовыми состояниями, что приводит к новым возможностям управления электронным транспортом и создания устройств с уникальными свойствами. Исследование Квантовой Геометрии позволяет выявить и использовать тонкие геометрические эффекты, которые остаются незамеченными в рамках стандартной теории твердого тела.
Исследование поведения электронов требует учета не только привычной концепции кривизны Берри, но и фундаментальных свойств квантовой геометрии, представленных квантометрикой. Квантометрика, описывающая, как бесконечно малые изменения в квантовом состоянии влияют на расстояние между ними, определяет скорость и характер движения электронов в материале. В то время как кривизна Берри обуславливает аномальные транспортные эффекты, связанные с волновой природой электрона, квантометрика определяет, как легко электрон может перемещаться в пространстве состояний, влияя на его подвижность и рассеяние. Взаимодействие этих двух геометрических величин создает сложную картину, определяющую электронное поведение в различных материалах и открывая возможности для разработки новых электронных устройств с улучшенными характеристиками. Понимание роли квантометрики и ее взаимодействия с кривизной Берри является ключевым для полного описания транспортных явлений и создания материалов с заданными электронными свойствами.
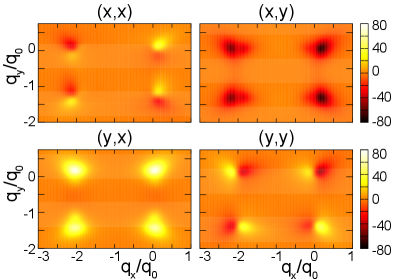
Светоиндуцированная намагниченность: Геометрические корни явления
Эффекты обратного эффекта Фарадея и обратного эффекта Коттона-Маутона демонстрируют возможность индукции намагниченности в материалах под воздействием света. В отличие от традиционных механизмов, где намагниченность является причиной оптических явлений, эти эффекты показывают обратную зависимость — свет является причиной возникновения намагниченности. Наблюдаемые изменения намагниченности пропорциональны интенсивности света и зависят от оптической активности материала, проявляющейся в его способности вращать плоскость поляризации света. Эти эффекты особенно заметны в материалах с высокой нелинейной восприимчивостью и могут быть использованы для создания оптически управляемых магнитных устройств.
Традиционные механизмы, объясняющие намагниченность, индуцированную светом, такие как эффект Фарадея и эффект Коттона-Мутона, оказываются недостаточными для полного описания наблюдаемых явлений. В частности, они не способны предсказать величину и направление намагниченности, возникающей в некоторых материалах под воздействием света. Современные исследования указывают на фундаментальную связь этих эффектов с квантовой геометрией, а именно, с тензорными свойствами, описывающими искривление волновой функции электронов в кристалле. g_{\mu\nu} — взвешенный квантовый метрический тензор и Q_{\mu\nu} — квантовый тензор квадруполя, играют ключевую роль в генерации индуцированной светом намагниченности, определяя ее величину и зависимость от поляризации света и кристаллической структуры материала. Это позволяет предсказывать эффекты, наблюдаемые при определенных условиях симметрии, недоступные для классического подхода.
В процессе генерации светоиндуцированной намагниченности ключевую роль играют взвешенный квантовый метрический тензор g_{ij} и квантовый метрический квадруполь Q_{ijk}. Взвешенный квантовый метрический тензор описывает геометрию волновой функции, а квантовый метрический квадруполь характеризует отклонение этой геометрии от сферической симметрии. Предсказываемые эффекты проявляются при соблюдении определенных условий симметрии материала, в частности, в материалах, не обладающих инвариантностью относительно операций зеркального отражения. Именно эти геометрические характеристики определяют величину и направление светоиндуцированной намагниченности, что позволяет прогнозировать и наблюдать данный эффект в материалах с определенными свойствами кристаллической структуры.
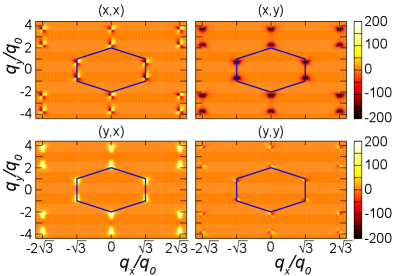
Моделирование токов намагничивания: От теории к предсказаниям
Ток намагничивания, описывающий поток магнитных моментов, может быть вычислен с использованием уравнения Больцмана для переноса и полуклассических уравнений движения. Уравнение Больцмана позволяет описать статистическое поведение носителей заряда (в данном случае, магнитных моментов) под воздействием внешних сил и внутренних процессов рассеяния. Полуклассический подход, в свою очередь, обеспечивает связь между микроскопическими свойствами материалов и их макроскопическим поведением, позволяя рассчитать ток намагничивания на основе кинетических параметров и характеристик рассеяния магнитных моментов. Решение этих уравнений позволяет количественно оценить величину тока намагничивания в различных материалах и предсказать его зависимость от внешних факторов, таких как электрическое поле и температура.
Расчеты, выполненные на основе уравнения Больцмана и полуклассических уравнений движения, показывают, что генерация тока намагничивания обусловлена вкладом взвешенной квантовой метрики и квантового метрического квадруполя под воздействием электрического поля. Прогнозируемые значения тока намагничивания составляют 10^{-{14}} A для циркулярной поляризации (CPL) и 10^{-{13}} A для линейной поляризации (LPL). Данные величины определяются на основе анализа влияния геометрических свойств электронного состояния на динамику магнитных моментов в материале.
Разработанная теоретическая модель учитывает отклонения от стандартной теории переноса, что позволяет более точно описывать поведение магнитных токов в материалах. В отличие от классических подходов, данная модель принимает во внимание квантово-механические эффекты, приводящие к возникновению дополнительных членов в уравнении переноса. Это обеспечивает возможность предсказывать величину и направление магнизационного тока в зависимости от свойств материала и приложенного электрического поля. В результате, модель представляет собой инструмент для целенаправленного проектирования материалов с заданными магнитными характеристиками, что особенно важно для разработки новых типов спинтронных устройств и сенсоров.
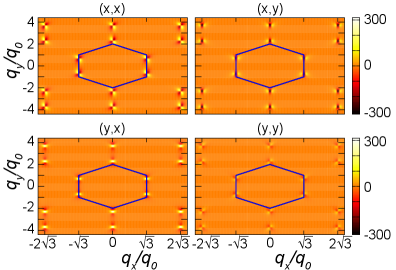
Материальные импликации и вычислительные подходы
Взаимосвязь между структурой материала и индуцированной светом намагниченностью открывает перспективные возможности для создания принципиально новых спинтронных устройств. Исследования показывают, что контролируя микроскопическую организацию вещества — от кристаллической решетки до наличия дефектов — можно эффективно управлять спиновыми токами под воздействием света. Это позволяет разрабатывать компактные и энергоэффективные приборы для хранения и обработки информации, а также создавать сенсоры нового поколения, способные обнаруживать слабые магнитные поля или изменения в оптических свойствах материалов. Подобные устройства, основанные на взаимодействии света и спина, могут стать ключевым элементом будущих технологий, превосходя по своим характеристикам традиционные электронные компоненты и открывая путь к созданию более быстрых, надежных и экономичных систем.
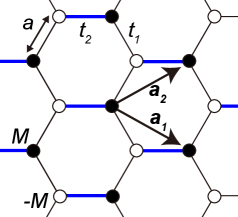
Применение модели плотных связей к материалам с гексагональной решеткой представляет собой перспективный подход к предсказанию и оптимизации светоиндуцированной намагниченности. Данная теоретическая схема позволяет рассчитать электронную структуру и магнитные свойства материалов, учитывая взаимодействие между атомами и влиянием внешнего излучения. E = \sum_{i,j} t_{ij} c_i^\dagger c_j — эта базовая формула описывает переходы электронов между атомами, определяя энергетические уровни и магнитные моменты. Использование модели плотных связей позволяет не только понимать механизмы возникновения намагниченности, но и целенаправленно изменять состав и структуру материалов для достижения заданных характеристик, что открывает новые возможности для создания эффективных спинтронных устройств.
Исследования показывают, что отклонения от вращательной симметрии в структуре материалов оказывают существенное влияние на величину индуцированной светом намагниченности. В частности, даже незначительные асимметрии в расположении атомов кристаллической решетки способны как значительно усиливать, так и подавлять поток намагниченности. Этот эффект открывает принципиально новые возможности для конструирования спинтронных устройств, где асимметрия может выступать в качестве управляющего параметра, позволяя тонко настраивать характеристики устройства и оптимизировать его работу. По сути, контролируя степень отклонения от симметрии, можно эффективно управлять спиновыми токами и создавать материалы с заданными магнитными свойствами, что имеет решающее значение для разработки более эффективных и миниатюрных устройств хранения и обработки информации.
Исследование демонстрирует изящную взаимосвязь между квантовой геометрией и возникновением магнетизации под воздействием света. Подобно тому, как в искусно исполненной мелодии каждый звук имеет значение, здесь квантометрический квадруполь и взвешенная квантометрика оказываются ключевыми элементами, формирующими ответ системы. Авторы предлагают унифицированное объяснение обратных эффектов Фарадея и Коттона-Маутона, подчеркивая, что гармония между формой и функцией в квантовом мире проявляется в тонком балансе геометрических свойств. Как однажды заметила Ханна Арендт: «Политика есть не просто совокупность действий, но и пространство появления нового». В данном исследовании, подобно политике, мы наблюдаем появление нового понимания фундаментальных взаимодействий, где геометрия становится не просто фоном, но и активным участником процесса.
Куда Ведет Свет?
Представленная работа, как и любое глубокое исследование, открывает больше вопросов, чем закрывает. Элегантность объяснения эффектов обратного Фарадея и обратного Коттона-Маутона посредством квантово-геометрических величин не должна заслонять той области нерешенных задач, что простирается перед нами. Понимание роли тензорных свойств квантовой метрики, особенно её квадрупольного момента, требует дальнейшей экспериментальной верификации, а также разработки более точных методов расчета для сложных материалов. Недостаточно просто «услышать» ответ; необходимо настроить каждый интерфейс с вниманием, чтобы понять, как он резонирует с более широкой картиной.
Очевидным следующим шагом представляется исследование влияния взаимодействия между электронами и решеткой на наблюдаемые эффекты. Игнорирование этих взаимодействий — это не просто упрощение; это упущение, которое может исказить истинную природу явления. Более того, необходимо рассмотреть, как квантово-геометрические эффекты проявляются в топологических материалах, где их влияние может быть особенно сильным и приводить к новым, неожиданным эффектам. Плохой дизайн кричит, хороший шепчет, а неверная модель — просто замалчивает.
В конечном итоге, представленная теория может послужить основой для создания новых оптически управляемых устройств. Однако, прежде чем воплотить это в реальность, необходимо понять, как контролировать и оптимизировать квантово-геометрические свойства материалов. И это потребует не только глубоких теоретических знаний, но и значительных усилий в области материаловедения и нанотехнологий. В противном случае, останется лишь еще один красивый, но бесполезный теоретический каркас.
Оригинал статьи: https://arxiv.org/pdf/2601.09637.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Откровенные заметки, слитые стримером Lacari, привели к его бану на Twitch и Kick.
- Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip
- Все рецепты культистского круга в Escape from Tarkov
- Нечестивцам нет покоя: как получить старый ключ от коттеджа
- Решение головоломки с паролем Absolum в Yeldrim.
- Arknights: Endfield — Интерактивная карта (Долина IV)
- Акции UGLD. Южуралзолото ГК: прогноз акций.
- Келли Эллард сейчас: где сегодня убийца под мостом?
- Лучшие шаблоны дивизий в Hearts Of Iron 4
- Кто такая Кселия Мендес-Джонс? 5 вещей, которые нужно знать об актере Fallout
2026-01-16 04:09