Тайны локализации: новые горизонты суперконформных теорий

Автор: Денис Аветисян

Исследование раскрывает неожиданную связь между четырёхмерными калибровочными теориями и двумерной физикой, проливая свет на природу суперконформной симметрии.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал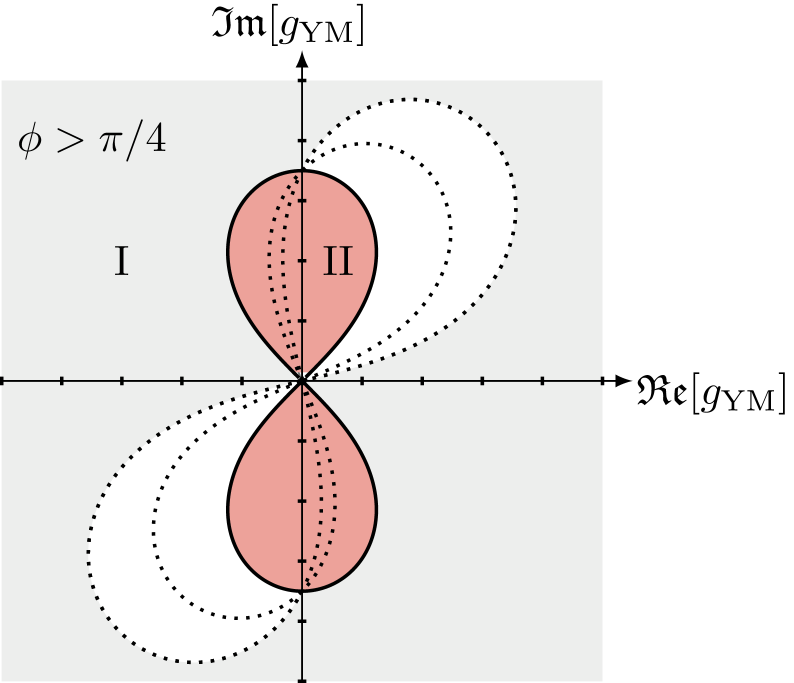

Поворот контура в комплексной плоскости при заданном значении φ приводит к смене области сходимости интеграла, определяющего функцию <span class="katex-eq" data-katex-display="false">\mathcal{Z}(g\_{\text{YM}},\phi)</span>, при этом область расходимости расширяется и вращается, а формальная сумма по остаткам сходится в ограниченной области, напоминающей цифру восемь, что аналогично наблюдается и для функции <span class="katex-eq" data-katex-display="false">\mathcal{Z}\_{\text{ScYM}}(g\_{\text{YM}},\phi)</span> при отражении относительно оси <span class="katex-eq" data-katex-display="false">y</span>. — Поворот контура в комплексной плоскости при заданном значении φ приводит к смене области сходимости интеграла, определяющего функцию $\mathcal{Z}(g\_{\text{YM}},\phi)$ , при этом область расходимости расширяется и вращается, а формальная сумма по остаткам сходится в ограниченной области, напоминающей цифру восемь, что аналогично наблюдается и для функции $\mathcal{Z}\_{\text{ScYM}}(g\_{\text{YM}},\phi)$ при отражении относительно оси $y$ .

В работе показана связь между полюсами в локализованном интеграле по путям 4D теории и неустойчивыми моментами в вложенной 2D калибровочной теории.

Несмотря на успехи метода локализации в изучении конформных калибровочных теорий, аналитическое продолжение соответствующих функционалов часто сталкивается с сингулярностями. В работе «The resurgence of errors in the localization of $\mathcal{N} = 2$ superconformal Yang-Mills» предложена физическая интерпретация этих особенностей, связывающая их с неустойчивыми моментами в двумерной калибровочной теории. Показано, что полюса в локализованном интеграле по траекториям 4D-теории соответствуют именно этим моментам, предлагая двойственное описание физики. Возможно ли дальнейшее развитие этого подхода для решения задач, связанных с непертурбативной динамикой калибровочных полей?

Функция Разделения: Вызов для Невозможного

Функция разделения $Z$ для четырехмерной N=2 суперсимметричной калибровочной теории занимает центральное место в современной теоретической физике, являясь ключевым инструментом для изучения свойств этой теории и ее связей с другими областями, такими как теория струн и математическая физика. Однако, несмотря на свою фундаментальную важность, прямое вычисление этой функции разделения представляет собой чрезвычайно сложную задачу. Интегрируемый характер теории не отменяет экспоненциальный рост сложности при попытке прямого вычисления интеграла по конфигурационному пространству, что делает традиционные методы функционального интегрирования практически неприменимыми. Это обстоятельство обуславливает необходимость разработки инновационных подходов и техник, позволяющих обходить прямые вычисления и находить альтернативные способы определения и анализа этой ключевой величины.

Традиционные методы функционального интегрирования оказываются неэффективными при вычислении $Z$ , функции разделения для четырехмерной N=2 суперсимметричной калибровочной теории. Сложность интегранда, обусловленная нелинейностью и многообразием вкладов от различных полей и конфигураций, приводит к расходимостям и затрудняет получение осмысленных результатов. Это требует разработки принципиально новых подходов к вычислению, таких как локализация и использование топологических свойств теории, позволяющих обойти прямую оценку интеграла и получить точные выражения для $Z$ в определенных условиях. Успех этих инновационных методов демонстрирует возможность преодоления фундаментальных трудностей, возникающих при аналитическом продолжении интегралов в квантовой теории поля.

В области комплексной плоскости, где <span class="katex-eq" data-katex-display="false"> \pi/4 < \text{arg}(a) < 3\pi/4 </span>, интеграл по контуру <span class="katex-eq" data-katex-display="false"> g_{YM} </span> может быть вычислен как сумма вычетов, что иллюстрируется синим контуром. — В области комплексной плоскости, где $\pi/4 < \text{arg}(a) < 3\pi/4$ , интеграл по контуру $g_{YM}$ может быть вычислен как сумма вычетов, что иллюстрируется синим контуром.

Локализация: Путь к Конечному Интегралу

Локализация позволяет свести функциональный интеграл к конечномерному интегралу по пространству модулей калибровочной теории. Вместо вычисления интеграла по бесконечномерному пространству полей, метод локализации использует топологические симметрии и фокусируется на стационарных точках функционала. Это приводит к замене исходного интеграла интегралом по пространству модулей, которое является конечномерным многообразием, параметризующим решения уравнений движения. Такой подход существенно упрощает вычисления и делает возможным аналитическое решение задач, которые в противном случае были бы недоступны.

Локализация позволяет свести вычисление интеграла по траекториям к конечномерному интегралу по пространству модулей калибровочной теории за счет использования топологических симметрий и фокусировки на стационарных точках функционала. Этот подход значительно снижает вычислительные затраты, поскольку вместо интегрирования по всему бесконечномерному пространству функций, вычисление сводится к оценке функционала и его производных в дискретном, конечномерном пространстве. Стационарные точки соответствуют решениям уравнений движения, и фокусировка на них позволяет исключить из рассмотрения все остальные конфигурации, что и обеспечивает существенное уменьшение сложности вычислений.

Ключевым элементом локализованного интеграла являются определители однопетлевых флуктуаций, вычисляемые с использованием сферических гармоник монополей. Эти определители, представляющие собой функциональные интегралы по полям, возникающим вблизи стационарных точек, вносят существенный вклад в окончательное значение интеграла. В частности, сферические гармоники монополей обеспечивают базис для решения уравнений движения вблизи стационарных точек, позволяя вычислить собственные значения оператора, определяющего однопетлевой вклад. Формула для определителя имеет вид $\text{det}(D^\dagger D)$ , где $D$ — оператор, зависящий от геометрии и полей, а вычисление происходит в пространстве, порожденном сферическими гармониками монополей, что значительно упрощает задачу по сравнению с прямым вычислением функционального интеграла.

Раскрытие Сингулярностей: Полюса и Непертурбативные Эффекты

Локализованный интеграл демонстрирует наличие полюсов, что указывает на проявление непертурбативных эффектов в рассматриваемой теории. Эти полюса являются сигналом существования нетривиальных решений, таких как монополи Зейберга-Виттена. Появление полюсов связано с особенностями в комплексной плоскости, возникающими из-за вклада непертурбативных конфигураций, которые не могут быть описаны стандартным разложением в ряд по константе связи. Анализ расположения и остатков этих полюсов позволяет идентифицировать характеристики непертурбативных решений и оценить их вклад в полную физическую картину. Например, положение полюса может быть связано с массой монополя, а остаток — с вероятностью его появления.

Резоргентный анализ предоставляет математический аппарат для изучения аналитической структуры функции разделения, позволяя связать области, описываемые возмущениями (пертурбативными режимами), с областями, где эти возмущения неприменимы (непертурбативными режимами). Этот подход основан на изучении особенностей аналитического продолжения функции разделения, в частности, на анализе полюсов и точек ветвления. Через резоргентное разложение можно получить информацию о непертурбативных эффектах, таких как вкладыды от мгновенных решений и монополей Зейберга-Виттена, которые проявляются как особенности в комплексной плоскости. Суть метода заключается в том, что непертурбативные эффекты представлены в виде асимптотических рядов, которые могут быть реконструированы из информации о сингулярностях функции разделения. $Z = \sum_{k=0}^{\in fty} a_k g^{k} + \sum_{j=0}^{\in fty} b_j e^{-S_j/ \hbar}$ , где $g$ — параметр связи, а $S_j$ — действие непертурбативной конфигурации.

Определение полюсов в локализованном интеграле посредством вычисления вычетов позволяет установить прямую связь между аналитическими особенностями и непертурбативными объектами. В частности, каждое такое полюсное поведение соответствует конкретному решению, представляющему собой монополь Зейберга-Виттена или неустойчивый инстант. Вычет в точке полюса количественно определяет вклад данного непертурбативного решения в общую сумму, определяющую аналитическое продолжение функции раздела. Идентификация этих полюсов и соответствующих им вычетов является ключевым шагом в изучении непертурбативной структуры теории и позволяет вычислить вклад непертурбативных эффектов в различные физические величины. $Z = \sum_{k} N_k e^{-S_k}$ , где $N_k$ — вклад k-го решения, а $S_k$ — его действие.

Двумерное Эхо: Отображение в Более Простую Теорию

В рамках изучения теории Янга-Миллса, обнаружено, что описание четырехмерной теории возможно посредством эквивалентной двухмерной модели. Это достигается за счет использования функции разделения двухмерной теории, которая, как оказалось, содержит всю необходимую информацию о четырехмерном аналоге. Подобный подход позволяет значительно упростить вычисления, которые в четырехмерном пространстве представляются крайне сложными. Вместо работы с многомерными интегралами и сложными топологическими структурами, исследователи могут сосредоточиться на более простой двухмерной модели, получая те же результаты. $Z_{2d} = Z_{4d}$ Данное соответствие открывает новые возможности для изучения непертурбативных аспектов теории Янга-Миллса и способствует развитию более эффективных вычислительных методов в физике высоких энергий.

Исследования показали, что инстантоны, возникающие в рамках двухмерной теории Янга-Миллса, не просто аналогичны, но и напрямую соответствуют полюсам в четырехмерной теории. Эта связь представляет собой мощный инструмент для анализа и вычислений, поскольку позволяет переносить сложные задачи из четырехмерного пространства в более простую двухмерную модель. По сути, каждый полюс в четырехмерной теории имеет свой эквивалентный инстантон в двухмерной, что открывает новые возможности для понимания непертурбативной динамики и решения задач, которые ранее были недоступны. Такое соответствие позволяет использовать двухмерную теорию в качестве эффективного приближения для изучения свойств четырехмерной, существенно упрощая вычисления и предоставляя интуитивное представление о фундаментальных явлениях, описываемых этими теориями.

Исследования показывают, что при определенных условиях — а именно, когда число фундаментальных представлений фермионов равно двум ( $N_f = 2$ ), а число цветов равно четырем ( $N_c = 4$ ) — существует прямая связь между константой связи в двухмерной калибровочной теории и константой связи в соответствующей четырехмерной теории Янга-Милса. Эта связь выражается соотношением $g_{2d}^2 = -g_{YM}^2 / (4\pi)$ , что позволяет установить количественное соответствие между параметрами обеих теорий. Указанная взаимосвязь не только упрощает расчеты в рамках четырехмерной теории, переводя их в более доступную двухмерную форму, но и открывает новые перспективы для понимания непертурбативной динамики калибровочных полей, демонстрируя глубокую связь между различными размерностями и структурами в физике элементарных частиц.

За Пределами Возмущений: Более Широкий Математический Ландшафт

Функция Барнса G, проявляющая себя в функции разделения, представляет собой не просто математический инструмент, но и мост к более глубоким структурам специальной математики. Её появление указывает на тесную связь между, казалось бы, разрозненными областями, такими как комбинаторика, теория чисел и анализ. $G(z+1)$ представляет собой обобщение факториала, обладающее сложными свойствами, которые выходят за рамки традиционных функций. Изучение этой функции позволяет выявить скрытые симметрии и взаимосвязи в физических моделях, что особенно важно при исследовании статистической механики и квантовой теории поля. Её применение выходит далеко за рамки непосредственного вычисления интегралов, открывая путь к пониманию более фундаментальных принципов, лежащих в основе этих теорий.

Исследования показывают, что эффективный спин полей, подверженный модификации под воздействием калибровочного заряда и монопольных фонов, демонстрирует глубокую взаимосвязь между геометрией и квантовой механикой. В частности, наблюдается, что изменение спина не является просто аддитивным вкладом, а скорее сложной функцией геометрии пространства-времени и топологических свойств монополей. $S_{eff} = S_0 + f(Q, B)$ , где $S_0$ — исходный спин, $Q$ — калибровочный заряд, $B$ — монопольный фон, а $f$ — нелинейная функция, отражающая эту взаимосвязь. Данный эффект указывает на возможность возникновения новых квантовых состояний и модификаций стандартной модели частиц, поскольку спин играет ключевую роль в определении их свойств и взаимодействий. Понимание этого взаимодействия открывает новые горизонты в изучении квантовой гравитации и топологических фаз материи.

Понимание лежащей в основе данной дуальности суперконформной теории является ключевым для применения этих методов к более сложным физическим системам. Суперконформная теория предоставляет мощный математический каркас, позволяющий анализировать системы, не подверженные классическим возмущениям, и описывать их поведение в экстремальных условиях. Она оперирует симметриями, которые остаются неизменными при конформных преобразованиях и преобразованиях суперсимметрии, что позволяет строить точные решения и предсказывать свойства систем, которые в противном случае были бы недоступны для анализа. Исследование этих симметрий и их влияние на динамику физических систем, таких как $N=4$ суперсимметричная Yang-Mills теория, позволяет не только лучше понять существующие модели, но и разрабатывать новые подходы к решению задач в квантовой теории поля, гравитации и физике конденсированного состояния. Дальнейшее развитие суперконформной теории и расширение ее применимости к более реалистичным сценариям представляется перспективным направлением исследований, способным привести к прорывам в понимании фундаментальных законов природы.

Исследование демонстрирует глубокую взаимосвязь между, казалось бы, различными физическими системами — четырехмерными суперконформными калибровочными теориями и двумерной калибровочной теорией, в которой полюса в локализованном интеграле по траекториям соответствуют неустойчивым моментам. Это подтверждает представление о том, что хорошая система — живой организм, где изменение одной части неминуемо затрагивает целое. Как точно отметил Фрэнсис Бэкон: «Знание — сила». Данная работа, раскрывая взаимосвязь между 4D и 2D физикой, иллюстрирует, что истинное понимание возникает не из усложнения, а из выявления фундаментальных принципов, лежащих в основе сложных систем.

Что дальше?

Представленная работа, обнаружив связь между четырехмерными суперконформными калибровочными теориями и двухмерной физикой, обнажает фундаментальную истину: всё ломается по границам ответственности — если их не видно, скоро будет больно. Появление неустойчивых мгновенных частиц в двухмерной теории как интерпретация полюсов в локализованном интеграле — это не просто соответствие, это предупреждение. Система, в которой локальные и глобальные аспекты не согласованы, обречена на распад, и именно в этих точках несоответствия проявляются её слабости.

Очевидно, что дальнейшее исследование должно быть направлено на систематическое изучение этих границ ответственности. Необходимо расширить понимание того, как именно неустойчивые мгновенные частицы проявляют себя в различных калибровочных теориях и какие физические процессы они описывают. Особенно важно исследовать влияние квантовых эффектов и их роль в стабилизации или, наоборот, в усилении этих неустойчивостей. Структура определяет поведение, и только детальный анализ этой структуры позволит предвидеть будущие проблемы.

На горизонте маячит вопрос о возможности обобщения представленного подхода на более сложные теории, где локализация становится невозможной или не даёт ясных результатов. Возможно, именно анализ неустойчивых мгновенных частиц и их влияние на структуру теории позволит найти новые методы решения этих задач. Элегантный дизайн рождается из простоты и ясности, но для его достижения необходимо постоянно искать и устранять скрытые дефекты.

Оригинал статьи: https://arxiv.org/pdf/2602.05733.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-07 09:28