Автор: Денис Аветисян
Исследование демонстрирует, как взаимодействие между спином и кристаллической решеткой может порождать уникальные топологические свойства в материалах, открывая новые возможности для управления их механическими характеристиками.
Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.
Бесплатный телеграм-канал
В статье показано, как спин-решеточное взаимодействие индуцирует топологические механические явления в кристаллических материалах, формируя топологические решетки Максвелла с устойчивыми модами прогиба.
Несмотря на то, что топологические фазы материи обычно изучаются в контексте квантовой физики, данная работа, озаглавленная ‘Magnetopological mechanics in Maxwell lattice frustrated Mott insulators’, исследует возможность реализации топологических явлений в классических механических системах. Показано, что взаимодействие спина и решетки в фрустрированных мотт-изоляторах с решеткой Максвелла может приводить к возникновению топологических граничных мод и, как следствие, к появлению так называемой магнитотопологической механики. В частности, авторы демонстрируют, что спин-решеточное взаимодействие в кагоме-структуре индуцирует спонтанную деформацию решетки, формируя топологическую решетку Максвелла с нетривиальным спектром фононов. Может ли данный механизм открыть новые пути для управления механическими свойствами материалов и создания функциональных устройств на их основе?
В поисках прочности: от решеток к топологическим состояниям
Традиционные решетчатые модели, широко используемые в материаловедении и инженерии, зачастую оказываются недостаточно гибкими для адекватного описания сложных механических явлений. Эти модели, основанные на жестких связях и упрощенных представлениях о деформации, испытывают трудности при прогнозировании поведения материалов, подверженных значительным нагрузкам или сложным деформациям. Ограниченность их прогностической способности обусловлена неспособностью учитывать тонкие взаимодействия между элементами структуры и нелинейные эффекты, возникающие при больших деформациях. В результате, предсказания, основанные на таких моделях, могут существенно отличаться от реального поведения материалов, что снижает эффективность проектирования и разработки новых конструкций. Поэтому возникает необходимость в создании более совершенных моделей, способных адекватно описывать широкий спектр механических явлений и обеспечивать более точные прогнозы.
Максвелловские решетки представляют собой инновационный подход к конструированию материалов с заданными механическими свойствами. В отличие от традиционных решеток, обладающих либо высокой жесткостью, либо чрезмерной податливостью, эти структуры достигают уникального баланса между этими характеристиками. Это достигается за счет особого расположения и соединения элементов, позволяющего материалу эффективно рассеивать энергию и адаптироваться к внешним воздействиям. Возможность тонкой настройки жесткости и податливости открывает перспективы для создания материалов с улучшенными демпфирующими свойствами, повышенной устойчивостью к ударным нагрузкам и способностью к программируемому деформированию. Таким образом, Максвелловские решетки предоставляют инструменты для создания материалов нового поколения, способных решать сложные инженерные задачи в различных областях — от робототехники и биомедицины до авиакосмической промышленности и строительства.
В основе создания материалов с заданными механическими свойствами лежит тонкий баланс между ограничениями и степенями свободы, приводящий к состоянию, известному как изостатичность. Изостатические структуры, в отличие от жестких или податливых, демонстрируют уникальную способность распределять нагрузки, минимизируя внутренние напряжения. Этот принцип позволяет создавать материалы, способные поглощать энергию удара, изменять форму без разрушения или проявлять другие, ранее недостижимые свойства. Изостатичность не является абсолютным состоянием, а скорее точкой равновесия, где добавление или удаление связей существенно меняет механическое поведение системы. Понимание и точное управление этим балансом открывает возможности для проектирования материалов с принципиально новыми функциональными характеристиками, расширяя границы современной инженерии и материаловедения.
Топологическая механика: обуздание скрытых колебаний
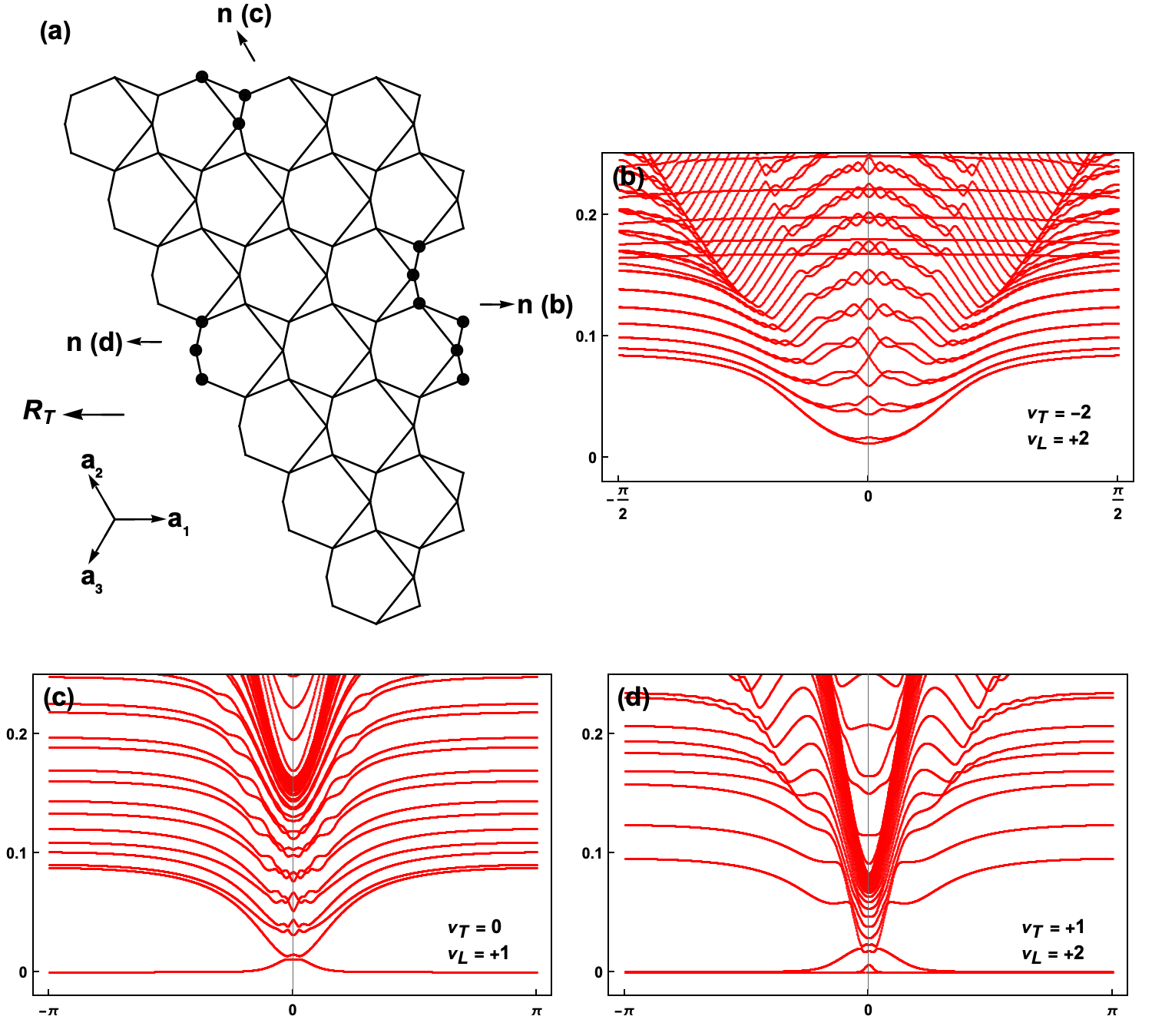
Тщательное проектирование геометрии решетки, на примере решетки Кагоме, позволяет индуцировать топологические фазы с устойчивыми механическими свойствами. Решетка Кагоме, характеризующаяся определенным расположением узлов и связей, создает специфические условия для возникновения топологических состояний. Изменение геометрии решетки напрямую влияет на спектр колебаний и распределение напряжений, позволяя контролировать механические характеристики материала. В частности, определенные конфигурации решетки приводят к появлению локализованных деформаций и устойчивости к разрушению, что обусловлено топологической защитой этих состояний от локальных возмущений и дефектов.
Топологические фазы в механических системах проявляются в виде так называемых «топологических мягких мод» (topological floppy modes) — безразрывных колебательных мод, защищенных лежащей в основе топологией. В отличие от обычных колебательных мод, которые могут иметь энергетический зазор (gap), эти моды характеризуются нулевой частотой или очень низкой частотой, что делает их устойчивыми к локальным возмущениям и деформациям структуры. Защищенность этих мод обусловлена топологическими инвариантами системы и не зависит от деталей конкретной реализации, что обеспечивает их робастность. Наличие этих безразрывных мод является прямым следствием топологических свойств материала и может быть предсказано с использованием методов топологического анализа.
Связь между топологическими свойствами среды и существованием краевых состояний описывается принципом соответствия объёма и границы (bulk-boundary correspondence). Данный принцип утверждает, что наличие топологически нетривиальных состояний в объёме материала (например, топологических «мягких» мод) напрямую обуславливает существование защищённых состояний на его границе. Эти краевые состояния характеризуются особой устойчивостью к локальным возмущениям, поскольку их существование гарантируется глобальными топологическими инвариантами материала. χ — топологический инвариант, определяющий существование этих состояний. Нарушение топологической защиты требует глобальных изменений в структуре материала, что обеспечивает исключительную надежность и устойчивость краевых состояний к дефектам и примесям.
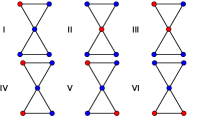
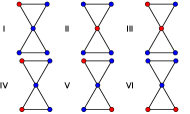
Спин-решеточное взаимодействие: магнетомеханический механизм
Взаимодействие магнитных степеней свободы с решеткой, известное как спин-решеточное взаимодействие, представляет собой эффективный механизм управления механическим поведением материалов. Данный тип взаимодействия позволяет преобразовывать магнитные воздействия в механические деформации и наоборот, открывая возможности для создания материалов с программируемыми механическими свойствами. Эффект достигается за счет изменения энергии решетки под воздействием изменения магнитных моментов, что приводит к возникновению сил, деформирующих структуру. Интенсивность этого взаимодействия зависит от конкретных материалов и геометрии структуры, а также от величины приложенного магнитного поля. Это взаимодействие отличается от традиционных методов управления механическими свойствами, таких как применение внешних сил или температурных изменений, поскольку позволяет осуществлять контроль на микроскопическом уровне, используя магнитные поля.
Для моделирования и прогнозирования результирующих механических откликов используется модель Гейзенберга и ее применение к модели Гейзенберга на решетке Кагоме. В рамках этой модели, взаимодействие между спинами атомов решетки учитывается как обменное взаимодействие, описываемое гамильтонианом Гейзенберга: H = -J \sum_{\langle i,j \rangle} \mathbf{S}_i \cdot \mathbf{S}_j, где J — константа обменного взаимодействия, а суммирование производится по всем парам ближайших соседей. Применение этой модели к решетке Кагоме позволяет рассчитать зависимости между магнитными моментами и возникающими деформациями, а также предсказать критические значения внешних воздействий, приводящие к изменению механических свойств материала. Решетка Кагоме, характеризующаяся специфической геометрией, демонстрирует уникальные магнитные и механические свойства, обусловленные особенностями спин-решеточного взаимодействия.
Взаимодействие спина с кристаллической решеткой приводит к возникновению внутренних самонапряжений в решетке, что оказывает существенное влияние на возникающие топологические гибкие моды и их стабильность. Критическое значение параметра спин-решеточной связи, равное b > 1/6, является необходимым условием для формирования топологической решетки Максвелла. Превышение этого порога приводит к изменению механических свойств материала и формированию особых топологических состояний, характеризующихся специфическими колебательными модами и устойчивостью к деформациям.
Вычислительная проверка и спектральные сигнатуры
С использованием вычислительных методов, таких как ‘Simulated Annealing’ (имитация отжига), стало возможным определение состояний с наименьшей энергией для этих сложных систем. Данный подход позволяет не только идентифицировать фундаментальное состояние, но и подтвердить существование топологических ‘мягких’ мод — особых колебаний решетки, обусловленных топологическими свойствами материала. Имитация отжига, благодаря своей способности преодолевать энергетические барьеры, эффективно исследует пространство возможных конфигураций, выявляя стабильные структуры и подтверждая теоретические предсказания о наличии этих уникальных мод, что открывает перспективы для управления свойствами материалов на основе их топологической структуры.
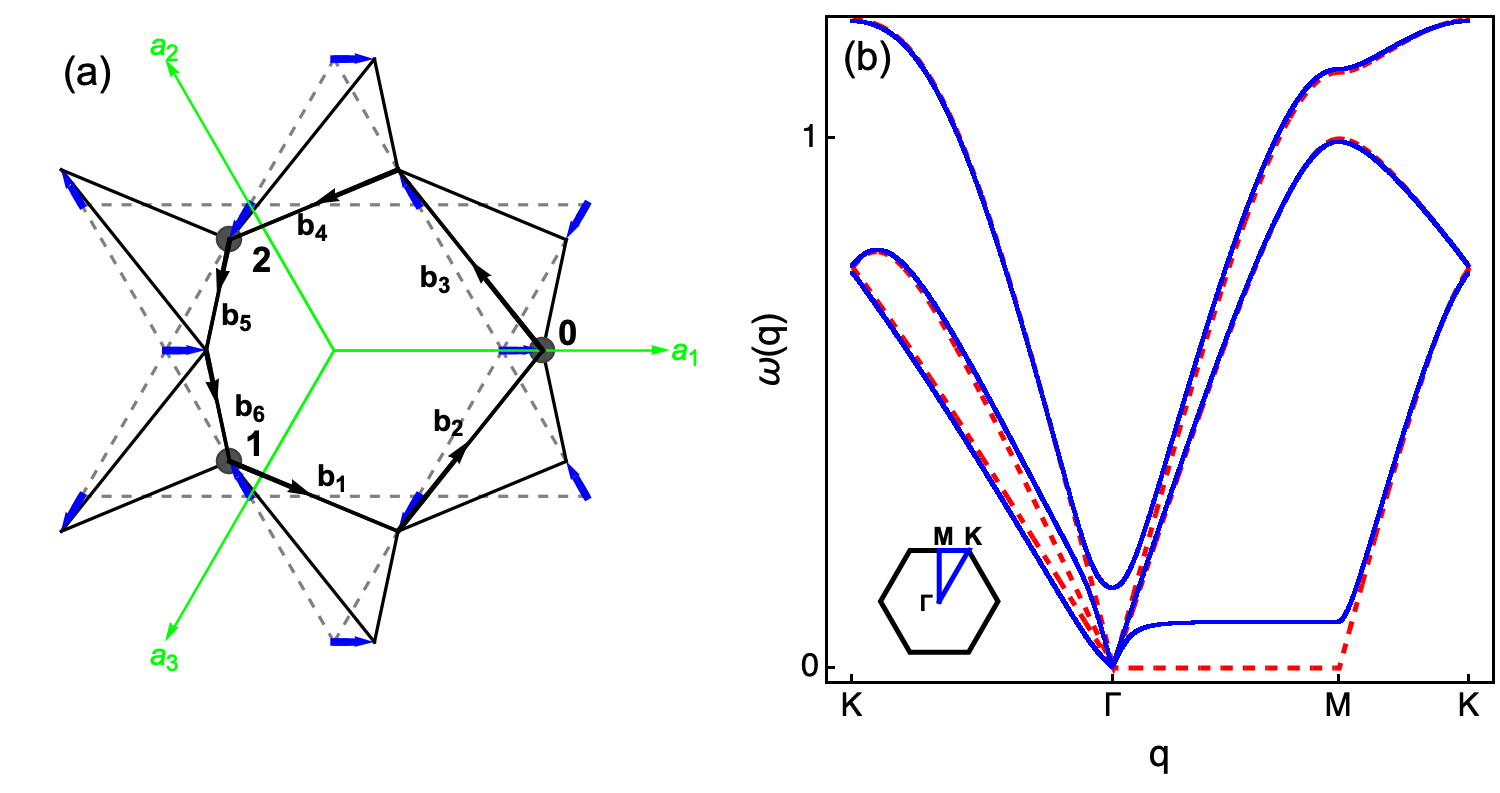
Анализ фононного спектра предоставляет непосредственное подтверждение существования топологических «мягких» мод. В частности, выявление zero modes — состояний с нулевой частотой — является ключевым признаком этих мод. Эти особые состояния возникают в определенных точках спектра и свидетельствуют о наличии степеней свободы, связанных с топологическими свойствами кристаллической решетки. Обнаружение и характеристика этих zero modes позволяет не только подтвердить теоретические предсказания о существовании «мягких» мод, но и понять их вклад в динамические и структурные свойства материала, а также связать их с топологической поляризацией и особенностями фазовых переходов.
В фазе плато 1/9, наблюдаемое искажение кристаллической решетки приводит к значительному увеличению размера элементарной ячейки — до 27 узлов и 54 связей. Это структурное изменение оказывает существенное влияние на топологические свойства системы: измеренная величина топологической поляризации R_T равна нулю. Данный результат указывает на то, что в данной фазе наблюдаются исключительно локальные, граничные «мягкие» моды, а не протяженные топологические состояния, характерные для других фаз. Таким образом, изменение размера ячейки напрямую коррелирует с природой наблюдаемых колебаний решетки и их топологическим поведением, что позволяет более детально характеризовать свойства материала.
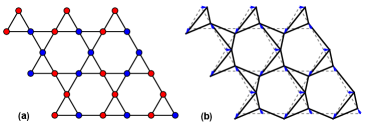
Расширение горизонтов: к многомерным архитектурам
Решетка Кагоме, являясь убедительной моделью для изучения топологической механики, не является предельным случаем. Ученые активно исследуют возможность переноса принципов, лежащих в основе этой механики, на более сложные трехмерные структуры, в частности, на решетку Пирохлора. Эта решетка, характеризующаяся особой геометрией и соединениями, открывает новые возможности для создания материалов с уникальными свойствами. В отличие от двухмерных систем, трехмерные решетки, такие как Пирохлора, позволяют реализовать более сложные топологические состояния и защищенные от дефектов граничные состояния, что потенциально ведет к разработке материалов с повышенной механической устойчивостью и неординарными функциональными характеристиками. Исследования в этом направлении позволяют расширить границы применимости топологической механики и создать принципиально новые типы материалов.
Сочетание топологических свойств, магнетизма и геометрии кристаллической решетки открывает возможности для создания материалов с беспрецедентной механической устойчивостью и функциональностью. Исследования демонстрируют, что манипулирование этими взаимосвязанными параметрами позволяет конструировать структуры, способные эффективно рассеивать энергию и противостоять деформациям. Например, особые конфигурации спиновых состояний в решетках типа пирохлора могут приводить к возникновению топологически защищенных состояний, обеспечивающих высокую устойчивость к внешним воздействиям. Такой подход позволяет не только создавать более прочные материалы, но и наделять их уникальными свойствами, такими как контролируемая проводимость, способность к самовосстановлению или повышенная эффективность преобразования энергии, что открывает перспективы для инноваций в различных областях — от аэрокосмической промышленности до биомедицинских имплантатов.
Эффективный спин-гамильтониан представляет собой фундаментальную основу для анализа и прогнозирования поведения сложных систем, особенно в контексте топологической механики и материаловедения. Этот математический инструмент позволяет упростить описание взаимодействий между элементами системы — будь то спины в магнитных материалах или механические степени свободы в метаматериалах — и выявить ключевые параметры, определяющие их коллективное поведение. Благодаря спин-гамильтониану становится возможным моделирование и предсказание различных фаз и переходов в материалах, включая топологические фазы, характеризующиеся устойчивостью к дефектам и необычными свойствами. Разработка и оптимизация материалов с заданными характеристиками, таких как повышенная механическая прочность или уникальные магнитные свойства, основывается на точном определении и управлении параметрами, входящими в этот гамильтониан, открывая новые горизонты в области материаловедения и инженерии.
Исследование демонстрирует, как взаимодействие спина и кристаллической решетки порождает нетривиальные топологические состояния в материалах. Авторы, по сути, конструируют топологические «максвелловские решетки» с устойчивыми «мягкими модами». Это напоминает старую истину: любая элегантная теория рано или поздно встретится с жестокой реальностью. Как точно подметил Джон Локк: «Ум — это не врожденная способность, а способность приобретать». В данном случае, материал «приобретает» топологические свойства благодаря сложному взаимодействию, а не благодаря изначально заложенной программе. И, как обычно, практика показывает, что даже самые красивые математические модели нуждаются в проверке на прочность — в данном случае, в физической реализации и экспериментальной проверке этих самых «мягких мод».
Куда же мы катимся?
Представленная работа, безусловно, добавляет ещё один слой сложности в и без того запутанную картину топологических фаз материи. Концепция «магнитотопологической механики» звучит неплохо в аннотации, но не стоит забывать, что любая «устойчивая» топологическая особенность — это лишь вопрос времени до того, как найдётся способ её разрушить внешним возмущением или, что вероятнее, ошибкой в скрипте автоматической сборки. Эти самые «робастные» моды оказываются удивительно чувствительны к малейшим отклонениям параметров кристаллической решетки, которые в реальных материалах неизбежны.
Более того, реальные материалы не любят идеальных моделей. Кагоме-решетка, конечно, красива на бумаге, но в производстве всегда найдётся дефект, который превратит элегантную топологию в хаотичную мешанину спинов. Изучение влияния случайных примесей и дефектов на эти «мягкие» моды представляется задачей нетривиальной, и, вероятно, потребует привлечения специалистов по статистической физике и, возможно, даже шаманов.
В конечном счёте, данное исследование — это ещё один кирпичик в фундаменте, который, возможно, когда-нибудь станет небоскрёбом. Но, как показывает практика, чаще всего этот фундамент оказывается заброшенным, а на его месте вырастает парковка. Поэтому, прежде чем говорить о практическом применении «магнитотопологической механики», стоит убедиться, что её можно воспроизвести хотя бы в десяти образцах подряд.
Оригинал статьи: https://arxiv.org/pdf/2602.12168.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Решение головоломки с паролем Absolum в Yeldrim.
- Прогнозы криптовалюты AXS: информация о ценах на AXS
- Откровенные заметки, слитые стримером Lacari, привели к его бану на Twitch и Kick.
- Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip
- The Planet Crafter: полное руководство по картам и биомам
- YAPYAP Список заклинаний
- 15 лучших законченных серий манхвы, которые стоит прочитать, в рейтинге
- Все рецепты культистского круга в Escape from Tarkov
- Где находится точка эвакуации «Туннель контрабандистов» на локации «Интерчейндж» в Escape from Tarkov?
- The Division 2 Y7S3 Scout 2 Manhunt Riddle Solutions
2026-02-15 09:17