Тень материи: как окружение влияет на вращающиеся черные дыры

Автор: Денис Аветисян

Новое исследование показывает, как темная материя, окружающая черную дыру, искажает пространство-время вокруг нее, изменяя траектории орбит и сигналы гравитационных волн.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал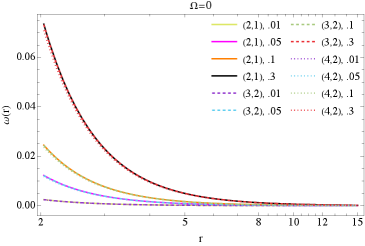

Радиальный профиль угловой скорости увлечения, вызванного вращающимся телом в пространстве-времени, окружённом гало из тёмной материи, демонстрирует отклонение от поведения в вакууме, обусловленное влиянием гало, моделируемого как анизотропное вещество с плотностью по типу Эрнквиста, причём конфигурация гало, определяемая параметрами <span class="katex-eq" data-katex-display="false">Loga\_0</span> и <span class="katex-eq" data-katex-display="false">LogM\_{\rm Halo}</span>, оказывает заметное воздействие на инерционное увлечение. — Радиальный профиль угловой скорости увлечения, вызванного вращающимся телом в пространстве-времени, окружённом гало из тёмной материи, демонстрирует отклонение от поведения в вакууме, обусловленное влиянием гало, моделируемого как анизотропное вещество с плотностью по типу Эрнквиста, причём конфигурация гало, определяемая параметрами $Loga\_0$ и $LogM\_{\rm Halo}$ , оказывает заметное воздействие на инерционное увлечение.

В статье исследуются геометрические свойства медленно вращающихся черных дыр, погруженных в среду, содержащую гало из темной материи, и их влияние на частоты эпициклических орбит.

Известно, что астрофизические черные дыры не существуют в вакууме, а окружены темной и барионной материей, влияющей на геометрию пространства-времени. В работе ‘Geometric properties of slowly rotating black holes embedded in matter environments’ исследуются геометрические свойства медленно вращающейся черной дыры, погруженной в окружение, моделируемое анизотропной жидкостью, представляющей гало темной материи. Показано, что присутствие и вращение гало приводят к заметным отклонениям от геометрии черной дыры в вакууме, модифицируя эффекты увлечения инерциальных систем отсчета, геодезические круговые орбиты и характеристики светового кольца. Как эти изменения могут проявиться в гравитационных волнах от экстремальных спиралей и стать ключом к проверке общей теории относительности в сильных гравитационных полях?

Ткань Пространства-Времени: Вакуумные Решения и Тёмная Материя

Для точного описания Вселенной необходимы детальные модели пространства-времени, отправной точкой в построении которых служат идеализированные решения уравнений гравитации для вакуума, такие как метрики Шварцшильда и Керра. Метрика Шварцшильда, описывающая геометрию вокруг невращающейся сферически симметричной массы, представляет собой простейший пример, позволяющий исследовать гравитационное поле чёрной дыры. Более сложная метрика Керра учитывает вращение центрального объекта, что существенно влияет на структуру пространства-времени вблизи него и предсказывает существование эргосферы — области, из которой энергия может быть извлечена. Эти решения, хотя и упрощены, являются фундаментальными для понимания гравитационных явлений и служат основой для построения более реалистичных моделей, учитывающих влияние материи и энергии на геометрию Вселенной. Изучение этих вакуумных решений позволяет ученым глубже проникнуть в природу гравитации и понять структуру пространства-времени в экстремальных условиях.

Фундаментальные решения уравнений гравитации, описывающие вакуумные пространства-времена вокруг черных дыр, такие как метрики Шварцшильда и Керра, редко встречаются изолированно во Вселенной. Напротив, они обычно погружены в сложные гравитационные среды, в частности, окружены гало из темной материи. Эти гало оказывают существенное влияние на динамику пространства-времени, изменяя геометрию и траектории движения объектов. Темная материя, составляющая большую часть массы галактик, формирует протяженные гало, которые искривляют пространство-время вокруг черных дыр, приводя к отклонениям от предсказаний, основанных на чистых вакуумных решениях. Изучение взаимодействия между черными дырами и темной материей имеет решающее значение для построения реалистичных моделей галактик и понимания процессов, происходящих в экстремальных гравитационных условиях.

Для создания адекватных моделей галактических сред необходимо учитывать распределение темной материи, поскольку она оказывает существенное влияние на гравитационную динамику. Вместо упрощенных представлений, ученые часто используют профили, такие как профиль Эрнквиста, для описания распределения темной материи в галактических гало. Этот профиль характеризуется более высокой концентрацией темной материи в центре и более плавным спадом к периферии, что лучше соответствует наблюдаемым вращательным кривым галактик. Использование профиля Эрнквиста позволяет более точно моделировать гравитационное поле, окружающее галактики, и, следовательно, получать более реалистичные результаты в исследованиях динамики звезд, движения газа и формирования структур в галактических средах. Понимание распределения темной материи — ключевой элемент в построении всеобъемлющей картины эволюции галактик и Вселенной в целом.

Отклонение сохраненной энергии от вакуумного значения для круговых орбит в медленно вращающемся пространстве-времени, окруженном гало из темной материи, демонстрирует различия между проградными и ретроградными орбитами и зависит от параметров гало, что обусловлено инерциальным увлечением и гравитационным влиянием анизотропного распределения темной материи, смоделированного профилем Хернквиста.

Траектории в Искривленном Пространстве: Геодезическое Движение и Орбитальная Динамика

Расчет движения пробных частиц, описываемый геодезической динамикой, является фундаментальным для понимания физических процессов вблизи черных дыр и внутри галактик. Геодезические представляют собой пути, по которым движутся частицы в искривленном пространстве-времени, и их вычисление позволяет моделировать траектории объектов, не подверженных внешним силам, кроме гравитации. Анализ геодезических позволяет исследовать такие явления, как гравитационное линзирование, прецессия перигелия орбит, а также поведение материи в аккреционных дисках. Точность определения геодезических напрямую влияет на интерпретацию наблюдательных данных и построение моделей гравитационных систем, включая изучение распределения темной материи и проверку общей теории относительности в сильных гравитационных полях. $\frac{d^2x^\mu}{d\tau^2} + \Gamma^\mu_{\alpha\beta} \frac{dx^\alpha}{d\tau} \frac{dx^\beta}{d\tau} = 0$ — это уравнение геодезической, где $\Gamma^\mu_{\alpha\beta}$ — символы Кристоффеля, определяющие геометрию пространства-времени.

Формализм Гамильтона-Якоби представляет собой мощный аналитический метод решения уравнений движения, описывающих траектории тестовых частиц в гравитационных полях. В отличие от прямого численного интегрирования уравнений Эйлера, данный подход использует функцию Гамильтона-Якоби $S(q,t)$ , позволяющую свести задачу о движении к решению одного частного уравнения в гамильтоновом формализме. Это особенно полезно при анализе сложных систем, таких как движение вокруг чёрных дыр или в галактиках, где необходимо учитывать эффекты релятивистской гравитации и нелинейные взаимодействия. Решение уравнения Гамильтона-Якоби позволяет получить константы движения и определить орбитальные параметры, такие как эксцентриситет и большая полуось, обеспечивая точные предсказания поведения орбит.

Расчеты траекторий движения тел позволяют определить ключевые орбитальные характеристики, такие как внутреннее стабильное круговое орбитальное расстояние (Innermost Stable Circular Orbit, ISCO) и эпициклическую частоту. ISCO определяет минимальное расстояние, на котором может существовать стабильная круговая орбита, а эпициклическая частота характеризует частоту малых колебаний вокруг этой орбиты. Данное исследование количественно оценивает изменение этих параметров под влиянием гало темной материи. Установлено, что наличие гало темной материи приводит к модификации ISCO и эпициклической частоты, влияя на стабильность орбит и, следовательно, на динамику движения объектов в гравитационном поле. Величина изменения параметров зависит от концентрации и профиля распределения темной материи, что позволяет использовать эти характеристики для изучения свойств гало темной материи. $\omega_{ep} = \sqrt{\frac{GM}{r^3}}$ — пример формулы для расчета эпициклической частоты.

Приближение медленного вращения (slow rotation approximation) значительно упрощает расчеты траекторий движения в сильных гравитационных полях, особенно при изучении эффекта увлечения пространства-временем (frame dragging). В рамках этого приближения, угловая скорость вращающегося объекта считается значительно меньшей, чем его орбитальная скорость. Это позволяет пренебречь некоторыми членами в уравнениях движения, что существенно снижает вычислительную сложность. В частности, при анализе движения пробных частиц вокруг вращающейся черной дыры, приближение медленного вращения позволяет эффективно рассчитать метрику Керра и, как следствие, определить характеристики орбит, такие как внутреннее стабильное круговое орбитальное движение (ISCO) и эпициклическая частота, с приемлемой точностью. Данное приближение особенно полезно при моделировании динамики аккреционных дисков и изучения влияния вращения центрального объекта на их структуру и эволюцию.

Различие в угловом моменте для круговых орбит в медленно вращающемся пространстве-времени, окруженном гало из темной материи, по сравнению с вакуумом, демонстрирует радиальную зависимость и асимметрию между прямыми и обратными орбитами, обусловленные гравитацией гало и инерционным увлечением, вызванным анизотропным распределением темной материи типа Эрнквиста.

Спирали с Большим Соотношением Масс: Источник Гравитационных Волн

Экстремальные спирали с большим соотношением масс (EMRI) возникают, когда компактный объект, масса которого значительно меньше массы сверхмассивной черной дыры (обычно от $10^{-6}$ до $10^{-2}$ солнечных масс), входит в сильное гравитационное поле черной дыры и постепенно спирально сближается с ней. В процессе этого сближения объект излучает гравитационные волны, амплитуда и частота которых меняются по мере уменьшения расстояния между объектами. Интенсивность излучаемых гравитационных волн пропорциональна квадрату ускорения объекта, что делает EMRI одним из наиболее мощных источников гравитационного излучения, доступных для обнаружения современными и будущими гравитационно-волновыми обсерваториями. Эти сигналы содержат информацию о параметрах системы, включая массы объектов и характеристики пространства-времени вокруг черной дыры.

Сигналы, генерируемые спиралями экстремальных массовых соотношений (EMRI), несут в себе информацию о различных характеристиках сверхмассивной черной дыры и геометрии окружающего ее пространства-времени. Анализ этих сигналов позволяет определить массу и спин черной дыры, а также параметры ее окружения, включая наличие и распределение темной материи. Форма сигнала, в частности частота и амплитуда, кодирует информацию о траектории малого объекта при спирали, что позволяет реконструировать структуру пространства-времени вблизи черной дыры и проверить предсказания общей теории относительности. Изменения в форме сигнала, вызванные, например, отклонениями от метрики Шварцшильда, могут указывать на наличие дополнительных эффектов, таких как вращение черной дыры или влияние темной материи на геометрию пространства-времени. $f = \frac{1}{2\pi R^3}\sqrt{\frac{GM}{R^3}}$ , где f — частота сигнала, G — гравитационная постоянная, M — масса черной дыры, а R — радиус орбиты.

Для регистрации и анализа гравитационных волн, генерируемых экстремальными спиралями массивных объектов, требуются высокочувствительные гравитационно-волновые обсерватории. В настоящее время перспективными являются космические миссии LISA (Laser Interferometer Space Antenna) и TianQin. LISA представляет собой триангулярную сеть из трех космических аппаратов, расположенных на орбите Солнца, что позволяет регистрировать низкочастотные гравитационные волны, недоступные для наземных детекторов. Миссия TianQin, разрабатываемая Китаем, также использует три космических аппарата для регистрации гравитационных волн в аналогичном частотном диапазоне. Высокая точность измерения, обеспечиваемая этими миссиями, критически важна для обнаружения слабых сигналов от экстремальных спиралей и извлечения информации о свойствах сверхмассивных черных дыр и окружающей их темной материи.

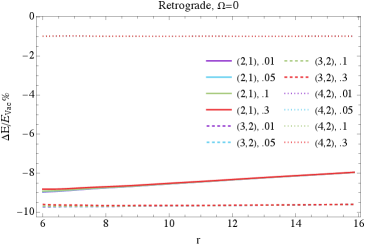
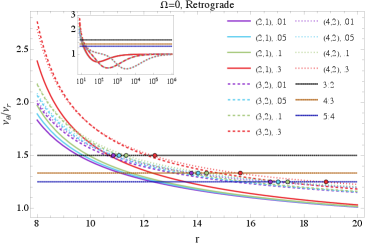
Точность волновых моделей, получаемых на основе расчетов геодезических движений, является критически важной для успешного обнаружения и оценки параметров экстремальных спиралей малого и большого соотношения масс (EMRI). Представленное исследование демонстрирует систематические сдвиги в радиальном положении эпициклических резонансов, оказывающих влияние на сигналы гравитационных волн. В частности, были количественно оценены изменения внутренней стабильной круговой орбиты (ISCO) и частот эпициклических движений, вызванные наличием гало из темной материи. Эти модификации необходимо учитывать при построении точных волновых моделей и анализе данных, получаемых от будущих гравитационно-волновых обсерваторий, таких как LISA и TianQin, для корректной интерпретации наблюдаемых сигналов и получения информации о свойствах сверхмассивных черных дыр и окружающей их темной материи.

Отношение вертикальной и радиальной эпициклических частот, зависящее от радиуса, демонстрирует асимметрию между проградными и ретроградными орбитами и отклонения от поведения в вакууме, вызванные увлечением инерциальных систем отсчета, модифицированным гало темной материи, при различных конфигурациях плотности и значениях χ.

Исследование геометрии пространства-времени вокруг медленно вращающихся чёрных дыр, окружённых гало из тёмной материи, неизбежно напоминает о вечной борьбе теории и практики. Авторы пытаются описать влияние окружающей среды на орбитальную динамику, что, в конечном итоге, может повлиять на сигналы гравитационных волн. Как будто пытаются предсказать поведение системы, зная, что «продакшен» — в данном случае, сама Вселенная — всегда найдёт способ внести свои коррективы. В этом контексте особенно уместны слова Конфуция: «学习之不厌，诲人不倦» (xuéxí zhī bù yàn, huì rén bù juàn) — «Не уставай учиться, не уставай обучать». Ибо познание геометрии чёрных дыр — процесс бесконечный, а любые модели — лишь приближение к реальности, которое требует постоянной проверки и корректировки.

Что дальше?

Представленная работа, как и большинство подобных, выявляет очередные нюансы влияния окружения на геометрию пространства-времени вокруг чёрных дыр. Однако, стоит признать: каждая «элегантная» модель, учитывающая гало из тёмной материи, лишь откладывает неизбежное столкновение с реальностью. Продакшен, в лице гравитационных волн от экстремальных систем, рано или поздно покажет, где теория треснула по швам. Впрочем, это и есть суть прогресса: сначала идеализация, потом — отладка.

Очевидным направлением дальнейших исследований представляется не столько усложнение моделей, сколько разработка более адекватных методов верификации. Если баг воспроизводится — значит, у нас стабильная система. Иными словами, необходимо сосредоточиться на создании тестовых сценариев, способных выявить отклонения от предсказаний даже в самых «гладких» моделях. Обещания о самовосстановлении — это всегда признак того, что что-то ещё не сломалось.

В конечном счёте, документация по всем этим гало и эпициклическим частотам — это, скорее, форма коллективного самообмана. Но пусть так. Главное, чтобы в следующий раз, когда придётся сталкиваться с несовпадением теории и практики, было ясно, где именно возникла проблема. И не стоит забывать: каждая «революционная» технология завтра станет техдолгом.

Оригинал статьи: https://arxiv.org/pdf/2602.10579.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-12 19:01